2. 高速水动力航空科技重点实验室, 湖北 荆门 448035
2. Key Aviation Scientific and Technological Laboratory of High-Speed Hydrodynamic, Jingmen 448035 China
潜艇的快速性[1]是评价潜艇综合航行性能的一项重要战术技术指标,预报实艇阻力通常通过水池模型试验进行,无论是从模型的设计安装还是测量仪器的要求上,水下航行体的阻力试验都要困难和复杂许多,一方面,在考虑水池大小的情况下要保证模型有足够大小,一般要求潜艇模型在 4~5 m 之间,以达到所要求的临界雷诺数[2],由于完全浸深在水下,模型的强度要求也较高,另一方面艇模采用何种方式与拖车连接才能最大限度排除干扰也是一个重要的影响因素。目前国内外采用过的水下快速性能试验系统有 2 种:深浸深单支架系统,其浸深比达到1,不考虑模型的Fn大小,由于试验水深的限制和结构强度振动问题,该系统应用较少,另一种是浅浸深高速或低速双支架系统,这种情况主要考虑按傅氏数避开兴波干扰的峰值点,低速情况下的极端情况就是水面试验,当傅氏数足够小时就可认为无兴波干扰,但由于低速时雷诺数小,测力也小,精确性得不到很好的保证,故一般浅浸深高速系统应用较多。美国泰勒水池[3](NSRDC)很早就进行了相关研究,为尽可能消除自由表面兴波影响,其将模型潜深置于一个模型长度,采用单剑来连接拖车和模型。
本文采用浅浸深系统,通过开展 4 种不同剑型与连接方式的裸艇模阻力试验,将其结果与 ITTC 公布的试验数据进行对比,研究不同剑型与连接方式对试验结果的影响。在此基础上,选取状态三采用 CFD 方法对其阻力进行数值仿真,分析连接剑对艇体表面压力分布及其周围流场的影响。
1 主要仪器设备高速拖曳试验水池及其配套的拖车等高速水动力试验设备技术指标如下:
水池主尺度:池长 510 m,池宽 6.5 m,池深 6.8 m,水深 5.0 m。
拖车性能:速度范围 0.1~22 m/s,车速稳定精度优于 0.2%。
测试手段:试验数据采集和处理分析自动化。
水下试验专用电测阻力仪,共 2 只,单传感器量程 200 kg,采样频率 100 Hz。该传感器作为测量水下阻力的关键设备,主要特点如下:
1)至少能承受艇模重量的垂向力,以满足安装要求,并且保证长时间浸泡性能也足够稳定。
2)在水平纵向力的作用下具有良好的动态响应,可精确进行艇模水下阻力测量,同时具有很大刚度和强度,在可能遇到的侧向力作用下变形小,不会对水平纵向力测量产生干扰。
3)具有可靠纵向限位机构,整个系统即在超量程的水阻力或者惯性力下能自动保护。
2 试验模型 2.1 模型的设计试验模型依据 ITTC 公布的 Suboff 标模线型进行加工设计,模型缩尺比 1:10,主尺度如表 1 所示:
|
|
表 1 标模主要几何参数 Tab.1 Main parameters of Suboff |
模型采用内部钢骨架加外敷玻璃钢的结构形式,用于试验安装和承力的钢骨架能保证艇模具有足够的强度,外敷玻璃钢保证模型的外形光顺和不变形,油漆表面光滑,满足相关规范要求[4]。

|
图 1 高速拖曳水池 Fig. 1 The high speed towing tank |
试验模型采用双剑方式与拖车进行连接,为尽可能减小表面兴波影响,一般要求浸深比大于 0.28[4],同时应考虑模型与池底距离以减小浅水效应,最终使得模型处于无纵倾、无偏转状态,位于水池中心且与轨道中心线平行。

|
图 2 Suboff 数模 Fig. 2 Numerical model of Suboff |

|
图 3 模型试验安装 Fig. 3 Experimental installation of model |
试验过程需要注意如下几点:
1)阻力仪的标定:前后剑各安装一个水下阻力仪,直接测量艇体所受阻力,试验前首先在平台上对单个水下阻力仪进行标定,然后再对双阻力仪系统进行标定,保证双阻力仪系统技术指标满足试验要求,如图 4 所示。

|
图 4 双阻力仪标定 Fig. 4 Calibration of resistance test instrument |
2)模型完全入水后将产生 300 kg 左右的浮力,为减小负浮力对拖曳剑的影响,在模型内部填充泡沫以增加浮力,重心位置低于浮心且位于双剑中间。
3)拖曳双剑与拖车螃蟹架连接,安装时调整好前后航向误差,再将模型吊装至船坞与双剑连接。安装完成后,利用模型的水平基准线与高度尺对模型姿态进行微调,保证模型安装首尾航向误差不大于 2 mm,模型首尾高度误差不大于 2 mm,确保模型姿态不影响试验结果的真实性。
4)测试系统的标定:安装完成后,利用滑轮、钢索及数显电子称对整个测试系统进行标定,确保测试系统的准确性。
2.3 连接状态为了研究不同的剑型与连接方式对裸艇模阻力结果的影响,进行如下 4 种状态的阻力试验,拖曳速度分别为:3.045,4,5.144,6.09,7.16,8.23,9.254 m/s;
1)双剑长度 2 000 mm,上半部分为栅格状,下半部位为流线型,阻力仪直接连接于剑端和模型之间。
2)双剑长度 2 000 mm,整体均为流线型,阻力仪直接连接于剑端和模型之间。
3)考虑消除双剑安装过程中相互作用内力可能对试验结果造成的影响,在状态 2 基础上将后剑与水下阻力仪之间加一段线性滑轨再与模型相连。
4)为验证状态 3 的可行性与可靠性,将前后连接方式调换,即线性滑轨安装到前剑与阻力仪之间。
3 试验结果依据 CB/Z 216-2008 “潜艇模型阻力、自航试验方法”[4]进行试验数据处理,得到不同雷诺数下模型的总阻力系数、摩擦阻力系数,进而得到形状阻力系数。相关公式如下:
雷诺数Rn可根据下式确定:
| $ Rn{\rm{ = }}V \times L{\rm{ /}}\upsilon {\rm{;}} $ | (1) |
总阻力系数CM:
| $ {C_M}{\rm{ = }}{R_M}{\rm{ /}}{R_M}(0.5 \times \rho \times {V^2} \times S); $ | (2) |
摩擦阻力系数Cf按 ITTC 公式计算:
| $ {C_f}{\rm{ = }}0.075/0.075{(\log Rn - 2)^2}; $ | (3) |
形状阻力系数Cr:
| $ {C_r}{\rm{ = }}{C_M} - {C_f}\text{。} $ | (4) |
各个状态下的试验结果如表 2 所示。
|
|
表 2 阻力试验结果 Tab.2 Resistance experimental results |
由表 2 可知,状态 1 阻力试验数据 6.09 m/s 之前大于 ITTC 公布值,速度大于 7.16 m/s 后,阻力值反而较 ITTC 值偏小,速度越高,偏差也越大,状态 2 在 3.045 m/s 和 7.16 m/s 时与 ITTC 值非常接近,误差不到 2%,但在高速时与 ITTC 值相差较大。状态 1 和状态 2 阻力数据的变化规律明显不同,说明剑的形式对测试结果有一定影响。整体来看,状态 3 与状态 4 的阻力试验数据非常接近且变化规律一致,说明线性滑轨无论是在前剑还是后剑都具有较高可靠性,在速度 6.5 m/s 之前和 9 m/s 之后,阻力试验数据大于 ITTC 值,在速度 6.5~9 m/s 范围内,阻力试验数据非常接近 ITTC 值。由于状态 3 和状态 4 相对于状态 2 只是在阻力仪和剑之间安装形式不同,从试验结果来看,低速下较状态 2 阻力有所增加,速度大于 7.16 m/s 时,阻力值明显减小,可能是高速下线性滑轨的存在有效地消除了前后剑之间的结构内应力。
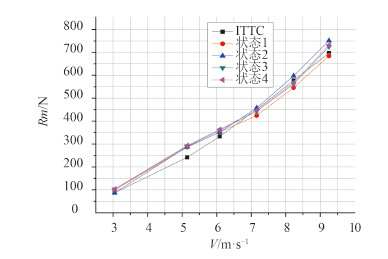
为从比较试验中各项阻力系数成份的变化,选取状态 3 计算出各项阻力系数,并在图 5 中绘出了总阻力系数、摩擦阻力系数,形状阻力系数随速度变化曲线。
|
图 5 各个速度下阻力试验结果 Fig. 5 Resistance experimental results at different velocity |
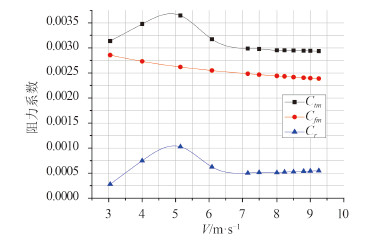
由图 6 分析可得:
|
图 6 各项阻力系数的变化曲线 Fig. 6 Resistance coefficient curves |
1)测试结果有较好重复性,数据规律性较好,无异常离散情况,说明测试结果具有一定的准确可靠度。
2)当傅汝德数大于 1.2 时,剩余阻力系数曲线已趋于平滑,兴波阻力系数Cw为 0,由此可以求出艇模形状阻力系数Ce= 0.532 × 10-3。
3)剩余阻力系数曲线在傅汝德数为 0.8 附近出现一个十分突出的峰区,按理此时兴波阻力系数应该逐渐减小,分析研究此时恰与水深付汝德数$ {F_w} = V/\sqrt {gh} {\rm{ = }}1 $ 一致,说明有一定的浅水波的影响。
4)本次试验结果直接由电测阻力仪直接测出,不包含剑阻力在内,所以未作任何修正。
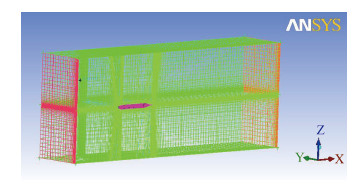
4 数值分析作为试验结果的补充,针对状态 3 采用 CFD 方法研究剑对艇流场分布的影响,将艇模置于一个与模型中心同轴线的圆柱形流场区域中,进口面距艇首 1 倍艇长,出流面距艇尾 2.5 倍艇长,网格划分采用结构化网格,在靠近潜艇表面的边界层区域进行加密处理,边界层第 1 层网格厚度为 0.6 mm,网格增长率为1.2,总网格数为 250 万,网格划分如图 7 和图 8 所示。
|
图 7 计算流域网格划分 Fig. 7 Meshing of flow field |
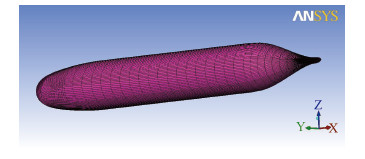
|
图 8 艇表面网格划分 Fig. 8 Meshing of model surface |
采用 RNGk-s湍流模型[5]求解 Reynolds 平均 N-S 方程[5],自由液面捕捉采用 VOF[6] 方法,入口及外边界设置为速度入口[7],出口认为流动在该处已充分发展,设置为压力出口,艇体表面设置为无滑移壁面条件[8]。
计算结果如表 3 所示。
|
|
表 3 状态 3 数值计算结果 Tab.3 Numerical calculation results of test 3 |
由表 3 可知,计算值比试验值偏大,总体误差在 4% 以内,具有较好一致性,说明试验测试结果还是可信的。图 9 为艇体流场在不同速度时的直观显示。
|
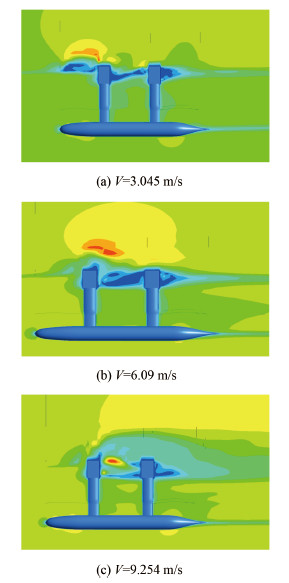
图 9 流场流速分布 Fig. 9 Velocity distribution of flow field |
试验剑对于空气流场影响区域,随着速度的增加逐步后移,直至移动到 2 个试验件之间。同时,试验剑对于水流场的影响区域,先随着速度的增加逐步下移,再由于速度的增加向后移动,而逐步上升,离开艇体。由伯努力定律可知,速度的变化必然导致压力的变化,图 10 为连接剑及艇体表面压力云图。
|
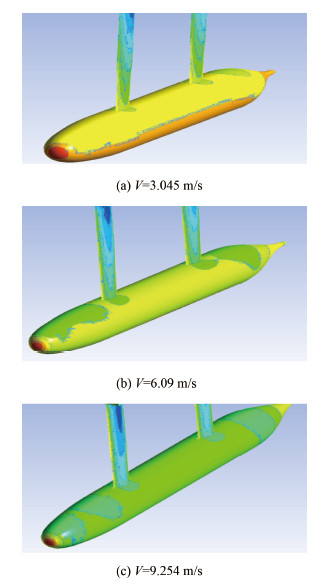
图 10 艇体及试验剑压力分布 Fig. 10 Pressure distribution of submarine and sword surface |
在艇体背部可看出,随着速度的增加,试验剑对艇体表面压力的影响区域也随之增加,并且后剑增加幅度较大。试验剑的存在给艇体表面带来非正常的压降,对于试验测试结果会产生不利影响。
5 结 语1)剑的形式以及剑与艇体的安装连接方式都会对试验结果产生明显影响,整体来看,流线型剑体以及加装线性滑轨的连接方式所得试验结果较为可靠。
2)在当前的浸深下分析所得剩余阻力系数在付汝德数为 0.8 左右出现明显峰值,此时水深付汝德数恰为 1,说明有一定的浅水波影响。
3)数值计算结果与试验结果误差在 4% 以内,说明试验所得结果还较为可靠,速度云图及压力云图的分析表明试验剑的存在给艇体表面带来非正常压降,并且速度越大,影响区域也逐步增加。
4)本次试验能够为潜器水下试验积累宝贵经验,在此基础上,拟后期开展浅水波影响研究,并且进一步改善剑体连接位置,以期探索更适合潜艇水下试验的水池拖曳方法。
| [1] |
应良镁, 沈泓萃. 潜艇快速性模型试验分析及实艇预报新方法研究[J]. 船舶力学, 2003, 7(4):1-8. YING Liang-mei, SHEN Hong-cui. Study on a new method for the model test and speed performance prediction of single screw submarine[J]. Journal of Ship Mechanics, 2003, 7(4):1-8. |
| [2] |
杨仁友, 沈泓萃, 姚惠之. 带前置导叶桨潜艇自航试验的数值模拟与自航因子预报[J]. 船舶力学, 2005, 9(2):31-40. YANG Ren-you, SHEN Hong-cui, YAO Hui-zhi. Numerical simulation on self-propulsion test of the submarine with guide vanes and calculations for self-propulsion factors[J]. Journal of Ship Mechanics, 2005, 9(2):31-40. |
| [3] | BURCHER R, RYDILL L. Concepts in submarine design[M]. Cambridge:Cambridge University Press, 1995. |
| [4] |
潜艇船模水下阻力、自航试验规程:CB/Z 216-1987[S]. 北京:中国船舶工业总公司指导性技术文件, 1987. Model underwater resistance and self-propulsion test code for submarines:CB/Z 216-1987[S]. Beijing:Technological Guidance of CSSC, 1987. |
| [5] |
涂海文, 孙江龙. 基于CFD的潜艇阻力及流场数值计算[J]. 舰船科学技术, 2012, 34(3):19-25. TU Hai-wen, SUN Jiang-long. Numerical analysis of resistance and flow field of submarine based on CFD[J]. Ship Science and Technology, 2012, 34(3):19-25. |
| [6] | ZHANG Z R. Verification and validation for RANS simulation of KCS container ship without/with propeller[J]. Journal of Hydrodynamics, Series B, 2010, 22(5 S1):932-939. |
| [7] |
张文照, 肖昌润. 斜流中艇后螺旋桨水动力数值计算方法[J]. 舰船科学技术, 2014, 36(2):55-59. ZHANG Wen-zhao, XIAO Chang-run. Research on numerical calculation of behind-the-boat propeller hydrodynamic performance in oblique flow[J]. Ship Science and Technology, 2014, 36(2):55-59. |
| [8] |
黄璐, 陈立, 邱辽原, 等. 螺旋桨水动力性能及流固耦合数值模拟[J]. 舰船科学技术, 2014, 36(11):33-37. HUANG Lu, CHEN Li, QIU Liao-yuan, et al. Numerical simulation of hydrodynamic performance and fluid-structure interaction of propeller[J]. Ship Science and Technology, 2014, 36(11):33-37. |
 2016, Vol. 38
2016, Vol. 38
