目前,研究结构在爆炸载荷作用下的响应主要通过3种途径:试验方法、理论方法和数值仿真方法。试验方法最为直观,可信度最高,但囿于试验场地、试验设备要求严格,而且成本太高,所以很难广泛应用;由于爆炸问题的高度非线性,对于复杂结构,理论方法无法给出解析解;而数值仿真方法计算成本低,周期短,计算数据与实验实测数据基本吻合,因此该方法应用广泛[1, 2, 3]。
在研究船体结构的非接触爆炸(舱内或空中)响应的数值仿真分析中,其流固耦合面处理复杂,计算时间巨大。为了缩短计算时间,一般可根据爆炸冲击的特性、研究内容,选定舱段的分析范围。对于舱段结构的非接触爆炸响应,可建立三舱段模型,其中中间舱段为目标舱段,并在2个相邻舱段的末端施加边界约束[4]。边界条件尤其是舷外水的模拟会对舱段结构响应造成影响,过去在研究舱段结构的非接触爆炸响应时,有时会忽略舷外水的作用,直接在空气环境中进行数值仿真计算,导致对爆炸载荷作用后的结构毁伤极限强度的评估不够准确[1]。
为了分析舷外水对舱段结构抗爆响应的影响,本文运用有限元分析软件MSC.DYTRAN分别建立一般约束和将舷外水简化为附连水质量及水弹簧约束的三舱段结构有限元模型,并进行舱内爆炸和空中爆炸载荷作用下的数值仿真计算。对三舱段结构有限元模型2种不同的约束,就舱内爆炸和空中爆炸载荷作用下目标舱段响应测点的塑性变形作了对比分析。
1 基本控制方程理想气体爆炸冲击波的传播可用欧拉运动方程组描述,该方程组包含了三大守恒(质量守恒、动量守恒和能量守恒)的特性,采用矢量微分形式表示为[5, 6, 7]:
| $ \frac{{\partial { q}}}{{\partial t}}+\frac{{\partial { f}({ q})}}{{\partial x}}+\frac{{\partial { g}({ q})}}{{\partial y}}+\frac{{\partial { h}({ q})}}{{\partial z}}=0\text{,} $ | (1) |
式中q为状态矢量。fq,gq和hq分别定义如下:
| $ \begin{array}{l} { q}=\left\{ \begin{array}{l} {\rm{ }}\rho \\ \rho u\\ \rho v\\ \rho w\\ {\rm{ }}E \end{array} \right\};\quad\,{ f}({ q})=\left\{ \begin{array}{l} {\rm{ }}\rho u\\ {\rm{ }}\rho {u^2}+p\\ {\rm{ }}\rho uv\\ {\rm{ }}\rho uw\\ (E+p)u \end{array} \right\};\\ { g}({ q})=\left\{ \begin{array}{l} {\rm{ }}\rho v\\ {\rm{ }}\rho uv\\ \rho {v^2}+p\\ {\rm{ }}\rho vw\\ (E+p)v \end{array} \right\};\quad\,{ h}({ q})=\left\{ \begin{array}{l} {\rm{ }}\rho w\\ {\rm{ }}\rho uw\\ {\rm{ }}\rho vw\\ {\rm{ }}\rho {w^2}+p\\ (E+p)w \end{array} \right\}\text{。} \end{array} $ | (2) |
式中:ρ为材料密度;u,v,w为3个速度分量;E为总能量;p为流体压强。
将式(1)在空间域上用有限体积法的欧拉网格进行离散,然后在每个单元上求解欧拉方程。对每个单元表面求解过程中,每个单元表面都有一个左邻单元和右邻单元,因此把左邻单元和右邻单元的状态变量看作是单元表面法线方向的通量解的初始条件[6]:
| $ \tilde q(\tilde x\text{,}0)=\left\{ \begin{array}{l} {{\tilde q}^L}{\rm{ }}\tilde x \leqslant 0 \text{,}\\[7pt] {{\tilde q}^R}{\rm{ }}\tilde x \leqslant 0\text{。} \end{array} \right. $ | (3) |
式中$ \tilde q $为状态变量,基于以表面法线方向为x轴的局部坐标系。
2 有限元计算模型 2.1 三舱段有限元模型以某布置有3层甲板以及双层底的典型三舱段模型为研究对象。舱段总长40.5 m,型深12 m,型宽17 m,设计吃水5 m。通过2道横舱壁将舱段分为3个长度相同的舱室。舱段模型的典型横剖面见图 1。
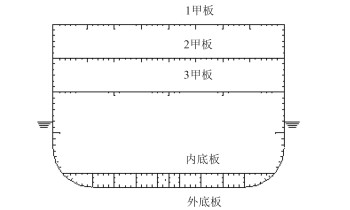
|
图 1 舱段模型典型横剖面 Fig. 1 Typical cross section |
在MSC.Patran中建立舱段三维有限元模型(见图 2)。为了提高计算效率,将纵骨、普通横梁等构件的小翼板等效至腹板高度内。

|
图 2 三舱段有限元模型 Fig. 2 Three-cabin FEM model |
舱段模型的材料为Q345钢,杨式模量E=210 Gpa,泊松比μ=0.3,密度ρ=7.8×103 kg/m3。通过基于Cowper-Symonds模型的本构方程来定义舱段模型材料的动应力[4],即
| $ \frac{{{\sigma _d}}}{{{\sigma _0}}}=1+{(\frac{{\dot \varepsilon }}{D})^{1/P}} \text{,} $ | (4) |
式中:σd为动应力;σ0为静应力;ε为等效应变率;D和P为材料常数,分别取40.5和5。
舱室内外空气采用理想气体状态方程描述,即Gamma方程:
| $ p=(\gamma -1)\cdot \rho \cdot {\rm{e}}\text{。} $ | (5) |
式中:γ=1.4,为比热比;ρ=1.25 kg/m3,为空气密度;e=2.1×105 J/kg,为空气比内能。
TNT炸药用高能高压空气来模拟,同样采用Gamma方程,初始条件下炸药密度ρd=1 600 kg/m3,比内能ed=4.2×106 J/kg。本文采用球形装药,舱内爆炸炸药半径取为0.310 m,装药量约为200 kg TNT;空中爆炸炸药半径取为0.195 m,装药量约为50 kg TNT。
2.3 舷外水的影响 2.3.1 附连水质量爆炸冲击波从产生到完全耗散的过程中,会诱导舱段发生振动。由于选取工况的装药在目标舱段1甲板的正上方或正下方(舱内),其舱段的爆炸冲击响应在水线以下部分以垂向为主。舷外水对舱段垂向冲击响应的惯性影响能够直接反映在参与舱段冲击响应过程中等效质量的改变上,一般把参与舱段运动的舷外水质量称为附连水质量,这部分附加质量跟舱段本身质量同一量级。可由下式计算附连水质量[8]:
| $ {m_{av}} = \frac{1}{2}{C_v}\rho {\rm{ }}\pi {b^2}。 $ | (6) |
式中:Cv为剖面修正系数,查F.M.刘易斯给出的图谱,得到2.1节舱段模型对应的剖面修正系数为1.15;b为设计水线半宽。
根据舱段的吃水和线型,计算得到舱段模型总的附连水质量为5 285.8 t,将这些质量平均分配到模型设计水线以下外板的单元节点上,每个节点分配到的质量为0.496 t。
2.3.2 水弹簧船体受到爆炸冲击波影响时,舷外水会对船体产生支撑作用,相当于船体梁的弹性基础,这种舷外水对船体的作用可简化为水弹簧来处理。由式(7)计算水弹簧的刚度[8]:
| $ K=\rho gS\text{。} $ | (7) |
式中S为船体水线面面积。
计算得到水弹簧的总刚度为6 747.3 N/mm,将这部分刚度平均分配到舱段外板与强框架相连接的节点上,每个节点分配到的刚度为3.05 N/mm。
2.4 边界条件与装药工况将舱段模型前后端面上的节点通过多点约束(MPC)与独立点相关联,独立点取为端面形心。在空气环境下模拟爆炸前端独立点约束为ux=uy=uz=rx=0,后端独立点约束为uy=uz=rx=0;考虑舷外水的影响模拟爆炸前端独立点约束为ux=uy=rx=0,后端独立点约束为uy=rx=0。
装药工况如图 3所示。装药位置沿船长方向及宽度方向位于舱段正中,沿高度方向选取Z=0.5 m,1.0 m,2.0 m,2.5 m(Z表示爆心与上甲板间的距离)。为了方便表示,将装药工况记为“工况P-Z”,P代表爆心位置(in表示舱内爆炸,out表示空中爆炸),并将空气环境下和考虑舷外水影响的结构模型分别记为Model 1和Model 2(例如Z=2 m,爆心位于舱外的装药工况记为工况out-2.0)。
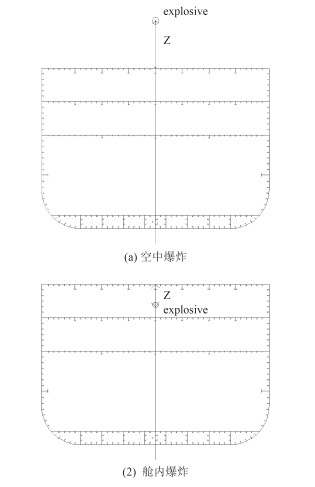
|
图 3 装药工况示意图 Fig. 3 Position of expoiosive |
在中间舱段的01甲板、1甲板、外底板上布置测点,测点布置情况见表 1。将各测点在各个时刻的位移响应值作为分析参考对象[9]。
| 表 1 舱段测点位置数据 Tab. 1 Position of measuring |
舱内爆炸计算总时长240 ms,共有2个工况:工况in-0.5、工况in-1.0。工况in-1.0下Model 1in-1.0和Model 2in-1.0在各个测点的位移时历曲线如图 4所示。
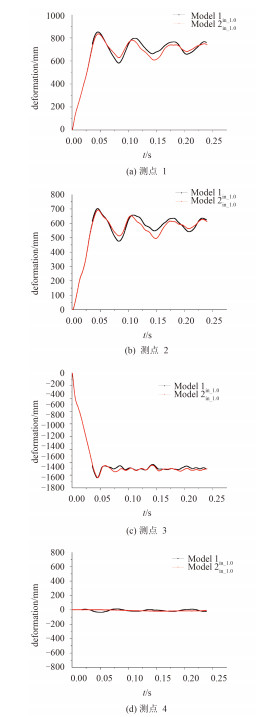
|
图 4 变形时历曲线 Fig. 4 Deformation curve |
测点1 ~测点3的变形时历曲线基本呈正弦指数衰减形式,而测点4的变形较小,可以忽略。下面的分析基于测点1 ~测点3的变形。至计算结束时,测点3的变形已基本稳定,但测点1和测点2的变形还未到稳定状态,因此需对测点数据进行拟合,拟合函数选为正弦指数衰减函数:
| $ y={y_0}+A{e^{-x/{t_0}}}\sin(\pi \frac{{x-xc}}{w})\text{。} $ | (8) |
工况in-1.0下Model in-1.0在测点1和测点2处的变形时历曲线拟合曲线如图 5所示,其他工况下2种模型在各个测点的变形时历曲线也做同样的处理。
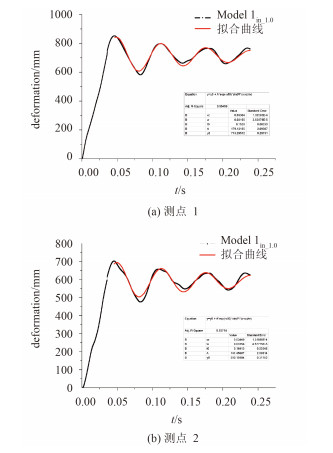
|
图 5 变形时历曲线拟合曲线 Fig. 5 Fitted deformation curve |
从上面的拟合曲线可以读出,变形稳定时,工况in-1.0下Model 1在测点1和测点2处的变形分别为713.3 mm和590.16 mm。
以测点1 ~测点3的最大变形值和稳定变形值为比较参数,比较2个模型在2个工况下的抗爆响应。测点的塑性变形值比较结果见表 2和表 3。
| 表 2 工况in-0.5下比较参数值 Tab. 2 Value of deformation in conditionin-0.5 |
| 表 3 工况in-1.0下各比较参数值 Tab. 3 Value of deformation in conditionin-1.0 |
从表 3可以看出,2个模型对应的的最大变形值差异不明显,如工况in-1.0下测点1对应Model 1和Model 2的最大变形值分别为851.25 mm和834.01 mm,最大相对差值为2.03%;2个模型对应的稳定变形值差异不明显,如工况in-1.0下测点1对应Model 1和Model 2的稳定变形值分别为731.30 mm和705.74 mm,最大相对差值为3.50%。可以认为在研究舱内爆炸问题时,舷外水的影响较小,可以忽略。
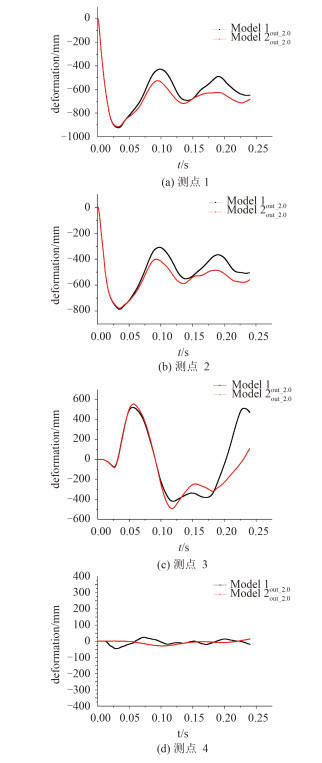
3.2 空中爆炸空中爆炸计算总时长240 ms,共有2个工况:工况out-2.0、工况out-2.5。工况out-2.0下Model 1 out-2.0和Model 2out-2.0在各个测点的位移时历曲线见图 6。
|
图 6 变形时历曲线 Fig. 6 Deformation curve |
测点1和测点2的变形时历曲线基本呈正弦指数衰减形式,测点3的变形则随时间分布较为杂乱,没有统一规律,测点4的变形较小,可以忽略。下面的分析基于测点1和测点2的变形。至计算结束时,各个测点的变形还未到稳定状态,因此需对测点数据进行拟合,拟合方法同3.1节。工况out-2.0下Model 1out-2.0在测点1和测点2处的变形时历曲线拟合曲线如图 7所示。

|
图 7 变形时历曲线拟合曲线 Fig. 7 Fitted deformation curve |
从上面的拟合曲线可以读出,变形稳定时,工况out-2.0下Model 1out-2.0在测点1和测点2处的变形分别为-595.87 mm和-464.49 mm。
以测点1和测点2的最大变形值和稳定变形值为比较参数,比较2个模型在2个工况下的抗爆响应。测点的塑性变形值比较结果见表 4和表 5。
| 表 4 工况out-2.0下各比较参数值 Tab. 4 Value of deformation in conditionout-2.0 |
| 表 5 工况out-2.5下各比较参数值 Tab. 5 Value of deformation in conditionout-2.5 |
从上表可以看出,在结构变形过程中,2个模型对应的最大变形值差异不明显,最大相对差值为1.28%;2个模型对应的稳定变形值差异则比较明显,最小相对差值为9.52%,最大相对差值为14.2%。可以认为在研究空中爆炸问题时,舷外水的影响必须计及。
4 结语通过计算和结果分析,得到以下结论:1)在研究舱内爆炸问题时,舷外水对舱段结构抗爆响应的影响很小,在具体计算时,可以不考虑舷外水的作用,直接在空气环境中模拟舱段爆炸;2)在研究空中爆炸问题时,舷外水对舱段结构抗爆响应的影响不能忽略。3)由于舱段塑性变形会影响船体毁伤极限强度准确评估,为此准确简化边界约束十分重要。
| [1] |
马春燕. 水面舰艇新型抗损结构设计与剩余强度研究[D]. 哈尔滨:哈尔滨工程大学, 2006. MA Chun-yan. Study for new structure design of warship resisting damage and residual strength[D]. Harbin:Harbin Engineering University, 2006. |
| [2] |
张延昌, 王自力, 顾金兰, 等. 夹层板在舰船舷侧防护结构中的应用[J]. 中国造船, 2009, 50(4):36-44. ZHANG Yan-chang, WANG Zi-li, GU Jin-lan, et al. Application of sandwich panel in anti-shock design of warship's side structure[J]. Shipbuilding of China, 2009, 50(4):36-44. |
| [3] |
马欣, 张延昌, 王自力. 水下非接触爆炸载荷下双层底结构单元抗冲击性能研究[J]. 舰船科学技术, 2008, 30(6):39-43. MA Xin, ZHANG Yan-chang, WANG Zi-li. Research on the anti-shock capacity of double bottom cell due to UNDEX[J]. Ship Science and Technology, 2008, 30(6):39-43. |
| [4] |
吴迪, 张世联. 空中爆炸下舰船动态响应数值模拟[J]. 舰船科学技术, 2007, 29(6):165-168. WU Di, ZHANG Shi-lian. Numerical simulation of the dynamic response of ship under air explosion[J]. Ship Science and Technology, 2007, 29(6):165-168. |
| [5] |
李翼祺, 马素贞. 爆炸力学[M]. 北京:科学出版社, 1992. LI Yi-qi, MA Su-zhen. Mechanics of explosion[M]. Beijing:Science Press, 1992. |
| [6] | MSC. Dytran User's Manual[DB/CD]. Los Angeles:MSC Corporation, 2005. |
| [7] |
万力, 吴莘馨, 卞文杰. 瞬态动力学CAE解决方案MSC. Dytran实例教程[M]. 北京:北京大学出版社, 2004. WAN Li, WU Xin-xin, BIAN Wen-jie. The instance tutorial of transient dynamics CAE solutions MSC. Dytran[M]. Beijing:Peking University Press, 2004. |
| [8] |
金咸定, 赵德有. 船体振动学[M]. 上海:上海交通大学出版社, 2000. JIN Xian-ding, ZHAO De-you. Ship vibration[M]. Shanghai:Shanghai Jiaotong University Press, 2000. |
| [9] |
王佳颖, 张世联, 徐敏. 接触爆炸下舰船强力甲板塑性动态响应特性研究[J]. 中国舰船研究, 2010, 5(5):10-14, 21. WANG Jia-yin, ZHANG Shi-lian, XU Min. Plastic dynamic response characteristics of warship's strength deck under contact explosion[J]. Chinese Journal of Ship Research, 2010, 5(5):10-14, 21. |
 2016, Vol. 38
2016, Vol. 38
