2. 骆驼集团股份有限公司, 湖北 襄樊 441100
2. Camel Group Corporation Ltd., Xiangfan 441100 China
复合材料结构集承载与吸声功能于一体,并且具有振动阻尼性能好、浮性高、磁信号低、容易成型等优点,目前应用于许多领域,例如飞机机舱、潜艇和汽车制造等。将新型复合材料用于潜艇壳体的制造,可以实现潜艇隐身技术和综合性能的跨越式发展。虽然潜艇隐身技术已经取得很大进步,但国外从未停止过对新型潜艇声隐身技术的探索与研究,近期提出并开展了一些非传统的隐身技术及概念研究[1]。潜艇声隐身研究可转化为复合材料圆柱壳声隐身研究,通过降低声目标强度,使潜艇不易被敌方声呐探测。
过去几十年,许多研究人员致力于研究复合材料结构的声学特性。石勇[2]运用传递矩阵法研究了三明治夹芯板材结构的声学性能,结果表明,表层越薄,夹层结构的声反射越小,吸声系数越大;王华玉[3]对表面敷设粘弹性吸声材料的物体目标强度进行研究,并以单壳体和双壳体圆柱壳模型为例,对表面敷设均匀吸声层和含腔吸声层不同情况下进行仿真计算;张玉玲[4]研究了敷设吸声材料复杂目标的目标强度计算方法,并利用板块元法计算复杂目标敷设吸声层前后的目标强度,结果表明,低频1~30 kHz时,吸声效果不明显,随着频率增大,敷设吸声材料后的目标强度降低值越大;邱力莹[5]运用面向对象有限元法研究了水声吸声覆盖层的声学特性,通过改变吸声材料的物理参数,分析了吸声材料厚度、密度、杨氏模量、泊松比和损耗因子对声反射特性的影响,并计算了无空腔均匀层吸声覆盖层的声反射系数;Seyyed[6, 7]运用传递矩阵法研究了水下FGM圆柱壳声散射问题,并分析了材料参数对FGM圆柱壳形态函数的影响。大量研究人员着重研究复合材料板材结构或敷设消声瓦的圆柱壳及FGM圆柱壳的声学性能,但是复合材料圆柱壳的声散射问题的研究较少,本文着重于铺层角度、纤维层数及壳厚比对复合材料圆柱壳的声目标强度影响规律研究,并进行理论分析与对比,为复合材料圆柱壳的设计提供一定的依据。
1 数值分析数值方法在20世纪80年代得到了广泛应用,边界元法[8]是对边界采用有限的概念,减少空间维数,使计算机内存的占用和运算时间均减少,但只能给出边界上的量值,无法深入到物体内部,只要结构发生更改,就必须对边界作修改。在水声领域应用最广泛的是有限元法,对单元结构、流体和界面进行网格离散,考虑流体介质对吸声结构的影响,在流固边界设置耦合单元,并采用AML自动匹配声辐射边界条件技术研究研究吸声结构的平面声波散射问题。
AML技术是在PML技术上发展的是新型仿真方法,根据给定的声学有限元辐射边界,自动地根据物理模型定义吸收层和吸声边界条件。不仅提高了计算精度,而且降低了工作计算量,提高了计算速度。AML方法能够根据给定的计算频率自动生成并调整PML层,提高了低频和高频计算精度。
1.1 数值分析原理声学数值计算方法可以分为声学有限元法、声学边界元法、声线法和统计能量法等。有限元法可应用于以任何微分方程描述的各类物理场中,其在声学方程求解上发展了很多年,根据波动方程,使用有限元法将其离散后,并根据相应的边界条件即可求出声场。针对固-固边界,应用法向、切向应力分别连续、各方向的质点位移连续;针对固-流边界,应用固体中的法相应力与水中声压大小相等、符号相反,固体与流体中法向质点位移连续、切向应力和位移均为0;针对固-空界面,其界面近似为自由界面,则法向和切向应力均为0。
声学波动方程[8]为:
| $ {\nabla ^2}p(x,y,z)-{k^2}p(x,y,z)=-j{\rho _0}\omega {q_0}(x,y,z)\text{,} $ | (1) |
对式(1)进行积分得:
| $ \begin{array}{l} \displaystyle\int\limits_V {\widetilde P} \left({{\nabla ^2}p(x,y,z)-{k^2}p(x,y,z)+} \right.\\ \quad\quad\quad\quad\quad\quad\quad\quad \left.{j{\rho _0}\omega {q_0}(x,y,z)} \right){\rm d}V=0\text{。} \end{array} $ | (2) |
式中:$\widetilde P $为权函数;V为计算域。
根据高斯理论,由式(2)知
| $ \begin{array}{*{20}{l}} {\int\limits_V {(\nabla \tilde P} \cdot \nabla P){\rm{d}}V - {\omega ^2}\int\limits_V {(\frac{1}{{{c^2}}}\tilde P} \cdot P){\rm{d}}V = }\\ {\int\limits_V {j\tilde p} {\rho _0}\omega {q_0}{\rm{d}}V - \int\limits_s {j\tilde p{\rho _0}\omega v \cdot n{\rm{d}}s} \quad \quad {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \quad } \end{array} $ | (3) |
将式(3)进行有限元网格离散,并整理得到数值形式的方程组
| $ {W_a} \cdot {P_i} = {F_i}。 $ | (4) |
式中:Wa稀疏矩阵;Fi为边界条件。
在给定边界条件下,对稀疏矩阵求逆即可算出声场。运用AML技术,根据给定的平面波,自动地根据圆柱结构定义吸收层和吸声边界条件,即可求得散射声场。
1.2 仿真计算模型本文研究的模型是复合材料圆柱壳体,数值仿真铺层角度、纤维层数及壳厚比对复合材料圆柱壳体的影响规律。复合材料圆柱壳长为0.6 m,半径为0.08 m,采用Shell进行建模,网格类型为S4R;水域采用体单元进行建模,网格类型为C3D8R,单元总数为5 818。圆柱壳两端为钢结构,圆柱壳壳体结构材料为各向异性材料,材料参数如表 1所示。铺层角度为纤维层主方向1与圆柱壳轴方向的角度,圆柱壳轴方向转向纤维层主方向1逆时针为正。
| 表 1 圆柱壳壳体材料参数 Tab. 1 Cylindrical shell material parameters |
许多研究人员调查研究了铺层角度对纤维增强结构失效机理的影响。对于纤维增强圆柱耐压薄壳结构[9, 10],环向应力与轴向应力2:1时,争对结构的失效模式,铺层角度55°为最优解;Rosenow[10]运用层合板理论分析铺层角度为15° ~ 85°对管道结构应力、应变的影响,并与实验进行对比,结果表明,针对结构失稳模态,环向应力与轴向应力2:1时,铺层角度55°最好,没有轴向应力时,铺层角度75°为最优解。同样,铺层角度对纤维缠绕结构的声学特性也有一定的影响。研究铺层角度,既可满足结构不失稳条件,又满足结构的声学特性。
复合材料圆柱壳壳体结构材料为正交各向异性材料,产生的散射波分为刚性散射波和弹性散射波,刚性散射波与几何形状有关,弹性散射与材料参数(弹性模量、密度、泊松比和损耗因子等)有关。随着铺层角度不同,产生的纵波和横波波速发生变化,导致产生的散射声场不一样,声目标强度值不同。复合材料圆柱壳厚度为5 mm,仿真计算的频率范围为1 ~ 15 kHz,保证壳厚度不变,改变铺层角度,铺层角度分别为0°,(±30°)8,(±55°)8,(±80°)8,分别研究圆柱壳在正入射和斜入射(入射角为30°,60°)下的声学特性。
2.1.1 正入射时铺层角度对声目标强度的影响图 1为正入射下铺层角度对复合材料圆柱壳的TS的影响规律,由图 3知,正入射下,低频时(1 ~ 2.5 k),铺层角度为0°时TS值较低;中频时(2.5 ~ 8 k),除了个别频率点,铺层角度为(±30°)8时TS值较低;高频时8 ~ 15 k,随着频率增大,铺层角度对TS的影响不大,且铺层角度为(±30°)8,(±55°)8时TS值最大值较小。对于均质圆柱壳,低频时的TS值明显低于中高频下的TS值,由图 1知,铺层角度为0°时TS变化规律与均质圆柱壳类似,铺层角度为±30°,±55°,±80°时,低频下的TS值明显高于中高频下的情况。

|
图 1 正入射下铺层角度对复合材料圆柱壳 TS 的影响 Fig. 1 Influence of ply angle on the TS of cylindrical shell under normal incidence |
图 2为入射角为30°时铺层角度对复合材料圆柱壳TS的影响规律,图 3为入射角为60°时铺层角度对复合材料圆柱壳TS的影响规律。由图 2知,入射角为30°时,低频角度为(±30°)8时TS值最大值最小,约为-25 dB;频率为6 ~ 15 k时,角度为(±55°)8时TS值最小。由图 3知,入射角为30°时,低频时(1 ~ 2 k),铺层角度为0°时TS值较低;频率为2 ~ 7 k时,铺层角度为(±30°)8时TS值最大值最小,约为-33 dB;频率为8 ~ 15 k时,铺层角度为±30°,±55°,±80°时,其TS随频率的变化基本吻合。
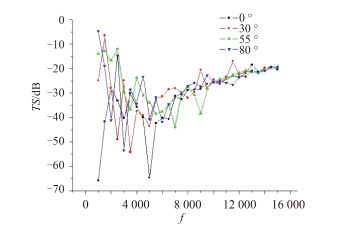
|
图 2 入射角为 30° 时铺层角度对复合材料圆柱壳 TS 的影响 Fig. 2 Influence of the ply angle on the TS of cylindrical shell with oblique incidence 30° |
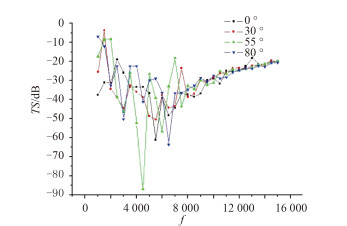
|
图 3 入射角为 ± 60° 时铺层角度对复合材料圆柱壳 TS 的影响 Fig. 3 Influence of the ply angle on the TS of cylindrical shell with oblique incidence ± 60° |
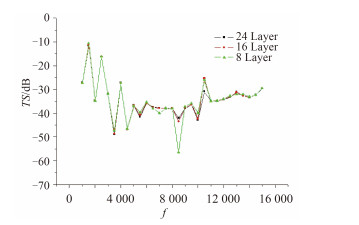
因复合材料各向异性,不同于均质材料,纤维的厚度对圆柱壳声目标强度有一定的影响。通过工艺上的要求,可以改变每层纤维的厚度。保证圆柱壳的厚度不变,改变纤维层数,计算频率为1 ~ 15 kHz,仿真分析正入射下纤维层数对水下空气背衬条件下复合材料圆柱壳TS的影响规律。由图 4知,正入射下,铺层角度为±30°时,低频(1 ~ 4 k)时,纤维层数对圆柱壳声目标强度的影响随频率变化一致;频率增大时,纤维层数为16层时圆柱壳声目标强度最小。由图 5知,正入射下,铺层角度为±55°时,低频(1 ~ 2.5 k)时,纤维层数对圆柱壳声目标强度的影响随频率变化一致;频率4.5 ~ 15 k时,纤维层数为16层时圆柱壳声目标强度最小。由图 6知,铺层角度为±80°时,频率为1 ~ 6 k时,铺层角度对圆柱壳声目标强度的影响一致;频率为6 ~ 15 k时纤维层数为24层时圆柱壳声目标强度最小。
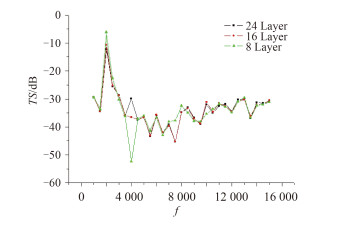
|
图 4 铺层角度 ± 30° 时纤维层数对 TS 的影响规律 Fig. 4 Influence of fiber layer on the TS with ply angle ± 30° |
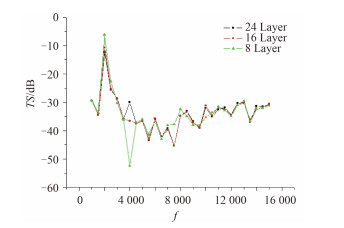
|
图 5 铺层角度 ± 55° 纤维厚度对 TS 的影响规律 Fig. 5 Influence of fiber layer on the TS with ply angle ± 55° |
|
图 6 铺层角度±80°纤维厚度对TS的影响规律 Fig. 6 Influence of shell thickness ratio on the TS with ply angle ± 80° |
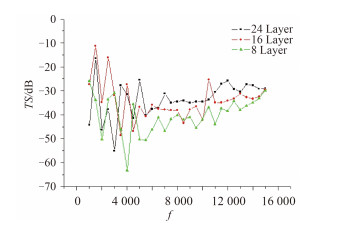
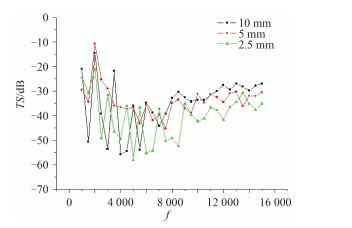
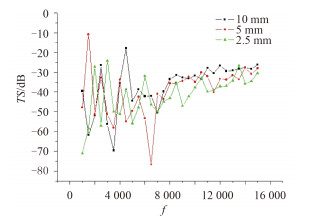
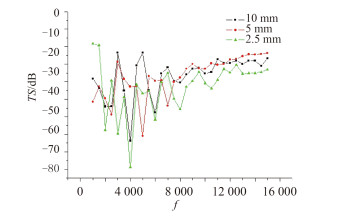
图 7 ~图 10分别是铺层角度为±80°,±55°,±30°,0°时,计算频率为1 ~ 15 kHz,不同壳厚比声目标强度随频率变化的规律。由图 7知,铺层角度为±80°时,频率处于1 ~ 5 k区间时,壳厚度为2.5 mm时声目标强度值最大值最小,最大值约为-25 dB左右;频率为5 ~ 15 k时,壳厚度为2.5 mm时声目标强度值小于壳厚5 mm和壳厚10 mm的声目标强度值。由图 8知,铺层角度为±55°时,频率处于1 ~ 6 k区间时,壳厚度为2.5 mm时声目标强度值最大值最小,最大值约为-20 dB左右;频率为6 ~ 15 k时,除了个别频率点,壳厚度为2.5 mm时声目标强度值小于壳厚5 mm和壳厚10 mm的声目标强度值。由图 9知,铺层角度为±30°时,频率处于1 ~ 7 k区间时,壳厚度为2.5 mm时声目标强度值最大值最小,最大值约为-25 dB左右;频率为7 ~ 15 k时,除了个别频率点,壳厚度为2.5 mm时声目标强度值小于壳厚5 mm和壳厚10 mm的声目标强度值。由图 10知,铺层角度为0°时,频率处于2 ~ 7.5 k区间时,壳厚度为2.5 mm时声目标强度值最大值最小,最大值约为-35 dB左右;频率为7.5 ~ 15 k时,壳厚度为2.5 mm时声目标强度值明显小于壳厚5 mm和壳厚10 mm的声目标强度值。因而得出结论,在一定频率范围内,壳厚比越小,声目标强度值越小。圆柱壳厚度越小时,透声性能越好,吸声系数越大,散射声压值越小,相应的声目标强度值也越小。
|
图 7 铺层角度 ± 80° 壳厚比对 TS 的影响规律 Fig. 7 Influence of shell thickness ratio on the TS with ply angle ± 80° |
|
图 8 铺层角度 ± 55° 壳厚比对 TS 的影响规律 Fig. 8 Influence of shell thickness ratio on the TS with ply angle ± 55° |
|
图 9 铺层角度 ± 30° 壳厚比对 TS 的影响规律 Fig. 9 Influence of shell thickness ratio on the TS with ply angle ± 30° |
|
图 10 铺层角度 0° 壳厚比对 TS 的影响规律 Fig. 10 Influence of shell thickness ratio on the TS with ply angle 0° |
复合材料圆柱壳因其非均匀性,不同于均质圆柱壳,除了材料参数(密度、杨氏模量、泊松比、损耗因子等)对声目标强度有影响,本文基于数值仿真方法研究其他参数(铺层角度、铺层层数和壳厚比)对圆柱壳TS的影响。综合上述仿真计算,得到以下结论:
1)低频时,正斜入射下,铺层角度为0°时,复合材料圆柱壳的声目标强度值最小;中频时,正斜入射下,铺层角度为±30°时,复合材料圆柱壳的声目标强度值最大值最小。
2)低频和高频时,正入射下,圆柱壳厚度不变时,铺层层数对圆柱壳声目标强度值影响不大;中频时,铺层角度相同时,铺层层数对圆柱壳声目标强度值有一定的影响。
3)高频时,正入射下,壳厚比较小的复合材料圆柱壳TS明显小于其他情况。这是因为圆柱壳厚度越小时,透声性能越好,吸声系数越大,散射声压值越小,相应的声目标强度值也越小。
| [1] |
苏强, 王桂波, 朱鹏飞, 等. 国外潜艇声隐身前沿技术发展综述[J]. 舰船科学技术, 2014, 36(1):1-9. SU Qiang, WANG Gui-bo, ZHU Peng-fei, et al.Summarize of foreign submarine acoustic stealth frontier technologies development[J]. Ship Science and Technology, 2014, 36(1):1-9. |
| [2] |
石勇. 夹层复合材料水下声隐身舵的研究[D]. 武汉:海军工程大学, 2006. SHI Yong.Study on the sandwich composites rudder for acoustical stealth underwater[D]. Wuhan:Naval University of Engineering, 2006. |
| [3] |
王华玉. 复合圆柱壳目标特性研究[D]. 哈尔滨:哈尔滨工程大学, 2012. WANG Hua-yu.The research on target characteristics of composite cylindrical shell[D]. Harbin:Harbin Engineering University, 2012 |
| [4] |
张玉玲, 陶猛, 范军. 敷设吸声材料复杂目标的目标强度计算[J]. 上海交通大学学报, 2009, 43(8):1322-1326, 1331. ZHANG Yu-ling, TAO Meng, FAN Jun. Target strength calculation of underwater complicated targets coated with absorbing materials[J]. Journal of Shanghai Jiaotong University,2009, 43(8):1322-1326, 1331. |
| [5] |
邱力莹. 用面向对象有限元方法研究水声吸声覆盖层声反射特性[D]. 哈尔滨:哈尔滨工程大学, 2009. QIU Li-ying.The research on the acoustic characteristics of underwater anechoic coating by OOFEM[D]. Harbin:Harbin Engineering University, 2009. |
| [6] | HASHEMINEJAD S M, RAJABIM. Acoustic resonance scattering from a submerged functionally graded cylindrical shell[J]. Journal of Sound and Vibration, 2007, 302(1/2):208-228. |
| [7] | HASHEMINEJAD S M, ABBASION S, MIRZAEIY. Acoustic pulse interaction with a submerged functionally graded material hollow cylinder[J]. Acoustical Physics, 2011, 57(1):20-35. |
| [8] |
詹福良, 徐俊伟. Virtual. Lab. Acoustics声学仿真计算从入门到精通[M]. 西安:西北工业大学出版社, 2013. ZHAN Fu-liang, XU Jun-wei. Virtual. Lab. Acoustic simulation calculation from entry to the essence[M]. Xi'an:Northwestern Polytechnical University Press, 2013. |
| [9] | MISTRYJ, GIBSON AG, WU YS. Failure of composite cylinders under combined external pressure and axial loading[J]. Composite Structures, 1992, 22(4):193-200. |
| [10] | ROSENOW MWK. Wind angle effects in glass fiber-reinforced polyester filament woundpipes[J]. Composites, 1978, (9):17-24. |
 2016, Vol. 38
2016, Vol. 38
