水下航行体在航行时，水舱与外部流场通过流水孔产生流体交换，这一过程会产生额外的阻力及噪声；尤其是高速航行时，流水孔噪声快速增加，影响艇体的快速性及隐蔽性。国内外学者针对不同模型进行了数值仿真及试验研究：张楠^[1]对某翼型开孔艇体模型做了较为详细的数值计算，提出了流水孔流场模拟的数值方法；Rossiter在做了系列噪声试验的基础上，提出了空腔噪声的半经验公式；衣云峰^[2]对水下孔腔噪声做了相关试验，在Rossiter公式上做了修正。总体看来，影响开孔艇体流场及声场特性的因素较多^[3]。本文针对水舱开孔的长宽比这一因素，通过对已有试验模型做对应仿真分析，采用DES计算流场信息，求解FW-H获取声场信息，研究水舱开孔长宽比的噪声特性。

采用RANS结合DES方法获得流场数据，其中RANS模型控制方程为：

式中：P_k和P_ω为湍流生成项；f₁为混合函数；$ {\sigma _k}=2$，${\alpha _2}=0.44$，$ {\beta _2}=0.082 \,8$，$ {\sigma _{\omega 2}}=0.085 \,6 $均为经验系数；μ_t为涡黏系数。其中k方程耗散项中，湍流尺度参数$ {l_{k-\omega }}={k^{1/2}}/({\beta _k}\omega)$，而在DES模型中，当湍流尺度$ {l_{k-\omega }} > {C_{DES}}\Delta $（常数$ {C_{DES}}\Delta=0.65 $，Δ为网格尺度）时转换成大涡模拟模型，当湍流尺度${l_{k-\omega }} \le {C_{DES}} $时，该模型转换成SST k-ω湍流模型。而将所求得的流场数据在FW-H模型中求取其声场信息。其方程为：

式中：f为隐函数，描述运动物体边界控制面方程；V_i为物体表面的运动速度沿x_i轴方向的分量；P_ij为应力张量，为

研究对象为带有内部水舱的艇体模型，总长4.5 m，其中平行中体长1.6 m，回转体部分半径为0.3 m，带上层建筑后最大高度为0.33 m（距回转轴）。

在艇体首部安装水舱，水舱首端距艇首0.5 m，尾端距艇首0.9 m，保持开孔面积为0.025 6 m²，设置长宽比α为0.25，0.5，1，2，4；编号为A，B，C，D，E。

图 1(Fig. 1)

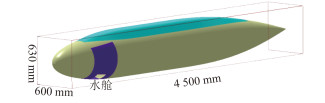
图 1 光体模型 Fig. 1 The hull model

本文前期进行了模型定流场的系列计算，确定选取SST k-ω两方程RANS湍流模型，并设置网格如图 2所示，模型取半网格量为234万。

图 2(Fig. 2)

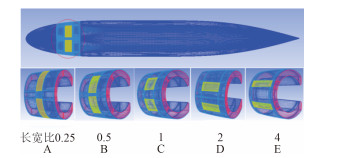
图 2 不同长宽比模型网格示意图 Fig. 2 The series models of different L/B ratio

在声场计算之前，为确保定流场计算的准确性，设计了5组来流工况，并将计算结果与试验结果进行对比，结果见表 1。按照统一建模方法划分网格，设置边界条件如下：

表 1(Tab. 1)

表 1 各开孔模型阻力系数计算结果Tab. 1 Calculating results of each model 序号 速度V/m·s–1 8.0 8.2 8.4 8.6 8.8 A 计算值（×103） 2.75 2.88 3.01 3.15 3.29 试验值（×103） 2.77 2.78 2.65 2.76 2.65 误差/% –0.9 –1.0 –1.4 –1.1 –1.7 B 计算值（×103） 2.76 2.86 3.00 3.14 3.33 试验值（×103） 2.78 2.91 3.03 3.18 3.42 误差/% –0.8 –1.7 –1.0 –1.4 –2.6 C 计算值（×103） 2.72 2.85 2.97 3.12 3.28 试验值（×103） 2.65 2.82 2.96 3.10 3.25 误差/% 2.8 1.0 0.5 0.5 0.7 D 计算值（×103） 2.79 2.93 3.06 3.21 3.34 试验值（×103） 2.76 2.90 3.08 3.23 3.40 误差/% 1.3 1.0 –0.5 –0.9 –1.6 E 计算值（×103） 2.71 2.81 2.95 3.11 3.32 试验值（×103） 2.65 2.79 2.99 3.16 3.28 误差/% 2.2 0.8 –1.2 –1.5 1.3

表 1 各开孔模型阻力系数计算结果 Tab. 1 Calculating results of each model

1）速度入口边界：距艇首约一倍艇长，来流速度为V_in=V=8.4 m/s；

2）压力出口边界：距艇尾约5倍艇长，设定好相对参考点的流体静压值；

3）流域外部边界：距艇体表面约一倍艇长，速度与主流域一致；

4）艇体表面边界：包括艇体外表面，水舱内侧壁面以及孔壁面等，设定为无滑移条件。

设置好边界条件后，选择SST k-ω两方程模型，使用SIMPLE算法求解方程，对流项和扩散项采用QUICK差分格式。待定流场计算稳定后，设置湍流模型为DES模型，进行瞬时流场计算，设置时间步长为0.000 5 s；待表面压力出现周期性变化后，开始采集相关流场信息，共计算20 000步。

对于水舱开孔问题研究，首先要求得一个准确的定流场，在前期的试验中，获得了较为可信的试验结果。可为本文的数值计算结果提供可靠的对比。

本文计算结果与修正后的试验数值较吻合，在此定流场基础上可计算得到瞬时流场信息。

低速湍流流经腔体时会引起腔体内部流场的自激振荡并向外辐射噪声，而对于开孔水舱，其结构比典型空腔更为复杂（见图 3），流体经由开孔进入水舱时，会在开孔附近及水舱内产生涡旋，导致孔壁面及水舱壁面的压力脉动，这是典型的偶极子噪声；而孔附近及水舱内的涡脱落则产生四极子噪声。

图 3(Fig. 3)

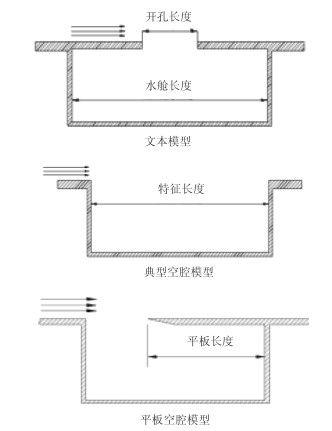
图 3 不同腔体平面对比示意图 Fig. 3 Different cavity types

刘敏^[4]计算得到了带开孔回转体的声场指向性，指出沿着开孔径向声压级最大。据此，本文沿开孔径向设置1#水听器（水舱中心）、2#水听器（距离回转轴0.5 m），如图 4所示。计算结束后，处理采集到的各水听器声信号。

图 4(Fig. 4)

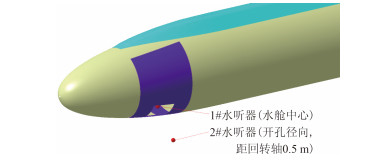
图 4 1#、2# 水听器位置示意图 Fig. 4 Position of 1#, 2# receiver

在气动声学中的空腔问题中，高速流经过空腔时，在腔内形成各种涡；随着孔腔长深比或形状的改变，产生尾涡或者剪切层模式，在腔底部及边缘处有着不同的涡脱落现象。与之不同，本文中的水舱内涡旋流速较低，该部分产生的涡脱落不似如此明显。为探究舱内流情况，可分析其流动过程，绘制B开孔水舱局部流线图（见图 5）。

图 5(Fig. 5)

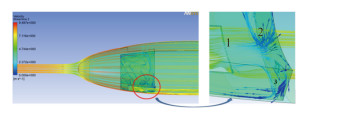
图 5 B 开孔模型局部流线图 Fig. 5 Localstreamline of model B

观察到流体流经开孔水舱的过程为：

1）流体到达开孔拐角时，发生分离，部分撞击舱壁，部分直接进入水舱内；

2）与水舱内流体掺混，速度下降，并撞击后部舱壁；

3）流体在水舱内形成涡旋，部分流体经由开孔流出，与外部流掺混。

流体在水舱内的流动会产生噪声，一般情况下，其流噪声水平影响因素包括来流速度、开孔面积、开孔个数等。而从本文计算结果中发现不同长宽比对流噪声水平也有影响。提取上节系列开孔模型水听器的总声压级，绘制对比图（见图 6）。

图 6(Fig. 6)

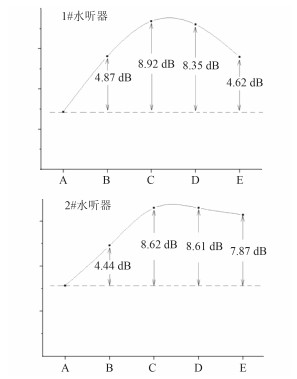
图 6 1#和2# 水听器总声压级对比图 Fig. 6 Thesound pressure level of 1#, 2# receiver

在长宽比α=0.25时，艇体产生的流噪声水平最低，表现为对α的增长较为敏感；而当α≥1时，随着α的进一步增长，总声压级并未出现明显增长。

资料表明，空腔的形状对腔内流动的影响很大，而不同的流动模式导致不同程度的声辐射^[5]；同样地，本文水舱因为长宽比的改变，导致孔腔入口局部的形状变化，使得声辐射程度也不尽相同。结合水舱内流动特点，在开孔长度（沿来流方向）较短时，内外流掺混程度低，在孔壁及舱壁上产生的压力脉动幅值相对较小；当开孔长度进一步增加，掺混更为强烈，总噪声水平升高；而当掺混达到一定程度，来流在开孔与水舱内所形成的脉动压力及涡脱落维持在一个较高的水平，此时总噪声水平不随开孔长度增加而继续增加。单孔平板模型可作为单孔吸声结构，不同开孔模型所形成结构的吸声频率也不尽相同^[6]，也会对总的流噪声水平产生一定影响。

1#水听器在水舱内，主要监听内部涡旋强度，可发现在长宽比为0.25时，内部涡旋强度要弱很多，说明此时涡旋强度对开孔长度更为敏感。

从上述分析可知，水舱表面开孔后，艇体表面的连续性和光滑性得到了破坏；外部流体经由流水孔进入水舱内部，与舱内流体进行交换，期间会产生偶极子和四极子噪声。分析声源的成分有助于进一步了解水舱开孔噪声的特性。同样地，可借鉴较为成熟的空腔研究。空腔流动中噪声的特征频率和来流速度以及空腔尺寸有关，大都采用Rossiter半经验公式：

式中：St为空腔振荡的斯特劳哈尔数；f_n为空腔振荡的频率；L为特征长度；U₀为来流速度；Ma为来流马赫数；n为模态阶数；并有由试验确定的常数α=0.25，k_v=0.57。学者们不断对其进行修正，衣云峰^[5]从水洞中试验结果出发，提出了水下圆柱孔腔噪声计算公式：

在讨论空腔问题的长深比影响时，特征长度均为空腔长度，而D.Rose^[7]提到：在空腔流动问题中当腔内有其他物体存在时，不能简单以此作为特征长度。司海清^[8]在研究高马赫数、高雷诺数的超高速流通过带平板空腔问题时（见图 4）发现由于平板的存在，可将空腔分成2个部分：一部分为空腔前缘与平板前缘之间的空腔；另一部分位于平板和空腔后缘角之间，视为闭式空腔，并且后者在整个的空腔流中占主导地位，并据此将平板长度作为特征长度。本文按照这个结论进行试算，发现并不适用于水下低速流动问题。

将2#水听器的声场数据在频域内进行FFT转换，并绘制其频谱图（见图 7）。

图 7(Fig. 7)

图7 系列开孔频谱图 Fig. 7 Spectrum map of series model

开孔水舱，涉及到水舱长度和开孔长度，需对此进行辨别。对本文及相关计算（文献[4]中水舱模型）的结果进行分析如表 2所示。

表 2(Tab. 2)

表 2 St数计算表Tab. 2 Calculating table of St number 模型 U0/m·s–1 fn l1 St1 l2 St2 注：l1 为腔体长度；l2 为开孔长度。 文献中模型 4.5 88.9 1 m 19.76 0.035 0.69 本文模型C 8.4 27.7 0.4 m 1.32 0.16 0.53

表 2 St数计算表 Tab. 2 Calculating table of St number

根据斯特劳哈尔公式计算得到的结果可知，将开孔长度作为特征长度更合适。以此来外推式（5），得到本文模型的各界模态特征频率，并与从数值计算结果中提取的特征频率作比较，如表 3所示。

表3(Tab. 3)

表 3 各开孔模型流噪声特征频率Tab. 3 Theeigenfrequency of each model L/B 0.25 0.5 1 2 4 L/m 0.08 0.113 0.16 0.226 0.32 1 阶 计算 48.3 39.6 27.7 20.6 14.8 理论 58.4 41.4 29.2 20.7 14.6 差别/% –17 –4 –5 0 1 2 阶 计算 96.3 72.6 50.5 38.4 28.2 理论 117.3 83.1 58.7 41.5 29.3 差别/% –18 13 14 –8 –4 3 阶 计算 144.6 114 77.6 58.7 44.3 理论 185 131 92.5 65.5 46.3 差别/% –22 –13 –16 –10 –4

表 3 各开孔模型流噪声特征频率 Tab. 3 Theeigenfrequency of each model

结果显示特征频率随开孔长宽比的变化而改变，并与计算结果吻合较好，由此可验证计算本文模型声场的特征长度是开孔在来流方向的距离，即图 3中的开孔长度。同时可发现：

1）总体上，随着长宽比的增加（即在来流方向上开孔长度越大），特征频率逐渐降低，符合一般声学规律；

2）经验公式在预测本文模型一阶模态特征频率时较准确，但在高阶时不够准确；

3）经验公式在预测开孔长度较大模型时较为准确，而在长宽比较小时不够准确。

在总噪声中贡献最大的部分决定了整体噪声的特征频率。结合上文对特征频率的分析，可判断出由于内外流的交换在孔壁上产生的压力脉动以及孔壁附近的涡脱落噪声为声源主要成分。

为验证上述针对特征频率的推论，可建立对应简化模型如图 8所示，设置开孔长度分别为20 mm，40 mm，80 mm，其余几何信息如图中所示，编号为A₁ ~ A₃。在孔中心、腔中心处设置水听器；在XY平面内以开孔为中心，半径为1 m的圆及YZ平面内以开孔为中心，半径为0.5 m的圆上等间距分布适量水听器。

图8(Fig. 8)

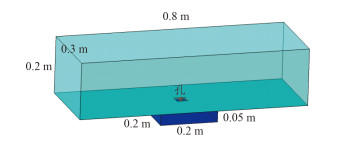
图 8 系列开孔频谱图 Fig. 8 Spectrum map of series model

绘制各简化模型的频谱图如图 9所示，将对应的特征频率进行总结，按照上述结论，以开孔长度作为特征长度，计算对应的St值见表 4。

图 9(Fig. 9)

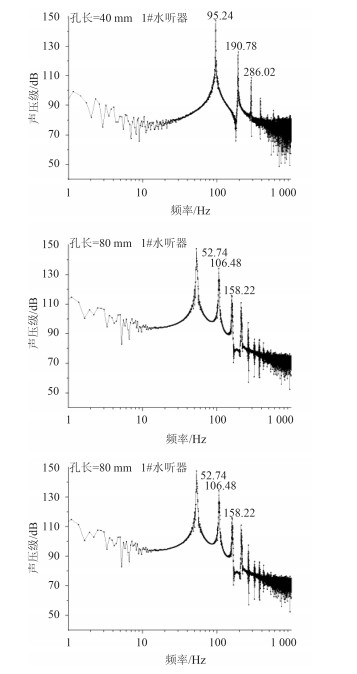
图 9 简化模型频谱图 Fig. 9 Spectrum map of simplified model

表 4(Tab. 4)

表 4 各简化开孔模型流噪声特征频率Tab. 4 Theeigenfrequency of each simplified model 孔长/mm f1/Hz 对应St f2/Hz 对应St f3/Hz 对应St 20 179.35 0.448 359.04 0.898 538.23 1.346 40 95.24 0.476 190.78 0.954 286.02 1.430 80 52.74 0.527 105.48 1.055 158.22 1.582

表 4 各简化开孔模型流噪声特征频率 Tab. 4 Theeigenfrequency of each simplified model

表 4中的结果较好地验证了上节关于特征频率的推断。图 10显示了开孔长度为40 mm时简化模型的局部压力随时间变化的云图，具有一定代表性。

从图 10中可清晰地看到开孔间形成的涡旋及表面压力脉动，从侧面为上节结论提供支撑。

图 10(Fig. 10)

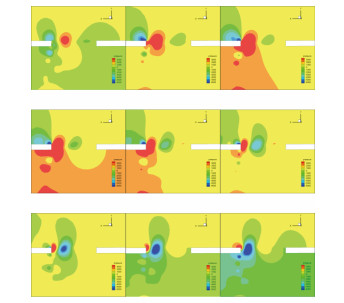
图 10 开孔局部压力时历云图 Fig. 10 Local pressure history contour

本文以水下航行体的水舱开孔作为研究对象，保持开孔面积不变，设置系列长宽比模型进行计算分析，定流场计算结果与试验值吻合良好，在此基础上进行声场计算，得出以下结论：

1）艇体水舱开孔模型的特征频率和水舱的长度无关，与水舱表面开孔在来流方向上的距离有关，而半经验公式在预测水舱开孔噪声时有一定局限性；

2）在开孔水舱流噪声中，由外部流撞击孔壁产生的涡脱落以及在孔壁表面产生的压力脉动是主要成分，而内部水舱中的涡旋强度较低、脉动压力幅值较小，占次要成分；

3）面积一定而长宽比不同的开孔水舱产生的流噪声水平不尽相同，在长宽比小于1时，噪声相对较小，其中在0~0.5区间内，流噪声水平对开孔长宽比较为敏感；

本文所采用的数值方法能获得较为准确地获取水舱开孔模型的声场信息，后续将选取其他设计参数进行系列计算分析，而依据本文模型的声学试验是下一步工作的关键。