2. 高新船舶与深海开发装备协同创新中心, 上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
由于船舶所受载荷的随机性与复杂性,导致结构的破坏形式有很大的不确定性,需要考虑一系列的结构强度问题。传统的许用应力准则已经无法真正考核船体的极限承载能力,而表征结构极限状态的极限强度逐步成为船舶设计与强度分析的一项重要内容。对于具有双舷侧、双层底结构的集装箱船,其船体可以视为“封闭型”的薄壁结构,承担起船舶航行过程中波浪和货物分布所引起的扭转载荷。作为集装箱船极限强度的重要方面,扭转强度会由于结构的损伤而降低,进而导致船体极限承载能力的削弱,甚至发生结构的崩塌破坏。由于局部应力集中或疲劳载荷所导致的裂纹作为船舶结构最重要的损伤类型之一,会破坏船舶结构的完整性,降低船体的极限强度。为了防止不合理的设计及灾难性的破坏,对含裂纹损伤结构的剩余扭转极限强度进行准确的评估十分必要。
胡勇等[1]基于有限元分析,研究板和带加筋板格含裂纹损伤后的剩余极限强度,分析各参数的影响,提出较为准确的回归公式。Paik等[2,3]分别基于试验结果以及采用非线性有限元方法研究轴向压缩载荷下含裂纹损伤平板的剩余极限强度,考虑裂纹位置、尺寸及板厚等多个参数的影响。Alinia等[4]研究裂纹参数、板的尺寸、边界条件及材料属性等对含裂纹板极限强度与刚度衰减的影响,认为裂纹长度和方向会改变剪切板的屈曲性能。师桂杰等[5]以裂纹类型、尺寸以及箱型梁壁厚为主要参数,研究裂纹对扭转、轴向压缩、弯曲以及联合作用下开口箱型梁极限强度的影响。Kim等[6]研究了弯扭联合载荷对矩形截面梁极限强度影响的耦合作用,考虑箱型梁尺寸、材料屈服强度的影响,并计入剪切应力的影响,讨论了弯曲、剪切与扭转的相互作用关系。
本文以含裂纹损伤的箱型梁结构为例,以裂纹尺寸为主要参数,改变裂纹的形式及分布特征,利用非线性有限元软件Abaqus进行了一系列的弹塑性大变形分析,研究箱型梁在扭转载荷下的剩余极限强度。在净截面屈服理论的基础上,通过考虑结构特征及裂纹分布的差异性,考察承受扭转载荷作用下含裂纹损伤箱型梁的应力分布规律,提出评估裂纹影响的剩余极限强度简化计算公式,数值计算结果验证所提出公式的准确性。
1 箱型梁基本模型本文主要研究扭转载荷下特定尺寸裂纹损伤在不同分布特征下对箱型梁极限强度的影响,不考虑裂纹的扩展。为了方便分析,假设裂纹为贯穿钢板上下表面的穿透裂纹,裂纹形式包括中心裂纹与边缘裂纹,不考虑初始缺陷及残余应力的影响。考虑到存在裂纹闭合的可能性时,通常需要在裂纹上下表面设置接触单元进行模拟,但这种闭合又会受到初始缺陷与侧向载荷的影响。而Paik[7]通过比较不同裂纹宽度的结果指出,当裂纹宽度取较大时,结构将在裂纹发生闭合前达到极限状态,得到的结果是含裂纹结构剩余极限强度的下限。本文采用这种方法研究裂纹对箱型梁剩余扭转极限强度的影响。
箱型梁采用横框架加强的延长段形式,两端施加简支约束,加载相应的扭矩。基于Abaqus非线性有限元分析软件,考虑材料非线性与几何非线性,采用Riks弧长法分析模型的极限强度,追踪模型失效破坏的完整过程,可以得到明显下降段的失效曲线以及准确的极限强度值。网格采用四节点、减缩积分的S4R单元,可以避免体积自锁问题,考虑薄膜应变与任意的大转动,适合薄壁结构的有限元分析[8]。
箱型梁的长度取为2a=2 000 mm,宽度为b=1 000 mm,考虑了不同板厚可能存在的影响。假定材料为理想弹塑性,不考虑材料硬化的影响。弹性模量E=206 GPa,泊松比μ=0.3,屈服强度σY=352.8 MPa。通过改变裂纹的分布与尺寸,研究2种裂纹形式下裂纹损伤对扭转极限强度的影响。
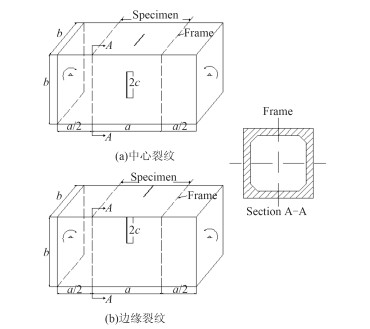
|
图 1 含不同形式裂纹损伤的箱型梁模型 Fig. 1 Box girder model with different forms of crack damage |
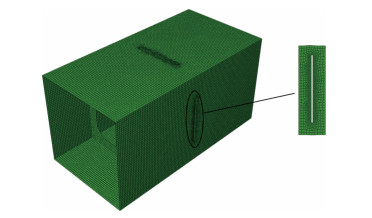
|
图 2 含中心裂纹损伤的箱型梁有限元模型及裂纹区域的局部网格细化 Fig. 2 Finite element meshing of cracked box girder and local mesh refinement |
基于净截面屈服理论,考虑裂纹所引起的横截面积折减,Paik等[7]对含裂纹四边简支板进行了试验与分析,提出了含裂纹平板的拉伸与压缩极限强度计算公式:
| $ \frac{{{\sigma _u}}}{{{\sigma _{u0}}}}=\frac{{{A_c}}}{{{A_0}}}\text{。} $ | (1) |
式中:σu0,σu分别为达到极限状态时,完整板与含裂纹板的正应力;A0,Ac分别为板的初始横截面积与考虑裂纹后的剩余横截面积。
考虑到载荷的差异性以及实际承载状态的复杂性,净截面屈服理论不再完全适用于含裂纹箱型梁扭转极限强度的预测。特别是由于结构特征的差别,箱型梁上裂纹的分布特征相较平板结构更为复杂,对扭转极限强度的影响存在相互作用关系。因此,有必要对裂纹所引起的折减面积引入一个系数,表征实际承载状态下裂纹对扭转极限强度的衰减程度。
3 裂纹对箱型梁扭转极限强度的影响在两端独立节点施加扭矩,箱型梁发生扭转变形,端部的平均扭转应力定义为:
| $ \tau {\rm{=}}\frac{{T}}{{2At}}\text{。} $ | (2) |
式中:T为箱型梁端部的扭矩;A为箱型梁的截面面积;t为箱型梁的壁厚。
为了考察箱型梁结构不同裂纹分布特征的影响,这里以中心裂纹为例,选取板厚t=10 mm的结果进行分析。如图 3和图 4所示,扭转载荷作用下箱型梁不同裂纹分布特征对扭转极限强度的影响有很大差别。其中,一边存在裂纹与两对边存在裂纹所引起的扭转极限强度衰减程度十分接近,且在裂纹长度2c/b > 0.3时裂纹会明显降低扭转极限强度。而两相邻边存在裂纹、三边存在裂纹与四边存在裂纹这3种裂纹情况在裂纹尺寸相同时所造成的扭转极限强度衰减基本相同,在裂纹长度2c/b=0.1时几乎没有影响,当2c/b > 0.2时便会对扭转极限强度产生明显的降低影响。经过有限元验证,对于边缘裂纹,这种裂纹分布特征的影响基本一致,相邻边同时存在裂纹情况下结构的扭转极限强度已经出现很大的衰减。
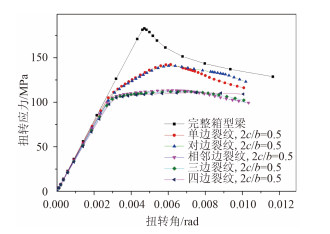
|
图 3 不同中心裂纹分布下的扭转极限强度,t=10 mm,2c/b=0.5. Fig. 3 The ultimate torsional strength of center-cracked box with crack size 2c/b=0.5,corresponding to diverse crack distributions,t=10 mm. |
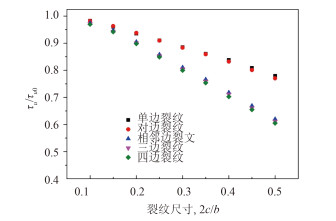
|
图 4 中心裂纹分布特征对扭转极限强度的影响,t=10 mm. Fig. 4 Effect of center-crack distributions on the ultimate torsional strength of cracked box,t=10 mm. |
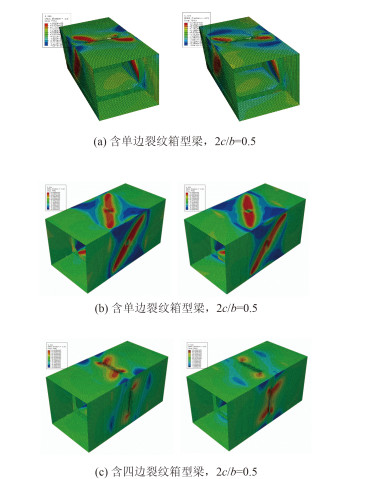
这说明箱型梁对边存在的裂纹相比单边裂纹不会导致更大的扭转极限强度衰减,但当相邻边同时存在裂纹时便会对极限强度产生很大的衰减,衰减的程度基本与四边同时存在相同裂纹的情况相近。不同裂纹分布与尺寸下的箱型梁薄膜应力分布如图 5所示,当裂纹长度为2c/b=0.1时,薄膜应力的分布与完整箱型梁基本一致,应力的连续性不会受到破坏,因此极限强度降低并不明显;而当裂纹长度达到2c/b=0.5时,沿对角线处的载荷已经无法连续地传递,因此对扭转极限强度的降低十分显著。
|
图 5 达到扭转极限状态时箱型梁的薄膜应力分布 Fig. 5 Membrane stress distribution at the ultimate limit state under torque |
相比两相邻边裂纹或四边裂纹,单边裂纹下相邻无裂纹边板格的应力区域呈对角线分布,有很好的连续性,仍能够有效地传递载荷,因此对极限强度的降低较小;同时可以看到,单边裂纹改变了其对边无裂纹板格的应力分布状态,使其对整体的承载能力贡献减小,因而当对边板格也存在裂纹时对扭转极限强度进一步的降低作用已经很小。而相邻边裂纹则会很大程度上破坏箱型梁板格的连续性,同时使得其余两边无裂纹板格对整体承载能力的贡献减小,对极限强度的衰减最严重。因此可以认为,多边裂纹对扭转极限强度的影响取决于其中主要的相邻边裂纹所导致的极限强度衰减。
为了考虑板厚可能存在的影响,对不同板厚箱型梁结构的剩余扭转极限强度进行分析与比较。数值计算结果表明,研究裂纹对扭转极限强度的衰减时不同板厚的结果差别很小,说明两者在扭转载荷下的耦合关系并不显著,扭转极限强度的衰减程度主要取决于裂纹的分布特征。扭转载荷下裂纹对极限强度的影响有别于弯曲、拉压载荷下有效承载面积的折减,对扭转刚度与强度造成的衰减往往更为显著。对于扭转极限强度,师桂杰[8]验证了净截面理论对预测含四边同时存在裂纹损伤箱型梁剩余扭转极限强度的有效性,但没有考虑不同裂纹分布特征的影响。考虑到受环向均匀分布的扭转载荷作用下箱型梁各板承扭作用相同,引入系数α表征各边裂纹对箱型梁扭转极限强度的降低影响,认为单边裂纹对扭转极限强度所造成的影响为:
| $ \frac{{{\tau _u}}}{{{\tau _{u0}}}}=\frac{{(4b-\alpha \cdot 2c)t}}{{4bt}}=1-\frac{\alpha }{4} \cdot \frac{{2c}}{b} $ | (3) |
假设箱型梁结构一边含有2c/b=0.84的裂纹,相邻边则含有长度为2c0的中心裂纹,根据文献[5]提出的预测单一载荷下含裂纹损伤开口箱型梁的剩余极限强度公式可以近似得到:
| $ \displaystyle\frac{{1-\displaystyle\frac{\alpha }{4} \times(0.84+\frac{{2{c_0}}}{b})}}{{1-\displaystyle\frac{\alpha }{4} \times 0.84}}=1-\frac{{2.37}}{{3.16}} \times \frac{{2{c_0}}}{b}\text{。} $ | (4) |
因此可得:α=1.84。显然,大尺寸的裂纹虽然破坏了结构的连续性,但相比大开口对极限强度的降低影响仍较小,因此得到的α值合理且偏保守。而由于四边分布裂纹对扭转极限强度的影响取决于其中的相邻边裂纹,因此只需考虑其主要相邻边裂纹所造成的有效面积折减。基于此,本文提出含四边裂纹损伤箱型梁的剩余扭转极限强度公式:
| $ \frac{{{\tau _u}}}{{{\tau _{u0}}}}=1-\frac{\alpha }{4} \cdot \frac{{2c}}{b} \times 2=1-\frac{\alpha }{2} \cdot \frac{{2c}}{b} \text{。} $ | (5) |
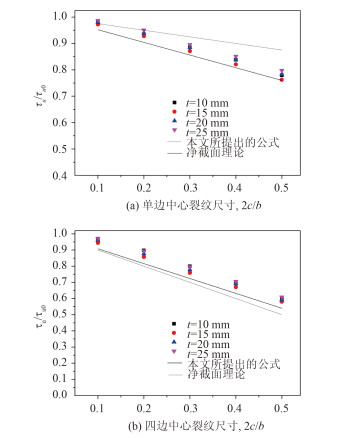
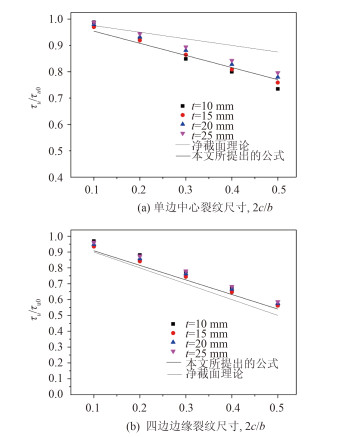
中心裂纹损伤与边缘裂纹损伤对箱型梁结构扭转极限强度的影响如图 6与图 7所示。从有限元结果可以看到,相较中心裂纹,相同尺寸的边缘裂纹损伤由于影响到不同板格间的载荷传递,对扭转极限强度的降低作用更为显著,这从边缘裂纹损伤下结构应力分布状态更为明显的变化同样可以看出。净截面理论(α=1)虽然适用于四边同时存在裂纹损伤的情况,但显然不适用于预测单边裂纹损伤对扭转极限强度的降低影响,这是因为箱型梁结构中不同板格分布的裂纹之间并不独立,存在相互作用的关系。通过引入系数α=1.84,式(3)可以很好地估计单边中心裂纹或边缘裂纹损伤的影响,反映扭转极限强度随裂纹尺寸增加的衰减趋势。其中,单边边缘裂纹损伤的计算结果关于板厚在预测公式附近呈现了较大的离散性,但由于本文并不考虑裂纹闭合可能导致的扭转极限强度偏高,得到的有限元结果是剩余极限强度的下限,因而可以认为所提出的公式仍准确且保守。在此基础上,相较净截面理论公式,式(5)同样能够更有效地估计相邻边或四边裂纹损伤对扭转极限强度的降低影响,验证了公式的合理性。
|
图 6 中心裂纹对箱型梁剩余扭转极限强度的影响 Fig. 6 Effect of center-crack on the residual ultimate torsional strength of cracked box |
|
图 7 边缘裂纹对箱型梁剩余扭转极限强度的影响 Fig. 7 Effect of edge-crack on the residual ultimate torsional strength of cracked box |
基于有限元分析,本文针对箱型梁结构的裂纹损伤问题,研究裂纹对箱型梁剩余扭转极限强度的影响,得到以下结论:
1)通过考虑扭转载荷下箱型梁裂纹尺寸与分布特征的影响,引入系数评估裂纹的影响,提出相应的剩余极限强度简化计算公式(3)与公式(5),通过与不同裂纹形式与特征的数值计算结果相比较,可以分别有效地预测含单边裂纹与四边裂纹损伤箱型梁的扭转极限强度,具有较好的准确度。
2)基于净截面屈服的预测公式虽然能较好地评估四边裂纹损伤对箱型梁扭转极限强度的影响,但对单边或双边裂纹则并不适用,这是因为箱型梁结构中裂纹对扭转刚度及强度造成的降低影响往往更为显著,且不同板格分布的裂纹之间存在相互作用关系。
3)研究裂纹损伤对扭转极限强度的衰减时板厚的影响很小,说明两者在扭转载荷下的耦合关系并不显著,扭转极限强度的衰减主要取决于裂纹的分布特征与尺寸。
4)在裂纹长度2c/b≤0.1时,无论何种形式的裂纹,箱型梁的扭转极限强度降低很小;裂纹长度2c/b≥0.3时,箱型梁板格上载荷传递的连续性已经受到较大的破坏,因而极限强度的降低程度较为显著。
5)与中心裂纹相比,相同裂纹尺寸的边缘裂纹对箱型梁扭转极限强度的衰减相对更为显著,这是因为边缘裂纹影响到不同板格间的载荷传递,更大程度上改变了结构的应力分布状态,因而对结构承载能力的降低作用更为明显。
6)对于受扭转载荷作用的含裂纹损伤箱型梁结构,单边裂纹改变了其对边无裂纹板格的应力分布状态,当对边板格也存在裂纹时对扭转极限强度进一步的降低作用已经很小;而相邻边裂纹的存在同样使得其余两边无裂纹板格对整体承载能力的贡献减小,对极限强度的衰减最严重。
| [1] |
胡勇, 崔维成. 具有裂纹缺陷的板和加筋板格在联合载荷作用下的剩余极限强度[J]. 船舶力学, 2003, 7(1):63-78. HU Yong, CUI Wei-cheng. Residual ultimate strength of cracked plates and stiffened panels under combined loading[J]. Journal of Ship Mechanics, 2003, 7(1):63-78. |
| [2] | PAIK J K. Residual ultimate strength of steel plates with longitudinal cracks under axial compression-nonlinear finite element method investigations[J]. Ocean Engineering, 2009, 36(3/4):266-276. |
| [3] | PAIK J K. Residual ultimate strength of steel plates with longitudinal cracks under axial compression-experiments[J]. Ocean Engineering, 2008, 35(17/18):1775-1783. |
| [4] | ALINIA M M, HOSSEINZADEH S A A, HABASHI H R. Influence of central cracks on buckling and post-buckling behaviour of shear panels[J]. Thin-walled Structures, 2007, 45(4):422-431. |
| [5] | SHI G J, WANG D Y. Residual ultimate strength of open box girders with cracked damage[J]. Ocean Engineering, 2012, 43:90-101. |
| [6] | KIM K, YOO C H. Ultimate strengths of steel rectangular box beams subjected to combined action of bending and torsion[J]. Engineering Structures, 2008, 30(6):1677-1687. |
| [7] | PAIK J K, KUMAR Y V S, LEE J M. Ultimate strength of cracked plate elements under axial compression or tension[J]. Thin-walled Structures, 2005, 43(2):237-272. |
| [8] | SHI G J, WANG D Y. Residual ultimate strength of cracked box girders under torsional loading[J]. Ocean Engineering, 2012, 43:102-112. |
 2016, Vol. 38
2016, Vol. 38
