2. 中国人民解放军92267部队, 山东 青岛 266102
2. No. 92267 Unit of PLA, Qingdao 266102, China
深海潜标是一种海洋环境监测平台,可根据需求搭载不同的监测设备和仪器,这些设备和仪器对潜标姿态有不同的要求,必须进行姿态控制。目前国内外多采用单点绷紧型系留系统保持潜标竖直向上姿态,该方法加装浮子较多,体积大,不能任意调整姿态[1];此后,Fang,Feng 和 Allen,Huang等[2, 3, 4]对带缆遥控潜水器水动力特性的研究为主动姿态控制打下基础。葛德宏等[5, 6]研究了潜标加装尾翼保证在单垂直面倾斜时的主动姿态控制方法,以满足某仪器特种条件下的使用要求。本文考虑不加装尾翼的潜标在水平流的作用下产生纵倾和横倾时的主动姿态控制方法。以潜标与缆索的水动力数学模型为基础[7],在潜标内部安装姿态传感器测量潜标纵横倾,通过解耦,基于输入输出线性化设计 2 个垂直面的姿态控制器,并分别控制 2 个方向的螺旋桨,实现多螺旋桨推力姿态控制。仿真结果表明,多方向的推力可以将潜标姿态跟踪到参考姿态,具有一定的实践指导意义和理论参考价值。
1 数学模型假设海流为速度大小和方向是单一的定常海流,且海流只能在同一水平面流动,不同流层的水流互不关联。
1.1 潜标六自由度运动方程运动模型的建立需要基于一定的坐标系,这 3 个坐标系分别为:惯性坐标系 OXYZ,潜标主体坐标系 oxyz,缆索局部坐标系 o′tnb,具体定义参见文献[5]。
潜标的水动力特性由通用的潜艇六自由度运动方程来描述[8],暂不考虑水流、波浪对系统水动力的影响,即运动方程中的各速度项均为潜标各构件的绝对速度。在潜标主体坐标系下,该方程可以表述为:
| $ \begin{array}{*{20}{l}} {m[\dot u - vr + wq - {x_G}({q^2} + {r^2}) + }\\ {\quad \quad \quad {y_G}(pq - \dot r) + {z_G}(pr + \dot q)] = X,}\\ {m[\dot v + ur - wp + {x_G}(pq + \dot r) - }\\ {\quad \quad \quad {y_G}({p^2} + {r^2}) + {z_G}(qr - \dot p)] = Y,}\\ {m[\dot w - uq + vp + {x_G}(pr - \dot q) + }\\ {\quad \quad \quad {y_G}(qr + \dot p) - {z_G}({p^2} + {q^2})] = Z,}\\ {{I_x}\dot p + ({I_z} - {I_y})qr + {I_{xy}}(pr - \dot q) - }\\ {\quad \quad \quad {I_{yz}}({q^2} - {r^2}) - {I_{xz}}(pq + \dot r) + }\\ {\quad \quad \quad m[{y_G}(\dot w - uq + vp) - }\\ {\quad \quad \quad {z_G}(\dot v + ur - wp)] = K,}\\ {{I_y}\dot q + ({I_x} - {I_z})pr - {I_{xy}}(qr + \dot p) + }\\ {\quad \quad \quad {I_{yz}}(pq - \dot r) + {I_{xz}}({p^2} - {r^2}) - }\\ {\quad \quad \quad m[{x_G}(\dot w - uq + vp) - }\\ {\quad \quad \quad {z_G}(\dot u - vr + wq)] = M,}\\ {{I_z}\dot r + ({I_y} - {I_x})pq - {I_{xy}}({p^2} - {q^2}) - }\\ {\quad \quad \quad {I_{yz}}(pr + \dot q) + {I_{xz}}(qr - \dot p) + }\\ {\quad \quad \quad m[{x_G}(\dot v + ur - wp) - }\\ {\quad \quad \quad {y_G}(\dot u - vr + wq)] = N.} \end{array} $ | (1) |
式中:m 为潜标质量;(xG,yG,zG)为潜标主体坐标系下的重心坐标;Ix,Iy 和 Iz 为潜标的质量惯性矩;Ixy,Iyz 和 Ixz 为潜标的交叉质量惯性矩;[u,v,w]T 和 [p,q,r]T 为潜标的三维线速度和角速度;$ {[\dot u,\dot v,\dot w]^{\rm{T}}} $ 和 $ {[\dot p,\dot q,\dot r]^{\rm{T}}} $ 为潜标的三维线加速度和角加速度;右端项为作用在潜标上的外力 $ {{{F}}_0} = {[X,Y,Z]^{\rm T}} $ 和外力矩 $ {{{M}}_0} = {[K,M,N]^{\rm T}} $。
假设由静水回复力、系缆张力、水动力及其相应的力矩组成,有
| $ \begin{equation} \begin{array}{l} {{{F}}_0} = {{{F}}_W} + {{{F}}_T} + {{{F}}_H},\\ {{{M}}_0} = {{{M}}_W} + {{{M}}_T} + {{{M}}_H}\text{。} \end{array} \end{equation} $ | (2) |
式中:下标 W 代表静水回复力;下标 T 代表缆索张力;下标 H 代表作用在潜标上的水动力。
深海潜标工作时主要考虑海流的影响,为讨论海流环境下潜标系统的水动力特性,需要求出海流环境下潜标主体的相对速度和加速度,替换潜标运动方程左边的相应项。
潜标的相对速度为:
| $ \begin{equation} \left\{ \begin{array}{l} {u_r} = u-U\cos \theta \sin \alpha \cos (\psi -\beta ) + \\ \quad\quad U\sin \theta \cos \alpha ,\\ {v_r} = v-U\sin \alpha \sin (\psi -\beta ),\\ {w_r} = w-U\sin \theta \sin \alpha \cos (\psi -\beta )-\\ \quad\quad U\cos \theta \cos \alpha \text{。} \end{array} \right. \end{equation} $ | (3) |
式中:U 为海流速度;α 和 β 分别为流向与 Z 轴及 X 轴的夹角。
由于海流本身不存在转动问题,所以海流没有角速度。将式(3)中的速度项替换潜标运动式(1)中的相应项,即可得到潜标在海流干扰下的运动方程。
式(1)中由浮力和重力产生的静水回复力、流体水动力、缆索张力及力矩计算[4, 9]。
1.2 简化模型潜标运动时是多自由度耦合的非线性运动系统,该模型不适合用于设计姿态控制器,可以用于检验控制策略设计是否合理,控制器的设计应选择避开运动相互耦合的简化模型。在来流使潜标同时产生纵倾和横倾时,通过解耦,将潜标运动化解为在 2 个垂直平面运动的简化模型,并以此来设计控制器。
潜标在来流方向角不为 0° 时产生纵横倾角时,姿态控制需要的外作用力主要为 X、Y 方向的推力和绕 X、Y 轴旋转的力矩,该力和力矩由多螺旋桨旋转产生。设计在潜标主体侧面布置 4 个物理特征相同的螺旋桨(1,2,3,4号螺旋桨),如图 1 所示。在潜标局部坐标系下,1 号螺旋桨产生沿 X 轴反方向的推力及绕 Y 轴的力矩,2 号螺旋桨产生沿 X 轴方向的推力及绕 Y 轴反方向的力矩,3 号螺旋桨产生沿 Y 轴反方向的推力及绕 X 轴反方向的力矩,4 号螺旋桨产生沿 Y 轴方向的推力及绕 X 轴方向的力矩。若控制力足够的话,则控制系统任一时刻只需要 2 个螺旋桨工作,且单个螺旋桨只正转,不反转,以避免螺旋桨反转造成的偏转现象。
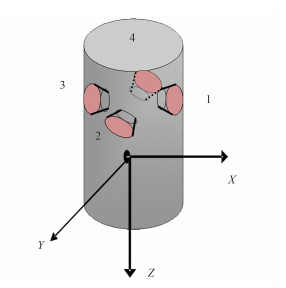
|
图 1 螺旋桨布置 Fig. 1 The location of four propellers |
经前期运动仿真可知,在以上坐标系下具有尾鳍的潜标主要在垂直面上(OXZ)运动[4],则控制器设计只考虑 u,w,q,θ 四个变量,则式(1)简化后联立 θ 相关方程为:
| $ \begin{equation} \begin{array}{l} m(\dot u + wq-{x_G}{q^2} + {z_G}\dot q) = X ,\\ m(\dot w-uq-{x_G}\dot q-{z_G}{q^2}) = Z ,\\ {I_y}\dot q-m[{x_G}(\dot w-uq)-{z_G}(\dot u + wq)] = M ,\\ \dot \theta = q\text{。} \end{array} \end{equation} $ | (4) |
设 $ \xi = {[u\;\;w\;\;q\;\;\theta]^{\mathop{\rm T}\nolimits} } $,$ z = \theta $,uc 为控制输入,在此处为沿 X 轴反方向的推力,则
| $ \dot \xi = M_R^{ - 1}{f_1}(\xi ) + M_R^{ - 1}{g_1}(\xi ){u_c} = f(\xi ) + g(\xi ){u_c}; $ | (5a) |
| $ z = h(\xi ). $ | (5b) |
其中:
| $ \begin{array}{l} M_R^{ - 1} = {\left[ {\begin{array}{*{20}{l}} {\;\;\;m\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;m{Z_G}\;\;\;\;0\;}\\ {\;\;\;0\;\;\;\;\;\;\;\;\;\;m\;\;\;\;\;\;\; - m{X_G}\;\;\;0}\\ { - m{Z_G}\;\;\; - m{X_G}\;\;\;\;\;\;{I_y}\;\;\;\;\;\;\;0}\\ {\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;1\;} \end{array}} \right]^{ - 1}},\\ {f_1}(\xi ) = \left[ {\begin{array}{*{20}{l}} {\;\;\;X - mwq + m{X_G}{q^2}\;}\\ {\;\;\;Z + muq + m{Z_G}{q^2}}\\ {M - m{X_G}uq - m{Z_G}wq}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;q\;} \end{array}} \right],\\ {g_1}(\xi ) = {\left[ { - 1\;\;0\;\;{Z_c}\;\;0} \right]^{\rm{T}}},{u_c} = {F_{cX}},h(\xi ) = \theta . \end{array} $ |
当来流方向不为 0,即不与 X 轴同向时,可将潜标运动看做在 OXZ 和 OYZ 平面 2 个垂直面的运动。同上,在 OYZ 平面运动控制器设计只考虑 v,w,p,Φ 4 个变量,则六自由度方程简化后联立 Φ 相关方程为:
| $ \begin{equation} \begin{array}{l} m(\dot v-wp-{y_G}{p^2}-{z_G}\dot p) = Y,\\ m(\dot w + vp + {y_G}\dot p-{z_G}{p^2}) = Z,\\ {I_x}\dot p + m[{y_G}(\dot w + vp)-{z_G}(\dot v-wp)] = K,\\ \dot \phi = p\text{。} \end{array} \end{equation} $ | (6) |
该方程同样可用相似的矩阵形式表达。
2 姿态控制系统设计考察下列 SISO 非线性系统:
| $ \begin{equation} \left\{ \begin{array}{l} \dot \xi = f(\xi ) + g(\xi ){u_c},\\[3pt] z = h(\xi )\text{。} \end{array} \right. \end{equation} $ | (7) |
式中:$ \xi \in \Omega \subset {R^n} $;f,g 为 Rn 上的矢量场;h 为光滑非线性函数;z 为系统输出;uc 为系统输入。所谓输入输出线性化,就是要获得输入输出之间的一个线性微分关系。
得到线性输入输出关系的基本方法就是简单地对输出函数 z 进行微分,以便得到与输入的直接关系
| $ \begin{equation} \dot z = \nabla h(f + g{u_c}) = {L_f}h(\xi ) + {L_g}h(\xi ){u_c}\text{。} \end{equation} $ | (8) |
在区域 Ω 内,对于所有的 ξ ,如果李导数 $ {L_g}h(\xi ) = 0 $,可以对 $ \dot z $ 继续进行微分,直至 $ {L_g}L_f^{\gamma -1}h(\xi ) \ne 0 $ ,然后通过状态反馈控制律[10]
| $ \begin{equation} {u_c} = \frac{1}{{{L_g}L_f^{\gamma -1}h}}(-L_f^\gamma h + {\upsilon _c}), \end{equation} $ | (9) |
可得到输入 $ {\upsilon _c} $ 到输出 z 之间的高阶线性系统
| $ \begin{equation} {z^{(\gamma )}} = {\upsilon _c}\text{。} \end{equation} $ | (10) |
为了使输入 uc 出现,需要对 z 进行微分的次数 γ 称为系统的相对阶。
依据以上方法,为得到线性输入输出关系,对式(5b)中输出函数 z 进行了 2 次微分,有
| $ \begin{equation} \begin{split} \begin{aligned} \ddot z = & {[{{M}}_R^{-1}{f_1}(\xi ) + {\mathop{\rm M}\nolimits} _R^{-1}{g_1}(\xi ){u_c}]_{31}} =\\ & [-{({\mathop{ M}\nolimits} _R^{-1})_{31}} + {({\mathop{ M}\nolimits} _R^{-1})_{33}}{{ Z}_c}]{u_c} + f(\xi )\text{。} \end{aligned} \end{split} \end{equation} $ | (11) |
其中:
| $ \begin{equation*} \begin{aligned} f(\xi ) = & {({\mathop{ M}\nolimits} _R^{-1})_{31}}(X-mwq + m{X_G}{q^2}) + \\ & {({\mathop{ M}\nolimits} _R^{-1})_{32}}(Z + muq + m{Z_G}{q^2}) + {({\mathop{ M}\nolimits} _R^{-1})_{33}} \times \\ & ({ M}-m{X_G}uq-m{Z_G}wq) + {({\mathop{ M}\nolimits} _R^{-1})_{34}}q \text{。} \end{aligned} \end{equation*} $ |
此时,$ L_f^2h(\xi ) = f(\xi ) $,选定重心为原点,控制力作用在浮心上($ {Z_c} \ne 0 $),则 $ {({\mathop{ M}\nolimits} _R^{-1})_{31}} = 0 $;$ {({\mathop{ M}\nolimits} _R^{-1})_{33}} \ne 0 $,则 $ {L_g}L_f^{2-1}h(\xi ) = -{({\mathop{ M}\nolimits} _R^{-1})_{31}} + {({\mathop{ M}\nolimits} _R^{-1})_{33}}{Z_c} \ne 0 $,输入控制 uc 被导出,因此可以看出,系统的相对阶 γ 为 2。
根据式(9)取状态反馈控制律
| $ \begin{equation} \begin{array}{l} {u_c} = \displaystyle\frac{1}{{{L_g}L_f^{2-1}h}}(-L_f^2h + {\upsilon _c}) = \\[10pt] \displaystyle\frac{1}{{-{{({\mathop{ M}\nolimits} _R^{-1})}_{31}} + {{({\mathop{ M}\nolimits} _R^{-1})}_{33}}{{ Z}_c}}}[-f(\xi ) + {\upsilon _c}]\text{。} \end{array} \end{equation} $ | (12) |
代入式(11)得线性 2 阶微分方程
| $ \begin{equation} \ddot z = {\upsilon _c}\text{。} \end{equation} $ | (13) |
观察上式,如果取
| $ \begin{equation} {\upsilon _c} = -{k_1}z-{k_2}\dot z, \end{equation} $ | (14) |
代入式(13),可得到闭环系统
| $ \begin{equation} \ddot z + {k_2}\dot z + {k_1}z = 0\text{。} \end{equation} $ | (15) |
式中 k1,k2 为大于 0 的实数,由设计者选定。
将式(14)代入式(12),可得控制律为
| $ \begin{equation} \begin{array}{*{20}{l}} {{u_c} = \displaystyle\frac{1}{{{L_g}L_f^{2-1}h}}(-L_f^2h + {\upsilon _c})}= \\[10pt] \quad\,\,\,\,{ \displaystyle\frac{1}{{-{{({\rm{M}}_R^{-1})}_{31}} + {{({\rm{M}}_R^{-1})}_{33}}{Z_c}}} \cdot } {[-f(\xi )-{k_1}z-{k_2}\dot z]}\text{。} \end{array} \end{equation} $ | (16) |
式(16)即为所求的 X 方向姿态控制律。
综合可得,化简后 X 轴方向推进螺旋桨提供的推力:
| $ \begin{equation} \begin{array}{l} {u_{cx}} = \displaystyle\frac{{{I_y}}}{{{Z_c}}}[\!-\! {k_1}\theta \!-\! {k_2}q \!+\! \frac{1}{{{I_y}}} (M \!-\! m{X_G}uq \!-\! m{Z_G}wq)]\\[10pt] \quad\,= \displaystyle\frac{{{I_y}}}{{{Z_c}}}(-{k_1}\theta -{k_2}q + \frac{M}{{{I_y}}})\text{;} \end{array} \end{equation} $ | (17) |
Y 轴方向推进螺旋桨提供的推力:
| $ \begin{equation} \begin{array}{l} {u_{cy}} = \displaystyle\frac{{{I_x}}}{{{Z_c}}}[\!-\! {k_3}\phi \!-\! {k_4}p \!+\! \frac{1}{{{I_x}}} (K \!-\! m{Y_G}vp \!-\! m{Z_G}wp)]\\[10pt] \quad\,= \displaystyle\frac{{{I_x}}}{{{Z_c}}}(-{k_3}\phi -{k_4}p + \frac{K}{{{I_x}}})\text{。} \end{array} \end{equation} $ | (18) |
仿真条件如下:潜标长 7.6 m,正浮力为 160 N,以重心为原点,流体力与控制力作用点(0,0,-1.15);缆索长 30 m,直径 4 mm;潜标阻力系数 CD 为 1.2,缆索法向阻力系数为 0.9,切向阻力系数为 0.02。潜标的初始条件为在静水中竖直向上状态,海流速度为 2 kn。控制周期 0.5 s,最大控制力 1000 N,最小控制力 0 N,X、Y 方向控制器的控制参数 k1 = 1,k2 = 3,k3 = 1,k4 = 3。在 120 s 前不控制,潜标运动达到稳态,120 s 后开始控制。
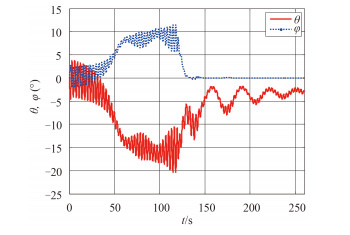
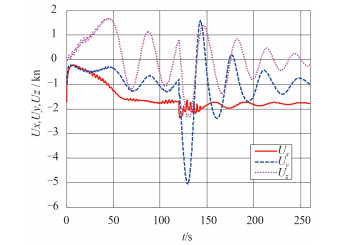
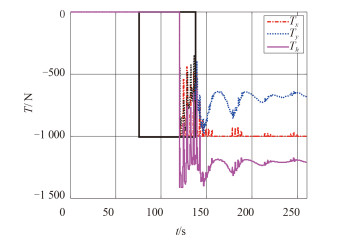
图 2 ~ 图 4 为海流夹角与 X 轴成 30°,Y 轴成 60° 时,潜标在海流中运动及控制后运动的动态变化情况。
|
图 2 潜标纵倾、横倾角动态变化 Fig. 2 Dynamic change of submerged buoy pitch and roll |
|
图 3 潜标在 X,Y,Z 轴方向相对速度动态变化 Fig. 3 Relative speed change of submerged buoy along three axis |
|
图 4 潜标在 X,Y 轴方向控制力及其合力动态变化 Fig. 4 Force change of submerged buoy along X,Y axis |
图 2 为潜标纵倾和横倾角变化历程仿真结果,可见在 2 kn 海流作用在潜标上,由于海流流向与 X,Y 轴存在不同夹角,因此作用到 X 轴和 Y 轴方向的水动力也不同,虽然均呈现出从竖直向上的初始状态顺流倾斜角中心值逐渐增大的趋势,但稳态值不同,纵倾角约为 15°,横倾角约为 9°。120 s 施加推力控制,经控制纵倾角小于 5°,横倾角接近 0°,说明控制器的设计是切实有效的。分析结果图 2 中潜标倾角具有周期振荡特性,分析认为是潜标在海流阻尼力和自身扶正力矩作用下的动态响应结果。图 3 为潜标在 X,Y,Z 轴方向的相对速度动态变化曲线。由图可见,在 2 kn 海流的阻尼力作用下,0 ~ 120 s 时潜标沿 X,Y 轴方向相对速度值从与流速分别在该方向的分量相等开始变化,达到基本稳态时,其相对速度恢复到流速分量值,仿真结果符合常识,经控制达到稳态后,相对速度也基本达到流速分量值。图 4 分别为潜标在 X 轴、Y 轴方向的控制力与控制合力曲线,控制合力的稳态值与流体作用力相当。
在海流方向与 X 轴成 45°,Y 轴成 45° 时,潜标在流中运动及控制后运动的动态变化情况,如图 5 ~ 图 7 所示。
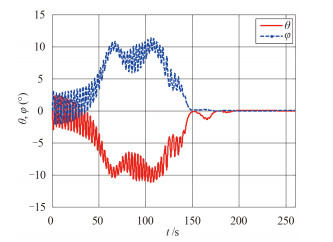
|
图 5 潜标纵倾、横倾角动态变化 Fig. 5 Dynamic change of submerged buoy pitch and roll |
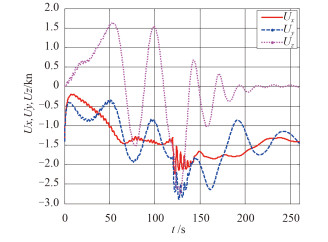
|
图 6 潜标在 X,Y,Z 轴方向相对速度动态变化 Fig. 6 Relative speed change of submerged buoy along three axis |
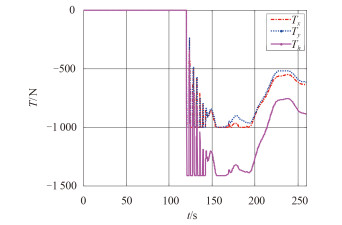
|
图 7 潜标在 X,Y 轴方向控制力及其合力动态变化 Fig. 7 Force change of submerged buoy along X,Y axis |
图 5 为潜标纵倾和横倾角变化历程仿真结果,可见在 2 kn 海流作用在潜标上,由于海流流向与 X、Y 轴存在 45° 夹角,因此作用到 X 轴和 Y 轴方向的水动力大小相同,因此稳态值也接近相同,约为 10°,经控制纵倾角、横倾角接近 0°,说明控制器的设计是切实有效的。图 6 曲线图分析可得出与图 3 分析相似的结果。
综上所述,采用相同的控制参数,对不同夹角的海流作用下潜标进行姿态控制的仿真表明,控制器设计有效。
4 结 语本文通过对潜标空间运动的非线性数学模型进行解耦化简,得到适合于控制器设计的 2 个垂直面运动简化非线性模型,提出了一种基于输入输出线性化的状态反馈姿态控制律,编制了 Matlab 计算机程序。较为理想的仿真结果表明,该控制律能够将处于不同海流流向下的深海潜标的姿态控制到参考姿态,具有一定的实践指导意义和理论参考价值。以上设计的控制器,最终的控制输出量为螺旋桨在各自由度上的推力和力矩。这些值由系统中所有参与推进的螺旋桨旋转产生的总推力和总力矩来贡献。选定螺旋桨型号后,通过已知参数,可将控制推力转化为转速。
| [1] | CHEN X H. Studies on dynamic interaction between deep-water floating structures and their mooring/tendon systems[D]. Houston:Texas A & M University, 2002. |
| [2] | FANG M C, HOU C S, LUO H J. On the motions of the underwater remotely operated vehicle with the umbilical cable effect[J]. Ocean Engineering, 2007, 34(8/9):1275-1289. |
| [3] | FENG Z, ALLEN R. Evaluation of the effects of the communication cable on the dynamics of an underwater flight vehicle[J]. Ocean Engineering, 2004, 31(8/9):1019-1035. |
| [4] | HUANG S. Stability analysis of the heave motion of marine cable-body systems[J]. Ocean Engineering, 1999, 26(6):531-546. |
| [5] |
葛德宏, 朱海, 陈建华, 等. 深海潜标系统运动仿真研究[J]. 大连海事大学学报, 2014, 40(1):25-28, 32. GE De-hong, ZHU Hai, CHEN Jian-hua, et al. Motion simulation study of deep-sea submerged buoy system[J]. Journal of Dalian maritime University, 2014, 40(1):25-28, 32. |
| [6] |
葛德宏, 朱海, 陈建华, 等. 基于输入输出线性化的深海潜标姿态控制[J]. 海军工程大学, 2014, 26(5):92-96. GE De-hong, ZHU Hai, CHEN Jian-hua, et al. Attitude control of deep-sea submerged buoy based on input-output linearization[J]. Journal of Naval University of Engineering, 2014, 26(5):92-96. |
| [7] |
葛德宏, 朱海, 蔡鹏, 等. 基于反馈线性化的深海潜标姿态滑模控制[J]. 火力与指挥控制, 2016, 41(1):16-18. GE De-hong, ZHU Hai, CAI Peng, et al. Attitude sliding mode control of deep-sea submerged buoy based on feedback linearization[J]. Fire Control & Command Control, 2016, 41(1):16-18. |
| [8] |
GERTLER M, HAGEN G L. Standard equations of motion for submarine simulation[R]. Technical Report DTMB 2510. Washington, DC:David Taylor Research Center, 1967. |
| [9] |
郁苗. 带缆遥控水下机器人的模糊滑模控制研究[D]. 广州:华南理工大学, 2010. YU Miao. Research on fuzzy sliding mode control of a remotely operated underwater vehicle[D]. Guangzhou:South China University of Technology, 2010. |
| [10] |
周岗, 姚琼荟, 陈永冰, 等. 基于输入输出线性化的船舶全局直线航迹控制[J]. 控制理论与应用, 2007, 24(1):117-121. ZHOU Gang, YAO Qiong-hui, CHEN Yong-bing, et al. Global straight-line tracking control of ships based on input-output linearization[J]. Control Theory & Applications, 2007, 24(1):117-121. |
 2016, Vol. 38
2016, Vol. 38
