2. 中国船舶重工集团公司第七一三研究所, 河南郑州 450015
2. The 713 Research Institute of CSIC, Zhengzhou 450015, China
舰载导弹垂直发射技术具有反应快速、全方位覆盖、装弹量大、武器系统简化、可靠性高、模块化设计、通用性好等优点,近年来在火箭弹、防空导弹和巡航导弹发射系统中得到广泛应用[1, 2, 3, 4, 5, 6, 7, 8]。适配器是导弹、火箭弹垂直发射筒中的重要组成部分,在导弹装入发射筒时,采用预压缩方式装配在导弹与发射筒中的合适位置。适配器一般采用2种以上大阻尼比、超弹性材料层叠而成。
舰载导弹垂直发射时,受到不平衡力作用,弹体会发生横向振动;由于适配器安装在导弹和发射箱内导轨之间,并且是过盈配合,能够避免导弹和发射导轨碰撞,同时适配器为超弹性大阻尼材料能够降低导弹的横向振动。舰载导弹垂直发射过程,导弹-适配器-发射导轨之间的相互作用和作用载荷一直是设计人员很关注的数据,一般通过大量简化,进行简单计算,只能给出导弹和适配器相互作用载荷的数量级。近年来,仿真技术在各行业得到了广泛应用,但有关垂直发射仿真计算的文献却很少,从公开发表的文献来看,一般多采用多刚体动力学方法和刚柔相结合方法[9]进行垂直发射过程仿真分析。由于垂直发射结构复杂,结构动力学方法一般只能进行系统级模态分析[10],对发射过程中的弹箱相互作用很难进行仿真分析。针对以上问题,本文结合适配器中海绵层的试验数据,利用有限元软件 Abaqus 建立含有适配器的垂直发射系统非线性结构动力学模型,并对垂直发射过程进行仿真计算。
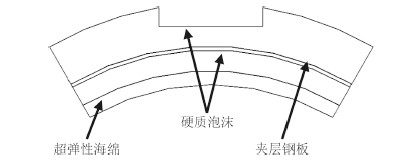
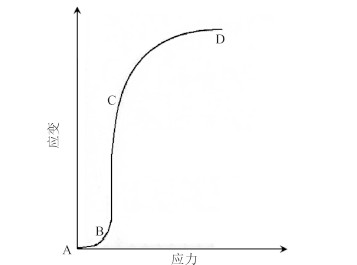
1 超弹性海绵材料本构模型某导弹的适配器由硬质泡沫、钢和超弹性海绵3种材料构成,结构如图 1所示。适配器预压缩量为3 mm,在适配器内侧与导弹接触面上采用过盈装配。适配器中硬质泡沫和钢均是线弹性材料,而超弹性海绵是一种多空腔、质轻、高度非线性材料,其受压应力-应变特征曲线如图 2所示。
|
图 1 适配器结构 Fig. 1 Schematic diagram of adapter |
|
图 2 海绵层应力-应变示意图 Fig. 2 Schematic diagram of stress and strain |
AB 段(弹性过程):应变小于5%,主要由海绵材料的空腔壁弯曲引起;
BC 段(屈曲过程):空腔壁弯曲达到极限时,开始发生屈曲,应力增加一点,而应变增加很多;
CD 段(密实化过程):由于空腔壁屈曲后变得密实,空腔消失,此时海绵材料所受的压缩主要是海绵材料分子之间的挤压。
超弹性海绵材料的变形特性类似于橡胶材料[11, 12]。橡胶是一种体应变不可压材料,而超弹性海绵材料为体应变可压。这类材料的变形能函数 W 是有势函数,以 Green-Lagrange 应变的主应变张量为变量。由于超弹性海绵为体应变可压,因此应变势能函数采用修正的Ogden-Hill应变能函数[13]:
| $ W = \sum\limits_{i = 1}^N {\frac{{2{\mu _i}}}{{\alpha _i^2}}[\lambda _1^{{\alpha _i}} + \lambda _2^{{\alpha _i}} + \lambda _3^{{\alpha _i}} - 3 + \frac{1}{{{\beta _i}}}({J^{ - {\alpha _i}{\beta _i}}} - 1)]} $ | (1) |
αi,μi,βi参数反映了材料的力学特性,需要根据单向试验数据或双向试验数据对应力采用非线性最小二乘法计算。由于这种材料在适配器中只承受径向压缩,因此单向试验数据足够反映该材料的径向力学特性。应变能函数W对于单向压缩试验的伸长率即为工程应变,根据式(1)可得工程应力-应变的关系:
| $ {T_U} = \frac{{\partial W}}{{\partial {\lambda _U}}} = \frac{2}{{{\lambda _U}}}\sum\limits_{i = 1}^N {\frac{{{\mu _i}}}{{{\alpha _i}}}\left( {\lambda _U^{{\alpha _i}} - {J^{ - {\alpha _i}{\beta _i}}}} \right)} ,\;1 \le N \le 6。 $ | (2) |
式(1)和式(2)中αi,μi,βi(1≤N≤6)的取值,应根据试验数据TUi 和 λUi(i = 1,2,…,M),采用最小二乘法计算。对于不同的海绵材料,N取值也不同,本文后续计算采用N=6。
2 舰载导弹垂直发射过程建模 2.1 有限元建模由于垂直发射系统结构比较复杂,建立有限元模型时必须做适当的简化处理,保留对系统动态特性影响较大的结构,忽略一些小的次要结构。简化后的有限元几何模型如图 6所示,有上下2道适配器(靠近发射箱口的为第1道适配器,靠近导弹尾部的为第2道适配器),每道适配器有左右2块,共计4块。由于装入发射箱后的适配器弹簧销压缩力相对适配器压缩力很小,因此本文不考虑弹簧销,但是要保证适配器理论接触面积、理论圆周长度和重量不变。理论接触面积是指适配器内表面与导弹的接触面积,理论圆周长度指适配器与导弹在圆周方向的接触长度。适配器通过外侧凹面与凸型长导轨接触。凸型长导轨有左右2根,2根凸型导轨通过垫板用螺栓与发射箱框架连接。由于导弹弹体刚度远大于适配器刚度,并且导弹外壁受适配器挤压后变形很小,所以把导弹建成刚体模型,在其质心上输入相应的质量和转动惯量。
|
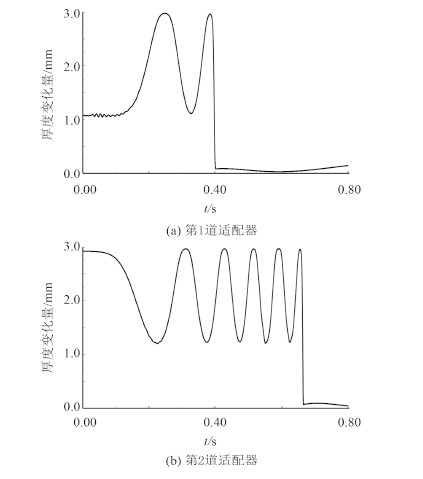
图 6 单块适配器厚度变化曲线 Fig. 6 Thickness change of the adapter |
有限元模型中适配器和滑动导轨均采用八节点六面体缩减积分单元,单块适配器单元数量为9 840个,单根导轨单元数量为13 970个,整个模型共有单元87 693个,节点110 250个;适配器与导轨和适配器与导弹之间均采用惩罚接触方法来模拟它们之间的相互作用关系。本文没有考虑弹簧销,为防止发射过程中适配器所受摩擦力太大而沿着导弹相对运动,适配器与导弹之间的摩擦系数取值要大于适配器与导轨的摩擦系数,本文取为0.3,适配器与导轨的摩擦系数取为0.1。
2.2 边界条件与载荷每根发射导轨采用6组螺栓与发射箱连接,如图 3所示。发射箱安装在发射井中,因此可认为导轨与发射箱的螺栓组连接处为固定,约束相应部位节点的全部自由度。发射过程中导弹、适配器、导轨受到的燃气流冲击力非常复杂,但相比于适配器与导弹、适配器与导轨之间的挤压力很小,可忽略不计,只考虑导弹受到的发动机推力。发射过程中导弹发动机喷出的燃气流温度很高,考虑到发射过程时间短暂,整个发射过程不到0.8 s,因此本文不考虑温度对发射系统的影响。整个发射过程中各部件还受到重力的作用。

|
图 3 适配器装配位置示意图 Fig. 3 Position of launcher and adapter |
采用有限元法建立的导弹发射过程瞬态动力学方程为:
| $ M\left\{ {\ddot u} \right\} + C\left\{ {\dot u} \right\} + K\left\{ u \right\} = \left\{ P \right\} $ | (3) |
由于式(3)是一个含有材料非线性和接触非线性的方程,因此无法像线性方程那样直接解耦采用模态叠加法计算,只能采用直接积分法计算。直接积分法解式(3)有隐式方法和显式方法2种方法。隐式方法在时间域采用 Newmark 积分法,对于t时刻用 Newton-Raphson法进行平衡迭代求解方程中的变量,求解涉及到刚度矩阵求逆计算,由于导弹与适配器离开发射筒后会在某些方向存在刚体位移,因此刚度矩阵[K]的求逆计算可能无法进行,所以隐式方法不适合本文;而显式方法采用中心差分法对时间域进行积分计算,无需对刚度矩阵求逆,求解方程不受刚体位移的影响。基于以上考虑,本文采用显式积分方法求解动力学方程。式(3)中的质量矩阵M、阻尼矩阵C 和刚度矩阵 K 在时刻t + Δt 利用上一个时间增量步计算得到的{u},$\left\{ {\dot{u}} \right\}$,{ü}进行修正。
对于时刻 t,方程(3)可写成如下形式:
| $ {\left\{ {\ddot u} \right\}_t} = {M^{ - 1}}\left( {{P_t} - {I_t}} \right)。 $ | (4) |
式中It为抗力矩阵,是由阻尼和刚度产生的抗力。
| $ {I_t} = C{\left\{ {\dot u} \right\}_t} + K{\left\{ u \right\}_t}。 $ | (5) |
根据中心差分法可以得到 t + Δt 时刻的速度向量和位移向量:
| $ {\left\{ {\dot u} \right\}_{t + \Delta t}} = {\left\{ {\dot u} \right\}_t} + \frac{{\Delta t}}{2}\left( {{{\left\{ {\ddot u} \right\}}_t} + {{\left\{ {\ddot u} \right\}}_{t + \Delta t}}} \right), $ | (6) |
| $ {\left\{ u \right\}_{t + \Delta t}} = {\left\{ u \right\}_t} + {\left\{ {\dot u} \right\}_t} \cdot \Delta t + \frac{{\Delta {t^2}}}{2}{\left\{ {\ddot u} \right\}_t}, $ | (7) |
对于 t - Δt 时刻而言,由式(6)可得:
| $ {\left\{ u \right\}_{t - \Delta t}} = {\left\{ u \right\}_t} - {\left\{ {\dot u} \right\}_t} \cdot \Delta t + \frac{{\Delta {t^2}}}{2}{\left\{ {\ddot u} \right\}_t}。 $ | (8) |
对式(6)和式(7)进行计算,可得到 t 时刻的速度向量和加速度向量:
| $ {\left\{ {\dot u} \right\}_t} = \frac{{{{\left\{ u \right\}}_{t + \Delta t}} - {{\left\{ u \right\}}_{t - \Delta t}}}}{{2\Delta t}}, $ | (9) |
| $ {\left\{ {\ddot u} \right\}_t} = \frac{{{{\left\{ u \right\}}_{t + \Delta t}} - 2{{\left\{ u \right\}}_t} + {{\left\{ u \right\}}_{t - \Delta t}}}}{{\Delta {t^2}}}。 $ | (10) |
将式(8)和式(9)改写成前向差分时间积分格式,可以得到$t+\frac{\Delta t}{2}$时刻的速度向量和t + Δt 时刻的位移向量:
| $ {\left\{ {\dot u} \right\}_{t + \frac{{\Delta t}}{2}}} = {\left\{ {\dot u} \right\}_{t - \frac{{\Delta t}}{2}}} + \frac{{\left( {\Delta {t_{t + \Delta t}} + \Delta {t_t}} \right)}}{2}{\left\{ {\dot u} \right\}_t}, $ | (11) |
| $ {\left\{ u \right\}_{t + \Delta t}} = {\left\{ u \right\}_t} + \Delta {t_{t + \Delta t}}{\left\{ {\dot u} \right\}_{t + \frac{{\Delta t}}{2}}}。 $ | (12) |
根据式(4)、式(11)和式(12)可以逐步计算出每一时间步的位移、速度和加速度向量,并且都是通过显式时间积分所得,因此该算法称为显式时间积分算法。但显式时间积分算法条件稳定,计算时间增量步或者临界稳定增量步与单元网格大小、材料特性有关,一般步长很小[9]。
预压缩量直接影响适配器与导轨之间的接触压力,而适配器与滑动导轨之间的摩擦力与接触压力成正比,摩擦力的大小直接影响导弹垂直发射时的动力学特性,因此在开始求解式(3)之前,需要对模型进行静平衡,把静平衡中的计算结果,包括应力、应变、位移等场变量数据作为式(3)的初始条件。静平衡的主要目的是使适配器海绵层的预压缩量产生相应的内应力,起到适配器预压缩的作用,并对重力载荷进行平衡分配,最终使导弹在适配器预压缩量产生的压力作用下与适配器和导轨处于一个静力学平衡状态。
3 仿真结果分析由于文中垂直发射系统结构动力学模型的自由度数量比较大,在普通计算机上很难计算完成,所以选择在HP XW 8600小型工作站上进行,并采用多线程并行计算,使得计算速度加快,节省计算时间,缩短武器研制周期。从计算结果中得到了发射过程中导轨和适配器的应力云图、适配器摩擦力变化曲线和适配器厚度变化曲线,如图 4~图 6所示。

|
图 4 导弹发射过程应力云图 Fig. 4 Adapter stress distribution during missile launching process |

|
图 5 适配器与导轨摩擦力曲线 Fig. 5 Friction force between adapter and lead rail |
图 4为导弹发射时适配器与导轨的应力云图。由图 4可看出,导轨的应力值很小,最大应力约为73 MPa,远小于导轨的许用应力极限,在安全范围内。
从图 4可看出,适配器摩擦力曲线变为0时为适配器脱离导轨接触离开发射筒的时间,第一道适配器在0.5 s(以动力学计算开始时刻作为时间起始点,下文相同)离开发射筒,第2道适配器在0.79 s 离开发射筒。在图 5中适配器厚度变化为0时也可以得到两道适配器离开发射筒的时间。两道适配器与导轨之间的摩擦力变化范围为300~520 N,并且摩擦力曲线是起伏波动的,波动周期逐渐变小。摩擦力波动的主要原因是,当适配器沿着导轨滑动时,滑动凸导轨在适配器的压力作用下发生弯曲变形,造成适配器内应力减小,适配器对导轨的接触压力变小;当适配器运动到导轨等间隔长度中间时,导轨挠度最大,适配器内应力最小,与导轨的接触压力也最小,所以摩擦力最小;当适配器运动到发射箱与导轨连接位置时,由于此位置是模型约束位置,导轨挠度最小,适配器内应力最大,适配器与导轨的接触压力也最大,所以摩擦力达到最大值。摩擦力曲线波动周期变小是由于导轨与发射箱之间等间隔长度固定,而导弹的运动是一个加速过程,因此周期会变小。由图 6可知,适配器厚度变化量Δ的变化范围是1.112~2.965 mm,小于预压缩量3 mm,因此在发射时箱内运动期间适配器不会脱落,能够正常工作。
4 结 语本文选用合理的适配器超弹性海绵材料本够模型,建立了含有大位移、大变形、接触和材料高度非线性的某舰载导弹垂直发射过程的有限元模型;采用显示中心差分法进行瞬态动力学计算,得到了发射过程中适配器与导轨的摩擦力和适配器厚度的变化规律,通过对数据曲线的分析,揭示了摩擦力曲线和适配器厚度变化曲线的波动原因以及波动周期逐渐变小的原因。计算结果表明适配器厚度变化量最大值小于其预压缩量,因此发射过程中适配器在发射箱内运动期间不会脱落,适配器设计合理。
| [1] | 王亚锋, 孙富春, 张友安, 等. 一种舰载垂直发射导弹的分段传递对准方法[J]. 系统仿真学报, 2009, 21(2):335-339 |
| [2] | 尹永鑫, 杨明, 王子才. 并联式运载器的垂直发射建模与控制[J]. 北京航空航天大学学报, 2008, 34(4):369-372, 376. |
| [3] | 郑友胜, 王良明. 火箭弹垂直发射动力学建模与仿真[J]. 飞行力学, 2008, 26(2):60-63. |
| [4] | MOORHEAD S B. The latest in ship weapon launchers-the vertical launching system[J]. Naval Engineers Journal, 1981, 93(2):90-96. |
| [5] | YOSHIMOTO B. Vertical launching system (VLS) technical assistance expert system (VTAEXS)[C]//Proceedings of the 11th conference on artificial intelligence for applications. Los Angeles, CA:IEEE, 1995:170-176. |
| [6] | 常卫伟. 舰载导弹垂直发射系统综述[J]. 舰载武器, 2002(4):47-52. |
| [7] | 郑宏建, 张兴有, 马洪霞. 航空导弹垂直发射系统特点分析[J]. 战术导弹技术, 2002(1):18-22. |
| [8] | 徐悦, 张振鹏, 陈小庆. 舰载导弹垂直发射技术研究进展[J]. 导弹与航天运载技术, 2007(3):22-25. |
| [9] | 徐悦, 田爱梅, 张振鹏, 等. 导弹垂直发射系统柔性多体动力学建模与仿真[J]. 兵工学报, 2008, 29(9):1083-1087. |
| [10] | 朱卫兵, 郜冶. 舰载导弹垂直发射装置模态分析与实验[J]. 哈尔滨工程大学学报, 1998, 19(2):39-44. |
| [11] | 庄茁, 由小川, 廖剑晖, 等. 基于ABAQUS的有限元分析和应用[M]. 北京:清华大学出版社, 2009. |
| [12] | BONET J, WOOD R D. Nonlinear continuum mechanics for finite element analysis[M]. Cambridge:Cambridge University Press, 1977. |
 2016, Vol. 38
2016, Vol. 38
