2. 北京信息科技大学网络文化与数字传播北京市重点实验室, 北京 100101
2. Beijing Key Laboratory of Internet Culture and Digital Dissemination Research, Beijing Information Science and Technology University, Beijing 100101, China
在海洋工程中,很多构件为圆柱结构,如钻井平台、深海油气立管等。涡激振动可导致构件疲劳、损坏,影响构件寿命和设备安全。胡卫兵[1]、曹淑刚等[2]以 CFX 为平台对圆柱绕流涡激振动进行了流固耦合数值模拟,分别对固体结构控制点的位移、压强和圆柱体的位移响应功率谱、两向振幅等进行了分析。蒋仁杰[3]运用格子 Bolzmann 方法,研究了弹性支撑单圆柱体涡激振动的力学系统,对圆柱振幅、斯特罗哈尔数与折合速度的关系进行了研究,观察到了一种主要存在于亚临界雷诺数区域中的偏移振动形态。丁林等[4]从振动控制的角度研究了分隔板对圆柱涡激振动的影响,圆柱-分隔板结构的振动频率比单独的圆柱绕流时低,振动频率与固有频率比值保持在 0.4 附近。目前,海洋工程的圆柱绕流涡激振动研究大多针对固体、流固耦合、减振等进行,因此从流场角度研究涡激振动有重要的工程价值。李威[5]等验证了 SST k-ω 湍流模型对低质量比弹性支撑刚性圆柱体涡激振动问题的有效性。本文采用 SST k-ω 湍流模型[6]基础上的 DES 方法,以海洋工程中深海油气立管为应用背景模拟涡激振动,分析了第一层网格高度、网格数量、时间步长对立管涡激振动升力系数、阻力系数、斯特罗哈尔数的影响,与文献结果进行了比较,验证了数值计算模型的正确性,进一步丰富了海洋工程的理论研究。
以粘性不可压空气为流体介质,不考虑传热,N-S 方程如下:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0, $ | (1) |
| $ \frac{{\partial {u_i}}}{{\partial t}} + \frac{{\partial \left( {{u_i}{u_j}} \right)}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + \nu \frac{{{\partial ^2}{u_i}}}{{\partial {x_i}\partial {x_j}}}, $ | (2) |
| $ \begin{array}{*{20}{l}} {\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + {u_i}\frac{{\partial \left( {\rho k} \right)}}{{\partial {x_i}}} = \;{P_k} - \frac{{\rho {k^{3/2}}}}{{{l_{k - \omega }}}} + \frac{\partial }{{\partial {x_i}}}\left[ {\left[ {{\mu _l} + \frac{{{\mu _l}}}{{{\sigma _k}}}} \right]\frac{{\partial k}}{{\partial {x_i}}}} \right],} \end{array} $ | (3) |
| $ \begin{array}{*{20}{l}} {\frac{{\partial \left( {\rho \omega } \right)}}{{\partial t}} + {u_i}\frac{{\partial \left( {\rho \omega } \right)}}{{\partial {x_i}}} = {C_\omega }{P_\omega } - {\beta _\omega }\rho {\omega ^2} + \;\frac{\partial }{{\partial {x_i}}}\left[ {\left[ {{\mu _l} + \frac{{{\mu _l}}}{{{\sigma _k}}}} \right]\frac{{\partial k}}{{\partial {x_i}}}} \right] + \;2\rho \left( {1 - {F_1}} \right)\frac{1}{\omega }{\sigma _{{\omega ^2}}}\frac{{\partial k}}{{\partial {x_i}}}\frac{{\partial \omega }}{{\partial {x_i}}}.} \end{array} $ | (4) |
涡粘系数
| $ {\mu _l} = \min \left[{\frac{{\rho k}}{\omega },\frac{{{a_1}\rho k}}{{\Omega {F_2}}}} \right], $ | (5) |
| $ {l_{k - \omega }} = \frac{{{k^{1/2}}}}{{{\beta _k}\omega }}, $ | (6) |
DES 方法用长度尺度替代 k- SST 中长度尺度,从而使得计算区域在附面层使用 k- SST 模型,在主流分离区域使用大涡模拟模型。
| $ l = min\left[{{l_{k - \omega }},{C_{{\text{DES}}}}\Delta } \right], $ | (7) |
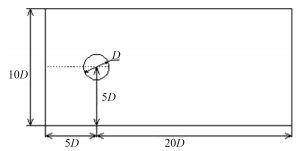
以圆的直径 D 为特征尺度,如图 1 所示,计算域为 10 D 25 D。图中计算域上游来流区域为 5 D,下游尾流区域为 20 D,圆柱距离上、下边界各为 5 D。文献[9]表明,该计算区域边界选取对流场的计算结果影响小。
|
图 1 计算域示意图 Fig. 1 Fluid computational domain |
运用 H-O 结构化网格离散计算域,靠近圆处加密网格,沿径向逐渐放大,如图 2 所示。

|
图 2 离散网格及放大图 Fig. 2 Mesh and its local magnification |
采用有限体积法(FVM)离散 Navier-Stokes 方程,压力速度耦合迭代采用 SIMPLE 算法,对流项采用二阶离散格式,扩散项采用二阶中心差分离散格式。对动量方程、标量输运方程采用了欠松弛技术。计算精度为 10-5。上下边界为滑移边界,圆边界为无滑移边界。流体从左至右流动,左侧设定为速度入口,右侧设定为压力出口,压力参考面为出口面。
3 结果及分析 3.1 网格第一层高度对结果影响文献[10]给出了 DES 方法在圆柱绕流模拟中的适合网格尺度。随着 CPU 运算能力的提升,可对网格尺度做更为精细的研究。文献[11]按经验公式
| $ {y^ + } = 0.172\frac{{\Delta y}}{D}{\text{ }}R{e^{0.9}}, $ | (8) |
估算 y+,并确定第一层网格控制点离壁面的距离。本文中,按式(8)估算得到的第一层网格高度称为Δy1。
NASA 粘性网格厚度计算器[12]也可估算网格第一层高度。NASA 粘性网格厚度计算器是基于空气介质在平板湍流中按照 Sutherland’s law[13] 来计算空气粘性厚度,估算Δy。本文中,按 NASA 粘性网格厚度计算器估算得到的第一层网格高度称为Δy2。计算得到Δy1 > Δy2。
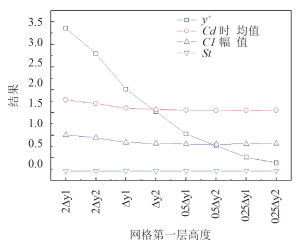
表 1 中网格数为 2.4 万,时间步长 0.002 s,不同网格第一层高度在 Re = 200 时的计算结果,由表可见,随着网格第一层高度Δy 的减小,降低,且前 4 组大于 1,在 0.5Δy1 之后,小于 1。前 4 组时均值、幅值随着Δy 的减小而降低,后 4 组时均值、幅值随着Δy 的减小没有明显降低,而是发生 2% 以内的小幅波动。前 4 组 St 为 0.212,后 4 组 St 为 0.216。
|
|
表 1 不同网格第 1 层高度 Re = 200 计算结果 Tab.1 Calculated results of different Δy when Re = 200 |
图 3 所示为表 2 中计算结果随Δy 的变化规律,由图可见,当Δy 减小到使得 y+ 小于 1 之后,继续减小对时均值、幅值、St 的影响小于 2%。可以看成 y 处漩涡的典型雷诺数,也反映粘性的影响随 y 的变化。DES 方法要求 = 1,0.51 得到的最接近 1,且小于 0.51 之后对计算结果影响小,因此本文之后的研究中以 0.51 来确定第 1 层网格高度。
|
图 3 Re = 200 计算结果随网格第一层高度变化规律 Fig. 3 Calculated results of different Δy when Re = 200 |
|
|
表 2 本文部分网格无关解结果与文献数据的比较 Tab.2 Comparison between calculated results of different meshes with the references |
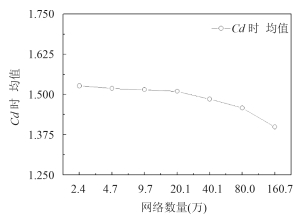
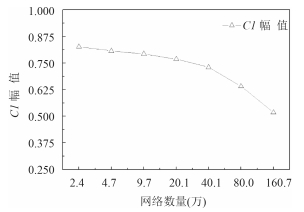
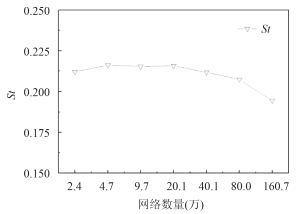
针对 Re = 200 的圆柱绕流流场,设置了网格数从 2.4 万逐渐增加至 160.7 万的 7 组网格,时间步长均为 0.001 s,计算结果随网格数的变化规律如图 4~6 所示。随着网格数量的增加,阻力系数时均值、升力系数幅值、斯特罗哈数均有下降的趋势。网格数为 2.4 万时,阻力系数时均值为 1.553、升力系数幅值为 0.808、斯特罗哈数为 0.216,网格数量增加至 160.7 万时,阻力系数时均值为 1.398、升力系数幅值为 0.517、斯特罗哈数为 0.194。表 2 为本文部分网格无关解结果与文献数据的比较,由表可知,增加网格数量使得计算结果更接近文献中实验结果。80.0 万网格幅值与文献[14]相差为 8.4%,St 相差为 8.9%,。160.7 万网格幅值与文献[14]相差为 26.1%,St 相差为 2.1%。涡激振动中最主要的性能参数为升力系数和斯特罗哈尔数,综合考虑 2 个参数的结果,80.0 万网格与实验结果更接近。与实验结果相差的可能原因在于计算模型是二维刚体,实验中为三维气动弹性模型。因此,下文将使用 80.0 万网格数量进行研究。
|
图 4 阻力系数时均值随网格数变化规律 Fig. 4 Drag coefficient of different meshes |
|
图 5 升力系数幅值随网格数变化规律 Fig. 5 lift coefficient of different meshes |
|
图 6 斯特罗哈尔数随网格数变化规律 Fig. 6 Strouhal number of different meshes |
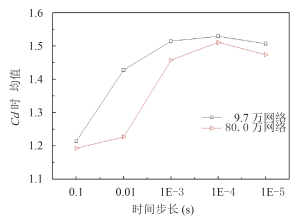
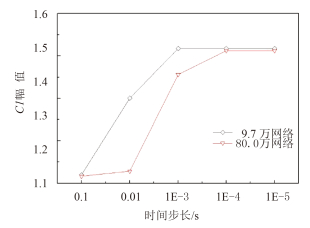
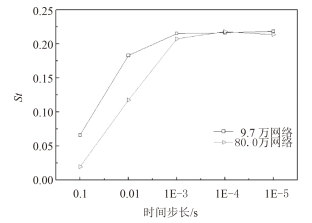
针对网格数量为 9.7 万和 80.0 万的 2 个网格,分别采取 0.1 s 到 1E-5 s 五组时间步长对 Re = 200 圆柱绕流流场进行计算,得到的结果如表 3、图 7 ~ 图 9 所示,由图可见,2 组网格的阻力系数时均值、升力系数幅值、斯特罗哈尔数都随着时间步长的减小而先增大,并在 0.001 s 之后趋于稳定。可知 0.001 s 的时间步长在该网格数量时较为适用,继续降低时间步长对计算精度提升不大,下文将采用 0.001 s 的时间步长。
|
|
表 3 两组网格 Re = 200 不同时间步长计算结果 Tab.3 Calculated results of different time steps when Re = 200 |
|
图 7 阻力系数时均值随时间步长变化规律 Fig. 7 Drag coefficient of different time steps |
|
图 8 升力系数幅值随时间步长变化规律 Fig. 8 Lift coefficient of different time steps |
|
图 9 斯特罗哈尔数随时间步长变化规律 Fig. 9 Strouhal number of different time steps |
图 7 为阻力系数时均值随时间步长变化规律,由图可见,9.7 万网格的阻力系数时均值曲线位于 80.0 万网格之下,在相同时间步长时,80.0 万网格的阻力系数时均值小于 9.7 网格,更接近文献中实验结果,进一步验证了本文 3.2 节的结论。升力系数幅值、斯特罗哈尔数亦有相同的规律。
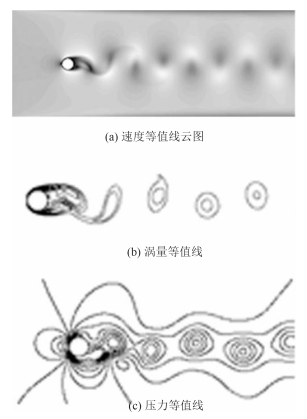
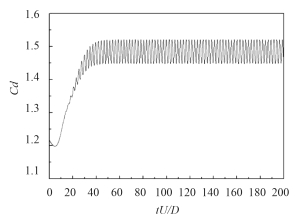
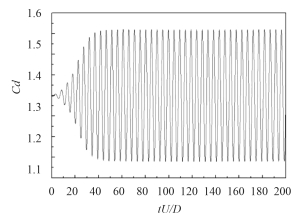
3.4 Re = 200 结果根据本文 3.1 ~ 3.3 节的研究,得到 Re = 200 时圆柱绕流涡激振动 DES 模拟结果,如表 4、图 10 ~ 图 12 所示。图 10中可见旋涡交替从圆柱两侧脱落,导致圆柱受到来自流场的阻力、升力均随时间周期性的脉动,升力脉动频率由旋涡脱落频率决定,由表 4 可见,斯特罗哈尔数为 0.207,旋涡脱落频率 f 为 6.06 Hz。由图 11和12 可见,升力脉动频率为阻力的一半,升力的时均值趋于 0。
|
|
表 4 Re = 200 计算结果 Tab.4 Calculated results when Re = 200 |
|
图 10 Re = 200 瞬时流场等值线云图 Fig. 10 Transient contours when Re = 200 |
|
图 11 Re = 200 阻力时程曲线 Fig. 11 Drag coefficient vs time when Re = 200 |
|
图 12 Re = 200 升力时程曲线 Fig. 12 Lift coefficient vs time when Re = 200 |
本文建立了圆柱绕流涡激振动的 CFD 计算模型,采用 H-O 分块结构化网格离散计算域,分析了 DES 方法的网格尺度和时间步长,对圆柱绕流涡激振动进行了数值模拟研究。本文研究范围内,可得到如下结论:
1)基于 SST k-ω 湍流模型的 DES 方法模拟低雷诺数圆柱绕流涡激振动结果合理;
2)随着网格第一层高度Δy 的减小,y+降低。按 0.5Δy1 确定 DES 方法的第一层网格高度可得到满足要求的;
3)增加网格数量可使计算结果更接近实验结果,但网格数量到一定程度后再增加对结果改善不明显。本文中 80.0 万网格结果最优;
4)减小时间步长可提高计算精度,需针对不同对象进行时间步长无关解研究。
| [1] |
胡伟. 高耸结构绕流与流固耦合的数值模拟[D]. 西安:西安建筑科技大学, 2010. HU Wei. Numerical simulation of wind pass high-rise structure and fluid-solid coupling[D]. Xi'an:Xi'an University of Architecture and Technology, 2010. |
| [2] |
曹淑刚, 黄维平, 顾恩凯. 考虑流固耦合的弹性圆柱体涡激振动研究[J]. 振动与冲击, 2015, 34(1):58-62. CAO Shu-gang, HUANG Wei-ping, GU En-kai. Study on vortex-induced vibration of an elastic cylinder considering fluid-structure interaction[J]. Journal of vibration and shock, 2015, 34(1):58-62. |
| [3] |
蒋仁杰. 圆柱绕流场涡致柱体振动的研究[D]. 杭州:浙江大学, 2013. JIANG Ren-jie. Research on vortex-induced vibrations in the flow around circular cylinders[D]. Hangzhou:Zhejiang University, 2013. |
| [4] |
丁林, 张力, 杨仲卿. 高雷诺数时分隔板对圆柱涡致振动的影响[J]. 机械工程学报, 2013, 49(14):133-139. DING Lin, ZHANG Li, YANG Zhong-qing. Effect of splitter plate on vortex-induced vibration of circular cylinder at high Reynolds number[J]. Journal of mechanical engineering, 2013, 49(14):133-139. |
| [5] |
李骏, 李威. 基于SST k-ω湍流模型的二维圆柱涡激振动数值仿真计算[J]. 舰船科学技术, 2015, 37(2):30-34. LI Jun, LI Wei. Numerical simulation of vortex-induced vibration of a two-dimensional circular cylinder based on the SST k-ω turbulent model[J]. Ship science and technology, 2015, 37(2):30-34. |
| [6] | STRELETS M. Detached eddy simulation of massively separated flows[R]. AIAA-01-0879. San Antonio, Texas:American Institute of Aeronautics & Astronautics, 2001. |
| [7] | MENTER R. Zonal Two equation k-turbulence models for aerodynamics flows[R]. AIAA-93-2906. Orlando, FL:American Institute of Aeronautics & Astronautics, 1993. |
| [8] |
顾春伟, 陈美兰, 李雪松, 等. DES模型在压气机叶栅中的应用研究[J]. 工程热物理学报, 2008, 29(12):2007-2010. GU Chun-wei, CHEN Mei-lan, LI Xue-song, et al. Application of DES model in the compressor cascade flow[J]. Journal of engineering thermophysics, 2008, 29(12):2007-2010. |
| [9] |
时忠民, 刘名名, 郭晓玲. 计算域对圆柱绕流数值模拟结果的影响[J]. 中国水运, 2013, 13(7):83-88. SHI Zhong-min, LIU Ming-ming, GUO Xiao-ling. Effect of flow field on flow around circular cylinder[J]. China water transport, 2013, 13(7):83-88. (未链接到本条文献英文信息) |
| [10] | SPALART P R. Young-person's guide to detached-eddy simulation grids[R]. NASA/CR-2001-211032. Washington:Boeing Commercial Airplanes, 2001 |
| [11] |
常书平, 王永生, 庞之洋. 用基于SST模型的DES方法数值模拟圆柱绕流[J]. 舰船科学技术, 2009, 31(2):30-33. CHANG Shu-ping, WANG Yong-sheng, PANG Zhi-yang. Numerical simulation of flow around circular cylinder using SST DES model[J]. Ship science and technology, 2009, 31(2):30-33. |
| [12] | NASA. Viscous grid spacing calculator[EB/OL]. 1997. http://geolab.larc.nasa.gov/APPS/YPlus/. |
| [13] | SUTHERLAND W. The viscosity of gases and molecular force[J]. Philosophical magazine, 1893, 36(223):507-531 |
| [14] | BRAZA M, CHASSAING P, MINH H H. Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder[J]. Journal of fluid mechanics, 1986, 165:79-130 |
| [15] |
魏志理, 孙德军, 尹协远. 圆柱尾迹流场中横向振荡翼型绕流的数值模拟[J]. 水动力学研究与进展(A辑), 2006, 21(3):299-308. WEI Zhi-li, SUN De-jun, YIN Xie-yuan. A numerical simulation of flow around a transversely oscillating hydrofoil in the wake of a circular cylinder[J]. Journal of Hydrodynamics, 2006, 21(3):299-308. |
 2016, Vol. 38
2016, Vol. 38
