随着减振降噪技术的发展,舰船辐射噪声越来越低,传统的单水听器测量方式难以满足低信噪比情况下目标辐射噪声量级评价的需求。采用声压水听器组成的常规基阵能够获得一定的空间增益,但要实现低频信号的测量,必须组成大尺度的阵型,对布放、后处理以及成本造成相当大的负担。矢量传感器可以同步、共点地获取声场的标量和矢量信息,丰富了信息处理的选择,同时它又具有尺寸小,抑制各向同性噪声干扰等优点[1, 2]。利用矢量传感器组成矢量阵可以提高测量增益,改善测试系统的性能。
以往的矢量阵波束形成方法都针对远场情况开展研究[3, 4, 5],而舰船辐射噪声测量通常要求在较近的距离进行,辐射源通常处于基阵的近场范围,且需要恒定束宽波束形成处理,以实现辐射噪声的无失真接收[6]。因此本文将从建立矢量阵近场信号模型入手,提出一种基于Kaiser窗的近场恒定束宽波束形成方法,并通过仿真验证上述算法的性能。
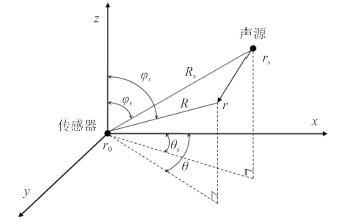
1 矢量阵近场波束形成基础 1.1 近场数学模型的建立建立如图 1 所示的坐标系。其中,声矢量传感器位于坐标原点,r0 = [0,θ,φ]T。Rs 表示声矢量传感器与位于坐标 rs =(Rs,θs,φs)处的入射声源的距离,则声矢量传感器的近场阵列流形向量可表示为[7]:
|
图 1 矢量传感器信号模型 Fig. 1 Signal model of single vector hydrophone |
| $ {a_{near}} = \left[{\begin{array}{*{20}{c}} {\cos {\theta _s}\sin {\phi _s}} \ {\sin {\theta _s}\sin {\phi _s}} \ {\cos {\phi _s}} \ {\frac{{ - {\rho _0}c}}{{\sqrt {1 + {{\left( {\frac{\lambda }{{2\pi {R_s}}}} \right)}^2}} }}{e^{j{\text{arctan}}\frac{\lambda }{{2\pi {R_s}}}}}} \end{array}} \right] $ | (1) |
从式(1)可看出,振速传感器的三维测量值与声压传感器测量值之间存在复相位差。该偏差由声源与传感器间的距离进行波长归一化后的 Rs/λ 和传播介质的 ρ0c 决定,与方位角和俯仰角无关。
当 Rs/λ→∞,近场阵列流形将收敛为如下形式:
| $ {a_{{\text{far}}}} = \left[{\begin{array}{*{20}{c}} {\cos {\theta _s}\sin {\phi _s}} \ {\sin {\theta _s}\sin {\phi _s}} \ {\cos {\phi _s}} \ { - {\rho _0}c} \end{array}} \right] $ | (2) |
由于矢量阵有四路输出,与阵元数目相同的声压阵相比,矢量阵可获得 4 倍数目的输出信号,因此,能够有更大的组合自由度,典型的波束形成方法概括如下[8]:
1)基于单矢量传感器输出信号处理的波束形成
将单矢量传感器看作一个子阵,每个子阵由 4 个传感器组成,对每个子阵输出的 4 个分量进行各种组合,再对输出量做加权延时或者其他处理方式形成波束。
①子阵各个分量相加再加权延时求和:
| $ \begin{gathered} B\left( {{f_c},{\theta _s},{\phi _s},{R_s}} \right) = \hfill \ {\left| {\sum\limits_{n = 1}^N {{w_n}} \left( {p + u + v + w} \right)a{{\left( {{f_c},{\theta _s},{\phi _s},{R_s}} \right)}^{\text{T}}}} \right|^2} \hfill \ \end{gathered} $ | (3) |
②子阵各个分量相乘再加权延时求和:
| $ \begin{gathered} B\left( {{f_c},{\theta _s},{\phi _s},{R_s}} \right) = \hfill \ {\left| {\sum\limits_{n = 1}^N {{w_n}} \left( {p{v_x}{v_y}{v_z}} \right)a{{\left( {{f_c},{\theta _s},{\phi _s},{R_s}} \right)}^{\text{T}}}} \right|^2} \hfill \ \end{gathered} $ | (4) |
这类波束形成的优点是可以充分利用矢量传感器对于白噪声的抑制能力 ,但其缺点是最终的波束输出只有与阵元数相同的自由度。
2)基于矢量传感器同类输出分量信号处理的波束形成
将每个矢量传感器输出分量中相同的分量加权延时求和进行波束形成,然后再对各个分量的波束形成结果做进一步处理,如相乘或者相加等。
①相加性子阵波束形成器的波束图为:
| $ \begin{array}{*{20}{l}} {B\left( {{f_c},{\theta _s},{\phi _s},{R_s}} \right) = } \ {\left| {\sum\nolimits_{n = 1}^N {\left( {{w_{np}}p + {w_{n{v_x}}}u + {w_{n{v_y}}}v + {w_{n{v_z}}}w} \right)} } \right. \times } \ {{{\left. {\left. {a{{\left( {{f_c},{\theta _s},{\phi _s},{R_s}} \right)}^{\text{T}}}} \right\}} \right|}^2}} \end{array} $ | (5) |
这里 ${w_{np}},{w_{n{v_x}}},{w_{n{v_y}}},{w_{n{v_z}}} $ 分别是 4 个子阵第 n 个阵元的加权量。
②相乘性子阵波束形成器的波束图为:
| $ \begin{array}{*{20}{l}} {B\left( {{f_c},{\theta _s},{\phi _s},{R_s}} \right) = } \ {\quad \left| {\left\{ {\sum\nolimits_{{\text{n = 1}}}^{\text{N}} {{w_{np}}} pa{{\left( {{f_c},{\theta _s},{\phi _s},{R_s}} \right)}^{\text{T}}}} \right\} \times } \right.} \ {\quad {{\left. {\left\{ {\sum\nolimits_{{\text{n = 1}}}^{\text{N}} {{w_{n{v_y}}}{v_y}a{{\left( {{f_c},{\theta _s},{\phi _s},{R_s}} \right)}^{\text{T}}}} } \right\}} \right|}^2}} \end{array} $ | (6) |
这类子阵的优越性在于充分利用了矢量传感器丰富的输出信号,一个 N 元的矢量阵最大将具有 4N-1 个波束形成冗余度。
另外,也可以将两类方法进行组合,将这种组合波束形成称之为矢量阵混合波束形成,典型的组合方式如下(为简化说明,这里忽略加权项):
| $ B = {\left| { \sum\nolimits_{n = 1}^N \left( {{p_i}{v_{{x_i}}}} \right) \sum\nolimits_{n = 1}^N {p_i}} \right|^2} $ | (7) |
| $ B = {\left| {\sum\nolimits_{n = 1}^N {\left( {{p_i}\left( {{v_{{x_i}}} + {v_{{y_i}}} + {v_{{z_i}}}} \right)} \right)} \sum\nolimits_{n = 1}^N {{p_i}} } \right|^2} $ | (8) |
| $ B = {\left| {\sum\nolimits_{n = 1}^N \left( {{p_i} + {v_{{y_i}}}} \right)\sum\nolimits_{n = 1}^N {v_{{y_i}}}} \right|^2} $ | (9) |
恒定束宽波束形成器的设计通常采用以下 2 种思路[9]:1)随着频率的变化来改变基阵的基元数目或者基阵等效孔径;2)随着频率的变化而改变各阵元的加权向量。本文主要采用后者开展研究工作。
首先将宽带信号分成 N 个子带,然后求出与每个子带中心频率 fi(i = 1,2,···,N)相对应的近场矢量阵波束图 p(fi,θs,Rs),这里仅考虑二维平面情况(φs = 90°)。由于各子带之间频率存在较大变化,造成不同频率对应的主波束宽度不一致。需要寻找一个约束条件,使其能够对于权系数作出约束,达到恒定束宽的目的。
设在频率 fi 下的权矢量为 W(fi,θs,Rs),则近场情况下阵列的波束图 P(fi,θs,Rs)与参考波束图 P0(fi,θs,Rs)之间的差异可用误差来度量[10]:
| $ e\left( {{f_i},{R_s}} \right) = \int_{{\theta _1}}^{{\theta _2}} {\left| {P\left( {{f_i},{\theta _s},{R_s}} \right) - {P_0}\left( {{f_0},{\theta _s},{R_s}} \right)} \right|{\text{d}}{\theta _s}} $ | (10) |
| $ P\left( {{f}_{i}},{{\theta }_{s}},{{R}_{s}} \right)={{W}^{\text{T}}}\left( {{f}_{i}},{{\theta }_{s}},{{R}_{s}} \right)p\left( {{f}_{i}},{{\theta }_{s}},{{R}_{s}} \right) $ | (11) |
式(11)为基阵对频率为 fi、方向角 θs 和距离 Rs 处单位功率球面波的响应函数。[θ1,θ2] 是波束扫描覆盖范围,则其均方误差为:
| $ MSE = \xi \left( {{f_i}} \right) = E\left\{ {e{{\left( {{f_i}} \right)}^2}} \right\} $ | (12) |
为使主波束在频率变化范围内保持恒定,要求在该频率下使得 ξ(fi) 取得最小,即
| $ \mathop {\min }\limits_{w\left( {{f_n}} \right) \ne 0} \xi \left( {{f_n}} \right),{f_n} \in \left[{{f_l},{f_h}} \right],n = 1,2,\cdots ,K $ | (13) |
若满足上述条件,在频率 fi 处由式(13)求解得到
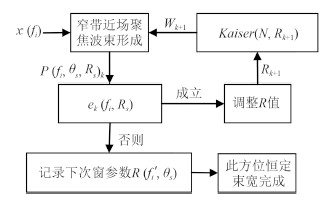
为达到抑制旁瓣,控制零点等目的,一般用加权来进行束控。这里给出一种利用 Kaiser 窗来求解权系数的方法,设计流程如图 2 所示。根据恒定束宽设计精度需求,确定误差 e(fi,Rs)门限 ξ。如果 e(fi,Rs)> ξ,则对于每一频率fi通过不断调整窗参数值,改变基阵加权矢量W,从而调整主聚焦波束图 P(fi,θs,Rs)与参考波束图 P0(fi,θs,Rs)逐步趋近于相同,满足收敛要求。
|
图 2 计算加权量的流程图 Fig. 2 Flow chart for calculating the weighting vector |
图 2 中包含一个反馈结构,反映出求解 W 过程为自适应迭代过程。图中的 x(fi)为信号的输入矢量,下标 k 表示第 k 次迭代的结果,ek(fi,Rs)为经过 k 次迭代后处理频率与参考频率的近场聚焦波束主瓣内的误差。在迭代过程中,只有对 R 值调整合理,ek(fi,Rs)才将逐渐变小,最后趋近于门限 ξ。
在进行恒定束宽波束形成器设计过程中,通常选取基阵的最低工作频率为参考频率,并从低频子带向高频子带逐步进行恒定束宽处理。由于频率越高主瓣越窄,信号频率 fi' 的恒定束宽处理完成后,记下各个方位的 Kaiser 窗参数 R(fi',θs),那么进行信号更高频率 fi 的恒定束宽处理时,就可以将上次恒定束宽 Kaiser 窗参数作为初始值,再结合优化选择窗函数参数,确定频率 fi 的第 k + 1 次窗函数参数${R_{k + 1}} = R({f_i}',{\theta _S}) + \sum _{i = 1}^{{\text{ }}k + 1}{\rho ^{N - i}}$,达到既提高恒定束宽精度又减少计算量的效果。
Kaiser 窗有长度参数 N 和形状参数 β 2 个参数。在利用 Kaiser 窗进行恒定束宽设计时,多数选择均匀变化参数的窗函数,研究发现参数均匀变化的窗函数有很多弊端,当参数较小时,较小的参数变化就可引起窗函数值发生较大的变化。如果在恒定束宽处理中应用参数均匀变化的窗函数,必然会导致在较小窗参数下,处理频率相邻循环的波束主瓣变化大,从而引起恒定束宽处理精度差,甚至会超出参考波束要求的误差范围,导致恒定束宽波束形成失败。因此,本文采用窗函数参数变化的步长随指数变化,如下式:
| $ \beta = \sum {{\text{ }}^{(N - k)}} $ | (14) |
式中: β 为窗函数参数变化的步长,ρ一般取 0.9 ~ 1 之间的数,这里取 0.995;N 为一个较大的整数,限定了参数最大取值范围;k 为循环次数,是 1 ~ N 之间的整数。窗函数参数随指数变化时,参数变化率在所有参数处都较小,必然会导致在所有窗参数下,处理频率的相邻循环波束主瓣变化较小,从而提高恒定束宽处理精度,避免恒定束宽波束形成失败。
综上所述,矢量阵近场恒定束宽波束形成器的设计过程如下:
1)根据接收信号的工作频率,将矢量阵的工作频段划分为若干个子带,确保每个子带满足窄带条件;
2)选择合适的矢量阵声压和振速组合形式,在每个子带内分别进行波束形成;
3)确定信号参考频率,为使恒定束宽后的波束不出现栅瓣,选取信号最低子带频率为参考频率,将该频率处的波束图当作参考波束图,利用提出的恒定束宽方法分别对各个子带进行恒定束宽处理,得到各个子带的加权系数,并对各个子带进行加权修正;
4)将修正后的权系数对矢量阵输入信号进行加权处理,就可以得到宽带波束输出,实现宽带信号的不失真接收。
3 设计实例针对本文提出的矢量阵近场恒定束宽波束形成方法,下面通过具体的设计实例来验证算法的性能。仿真过程中,选取矢量阵的阵元数为 17,阵元均匀分布于 x 轴的正负半轴,阵元间距为 0.75 m。这里,定义扫描区域横坐标为 x:(- 90 m ~ 90 m),纵坐标为 y:(- 60 m ~ 60 m),设定聚焦步长为 2 m,聚焦平面距矢量阵的垂距为 30 m,预设声源位置为(0,15,0)。
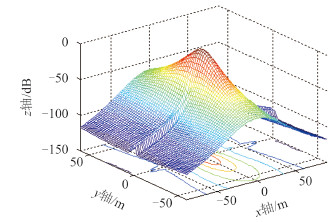
采用式(9)所示的波束表达式设计近场聚焦波束,波束聚焦结果如图 3 所示。图中:x = Rs∙sinθs,y = Rs∙cosθs。从图中可看出,采用矢量阵近场聚焦处理可以准确获取声源的空间位置。
|
图 3 900 Hz 频率处的三维聚焦波束 Fig. 3 3D focused beampattern of 900Hz frequency |
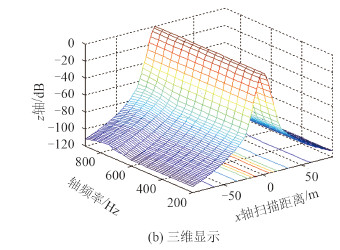
假设矢量阵的工作频带为 200 ~ 900 Hz,以 200 Hz 为参考频率,将工作频带均匀划分为 15 个子带,设计恒定束宽波束形成器。设计结果如图 4 所示。从图 4 可以看出,所有频率主旁瓣一致性都很好,满足恒定束宽设计要求。
|
图 4 近场恒定束宽波束图 Fig. 4 Near-field beampattern of CBB |
本文从舰船辐射噪声测量角度出发,以矢量阵为研究对象,建立了矢量阵近场信号模型,讨论基于单矢量传感器输出量处理和基于阵列同类输出分量相乘处理的波束形成方法。针对恒定束宽波束形成问题,利用 Kaiser 窗的特点,给出了一种基于 Kaiser 窗的近场恒定束宽波束形成方法,通过设定窗函数参数变化的步长随指数变化,使设计的波束响应逐渐趋近于理想的波束响应,提高了恒定束宽波束形成器的设计精度,并通过仿真试验验证了上述算法的性能。
| [1] | TICHAVSKY P, WONG K T, ZOLTOWSKI M D. Near-field/far-field azimuth and elevation angle estimation using a single vector hydrophone[J]. IEEE Transactions on Signal Processing, 2001, 49(11):2498-2510. |
| [2] | WU Y I, WONG K T. Acoustic near-field source-localization by two passive anchor-nodes[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1):159-169. |
| [3] | HAWKES M, NEHORAI A. Acoustic vector-sensor beamforming and Capon direction estimation[J]. IEEE Transactions on Signal Processing, 1998, 46(9):2291-2304. |
| [4] | HAWKES M, NEHORAI A. Wideband source localization using a distributed acoustic vector-sensor array[J]. IEEE Transactions on Signal Processing, 2003, 51(6):1479-1491. |
| [5] | JAUTAIKIS E P. Linear and adaptive plane wave beamforming with towed array of acoustic vector sensors[D]. NPS Thesis, M.S. Engineering Acoustics, 2007. |
| [6] | 王之程, 陈宗岐, 于沨, 等. 舰船噪声测量与分析[M]. 北京:国防工业出版社, 2004. |
| [7] | WU Y I, WONG, K T, LAU S K. The acoustic vector-sensor's near-field array-manifold[J]. IEEE Transactions on Signal Processing, 2010, 58(7):3946-3951. |
| [8] | SMITH K B, VAN LEIJEN A V. Steering vector sensor array elements with linear cardioids and nonlinear hippioids[J]. The Journal of the Acoustical Society of America, 2007, 122(1):370-377. |
| [9] | WU Y I, Wong, K T. A directionally tunable but frequency-invariant beamformer on an acoustic velocity-sensor triad to enhance speech perception[J]. The Journal of the Acoustical Society of America, 2012131(51):3891-3902. |
| [10] | 王之海, 王大成, 曾武. 利用Chebyshev窗函数获得恒定束宽加权矩阵的数值算法[J]. 海洋技术, 2009, 28(3):50-53. |
 2016, Vol. 38
2016, Vol. 38
