为克服单站纯方位目标运动分析(TMA)的可观测性,观测站平台需要进行有目的的机动,考虑到观测站在机动过程中易于暴露自己,甚至丢失目标,因此保持已有运动方向不变,寻找解决系统的可观测性方法,进而估计目标要素,一直是研究者探索的问题。增加独立于方位的频率信息是一种解决问题的思路,此时不需要观测站机动[1]。本文只研究单观测站情形下的目标要素解算问题。在如何利用方位和频率信息进行目标运动要素估计方面,已有成果[2, 3]主要是利用 TMA 的伪线性估计器作为初始解,然后结合方位和频率的非线性观测模型,利用非线性最优化算法对匀速直线运动目标进行无源定位。文献[2, 3]做法的共同点是将方位和频率的残差统一处理,利用非线性最优化算法进行目标要素估计,这种做法增加了目标状态变量的维数,计算量大,不利于工程的实现,此外目标状态变量维数的增加,加重了算法中矩阵的复共线性,矩阵的可逆性减弱,计算结果易受到舍入误差的影响。文献[4, 5]将观测方程转化为伪线性方程,利用最小二乘法把方位、线谱频移信息融合在一个滤波器中滤波,进行目标运动分析。但是目标状态变量的处理方法与上述相同,带来的问题是状态转移矩阵和测量矩阵为多维,矩阵的可逆性减弱。不同于上述文献做法,文献[6]将方位和频率2个观测量,分别建立滤波器,然后利用融合的方法,建立了新的 TMA 方法,这种独立处理信息的方法由于每一个系统的状态变量维数减少,系统可观测性增强,利于目标要素估计的收敛,但文献[6]在频率滤波器中利用了近似处理方法,在实际中,当线谱频率较大时,会带来较大误差。
利用文献[6]思想,不同于其算法,基于目标和观测站均作匀速直线运动时,可以估计相对速度与距离比的事实[7, 8],以及多普勒频移可以估计目标相对速度(没有近似处理)的事实,建立一种新的滤波算法,讨论不同情形下滤波算法的性能,并通过海试数据验证方法的可行性。
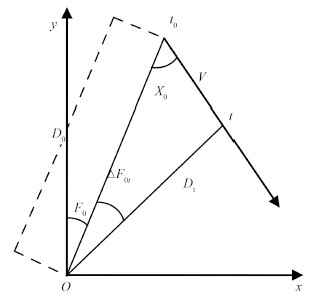
以下研究的问题总假设目标和观测站作匀速直线运动,利用单观测站获得的方位和多普勒频移信息,估计目标要素。两者的基本相对态势如图 1所示。
|
图 1 观测站和目标相对态势 Fig. 1 Relative scenario of observer and target |
设 fs 为目标的辐射频率,frt 为 t 时刻的接受频率,c 为声速,Vw和Vm 分别为观测器和目标的速度,V 为目标相对速度,Cw和Cm分别为观测器和目标的航向,$\Delta {{F}_{0t}}\overset{\Delta }{\mathop{=}}\,{{F}_{t}}-{{F}_{0}}$ 为 t 时刻与 t0 时刻的方位差,X0和Xt 分别为初始时刻 t0及t 时刻的目标舷角,D0为目标初始距离。结合图 1,有接收频率
| $ {f_{rt}} = {f_s}\left( {1 + \frac{V}{c}\cos {X_t}} \right) $ | (1) |
注意到${X_t} = {X_0} + \Delta {F_{0t}}$,式(1)转化为
| $ {f_{rt}} \! = \!{f_s}\left( {1 \!+ \!\frac{{V\cos {X_0}}}{c}\cos \Delta {F_{0t}} - \frac{{V\sin {X_0}}}{c}\sin \Delta {F_{0t}}} \right) $ | (2) |
式中:θ1 = V cos X0,θ2 = V sin X0,fri,i = 0,1,$\cdots $,n 为t0,t1,$\cdots $,tn 时刻的接受频率,则由式(2)知
| $ \begin{align} & {{f}_{ri}}={{f}_{s}}\left( 1+\frac{\cos \Delta {{F}_{0i}}}{c}{{\theta }_{1}}-\frac{\sin \Delta {{F}_{0i}}}{c}{{\theta }_{2}} \right)\text{,} \ & i=0\text{,}1\text{,}2\text{,}\cdots n \ \end{align} $ | (3) |
进一步有
| $ \frac{{{f}_{ri}}}{{{f}_{r0}}}=\frac{1+\frac{\cos \Delta {{F}_{0i}}}{c}{{\theta }_{1}}-\frac{\sin \Delta {{F}_{0i}}}{c}{{\theta }_{2}}}{1+\frac{1}{c}{{\theta }_{1}}}\text{,}i=1\text{,}2\text{,}\cdots \text{,}n $ | (4) |
式中${y_{i0}} = \displaystyle\frac{{{f_{ri}}}}{{{f_{r0}}}}$,整理式(4)得
| $ \begin{align} & {{y}_{i0}}-1=\frac{\cos \Delta {{F}_{0i}}-{{y}_{i0}}}{c}{{\theta }_{1}}-\frac{\sin \Delta {{F}_{0i}}}{c}{{\theta }_{2}}\text{,} \ & i=1\text{,}2\text{,}\cdots \text{,}n \ \end{align} $ | (5) |
利用最小二乘法得到参数的估计满足方程组:
| $ {{A}^{\text{T}}}A\theta ={{A}^{\text{T}}}y $ | (6) |
其中:
$ \begin{array}{*{35}{l}} \begin{align} & A=\left( \begin{matrix} \frac{\cos \Delta {{F}_{01}}-{{y}_{10}}}{c} & -\frac{\sin \Delta {{F}_{01}}}{c} \\ [8pt]\frac{\cos \Delta {{F}_{02}}-{{y}_{20}}}{c} & -\frac{\sin \Delta {{F}_{02}}}{c} \\ [8pt]\cdots & \cdots \\ [8pt]\frac{\cos \Delta {{F}_{0n}}-{{y}_{n0}}}{c} & -\frac{\sin \Delta {{F}_{0n}}}{c} \\ \end{matrix} \right)\text{;} \\ & \theta =\left( \begin{matrix} {{\theta }_{1}} \\ {{\theta }_{2}} \\ \end{matrix} \right) \\ \end{align} \\ y=\left( \begin{matrix} {{y}_{10}}-1 \\ {{y}_{20}}-1 \\ \vdots \\ {{y}_{n0}}-1 \\ \end{matrix} \right) \\ \end{array} $
当系数矩阵为满秩矩阵时,参数的估计为
| $ \hat{\theta }={{\left( {{A}^{\text{T}}}A \right)}^{-1}}{{A}^{\text{T}}}y $ | (7) |
于是得到目标舷角满足:
| $ \tan {{X}_{0}}=\frac{{{\theta }_{2}}}{{{\theta }_{1}}} $ | (8) |
目标相对速度为:
| $ V = \sqrt {\theta _1^2 + \theta _2^2} $ | (9) |
利用相对运动规律,可得目标速度为
| $ {V_m} = \sqrt {{V^2} + V_w^2 - 2V{V_w}\cos ({X_0} + {C_w})} \text{,} $ | (10) |
目标航向满足:
| $ \sin \left( {{C_m} - {C_w}} \right) = \frac{V}{{{V_m}}}\sin \left( {{C_w} + {X_0}} \right) $ | (11) |
式(6)是否存在唯一解,只需要验证其中的 A 矩阵是列满秩矩阵即可,进一步只需要验证 A 矩阵前 2 行组合的子矩阵是 2 阶满秩矩阵即可。
结合式(4),因为
$ \begin{array}{*{35}{l}} \left( \cos \Delta {{F}_{01}}-{{y}_{10}} \right)\sin \Delta {{F}_{02}}-\left( \cos \Delta {{F}_{02}}-{{y}_{20}} \right)\sin \Delta {{F}_{01}}= \\ \left( \cos \Delta {{F}_{01}}-\frac{{{f}_{r1}}}{{{f}_{r0}}} \right)\sin \Delta {{F}_{02}}-\left( \cos \Delta {{F}_{02}}-\frac{{{f}_{r2}}}{{{f}_{r0}}} \right)\sin \Delta {{F}_{01}}= \\ \sin \left( \Delta {{F}_{02}}-\Delta {{F}_{01}} \right)+\frac{{{f}_{r2}}}{{{f}_{r0}}}\sin \Delta {{F}_{01}}-\frac{{{f}_{r1}}}{{{f}_{r0}}}\sin \Delta {{F}_{02}}= \\ \sin \left( \Delta {{F}_{02}}-\Delta {{F}_{01}} \right)+ \\ \frac{c\left( \sin \Delta {{F}_{01}}-\sin \Delta {{F}_{02}} \right)+V\cos {{X}_{0}}\sin \left( \Delta {{F}_{01}}-\Delta {{F}_{02}} \right)}{c+V\cos {{X}_{0}}}= \\ \frac{c\left[ \sin \left( \Delta {{F}_{02}}-\Delta {{F}_{01}} \right)+\sin \Delta {{F}_{01}}-\sin \Delta {{F}_{02}} \right]}{c+V\cos {{X}_{0}}}= \\ \frac{4c\sin \frac{\Delta {{F}_{02}}-\Delta {{F}_{01}}}{2}\sin \Delta {{F}_{02}}\sin \Delta {{F}_{01}}}{c+V\cos {{X}_{0}}} \\ \end{array} $
可见,当目标和观测器不是相向或相离运动时,A 矩阵是列满秩矩阵,此时式(6)存在唯一解,即系统可观测。
2 利用目标方位信息估计目标相对速度距离比利用上述记号,并设 Vx和Vy 分别为目标相对于观测站速度 V 的 x 轴和y 轴分量。当输入目标方位Fk 时,目标方位 Fk 与 D0,Vx,Vy 的关系或测量模型为[7, 8, 9]
| $ \frac{\sin {{F}_{k}}}{\cos {{F}_{k}}}=\text{tan}{{F}_{k}}=\frac{{{D}_{0}}\sin {{F}_{0}}+{{V}_{x}}({{t}_{k}}-{{t}_{0}})}{{{D}_{0}}\cos {{F}_{0}}+{{V}_{y}}({{t}_{k}}-{{t}_{0}})}\text{,} $ | (12) |
$ \Leftrightarrow \sin ({{F}_{k}}-{{F}_{0}})=({{t}_{k}}-{{t}_{0}})\cos {{F}_{k}}\cdot \frac{{{V}_{x}}}{{{D}_{0}}}-({{t}_{k}}-{{t}_{0}})\sin {{F}_{k}}\cdot \frac{{{V}_{y}}}{{{D}_{0}}} $
上述式(12)左边式子可看作为观测值,利用最小二乘法可得到相对参数 $\frac{{{V_x}}}{{{D_0}}}$和$\frac{{{V_y}}}{{{D_0}}}$ 的估计满足下列方程组:
| $ {{B}^{\text{T}}}B\Theta ={{B}^{\text{T}}}Y $ | (13) |
其中
$ {{B}^{\text{T}}}B=\left( \begin{matrix} \begin{align} & \sum\limits_{i=1}^{n}{{{\left( {{t}_{i}}-{{t}_{0}} \right)}^{2}}{{\cos }^{2}}{{F}_{i}}}-\sum\limits_{i=1}^{n}{{{\left( {{t}_{i}}-{{t}_{0}} \right)}^{2}}\cos {{F}_{i}}}\sin {{F}_{i}} \\ & -\sum\limits_{i=1}^{n}{{{\left( {{t}_{i}}-{{t}_{0}} \right)}^{2}}\cos {{F}_{i}}}\sin {{F}_{i}}\sum\limits_{i=1}^{n}{{{\left( {{t}_{i}}-{{t}_{0}} \right)}^{2}}{{\sin }^{2}}{{F}_{i}}} \\ \end{align} \\ \end{matrix} \right) $
$ \begin{gathered} \Theta = \left( {\begin{array}{*{20}{c}} {\frac{{{V_x}}}{{{D_0}}}\frac{{{V_y}}}{{{D_0}}}} \end{array}} \right){\text{,}} \hfill \\ {B^{\text{T}}}Y = \left( {\begin{array}{*{20}{c}} \begin{gathered} \sum\limits_{i = 1}^n {\left( {{t_i} - {t_0}} \right)\cos {F_i}\sin ({F_i} - {F_0})} - \hfill \\ \sum\limits_{i = 1}^n {\left( {{t_i} - {t_0}} \right)\sin {F_i}\sin ({F_i} - {F_0})} \hfill \\ \end{gathered} \end{array}} \right) \hfill \\ \end{gathered} $
可见,BTB 为满秩矩阵,系统可测,从而得到参数 Θ 的最小二乘估计为
| $ \hat{\Theta }={{\left( {{B}^{\text{T}}}B \right)}^{-1}}{{B}^{\text{T}}}Y $ | (14) |
式中$\displaystyle\frac{V}{{{D_0}}}$的估计为$\sqrt {\displaystyle\frac{{V_x^2}}{{D_0^2}} + \displaystyle\frac{{V_y^2}}{{D_0^2}}} $。
3 算法步骤结合上述两节的内容,基于目标方位和多普勒频移信息,估计目标要素的算法为:
1)利用式(14),估计第 n 时刻目标相对速度距离比;
2)利用式(7),估计第 n 时刻参数 θ1,θ2;
3)利用式(10)和式(11),估计目标速度和航向;
4)利用步骤 1 和步骤 3 得到的参数,估计和参数间的关系,估计目标初始距离。
4 仿真与试验数据验证仿真条件见表 1,其中初始距离选择了远距离和近距离2种情况。为验证方法的可行性和有效性,下面从仿真和试验2个方面对上述方法进行验证。
|
|
表 1 目标和观测器运动要素 Tab.1 The motion elements of target and observer |
仿真条件见表 1,其中初始距离选择远距离和近距离2种情况。
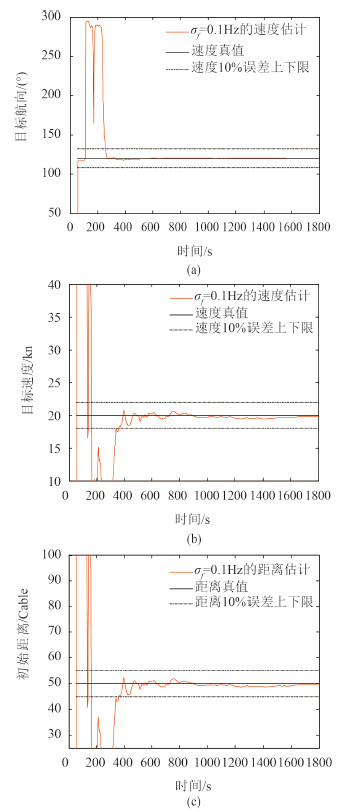
图 2 和图 3 分别给出了初始距离 50 链,方位误差为0,多普勒频移误差为 0.1 Hz和0.3 Hz条件下的仿真结果。结果显示,随着多普勒频移误差的增大,收敛时间增长,时间都在 10 min以内。
|
图 2 方位误差为0,多普勒频移误差为0.1 Hz的解算结果 Fig. 2 Results with zero error of bearing and 0.1 Hz error of Doppler frequency shift |
|
图 3 方位误差为0,多普勒频移误差为0.3 Hz的解算结果 Fig. 3 Results with zero error of bearing and 0.3 Hz error of Doppler frequency shift |
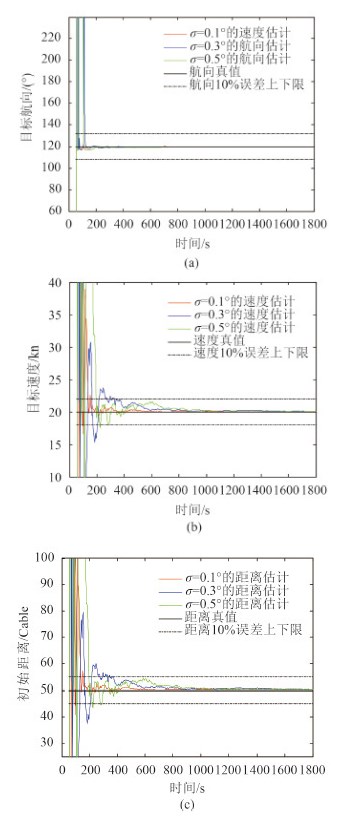
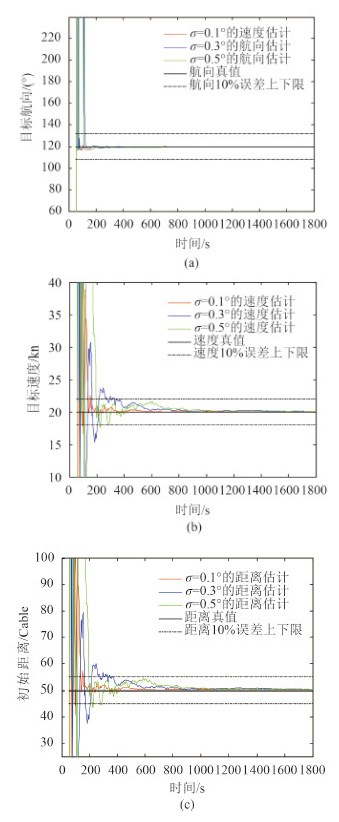
图 4 给出方位误差为 0.1°,0.3°,0.5°,多普勒频移误差为 0 Hz 条件下的仿真结果。结果显示,目标要素的估计收敛时间少于 10 min,方位误差的大小影响收敛时间。
|
图 4 方位误差为0.1°,0.3°,0.5°,多普勒频移误差为0 Hz的解算结果 Fig. 4 Results with 0.1°,0.3°,0.5° error of bearing and 0 Hz error of Doppler frequency shift |
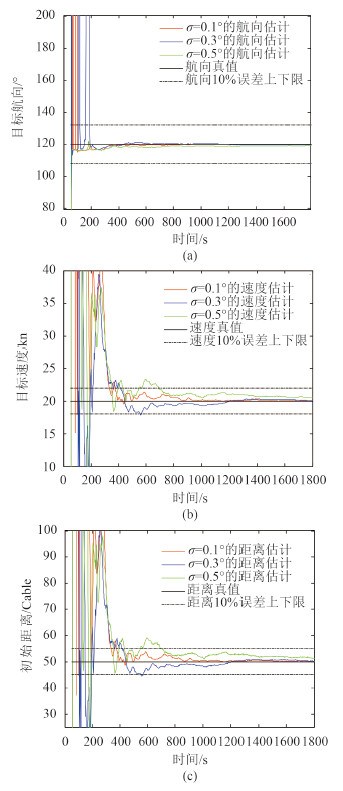
图 5 显示了当存在多普勒频移误差时,与图 4 相比,目标要素的估计收敛时间均增大,目标航向的收敛时间小于 10 min。进一步增大多普勒频移误差,收敛的时间进一步增大。由此看出,多普勒频移误差对目标要素的估计较为敏感。
|
图 5 不同距离下方位误差为0.1°,0.3°,0.5°,多普勒频移误差为0.1 Hz的解算结果 Fig. 5 Results with 0.1°,0.3°,0.5° error of bearing and 0.1 Hz error of Doppler frequency shif |
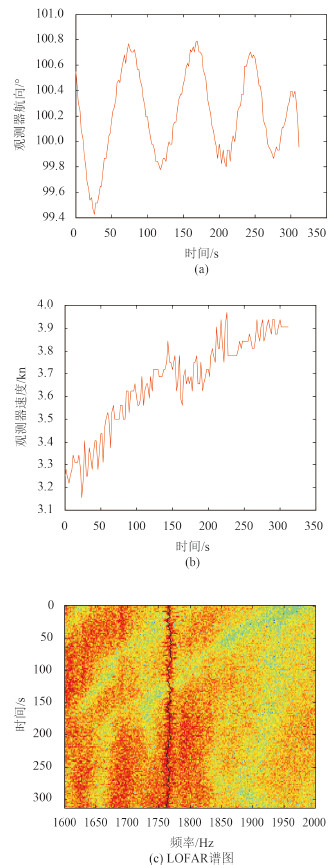
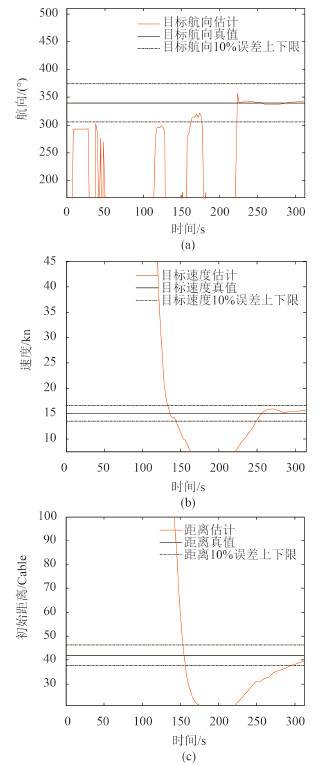
目标航向 340°,目标速度 15 kn,观测器运动要素以及波束域的目标音频信号的 LOFAR 谱图以及提取的线谱特征见图 6,其中 LOFAR 谱图采用 Welch 方法作时频分析得到。图 7 为上述算法解算的结果,从结果看,利用多普勒频移,在该态势下,目标速度和航向 5 min内收敛,目标初始距离的收敛时间多于5 min。
|
图 6 观测器航向、速度和多普勒线谱频移 Fig. 6 Time series of observer course, velocity and Doppler measurement frequency shift |
|
图 7 目标航向、速度和初始距离估计 Fig. 7 The estimated results of target course, velocity and original distance |
本文利用目标方位和线谱多普勒频移,通过建立2个独立的伪线性滤波器,给出了一种估计目标要素的方法。根据理论分析、数值仿真和海试数据验证,可以得到以下结论:
1)具有声吶设备的观测平台,可以不需要平台机动,能够得到一定精度的目标要素估计;
2)近距离目标与远距离目标相比,多普勒频移变化大,估计精度高;
3)方位误差和多普勒频移误差越大,估计收敛时间越长,目标航向的估计收敛时间短;
4)线谱频率的测量精度对参数估计结果影响显著,建立更先进的频率估计方法是进一步研究的方向之一。
| [1] | JAUFFRET C, PILLON D. Observability in passive target motion analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(4):1290-1300. |
| [2] |
杜选民, 姚蓝. 基于方位-频率及多阵方位的无源目标跟踪性能研究[J]. 声学学报, 2001, 26(2):127-134. DU Xuan-min, YAO Lan. Performance of passive target tracking using bearing-frequency and bearings of multiple arrays[J]. Acta Acustica, 2001, 26(2):127-134. |
| [3] |
胡青, 宫先仪. 方位/频率目标运动分析实验研究[J]. 声学学报, 2005, 30(2):120-124. HU Qing, GONG Xian-yi. Experimental research of bearing/frequency target motion analysis[J]. Acta Acustica, 2005, 30(2):120-124. |
| [4] | PASSERIEUX J M, PILLON D, BLANC-BENON P, et al. Target motion analysis with bearings and frequencies measurements via instrumental variable estimator[passive sonar] [C]//Proceedings of the International Conference on Acoustics, Speech, and Signal Processing. Glagow, UK:IEEE, 1989, 4:2645-2648. |
| [5] | 刘健, 刘忠, 玄兆林. 一种基于方位-频率测量的被动声呐TMA算法分析[J]. 声学与电子工程, 2005(4):1-3, 11. |
| [6] |
赵申东, 宋志杰. 基于方位和线谱频移的TMA方法[J]. 火力与指挥控制, 2004, 29(3):74-76. ZHAO Shen-dong, SONG Zhi-jie. Research of TMA based on bearings and line Doppler shift[J]. Fire Control & Command Control, 2004, 29(3):74-76. |
| [7] |
刘忠, 邓聚龙. 等速运动观测站纯方位系统的可观测性[J]. 火力与指挥控制, 2004, 29(6):51-54. LIU Zhong, DENG Ju-long. Observability analysis for single bearings-only observer traveling with constant velocity[J]. Fire Control & Command Control, 2004, 29(6):51-54. |
| [8] |
赵建昕. 二维运动目标纯方位系统的部分可观测性[J]. 情报指挥控制系统与仿真技术, 2005, 27(6):8-10. ZHAO Jian-xin. Part observability analysis in bearings-only system for two-dimentional moving target[J]. Information Command Control System & Simulation Technology, 2005, 27(6):8-10. |
| [9] |
赵建昕, 过武宏, 笪良龙, 等. 基于纯方位的浅海距离特征量解算分析[J]. 应用声学, 2015, 34(4):320-332. ZHAO Jian-xin, GUO Wu-hong, DA Liang-long, et al. Analysis of distance characteristic variable solved based on bearings-only in shallow sea[J]. Journal of Applied Acoustics, 2015, 34(4):320-332. |
 2016, Vol. 38
2016, Vol. 38
