随着水声技术的不断进步与发展,人类开展的水下活动日益频繁。无论在海洋资源勘探、海洋生物动态监测、水下定位导航等民用领域,还是在水下军事目标探测等军事领域,水下目标的高精度定位显得尤为重要[1, 2, 3]。目前常用的高精度水下目标被动定位方法主要采用大孔径基阵和特定的高分辨阵处理算法[4, 5, 6, 7, 8]。增大基阵孔径会增加工程实现难度,且基阵孔径过大,信号的空间相关性会下降,反而会降低探测精度。高分辨的阵处理算法稳健性较差,先验条件的不匹配会导致处理性能急剧下降。
针对以上问题,提出一种基于矢量水听器和小孔径标量圆形阵的高精度水下目标被动定位方法。将矢量水听器置于标量圆形阵的圆心处,综合利用标量阵常规波束形成的稳健性和矢量水听器的测向原理,可大幅提高目标的测向精度。并利用多个基阵进行空间方位交汇可对目标进行测距。当存在多个目标时,通过基阵两两组合进行“举手表决”剔除伪解的方法,还可分辨多个目标。最后通过仿真实验验证了方法的有效性。
1 矢量水听器测向原理矢量水听器利用 x,y 方向振速信号的正交性进行测向:
| $ \theta ={{\tan }^{-1}}\left( \frac{{{v}_{y}}}{{{v}_{x}}} \right) $ | (1) |
平面波声压振速有如下关系:
| $ v = \frac{p}{{\rho c}} $ | (2) |
假设阵元域声压信号为 s(t),噪声信号 n(t),则 x和y 方向的振速信号可表示为:
| $ {{v}_{y}}=\frac{s\left( t \right)\sin \theta +n\left( t \right)}{\rho c}, $ | (3) |
| $ {v_x} = \frac{{s\left( t \right)\cos \theta + n\left( t \right)}}{{\rho c}} $ | (4) |
噪声背景下矢量水听器测向表达式为:
| $ \hat{\theta }={{\tan }^{-1}}\left[\frac{\int{\left[s\left( t \right)\sin \theta +n\left( t \right) \right]\text{d}t}}{\int{\left[s\left( t \right)\cos \theta +n\left( t \right) \right]\text{d}t}} \right] $ | (5) |
单纯采用矢量水听器,阵元域信噪比较低时,测向精度较差。为提高测向精度,采用圆形阵与矢量水听器联合处理,通过圆形阵波束形成提高信噪比,并利用波束输出与矢量水听器输出的相关性进行测向,可大幅提高测向精度。
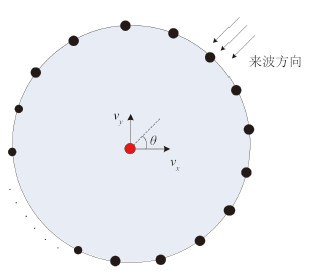
图 1 为联合处理基阵示意图,半径为 R 的圆周上均匀分布 N 个水听器,矢量水听器置于圆心处。该基阵可由下式进行测向:
|
图 1 基阵示意图 Fig. 1 Sketch map of array |
| $ \theta = {\tan ^{ - 1}}\left( {\frac{{\displaystyle\int {p{v_y}} }}{{\displaystyle\int {p{v_x}} }}} \right) $ | (6) |
在波束对准目标的情形下波束输出为:
| $ p\left( t \right) = Ns\left( t \right) + \sqrt N n\left( t \right) $ | (7) |
将波束输出信号 p(t)与矢量水听器两路输出 vv和vx 分别进行相关运算,结果用 Vv和Vx 表示,并利用两路信号的正交性进行测向,即
| $ \begin{align} & {{V}_{y}}=\left[ Ns\left( t \right)+\sqrt{N}n\left( t \right) \right]\frac{s\left( t \right)\sin \theta +n\left( t \right)}{\rho c}= \\ & \frac{N{{s}^{2}}\left( t \right)\sin \theta +\left( N+\sqrt{N}\sin \theta \right)s\left( t \right)n\left( t \right)+\sqrt{N}{{n}^{2}}\left( t \right)}{\rho c} \\ \end{align} $ | (8) |
| $ \begin{align} & {{V}_{x}}=\left[ Ns\left( t \right)+\sqrt{N}n\left( t \right) \right]\frac{s\left( t \right)\cos \theta +n\left( t \right)}{\rho c}= \\ & \frac{N{{s}^{2}}\left( t \right)\cos \theta +\left( N+\sqrt{N}\cos \theta \right)s\left( t \right)n\left( t \right)+\sqrt{N}{{n}^{2}}\left( t \right)}{\rho c} \\ \end{align} $ | (9) |
以上两式中第 1 项为信号成分,第 3 项为噪声成分,第 2 项为信号和噪声的互相关,由于信号和噪声相互独立,故交叉项可忽略不计,于是有:
| $ \hat \theta = {\tan ^{ - 1}}\left( {\frac{{\int {{V_y}} }}{{{{\int V }_x}}}} \right) = \frac{{\int {N{s^2}\left( t \right)\sin \theta + \sqrt N {n^2}\left( t \right)} }}{{\int {N{s^2}\left( t \right)\cos \theta + \sqrt N {n^2}\left( t \right)} }} $ | (10) |
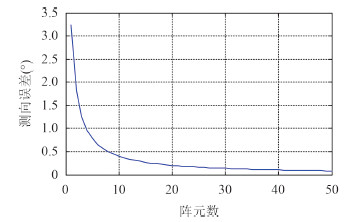
可见阵元数对测向精度有明显影响,图 2 为阵元域信噪比为 10 dB 时,阵元数对测向误差的影响情况。由图 2 可知,当 N < 10 时,随着阵元数的增大,测向误差从 5.4°降为 0.8°,对测向精度的改善作用很明显;当 N > 40 时,测向误差随阵元数增大缓慢减小,N = 50 时,误差为 0.2°。
|
图 2 测向误差与阵元数的关系 Fig. 2 Orientation error versus number of array element |
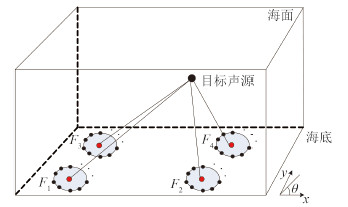
前文阐述了基阵的测向原理,利用 2 个或多个基阵进行方位交汇可对目标进行定位,如图 3 所示,坐标系规定如下:基阵编号 1,2,3,4,分别用 F1,F2,F3,F4 表示,以 F1 中心为坐标原点,x 轴为正东方向,y 轴为正北,4 个基阵的圆心坐标分别为(0,0,0),(a,0,0),(0,a,0)和(a,a,0),a>0,4 个圆心构成正方形的 4 个顶点。方位角 θ 为目标与圆心连线和x 轴构成的夹角,逆时针方向为正。
|
图 3 多基阵目标定位示意图 Fig. 3 Sketch map of target localization for mutiple array |
利用任意 2 个基阵进行方位交汇即可对目标进行二维定位,但随着基阵数量增多,定位精度随之提高。现将 2 个基阵定位原理简要阐述如下:
以 1 号和2 号阵为例,两者测得的目标方位分别为 θ1和θ2,假设目标与基阵圆心距离分别为 r1和r2,根据几何关系有下式:
| $ \left\{ \begin{align} & {{r}_{1}}\cos {{\theta }_{1}}-{{r}_{2}}\cos {{\theta }_{2}}=a\text{,} \ & {{r}_{1}}\sin {{\theta }_{1}}-{{r}_{2}}\sin {{\theta }_{2}}=0 \ \end{align} \right. $ | (11) |
通过上式可解算出距离值 r1和r2 分别为:
| $ {{r}_{1}}=\left| \frac{a\sin {{\theta }_{2}}}{\sin \left( {{\theta }_{2}}-{{\theta }_{1}} \right)} \right| $ | (12) |
| $ {r_2} = \left| {\frac{{a\sin {\theta _1}}}{{\sin \left( {{\theta _2} - {\theta _1}} \right)}}} \right| $ | (13) |
当存在 M 个目标时,目标编号为 1,2,…,M,每个基阵将解算出 M 个方位值,此时距离解算公式演变为:
| $ {{r}_{1ij}}=\left| \frac{L\sin {{\theta }_{2i}}}{\sin \left( {{\theta }_{2i}}-{{\theta }_{1j}} \right)} \right|,j=1\text{,}2...M $ | (14) |
| $ {{r}_{2ij}}=\left| \frac{L\sin {{\theta }_{1j}}}{\sin \left( {{\theta }_{2i}}-{{\theta }_{1j}} \right)} \right|,j=1,2...M $ | (15) |
式中:θ2i 为 2 号基阵 F2 对第 i 号目标的方位解算结果;θ1j 为基阵 F1 对第j 号目标的方位解算结果。此时基阵两两交汇可解算出 M2 个距离值,其中有 M 个为真值,其余为伪解。当 i = j时,2 个基阵对准同一目标,解算结果为真值。
针对这种情况,可通过基阵两两组合的方式进行“举手表决”选出真值,4 个基阵两两组合共有 6 种组合方式,每 2 个基阵组合均可解算出 M2个结果,则对每个结果投 1 票,6 种组合均解算完毕后,每组结果中必有 M 个结果重合,即这 M 个结果可得 6 票,而其余结果均低于 6 票,则得票最高的这 M 个解算结果为目标的最终位置。
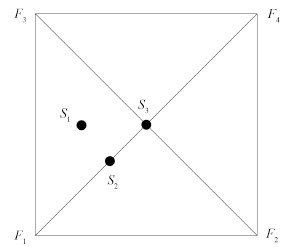
3 仿真算例目标声源有3 个目标,结合正方形区域的对称性,选取典型的 3 个位置 S1,S2,S3 进行分析,它们分别位于某一三角形中间、对角线上及中心位置,其平面示意图如图 4 所示。信号特征为:连续信号,频带 3~6 kHz,3 kHz 处谱级 140 dB,每倍频呈 6 dB 衰减,背景噪声 60 dB。
|
图 4 基阵和声源位置平面示意图 Fig. 4 Sketch map of position of array and sound source |
基阵参数为:半径 R = 1.2 m,阵元数 N = 50,设计频率 4 kHz,相邻基阵间距离 a= 5 km,4 个基阵构成一个边长 5 km 的正方形探测区域。
不考虑深度,基阵中心及目标声源位置坐标依次为 F1(0,0),F2(5 km,0),F3(0,5 km),F4(5 km,5 km),S1(1.25 km,2.5 km),S2(1.679 km,1.679 km),S3(2.5 km,2.5 km)。
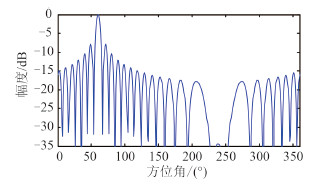
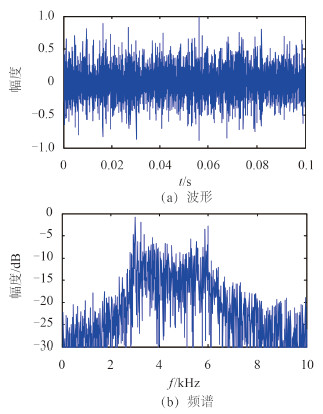
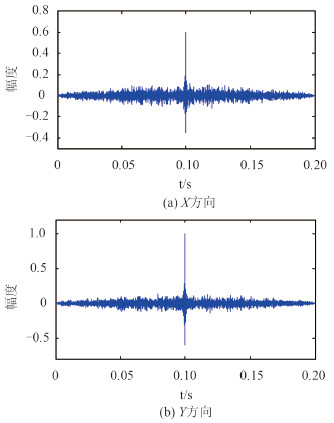
图 5 为圆形阵空间波束图,主瓣方向为 60°,主瓣宽度 7°,第 1 旁瓣高度 -8 dB。图 6 为信号源波形及频谱,图 7 为圆形阵和矢量水听器在 X 方向和 Y 方向的相关输出。根据测向公式解算的目标方位值为 59.2°,测向误差为 0.8°。相同条件下,单独采用圆形阵的测向误差为 3.5°,单独采用矢量水听器的误差为 4.0°。可见圆形阵和矢量水听器联合处理可大幅提高测向精度。
|
图 5 圆形阵波束图 Fig. 5 Beam pattern of circle array |
|
图 6 声源信号波形及频谱 Fig. 6 Waveform and spectrum of sound source |
|
图 7 圆形阵与矢量水听器相关输出 Fig. 7 Correlative output of circle array and vector hydrophone |
表 1 为 3 个目标声源的定位精度对比情况,为便于比较,这里采用柱坐标系。从表中可看出,S1 的测向精度为 0.8°,测距精度为 71 m,测距相对误差为2.5%;目标声源位于对角线上时,S2 测向精度为 1.0°,测距精度为 84 m,测距相对误差为 3.5%;目标声源位于阵中心时,S3 测向精度为 0.5°,测距精度为 34 m,测距相对误差为 1%;对比可看出,声源 S3 的定位精度最高,S1 精度次之,S2 精度最低,可见阵中心附近区域为最高精度定位区。总的来看,阵内声源的定位精度都很高,测向误差在 1°以内,测距相对误差也低于 5%。
|
|
表 1 不同位置的定位精度对比 Tab.1 Comparison of localization accuracy for sound source at different position |
本文提出一种基于矢量水听器和小孔径标量圆形阵的高精度水下目标被动定位方法。综合利用标量阵常规波束形成的稳健性和矢量水听器的测向原理,可大幅提高目标的测向精度。并利用多个基阵进行空间方位交汇可对多目标进行测距。仿真结果表明,在 4 个基阵围成的边长 5 km 的正方形探测区域内,3 个目标测向精度均在 1°以内,相对测距误差低于 5%。与目前常用的水下目标高精度被动定位方法相比,本文优势主要是:一是基阵孔径小,大幅降低了系统成本和工程实践难度;二是综合利用了标量水听器阵常规波束形成的稳健性和矢量水听器测向精度高的优点,既保证了定位精度,又不失稳健性;三是通过基阵两两组合进行“举手表决”剔除伪解的方法,可分辨多个目标。
| [1] | 毛卫宁. 水下被动定位方法回顾与展望[J]. 东南大学学报(自然科学版), 2001, 31(6):129-132. |
| [2] | THOMSON D, ELSON S. New generation acoustic positioning systems[C]//Proceedings of Oceans'02 MTS/IEEE. Biloxi, MI, USA:IEEE, 2002:1312-1318. |
| [3] | 曾林志, 徐国华, 徐兵, 等. 水下试验平台高精度定位系统研究[J]. 中国机械工程, 2014, 25(8):1021-1027. |
| [4] | BISWAS P, LIAN T C, WANG T C, et al. Semidefinite programming based algorithms for sensor network localization[J]. ACM Transactions on Sensor Networks, 2006, 2(2):188-200. |
| [5] | 张同伟, 杨坤德, 马远良, 等. 一种基于单水听器宽带信号自相关函数的水下目标定位稳健方法[J]. 物理学报, 2015, 24(3):280-286. |
| [6] | 杨道军, 许伟杰, 刘林泉, 等. 高精度定位标定系统水下基准方位误差分析[J]. 声学技术, 2007, 26(2):189-192. |
| [7] | 刘流, 孟彧仟, 张自丽, 等. 双基阵节点被动测距方法实验研究[J]. 舰船电子工程, 2015, 35(4):63-64, 120. |
| [8] | 徐本连, 董学平, 王执铨. 双基阵纯方位目标跟踪的抗野值算法研究[J]. 东南大学学报(自然科学版), 2004, 34(S):199-203. |
 2016, Vol. 38
2016, Vol. 38
