目前,长航时潜器水下自主导航主要依靠推算导航与惯性导航[1],但2种导航方式都存在定位误差随时间积累的缺点,当前水下隐蔽定位修正比较实用的是水声定位方法,因此,国内外在水声定位系统辅助潜器定位方面进行了大量研究,如文献[2]将测距声信标与载体低成本导航传感器的导航数据相融合,提出基于 EKF 的导航数据融合算法,解决复杂环境下的深水机器人位置估计问题。文献[3, 4]研究了基于移动长基线的 AUV 协同导航算法。文献[5, 6]研究了只依靠航迹推算和潜器之间相对测距的情况下,潜器的相对定位问题。文献[7, 8]则针对移动长基线 AUV 协同导航中的水声传播延迟误差进行分析,并给出补偿方法。然而这些研究的前提都是 AUV 上不装备惯导系统,只装备简单的导航设备,系统模型则为 AUV 运动学模型。而随着大型远程 AUV 的发展,以及其他潜器惯导系统水下校正的需求日益迫切,针对惯导/水声测距组合导航的研究具有重要意义。本文以惯导系统误差模型为基础,提出惯导/多信标测距组合导航实现方法,用于潜器惯导定位误差修正,并主要针对由于潜器运动及水声传播时间延迟导致的误差进行分析及补偿方法研究。
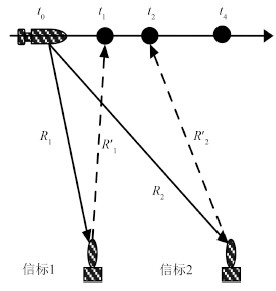
1 时间延迟误差分析由于水声信号在水中传播速度较慢1500 m/s,而潜器处于运动状态,因此必须考虑时间延迟导致的误差。如图 1 所示,潜器发送 Ping 询问信号后收到信标的应答信号需要一定的时间。同时,由于潜器与各信标之间的距离不等,潜器收到每个信标应答信号的时刻也不相同,加上潜器的自身运动,因而潜器在不同位置不同时刻收到信标应答信号。文献[7]对此进行分析,但存在问题,下面给出详细分析。
|
图 1 时间延迟误差示意图 Fig. 1 Schematic diagram of the time-delay error |
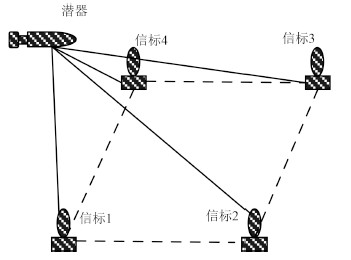
通常长基线定位系统布放 4 个信标,如图 2 所示。若不考虑时间延迟,根据长基线定位原理,可得潜器与信标 1 之间的定位方程如下[9]:
|
图 2 长基线定位系统 Fig. 2 The LBL positioning system |
| $ {(x - {x_{b1}})^2} + {(y - {y_{b1}})^2} + {(z - {z_{b1}})^2} = R_1^2 $ | (1) |
其中x,y,z为潜器在阵位坐标系下的位置坐标。此处,阵位坐标系原点设在信标 1 所在位置,坐标轴指向与东北天地理坐标系相同。
在阵位坐标系下,潜器从 t0 时刻发出 Ping 到应答器收到应答信号用时为 $\Delta {T_1}$,其中询问信号传播时间 $\Delta {t_1}$,应答信号传播时间 $\Delta {t_2}$,其间潜器定深航行位移为 $\Delta {S_1} = (\Delta {x_1},\Delta {y_1})$。考虑到惯导具有较高的短时相对精度,该位移可由惯导输出速度进行推算。从而可得方程
| $ \begin{gathered} \sqrt {{{({x_{{t_0}}} - {x_{b1}})}^2} + {{({y_{{t_0}}} - {y_{b1}})}^2} + {{(z - {z_{b1}})}^2}} = C \cdot \Delta {t_1} \hfill \\ \sqrt {{{({x_{{t_0}}} + \Delta {x_1} - {x_{b1}})}^2} + {{({y_{{t_0}}} + \Delta {y_1} - {y_{b1}})}^2} + {{(z - {z_{b1}})}^2}} = C \cdot \Delta {t_2} \hfill \\ \end{gathered} $ | (2) |
上式两边平方并相加
| $ \begin{gathered} {({x_{{t_0}}} - {x_{b1}})^2} + {({y_{{t_0}}} - {y_{b1}})^2} + 2{(z - {z_{b1}})^2} + {({x_{{t_0}}} + \Delta {x_1} - {x_{b1}})^2} \hfill \\ + {({y_{{t_0}}} + \Delta {y_1} - {y_{b1}})^2} = {(C\Delta {t_1})^2} + {(C\Delta {t_2})^2} \hfill \\ \end{gathered} $ | (3) |
整理为
| $ \begin{gathered} {({x_{{t_0}}} + \frac{1}{2}\Delta {x_1} - {x_{b1}})^2} + {({y_{{t_0}}} + \frac{1}{2}\Delta {y_1} - {y_{b1}})^2} + {(z - {z_{b1}})^2} = \hfill \\ \frac{1}{2}{C^2}(\Delta {t_1}^2 + \Delta {t_2}^2) - \frac{1}{4}\Delta x_1^2 - \frac{1}{4}\Delta y_1^2 \hfill \\ \end{gathered} $ | (4) |
对于等式右边,令 $\Delta {t_1} \approx \Delta {t_2} = \displaystyle\frac{1}{2}\Delta {T_1}$,则有
| $ \begin{gathered} {({x_{{t_0}}} + \frac{1}{2}\Delta {x_1} - {x_{b1}})^2} + {({y_{{t_0}}} + \frac{1}{2}\Delta {y_1} - {y_{b1}})^2} + {(z - {z_{b1}})^2} = \hfill \\ {(\frac{1}{2}C\Delta {T_1})^2} - \frac{1}{4}\Delta x_1^2 - \frac{1}{4}\Delta y_1^2 = R_1^2 - \frac{1}{4}\Delta x_1^2 - \frac{1}{4}\Delta y_1^2 \hfill \\ \end{gathered} $ | (5) |
值得指出的是,上述推导过程中的声速 C 为水声系统利用水声传播特性相关理论进行修正过的声速,即 R1 为水声系统输出的距离量测值。
记由 $({x_{b1}} - \frac{1}{2}\Delta {x_1}{\text{,}}{y_{b1}} - \frac{1}{2}\Delta {y_1}{\text{,}}{z_{b1}})$ 坐标所确定的点为伪信标 1,$\sqrt {R_1^2 - \displaystyle\frac{1}{4}\Delta x_1^2 - \frac{1}{4}\Delta y_1^2} $ 为潜器与伪信标 1 的伪距。同理可得潜器与其他伪信标之间的伪距方程。根据长基线定位原理,可计算潜器在 t0 时刻的位置${t_0}$,${y_{{t_0}}}$。可见,使用球面相交法求得的解并非潜器完全收到应答信号时的位置,而是潜器发出 Ping 时刻的位置,从而产生时间延迟误差。该误差量可表示为
| $ E = \frac{{2 \cdot \max ({R_1}{\text{,}}{R_2}{\text{,}}{R_3}{\text{,}}{R_4}) \cdot V}}{C} $ | (6) |
可见误差大小与潜器到各信标的距离 R 及潜器航速 V 有关,距离越远,航速越大,则误差越大。显然,若用此位置作为 t4 时刻的潜器位置来估计惯导位置误差,则相当于附加了一个大小为 E 的误差量,从而产生位置误差估计误差。
2 考虑水声传播时间延迟的惯导定位误差修正算法 2.1 系统方程在本系统中,深度 z 可由深度传感器直接获取,故误差模型中不考虑 z 方向速度误差及深度 z 的误差。
选取状态变量X=[α β γ δVX δVY δL δλ]T,可根据捷联惯导系统误差模型写出系统方程
| $ \dot X = F \cdot \dot X + w $ | (7) |
系统矩阵 F 及 w的具体形式见文献[10]。
2.2 重构量测方程由前述推导,可得量测方程(以信标 1 为例)
| $ R=\sqrt{\begin{align} & {{({{x}_{{{t}_{0}}}}+\frac{1}{2}\Delta {{x}_{1}}-{{x}_{b1}})}^{2}}+{{({{y}_{{{t}_{0}}}}+\frac{1}{2}\Delta {{y}_{1}}-{{y}_{b1}})}^{2}} \\ & +{{(z-{{z}_{b1}})}^{2}}+\frac{1}{4}\Delta x_{1}^{2}+\frac{1}{4}\Delta y_{1}^{2} \\ \end{align}} $ | (8) |
为补偿时间延迟造成的误差,重构量测方程。
潜器在 t0 时刻的位置状态可由 t4 时刻位置向前推求得
| $ \begin{array}{*{20}{c}} {{x_{{t_0}}} = {x_k} - \Delta {x_4}{\text{,}}} \ {{y_{{t_0}}} = {y_k} - \Delta {y_4}} \end{array} $ | (9) |
其中,Δx4,Δy4为潜器从 t0 时刻到 t4 时刻的航行位移,xk,yk是 t4 时刻真实位置。
设 $\left( {\delta x,\delta y} \right)$ 为 t4 时刻惯导输出位置与真实位置之间的误差,则有
| $ {x_{Ik}} = {x_k} + \delta x{\text{,}}{y_{Ik}} = {y_k} + \delta y $ | (10) |
代入上式有
| $ \begin{array}{*{20}{c}} {{x_{{t_0}}} = {x_{Ik}} - x - \Delta {x_4}{\text{,}}} \ {{y_{{t_0}}} = {y_{Ik}} - y - \Delta {y_4}} \end{array} $ | (11) |
以 $R$ 为量测量,可得 EKF 的量测方程,
| $ \begin{array}{*{35}{l}} \begin{align} & {{Z}_{k}}=h(\delta x,\delta y)+{{v}_{z}} \\ & =\sqrt{\begin{array}{*{35}{l}} \begin{align} & {{({{x}_{Ik}}-\delta x-\Delta {{x}_{4}}-{{x}_{bi}}+\frac{1}{2}\Delta {{x}_{i}})}^{2}}+ \\ & {{({{y}_{Ik}}-\delta y-\Delta {{y}_{4}}-{{y}_{bi}}+\frac{1}{2}\Delta {{y}_{i}})}^{2}} \\ & +{{(z-{{z}_{bi}})}^{2}}+\frac{1}{4}\Delta x_{i}^{2}+\frac{1}{4}\Delta y_{i}^{2}\text{,} \\ \end{align} \\ \end{array}} \\ & +{{v}_{z}}\ i=1\text{,}\cdots \text{,}4 \\ \end{align} \\ \end{array} $ | (12) |
式中:${v_z}$ 为量测噪声,设为独立且不相关的零均值高斯白噪声,其方差为
| $ E({v_z}v_z^{\text{T}}) = \left[{\begin{array}{*{20}{c}} {\sigma _{P_1^2}^2}&0&0&0 \ 0&{\sigma _{P_2^2}^2}&0&0 \ 0&0&{\sigma _{P_3^2}^2}&0 \ 0&0&0&{\sigma _{P_4^2}^2} \end{array}} \right] $ | (13) |
量测方程的雅克比矩阵为
| $ H_k^z = {\left. {\frac{{\partial h}}{{\partial {X_k}}}} \right|_{{{\hat X}_{k{\text{,}}k - 1}}}} = \left[{\begin{array}{*{20}{c}} {{e_{1x}}}&{{e_{1y}}} \ {{e_{2x}}}&{{e_{2y}}} \ {{e_{3x}}}&{{e_{3y}}} \ {{e_{4x}}}&{{e_{4y}}} \end{array}} \right] $ | (14) |
其中,
$ {e_{jx}} = \frac{{ - ({x_{Ik}} - \delta {{\hat x}_{k,k - 1}} - \Delta {x_4} - {x_{bj}} + \frac{1}{2}\Delta {x_j})}}{{\hat \rho {\text{ }}_{k,k - 1}^j}} $
$ {e_{jx}} = \frac{{ - ({x_{Ik}} - \delta {{\hat x}_{k,k - 1}} - \Delta {x_4} - {x_{bj}} + \frac{1}{2}\Delta {x_j})}}{{\hat \rho _{k,k - 1}^j}} $
$ \hat{\rho }_{k,k-1}^{j}=\sqrt{\begin{array}{*{35}{l}} \begin{align} & {{({{x}_{Ik}}-\delta {{{\hat{x}}}_{k\text{,}k-1}}-\Delta {{x}_{4}}-{{x}_{bj}}+\frac{1}{2}\Delta {{x}_{j}})}^{2}}+\ \\ & {{({{y}_{Ik}}-\delta {{{\hat{y}}}_{k\text{,}k-1}}-\Delta {{y}_{4}}-{{y}_{bj}}+\frac{1}{2}\Delta {{y}_{j}})}^{2}}+{{(z-{{z}_{bj}})}^{2}} \\ & +\frac{1}{4}\Delta x_{j}^{2}+\frac{1}{4}\Delta y_{j}^{2} \\ \end{align} \\ \end{array}} $
由 $\left[{\begin{array}{*{20}{c}} {\delta x} \\ {\delta y} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {0}&{{R_e} \cdot \cos L} \\ {{R_e}}&{0} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {\delta L} \\ {\delta \lambda } \end{array}} \right] = B_n^z\left[{\begin{array}{*{20}{c}} {\delta L} \\ {\delta \lambda } \end{array}} \right]$ ,可得系统量测矩阵为
| $ {H_k} = [{O_{4 \times 5}}\;\;H_k^z \cdot B_n^z] $ | (15) |
为验证算法的有效性,进行仿真试验。在仿真试验中,在水下 500 m 深度布放 4 个浮标,组成 4 000 m × 2 000 m 的长方形基阵。潜器直线航行,速度 2 m/s,航向 90°,深度 50 m。潜器 SINS 数据更新周期为 1 s。其中惯性元件参数如表 1 所示。
|
|
表 1 SINS误差源参数 Tab.1 SINS error source parameters |
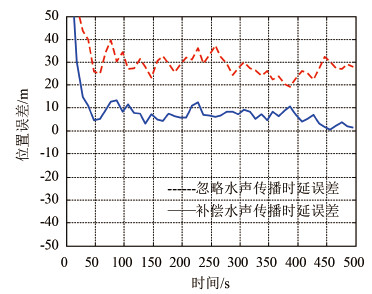
在进入信标作用范围之前,SINS 导航误差为:纬度误差-200 m,经度误差 200 m,失准角为2′,2′,1′。信标 1 位置为 L = 30°,λ = 120°。潜器开始发射第1个 Ping 信号的位置在阵位坐标系中表示为-2 000 m,1 000 m,潜器每隔 10 s 向外发送一次 Ping 询问信号,完全收到各信标的应答信号后进行惯导定位误差解算。修正过程持续 500 s。位置误差曲线如图 3 所示。
|
图 3 惯导定位误差曲线 Fig. 3 INS positioning error curve |
由图 3 可以看出,如果不进行水声传播时延误差补偿,则经过水声测距修正后,惯导定位误差仍然超过 30 m,采用本文方法进行补偿后,定位精度可达到 10 m 以内。可见,本文方法可有效补偿潜器运动和水声传播时延带来的误差。
4 结语本文提出惯导/多信标测距组合导航实现方法,用于潜器惯导定位误差修正,并主要针对由于潜器运动及水声传播时间延迟导致的误差进行分析,并给出补偿方法。即利用潜器在一个 Ping 采样周期内,惯导短时相对精度较高的特点,通过对惯导位置误差状态的前推,重构量测方程,与量测信息时间匹配,以修正时间延迟造成的误差。最后进行数学仿真,验证了方法的有效性。
| [1] |
刘芙蓉, 陈辉. 自主式水下潜器研究开发综述[J]. 舰船科学技术, 2008, 30(5):20-23. LIU Fu-rong, CHEN Hui. A review of the development and research of autonomous underwater vehicles[J]. Ship Science and Technology, 2008, 30(5):20-23. |
| [2] |
冀大雄, 刘健, 周波, 等. 深水机器人低成本导航系统的位置估计方法研究[J]. 仪器仪表学报, 2009, 30(1):35-38. JI Da-xiong, LIU Jian, ZHOU Bo, et al. Position estimation method for deep water vehicle using low-cost navigation sensors[J]. Chinese Journal of Scientific Instrument, 2009, 30(1):35-38. |
| [3] |
张立川, 徐德民, 刘明雍. 双伪测量的多水下航行器移动长基线协同导航算法[J]. 火力与指挥控制, 2013, 38(1):34-36. ZHANG Li-chuan, XU De-min, LIU Ming-yong. Cooperative navigation method of multiple autonomous underwater vehicles based on double acoustic measurement[J]. Fire Control & Command Control, 2013, 38(1):34-36. |
| [4] |
张福斌, 马朋. 一种基于虚拟移动长基线的多AUV协同导航算法[J]. 鱼雷技术, 2013, 21(2):115-119. ZHANG Fu-bin, MA Peng. A cooperative navigation algorithm of multiple AUVs based on synthetic moving long baseline[J]. Torpedo Technology, 2013, 21(2):115-119. |
| [5] | ENGEL R, KALWA J. Relative positioning of multiple underwater vehicles in the GREX project[C]//Proceedings of the 2009-EUROPE Oceans. Bremen:IEEE, 2009:1-7. |
| [6] | WOITHE H C, KREMER U. Using slocum gliders for coordinated spatial sampling[C]//Proceedings of the 2011 IEEE-Spain Oceans. Santander:IEEE, 2011:1-8. |
| [7] |
刘明雍, 黄博, 蔡挺. 一种基于量测伪距的EKF移动长基线AUV协同导航方法[J]. 鱼雷技术, 2012, 20(6):432-436. LIU Ming-yong, HUANG Bo, CAI Ting. A cooperative navigation method of EKF moving long baseline for AUV based on pseudo-range measurements[J]. Torpedo Technology, 2012, 20(6):432-436. |
| [8] |
高伟, 杨建, 刘菊, 等. 基于水声通信延迟的多UUV协同定位算法[J]. 系统工程与电子技术, 2014, 36(3):539-545. GAO Wei, YANG Jian, LIU Ju, et al. Cooperative location of multiple UUVs based on hydro-acoustic communication delay[J]. Systems Engineering and Electronics, 2014, 36(3):539-545. |
| [9] |
陈云飞, 李桂娟, 贾兵, 等. 水下合作目标三维定位技术[J]. 舰船科学技术, 2010, 32(5):48-51. CHEN Yun-fei, LI Gui-juan, JIA Bing, et al. Underwater cooperate target 3D positioning[J]. Ship Science and Technology, 2010, 32(5):48-51. |
| [10] |
葛锡云, 申高展, 潘琼文, 等. 基于惯性导航/地磁的水下潜器组合导航定位方法[J]. 舰船科学技术, 2014, 36(11):120-124. GE Xi-yun, SHEN Gao-zhan, PAN Qiong-wen, et al. The underwater integrated navigation method of underwater vehicle based on INS/geomagnetic[J]. Ship Science and Technology, 2014, 36(11):120-124. |
 2016, Vol. 38
2016, Vol. 38
