推进轴系被广泛应用在舰艇、船舶等诸多航行体的机械系统中。由于加工、安装及结构连接等误差,航行体的两转轴轴线会交叉成一定角度,即轴系的偏角不对中,不对中亦称偏斜。偏角与转轴的偏心因素耦合,使轴系在匀速运动过程中产生非线性激励,引起航行体壳体振动进而成为巨大的声辐射体,将会影响舰艇等作战平台的作战能力。研究偏角不对中轴系的振动特性可为提高航行体的声学性能奠定理论分析依据。在不对中转子系统非线性振动研究方面,李明等[1]通过利用数值算法求解平行不对中转子系统的动力学模型,获得不对中转子系统的非线性动力学行为,表明了不对中转子系统是一个具有自激振动特征的强非线性系统。黄典贵等[2]分析比较了平行不对中与交角不对中转子系统的扭转振动特征,同时研究了平行不对中和不平衡共存时故障转子的扭振特征。文献[3]针对偏角不对中情形,研究了偏斜轴系的分叉与混沌振动特征,表明了偏斜因素作用下轴系振动及其特性分析的复杂性。Xu,Marangoni 等[4, 5]考虑了大角度偏斜,使用有限元法、模态综合法简化计算,比较全面地分析了由不对中力矩激起的偶数倍共振的多次谐波成份,并进行了相应的实验研究。Al-Hussain 等[6, 7]进行了刚性连接平行不对中转子横向与扭转振动响应的数值分析,指出稳定条件下平行不对中是扭转和横向振动的激励源,并利用 Liapunov 指数法给出了偏角和联轴器刚度对系统稳定区域的影响规律。文献[8]表明鱼雷等水下航行体的辐射噪声主要来源于壳体内部机械部件运动以及结构振动形成的机械噪声,简称结构(辐射)噪声。由国内外研究现状可知,不对中因素会导致轴系产生复杂的非线性振动,会成为舰艇噪声辐射的重要声源。
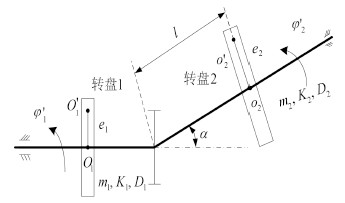
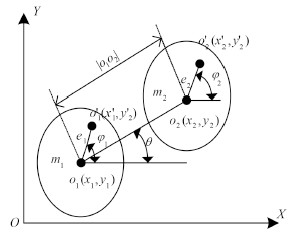
1 动力学模型文献[3]考虑了轴承油膜、局部碰摩等因素的耦合作用,建立了不对中轴系横向振动方程,本文忽略了油膜和碰摩因素,仅考虑存在偏角不对中的不平衡轴系,假定转轴的质量集中在位于刚性联轴器相连两转轴的横跨中心的转盘上,从动轴 o2 绕主动轴 o1 同步转动(见图 1)。设转盘的初始旋转速度 ${{\varphi }_{0‘}}$,在轴系的静平衡位置,建立固定坐标系 $o-xy$ 如图 2 所示(假设不对中偏角量 α 为一小量,图中 α 被放大),转盘 1 的坐标位置为 ${{O}_{1}}\left( {{x}_{1}},{{y}_{1}} \right)$ ,质心坐标位置为 $O_1^\prime(x_1^\prime,y_1^\prime)$,质量 m1 ,偏心距 e1 ,与 x 轴夹角 ${{\varphi }_{1}}$ ;转盘 2 的坐标位置为 ${O_2}({x_2},{y_2})$,质心坐标位置为 $O_2^\prime(x_2^ \prime,y_2^ \prime)$,质量 m2 ,偏心距 e2 ,与 x 轴夹角 ${{\varphi }_{2}}$,l 为转轴 2 长度的一半。将转轴刚度、阻尼等效到转盘处,K1 、K2 、D1 、D2 为转盘处轴的等效刚度与阻尼。
|
图 1 偏角不对中轴系动力学模型 Fig. 1 The dynamical model of shafting with angular misalignment |
|
图 2 轴系坐标系 Fig. 2 Coordinate systems of the shafting |
为简化问题的讨论,假设:1)两转子均为刚性转子,不考虑轴系的轴向振动,转动过程中不存在陀螺效应;2)转轴刚性连接,两转轴同步旋转;3)仅存在偏角不对中,且不对中量为一小量;4)轴承各向同性,转轴的径向支承近似为短轴承。
由于存在偏角不对中,从动轴的质心坐标可表示为
| $\left\{ \begin{align} & {{x}_{c2}}=\left( {{x}_{2}}+{{e}_{2}} \right)\cos \alpha \\ & {{y}_{c2}}=\left( {{y}_{2}}+{{e}_{2}} \right)\cos \alpha \\ \end{align} \right.$ | (1) |
又由基本假设可得两转轴的运动约束方程为
| $\begin{align} & f({{x}_{1}},{{y}_{1}},{{x}_{2}},{{y}_{2}})= \\ & {{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}-{{(l\sin \alpha )}^{2}}=0 \\ \end{align}$ | (2) |
由分析力学理论知,式(1)为一完整约束。利用 Lagrange 待定乘子$\lambda $ 表示的系统振动方程为
| $\left\{ \begin{align} & {{m}_{1}}{{{\ddot{x}}}_{1}}+{{K}_{1}}{{x}_{1}}+{{D}_{1}}{{{\dot{x}}}_{1}}= \\ & {{m}_{1}}{{e}_{1}}\left( {{\left( \varphi {{'}_{1}} \right)}^{2}}\cos {{\phi }_{1}}+\varphi _{_{1}}^{,,}\sin {{\varphi }_{1}} \right)+\lambda ({{x}_{1}}-{{x}_{2}}) \\ & {{m}_{1}}{{{\ddot{y}}}_{1}}+{{K}_{1}}{{y}_{1}}+{{D}_{1}}{{{\dot{y}}}_{1}}= \\ & {{m}_{1}}{{e}_{1}}\left( {{\left( \varphi {{'}_{1}} \right)}^{2}}\sin {{\phi }_{1}}-\varphi _{_{1}}^{,,}\cos {{\varphi }_{1}} \right)-{{m}_{1}}g+\lambda ({{y}_{1}}-{{y}_{2}}) \\ & {{m}_{2}}{{{\ddot{x}}}_{2}}+{{K}_{2}}{{x}_{2}}+{{D}_{2}}{{{\dot{x}}}_{2}}= \\ & {{m}_{2}}{{e}_{2}}\cos \alpha \left( {{\left( \varphi {{'}_{2}} \right)}^{2}}\cos {{\varphi }_{2}}+\varphi _{_{2}}^{,,}\sin {{\varphi }_{2}} \right)+\lambda ({{x}_{2}}-{{x}_{1}}) \\ & {{m}_{2}}{{{\ddot{y}}}_{2}}+{{K}_{2}}{{y}_{2}}+{{D}_{2}}{{{\dot{y}}}_{2}}= \\ & {{m}_{2}}{{e}_{2}}\cos \left( \alpha {{\left( \varphi {{'}_{2}} \right)}^{2}}\sin {{\varphi }_{2}}-\varphi _{_{2}}^{,,}\cos {{\varphi }_{2}} \right)-{{m}_{2}}g+\lambda ({{y}_{2}}-{{y}_{1}}) \\ \end{align} \right.$ | (3) |
由于采用刚性联轴器及两转子同步匀速旋转,则有 ${\varphi' _1} = {\varphi' _2}$ 且 ${\varphi'' _1} = {\varphi'' _2}$,其中记 $\left( {} \right)' = d\left( {} \right)/d\tau $,$\left( {} \right)'' = d\left( {} \right)/d{\tau ^2}$。设转盘 1 的初始旋转速度 ${\varphi _0''}$,则
转盘1的旋转角度为
| ${\varphi _1} = {\varphi _0'}t$ | (4) |
转盘 2 的旋转角度为
| ${\varphi _2} = {\varphi' _0}t + {\varphi _0}$ | (5) |
取轴颈平均间隙 cz = 0.2 mm,定义无量纲参数如下:
| ${\omega _{n1}} = \sqrt {\frac{{{K_1}}}{{{m_1}}}} ,\tau = {\omega _{n1}}t{\text{,}}{\omega _{n2}} = \sqrt {\frac{{{K_2}}}{{{m_1}}}} {\text{,}}\eta = \frac{{{\omega _{n2}}}}{{{\omega _{n1}}}}$ |
| $\omega = {\text{ }}\frac{{{\varphi'' _1}}}{{{\omega _{n1}}}},m' = \frac{{{m_2}}}{{{m_1}}}{\text{,}}\varepsilon = \frac{{{e_1}}}{{{c_z}}}{\text{,}}{e'_2} = \frac{{{e_2}}}{{{c_z}}}{\text{,}}\bar l = \frac{l}{{{c_z}}}$ |
| ${c_1} = \frac{{{D_1}}}{{\sqrt {{K_1}{m_1}} }},{c_2} = \frac{{{D_2}}}{{\sqrt {{K_1}{m_1}} }},{X_1} = \frac{{{x_1}}}{{{c_z}}},{Y_1} = \frac{{{y_1}}}{{{c_z}}},$ |
| ${X_2} = \frac{{{x_2}}}{{{c_z}}},{Y_2} = \frac{{{y_2}}}{{{c_z}}},\gamma = \frac{\lambda }{{{m_1}\omega _{n1}^2}},\bar g = \frac{g}{{\omega _{n1}^2{c_z}}},$ |
则轴系无量纲化振动方程为
| $\left\{ \begin{gathered} X_{_1}^{,,} + {X_1} + {\zeta _1}X{'_1} = \hfill \\ {\varepsilon _1}{\omega ^2}\cos {\varphi _1} + \gamma ({X_1} - {X_2}),\hfill \\ Y_{_1}^{,,} + {Y_1} + {\zeta _1}{Y_1} = \hfill \\ {\varepsilon _1}{\omega ^2}\sin {\varphi _1} - \bar g + \gamma ({Y_1} - {Y_2}),\hfill \\ m'X_{_2}^{,,} + {\eta ^2}{X_2} + {c_1}X{'_2} = \hfill \\ m'{\varepsilon _2}{\omega ^2}\cos {\varphi _2}\cos \alpha + \gamma ({X_2} - {X_1}),\hfill \\ m'Y_{_2}^{,,} + {\eta ^2}{Y_2} + {c_1}Y{'_2} = \hfill \\ m'{\varepsilon _2}{\omega ^2}\sin {\varphi _2}\cos \alpha - m'\bar g + \gamma ({Y_2} - {Y_1}) \hfill \\ \end{gathered} \right.$ | (6) |
| ${({X_1} - {X_2})^2} + {({Y_1} - {Y_2})^2} = {(\bar l\sin \alpha )^2}$ | (7) |
由式(6)设
| $\left\{ \begin{gathered} {X_2} = {X_1} + \bar l\sin \alpha \cos \theta ,\hfill \\ {Y_2} = {Y_1} + \bar l\sin \alpha \sin \theta ,\hfill \\ \end{gathered} \right.$ | (8) |
联立式(6)与式(8)消除 Lagrange 待定乘子 γ,可得轴系的运动微分方程的矩阵形式为
| $M{u^{,,}} + Du' + Ku = {F_0} + {F_\varepsilon } + {F_\varphi } + {F_m},$ | (9) |
为求解该非定常二阶常微分方程,将式(9)两端同时左乘 M-1 ,经整理后将轴系的动力学方程表示为
| ${u^{,,}} = {M^{ - 1}}({F_0} + {F_e} + {F_\phi } + {F_m} - Du{,^,} - Ku) $ | (10) |
| $K = \left[{\begin{array}{*{20}{c}} {1 + {\eta ^2}}&0&0 \\ 0&{1 + {\eta ^2}}&0 \\ { - {\eta ^2}\sin \theta }&{{\eta ^2}\cos \theta }&0 \end{array}} \right],$ |
| $D = \left[{\begin{array}{*{20}{c}} {{c_1} + {c_2}} & 0 & { - {c_2}\bar l\sin \alpha \sin \theta }\\ 0 & {{c_1} + {c_2}} & {{c_2}\bar l\sin \alpha \cos \theta }\\ { - {c_2}\sin \theta } & {{c_2}\cos \theta } & 0 \end{array}} \right] ,$ |
| ${F_m} = \left[\begin{gathered} - 0 \hfill \\ (1 + m')\bar g \hfill \\ m{\text{'}}\bar g\cos \theta ,\hfill \\ \end{gathered} \right]$ |
| ${F_\varepsilon } = \left[{\begin{array}{*{20}{c}} {{\varepsilon _1}{\omega ^2}\cos {\varphi _1} + \bar m{\varepsilon _2}\cos \alpha {\omega ^2}\cos {\varphi _2}} \\ {{\varepsilon _1}{\omega ^2}\sin {\varphi _1} + \bar m{\varepsilon _2}\cos \alpha {\omega ^2}\sin {\varphi _2}} \\ {\bar m{\varepsilon _2}\cos \alpha ({\omega ^2}\sin {\varphi _2}\cos \theta - {\omega ^2}\cos {\varphi _2}\sin \theta )} \end{array}} \right]$ |
由于轴系受偏角不对中和转轴偏心因数影响,式(1)中存在许多非线性耦合项会导致复杂的振动响应,说明这是一个具有强非线性的三自由度系统。
2 算例分析采用 Runge-Kutta 法对非定常二阶常微分方程式(9)进行数值积分,分析系统振动响应形式及不对中偏角量、转轴质量比和主动轴无量纲转速对偏角不对中轴系匀速过程横向振动特性的影响。计算时取初始角位移 ${\varphi _0} = 0$,文中均以水平方向 X 的横向振动特性为研究对象。
1)偏角不对中量 α 对系统振动特性的影响
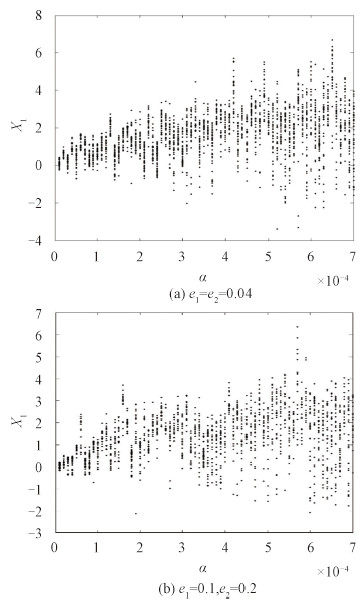
分析m'=0.8 ,$\alpha = 1 \times {10^{ - 5}}~7 \times {10^{ - 4}}$ 时,轴系的振动特性。
由图 3 可知:当 ω=0.8 时,在α=1×10-5~7×10-4 范围内,Poincare 截面上呈现为模糊一片的散点集,说明轴系响应存在概周期运动和混沌运动。随着不对中偏角量的变化,系统振动幅值较大且无明显变化规律。而从3(a)和3(b)可知,轴系偏心量的变化并不能改变轴系振动响应形式,对轴系振动的影响不明显。
|
图 3 ω = 0.8, m' = 0.8时,无量纲位移X1 的分岔图 Fig. 3 The bifurcation diagrams of X1 for ω= 0.8, $\bar m$= 0.8 |
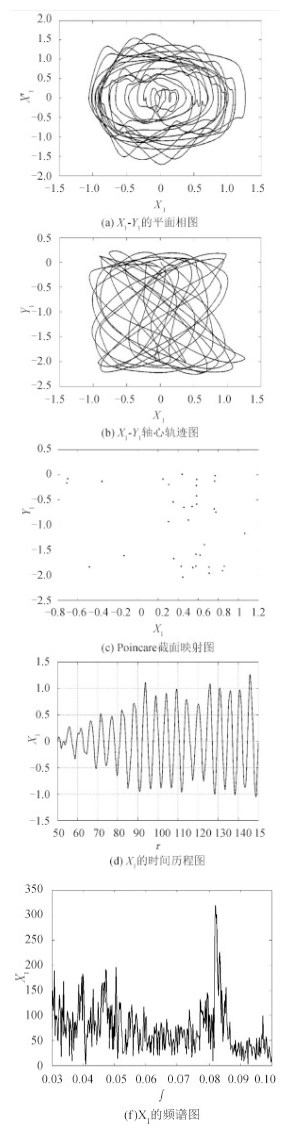
由系统响应的平面相图 4(a)和轴心轨迹图 4(b)可知,系统响应存在概周期运动和混沌运动,表现为相轨迹为局限于有界区域内的复杂不封闭曲线。Poincare 截面映射图 4(c)为一些散点集,说明系统响应在 $\tau = 50{\text{~}}150$ 范围内做混沌运动。而由频谱图 4(f)同样可知响应为混沌运动,表现为频谱有多种频率成分并且具有随机运动的特征,由时间历程图 4(d)得到系统平均振动幅值为 X1a = 0.500 7,最大振动幅值为 X1max = 1.263 0。
|
图 4 ω=0.8、α= 5×10-4时系统振动响应 Fig. 4 vibration responses of the system for ω=0.8 and α= 5×10-4 |
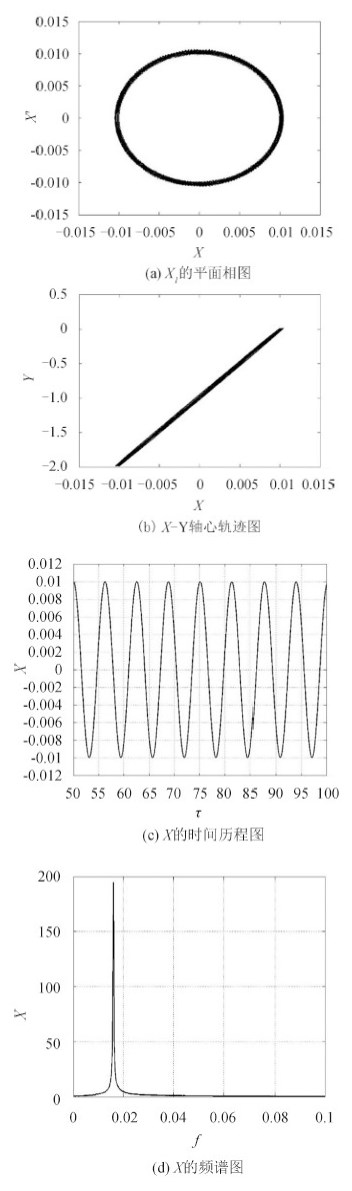
图 5 为 α = 0 时系统的振动响应特性曲线。由图 5 可知,当 α = 0 时,系统运动响应存在周期运动,表现为平面相图 5(a)为封闭的曲线和频谱图 5(d)存在唯一基频。又由时间历程图 5(c)可知,系统振动幅值|X1|在 $0 \sim 0.01$ 范围内周期变化,平均振动幅值为 X1a = 0.006 6。与图 4 中的系统响应结果比较可以看出,当轴系存在偏角不对中时,系统运动形式从简单规律的周期运动变为复杂随机的混沌运动,并且系统振动大幅度提高。
|
图 5 α = 0时系统振动响应 Fig. 5 The vibration responses of the system for α = 0 |
2)转轴质量比m'对系统振动特性的影响
分析 α = 5 × 10 -4 ,$m' = 0.1 \sim 1.0$ 时,轴系的振动特性。
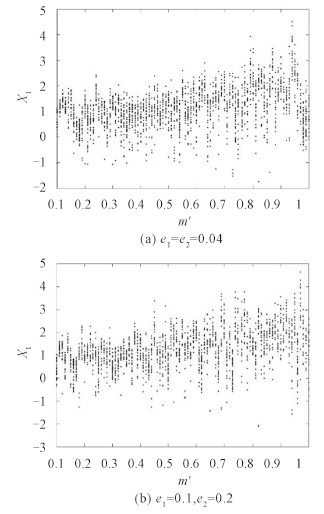
由图 6(a)和图(b)可知,当ω= 2.0时,在$m' = 0.1 \sim 1.0$ 整个范围内,轴系响应同样存在概周期运动和混沌运动,随着转轴质量比的增大振动幅值成不规则变化。
|
图 6 ω = 2,α = 5 × 10-4时,无量纲位移X1 的分岔图 Fig. 6 The bifurcation diagrams of X1 for ω = 2, α = 5 × 10-4 |
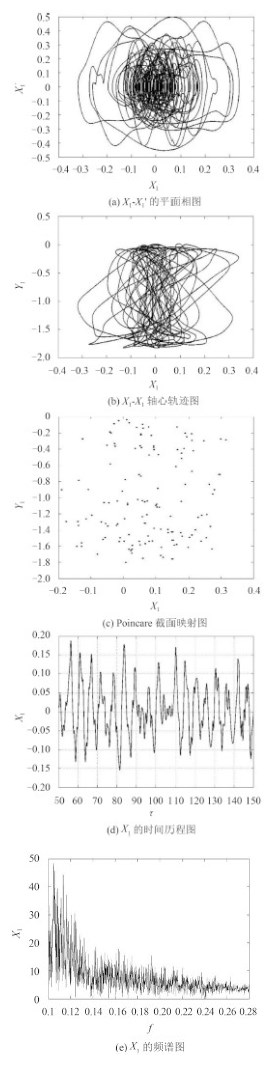
由系统响应的平面相图 7(a)和轴心轨迹图 7(b)可知,系统响应存在概周期运动和混沌运动。又根据 Poincare 截面映射图 7(c)可以清楚看出,响应为混沌运动。从时间历程图 7(d)可知,平均振动幅值为 X1a = 0.003 0 ,最大振动幅值为 X1max = 0.033 97 。比较频谱图 4(f)和图 7(f),系统振动幅值显著降低,说明当转轴偏心量 e、转轴转速ω和不对中偏角量 α 相同时,转轴质量比 m 由 0.8 降到 0.3 ,系统振动得到抑制。
|
图 7 ω=0.8, m' = 0.3时系统振动响应 Fig. 7 The vibration responses of the system for ω=0.8, m'=0.3 |
3)转轴转速 ω对系统振动特性的影响
分析 α = 5 × 10 -4 ,m = 0.8 ,ω= 0.2 ~ 2.0时,轴系的振动特性。
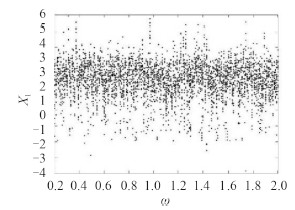
图 8 给出了 α = 5 × 10 -4 时轴系响应的分岔图。由图 8 可知,在分布范围 ω= 0.2 ~ 2.0 内,系统存在概周期运动和混沌运动,横向振动幅度较大。随着主动轴无量纲转速的增大振动幅值成无规律变化。
|
图 8 以转轴速度ω为参量的分岔图 Fig. 8 The bifurcation diagrams with rotation speed for the parameter |
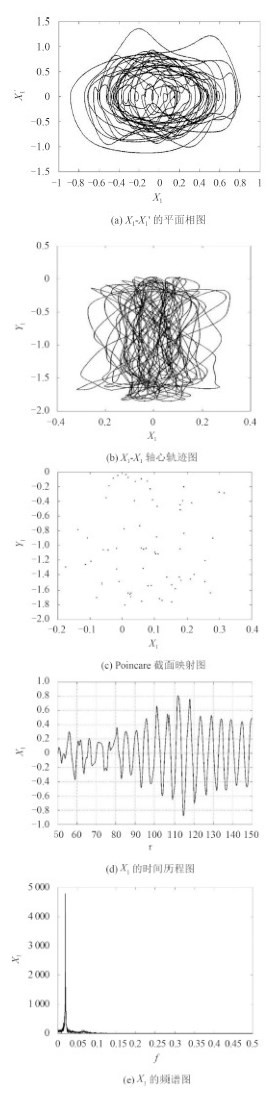
由系统振动响应特性曲线可知,系统在 τ = 50 ~ 150 范围内做混沌运动。而由时间历程图 9(d)可知,系统平均振动幅值为 X1a = 0.295 7 ,最大振动幅值为 X1max = 0.807 0 。比较频谱图 7(f)和图 9(f),系统振动幅值明显增加,说明当不对中偏角量 α、转轴质量比 m'和转轴偏心量 e 相同时,转轴转速 ω由 0.8 提高到 1.4 ,系统振动得到加强。
|
图 9 α=5×10-4, ω=1.4时轴系振动响应 Fig. 9 The vibration responses of the system for α=5×10-4, ω=1.4 |
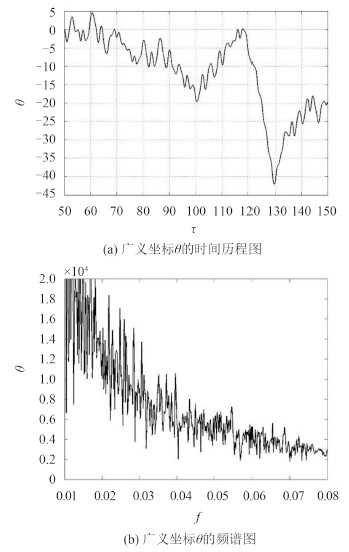
由θ的时间历程图 10(a)和频谱图 10(b)知,θ是时间的函数,表现为混沌运动,且振动幅度大,说明θ不能被视为常量或是小量,因此不能采用级数展开的近似法求解系统的解析解。
|
图 10 α=5×10-4, ω=1.4时,广义坐标θ的时间历程图和频谱图 Fig. 10 The time history chart and spectrum chart of generalized coordinates θ for α=5×10-4 and ω=1.4 |
通过计算分析偏角不对中轴系匀速过程横向振动特性,可知:
1)由于存在偏角不对中,广义坐标θ为具有复杂变化的时间函数,使偏角不对中轴系成为强非线性、非定常的三自由度耦合系统,导致难以求出系统的解析解;偏角不对中与转轴偏心量相结合改变了轴系横向振动的质量矩阵、阻尼矩阵和力矩阵,使轴系的固有频率发生变化进而影响轴系的振动特性。
2)偏斜因素导致的非线性使得系统呈现出复杂多变的振动特征,并且这些特征的变化难以从理论上进行控制,表现为:①当存在偏角不对中时,系统运动响应从简单规律的周期运动变为复杂的混沌运动,且振动幅度增大;给定转速情况下,随着不对中偏角量的变化,系统振动幅值较大且随机变化,系统响应存在概周期运动和混沌运动等复杂形式,表现为系统产生复杂的轴心轨迹图、时间历程图和功率谱图。②给定不对中偏角量情况下,随着转轴质量比和主动轴转速的变化,系统响应同样存在概周期运动和混沌运动等复杂形式,并且系统振动幅值也是随机变化。③适当减小转轴质量比或者降低转轴转速,系统振动能够得到一定抑制。④较小的转轴偏心量变化对轴系的振动响应形式影响较小。
3)由于存在偏角不对中,系统产生非线性和运动耦合,形成了复杂的非线性动力学行为,表现为概周期运动和混沌运动。初始条件的微小变化会使系统振动响应产生较大误差,导致更为复杂的运动响应变化。这种振动响应的复杂性、初态敏感性、自发随机性和长期预测的不可能性,决定了偏角不对中轴系非线性振动理论研究的难度。
4)为了避开理论研究难题,可以利用本文算列所示方法进行大量数值仿真计算,确定抑制轴系振动的偏角量阈值,从而制定最大容许的轴系不对中工艺误差以更高效地指导舰船推进轴系制造加工的工程实践。
| [1] | 李明. 平行不对中转子系统的非线性动力学行为[J]. 机械强度, 2005, 27(5):580-585. |
| [2] | 黄典贵, 蒋滋康. 交角不对中轴系的扭振特性分析[J]. 汽轮机技术, 1995, 37(3):150-152. |
| [3] |
周奇郑, 王德石, 张恺. 加速过程偏角不对中轴系横向振动特性研究[J]. 动力学与控制学报, 2014, 12(4):315-320. ZHOU Qi-zheng, WANG De-shi,ZHANG Kai.Lateral vibrationcharacteristics analysis ofshafting with angle misalignment in accelerating process[J]. Journal of Dynamics and Control, 2014, 12(4):315-320. |
| [4] | XU M, MARANGONI R D. Vibration analysis of a rotor-flexible coupling-rotor system subject to misalignment and unbalance, Part I:Theoretical model and analysis[J]. Journal of Sound and Vibration, 1994, 176(5):663-679. |
| [5] | XU M, MARANGONI R D. Vibration analysis of a rotor-flexible coupling-rotor system subject to misalignment and unbalance,Part II:experimental and validation[J]. Journal of Sound and Vibration, 1994, 176(5):681-691. |
| [6] | AL-HUSSAIN K M,REDMOND I. Dynamic response of two rotors connected by rigid mechanical coupling with parallel misalignment[J]. Journal of Sound and Vibration, 2002, 249(3):483-498. |
| [7] | AL-HUSSAIN K M. Dynamic stability of two rigid rotors connected by a flexible coupling with angular misalignment[J]. Journal of Sound and Vibration, 2003, 266(2):217-234. |
| [8] | 张宇文. 鱼雷总体设计原理与方法[M]. 西安:西北工业大学出版社, 1998 |
 2016, Vol. 38
2016, Vol. 38
