压载水管理公约 D2 规定,每立方米排放的压载水中所含的最小尺寸大于或等于 50 μm 的活性有机物少于 10 个,对压载水中颗粒物粒径范围及含量做出了明确规定[1]。水力旋流器作为一种高效可靠的机械过滤方式,能够利用水流的高速旋转运动产生的离心力将压载水中与水密度相差较大的颗粒物分离出来[2]。近年来,水力旋流器在船舶压载水处理系统中也逐步开始应用。但由于其在处理与压载水密度较近的颗粒物时,会受到一定限制。因此,本文将水力旋流器作为过滤预处理手段应用在压载水处理系统中,作用是除去密度比水大的颗粒物,如泥沙、原生动物等,从而降低压载水的浑浊度。
然而,为了提高水力旋流器的分离效率,更好地满足 IMO 标准,本文对水力旋流器的入口结构进行优化。应用 Fluent 软件,结合雷诺应力模型和多相流分析方法,对阿基米德螺线入口结构的旋流器进行固-液两相分离数值模拟,并对比分析模拟结果。
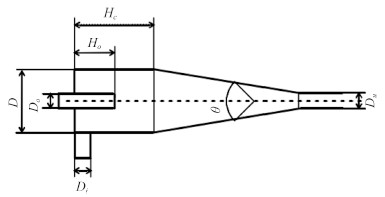
1 旋流器的优化设计水力旋流器的结构参数包括旋流器直径 D,给矿口尺寸 Di,溢流口直径 D0,底流口直径 Du,锥角 θ,溢流管插入深度 H0和柱段长度 Hc[3],其结构参数如图 1 所示。
|
图 1 水力旋流器结构参数 Fig. 1 Structural parameters of hydrocyclone |
旋流器的结构虽然简单,但其任何结构和尺寸的变化都会影响流动特性和分离性能。其中水力旋流器分离所需的离心力通过入口结构来实现。旋流器的常见入口形式为切向入口,但是其流线突然变化,沿程阻力损失较大,引起的局部能量耗损较大,从而易于产生紊流及湍流脉动等影响分离过程[4]。旋流器入口结构形式还有对数螺线形、渐开线形、同心圆形、阿基米德螺旋线形等。龚伟安用理论计算方法对比了切线形、对数螺线形、阿基米德螺旋线形入口的阻力系数,认为阿基米德螺旋线形入口的阻力系数最小[5]。此外,阿基米德螺线形入口结构,具有逐渐收缩的特性,能够增加流体转动速度,降低局部能量消耗,提高分离效率。因此,本文设计阿基米德螺线形入口的水力旋流器,为了对比2种入口形式旋流器的分离效率,2种模型均采用相同的结构尺寸,如表 1 所示。
|
|
表 1 旋流器结构尺寸 Tab.1 Structural sizes of hydrocyclone· |
旋流器内的流场是一种高雷诺数、强旋流流动,由于强旋流场中的流线呈高速旋转、弯曲,且变化迅速等特点,标准的 k-ε 模型已不能准确描述内部流场特征[6]。由于雷诺应力湍流模型增加了湍动能和湍动能耗散率并考虑到了湍流粘度的各项异性,使复杂强旋流场的模拟结果具有更高的预测精度[7]。本次模拟采用雷诺应力模型 (RSM),雷诺应力模型所对应的方程包括:
连续性方程:
| $ \frac{{\partial {U_i}}}{{\partial {x_i}}} = 0\text{,} $ | (1) |
运动方程:
| $ \begin{array}{l} \rho (\displaystyle\frac{{\partial {U_i}}}{{\partial t}} + {u_j}\frac{{\partial {U_i}}}{{\partial {x_j}}}) = - \frac{{\partial P}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}[\mu (\frac{{\partial {U_i}}}{{\partial {x_j}}} + \frac{{\partial {U_j}}}{{\partial {x_i}}}) - \\ \quad\quad\quad\quad\quad\quad\quad\quad \rho \overline {{{u'}_i}{{u'}_j}}] + \rho {g_i}\text{。} \end{array} $ | (2) |
雷诺应力运输方程:
| $ \rho \displaystyle\frac{{{\rm d}\overline {{{u'}_i}{{u'}_j}} }}{{{\rm d}t}} = \frac{\partial }{{\partial {x_i}}}(\frac{{{\mu _t}}}{{{\sigma _k}}} + \mu \frac{{\partial \overline {{{u'}_i}{{u'}_j}} }}{{\partial {x_i}}}) + {p_{ij}} - \frac{2}{3}{\delta _{it}}\rho \varepsilon + {\varPhi _{ij}}\text{,} $ | (3) |
湍动能方程:
| $ \rho \frac{\text{\rm d}k}{\text{\rm d}t}=\frac{\partial }{\partial {{x}_{l}}}[\frac{{{\mu }_{t}}}{{{\sigma }_{k}}}+\mu \frac{\partial k}{\partial {{x}_{l}}}]-\rho \overline{{{u}_{i}}{{u}_{l}}}\frac{\partial {{U}_{i}}}{\partial {{x}_{l}}}-\rho \varepsilon \text{,} $ | (4) |
湍动能耗散方程:
| $ \begin{array}{l} \rho \displaystyle\frac{{{\rm{d}}\varepsilon }}{{{\rm{d}}t}} = \frac{\partial }{{\partial \mathop x\nolimits_l }}\left[{\left( {\frac{{\mathop \mu \nolimits_t }}{{\mathop \sigma \nolimits_\varepsilon }} + \mu } \right)\frac{{\partial \varepsilon }}{{\partial \mathop x\nolimits_l }}} \right] - \\ \quad\quad\quad \mathop C\nolimits_{\varepsilon 1} \displaystyle\frac{\varepsilon }{k}\frac{{\mathop \mu \nolimits_t }}{2}\left( {\frac{{\partial \mathop u\nolimits_i }}{{\partial \mathop x\nolimits_j }} + \frac{{\partial \mathop u\nolimits_j }}{{\partial \mathop x\nolimits_i }}} \right){}^2 -\mathop C\nolimits_{\varepsilon 2\rho } \displaystyle\frac{{\mathop \varepsilon \nolimits^2 }}{k}\text{。} \end{array} $ | (5) |
其中,${\delta _{it}}$为 Kronecker 符号,k 为湍动能,ε 为湍动能耗散率;μt 为湍动粘度;${\mu _l} = \rho {C_u}\frac{\varepsilon }{k}$,Cu为湍流粘度各向异性系数;${p_{ij}} = \rho (\overline {{u_i}{u_l}} \frac{{\partial {U_j}}}{{\partial {x_l}}} + \overline {{u_j}{u_l}} \frac{{\partial {U_i}}}{{\partial {x_l}}})$。
2.2 固-液两相流模型混合模型(Mixture)是一种简化的多相流模型,适合液流中有混合、分离的情况。该模型求解混合相的动量、连续性和能量方程,各相的体积分数方程以及相间滑移速度。此外混合模型把每相当成单相流处理,忽略相互作用,采用滑移速度的概念,通过求解混合相的动量、连续性和能量方程,第2相的体积分数方程模拟 n 相(流体或粒子),并通过相对速度代数表示[8]。典型的应用包括:沉降、旋风分离器等。因此,本文的固-液两相流模型选择混合模型。
2.3 三维模型及网格划分根据旋流器的结构尺寸,分别建立切向入口结构和阿基米德螺线形入口结构的旋流器,几何模型如图 2 所示;利用 Gambit 划分结构网格,如图 3 所示。

|
图 2 几何模型 Fig. 2 The geometric model |

|
图 3 网格图 Fig. 3 Mesh diagram |
1)液相边界条件:入口边界采用速度入口,取垂直于入口端面的平均速度 ul,为 6.57 m/s;底流和溢流出口边界采用压力出口;固壁边界采用无滑移边界条件。
2)固相边界条件:入口边界采用速度入口,入口速度 us = ul;底流和溢流出口边界采用压力出口;固壁边界采用无滑移边界条件。
3)其他:设定水的密度:998.2 kg/m3,粘度:0.001 003 Pa·s;设定砂粒密度为 3 000 kg/m3,将离散相砂粒粒径分别设为 30 μm,40 μm,50 μm,60 μm,70 μm,80 μm,粘度 10 mPa·s,入口体积分数为 5%,质量流率为 8.327 kg/s。首先运用 RSM 模型对流体相做定常流动计算,待其结果收敛后,添加混合模型,完成对固-液两相流的数值模拟计算。
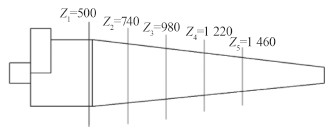
3 结果与分析为了更好地观察各截面的速度分布以及固相体积分数分布等特性,分别在柱段、锥段取 5 个截面进行分析,即 Z1 = 500 mm,Z2 = 740 mm,Z3 = 980 mm,Z4 = 1 220 mm,Z5 = 1 460 mm,截面分布图如图 4 所示。
|
图 4 旋流器轴截面简图 Fig. 4 Sketch of axial cross-sections in hydrocyclone |
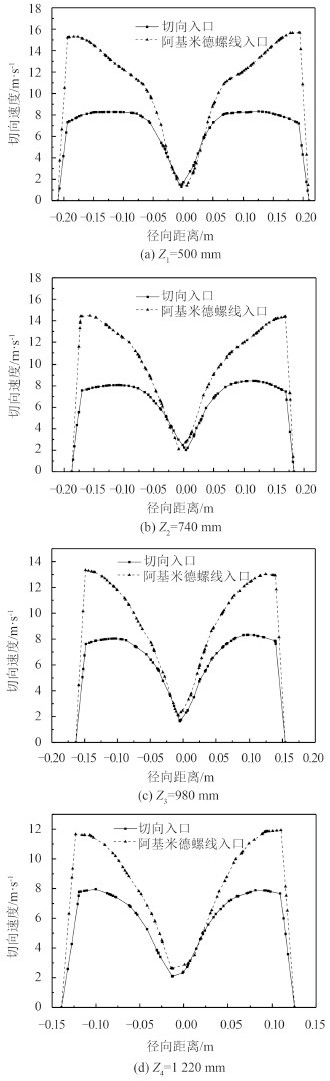
切向速度为三向速度中最重要的速度,它为旋流器的两相分离提供所需的离心力,其大小决定了旋流器的分离性能[9]。将阿基米德螺旋线入口结构和切向入口结构的2种旋流器在同一截面 Z1,Z2,Z3,Z4 上的切向速度进行对比,如图 5 所示。从图中可以看出,旋流器各截面的切向速度基本呈轴对称分布,切向速度的最小值基本都在轴心上。阿基米德螺线形入口的切向速度较切向入口均有比较大的增加,螺旋线入口在 Z1 截面上的切向速度平均值比切向入口在 Z1 截面上的切向速度平均值增加了 59.66%,Z2,Z3,Z4 截面处的切向速度平均值分别增加了 58.45%,41.73% 和 44.42%,切向速度的提高意味着离心力得到了提高,这对旋流器的分离效果有很好的促进作用。因此,从切向速度的分布上来说,阿基米德螺线形入口结构要优于切向入口结构。
|
图 5 旋流器不同截面切向速度分布图 Fig. 5 Tangential velocity distribution of different sections in hydrocyclone |
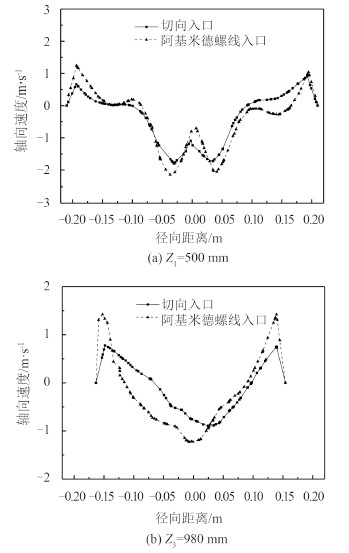
图 6(a)和图 6(b)分别为旋流器柱段和锥段内 Z1,Z3 截面上的的轴向速度分布图,轴向速度的分布构成了旋流器的外旋下行、内旋上行的双层旋转流动结构。从图中可以看出,随半径的减小,轴向速度由最大的向下流动速度逐渐减小至0,再转变为向上的速度,增大为负值。阿基米德螺旋线入口的轴向速度比切向入口的轴向速度均有较大增加,这说明向上的内涡流速度增大,使得旋流器内旋流的流动更加顺畅。此外,螺旋线入口的轴向速度在轴对称分布上要优于切向入口的轴向速度的分布,说明螺旋线入口轴向速度受到涡流的影响相对切向入口较小。
|
图 6 旋流器不同截面轴向速度分布图 Fig. 6 Axial velocity distribution of different sections in hydrocyclone |
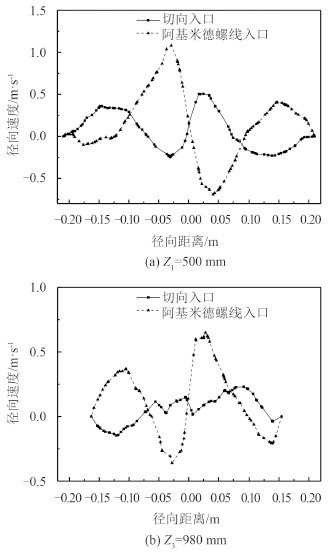
在旋流器内流体运动中,与其他两向速度相比,径向运动的速度较小。图 7(a)和图 7(b)分别为旋流器柱段和锥段内 Z1,Z3 截面上的的径向速度分布图。其中,速度为正表示向远离轴线的方向运动,为负则表示向靠近轴线方向运动。从图中可以看出,柱段内流体的径向速度波动较大,从器壁到溢流口附近,速度为正,说明流体向器壁运动,有利于固体颗粒进入外旋流;从溢流口附近至中心处,径向速度正负转换,说明此处形成循环流。流体进入锥段后,径向速度的波动减小,说明此处流体的运动已比较稳定。总的来说,阿基米德螺线入口结构比切向入口结构的径向速度分布更加均匀,数值较大,有着更稳定的流场,更有利于固相颗粒的分离。
|
图 7 旋流器不同截面径向速度分布图 Fig. 7 Radial velocity distribution of different sections in hydrocyclone |
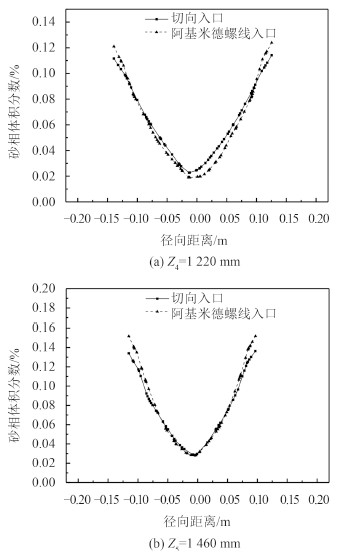
图 8 为水力旋流器内砂相体积分数分布云图,图 9 为锥段 Z4,Z5 截面上的砂相体积分布。从图 8 可以看出,当固液混合流体由入口进入旋流器后,砂相在离心力作用下实现分离,分离后砂相主要集聚在外壁,靠近壁面区域固相体积分数较高,靠近轴线区域颗粒的体积分数较低,此分布说明该水力旋流器能够实现固液的有效分离。此外,固相颗粒主要集中在锥段部分,可以认为水力旋流器的两相分离主要在锥段完成。从图 8和图 9 中可以看出,阿基米德螺线入口结构的旋流器锥段的固相体积分数要明显高于切向入口结构的旋流器,这说明阿基米德螺线入口结构有更好的分离效果。

|
图 8 砂相体积分数分布云图 Fig. 8 Distribution contours of sand fraction |
|
图 9 旋流器不同截面砂相体积分布图 Fig. 9 Sand fraction distribution of different sections in hydrocyclone |
对于旋流器来说,分离效率是评价其工作性能的一个重要指标,将分离效率定义为底流口砂相的去除百分率,因此,对于某直径砂粒的分离效率可按下式计算[10]:
| $ E = \frac{{{M_u}}}{{{M_i}}} \times 100\% \text{。} $ | (6) |
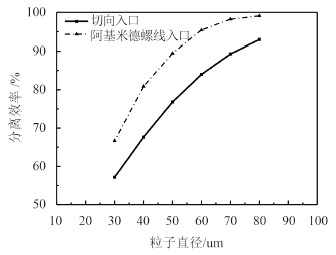
|
图 10 不同直径砂粒的分离效率 Fig. 10 Separation efficiency of the sand in different diameters |
从图中可以看出,在相同模拟条件下,砂粒直径径越大,水力旋流器的分离效率越高。与切向入口结构的旋流器相比,阿基米德螺旋线入口旋流器对不同直径砂粒的分离效率均有所增加,分别增加了 9.5%,13.26%,12.67%,11.43%,8.93% 和 6.14%;。当粒径大于 50 μm 时,阿基米德螺旋线入口旋流器的分离效率均达到了 95% 以上,其中对直径为 50 μm,60 μm,70 μm,80 μm 砂粒的分离效率分别为 89.47%,95.42%,98.23% 和 99.08%。因此,从分离效率方面来说,阿基米德螺线形入口结构要优于切向入口结构。
4 结语为了更好地满足 IMO 标准,本文对压载水预处理单元水力旋流器的入口结构进行了优化。将旋流器入口结构优化为阿基米德螺线形入口,应用 Fluent 软件,结合雷诺应力模型和多相流分析方法,分别对切向入口和阿基米德螺线入口结构旋流器的固-液两相分离进行了数值模拟,并对比分析了流场的速度分布和颗粒分布规律。模拟结果表明:
1)将旋流器入口结构优化为阿基米德螺线形后,其各截面的切向速度、轴向速度和径向速度均有所增加,其中切向速度增加的幅度较大,对提高对旋流器的分离效果起到促进作用。
2)与切向入口结构的旋流器相比,阿基米德螺旋线入口旋流器对不同直径砂粒的分离效率均有所增加。当粒径大于 5 0 μm 时,阿基米德螺旋线入口旋流器的分离效率均达到了 95% 以上,其中对直径为 50μm,60 μm,70 μm,80 μm 砂粒的分离效率分别为 89.47%,95.42%,98.23% 和 99.08%。
综上所述,将旋流器入口结构优化为阿基米德螺线形后,其切向速度增大,离心力增加,分离效率提高,达到了优化目的。在后续工作中,将着重于文中优化装置的实验研究,增加装置的有效性和实用性。
| [1] |
王军, 应胜, 陈宁. 基于压载水的除沙旋流器设计及实验研究[J]. 江苏科技大学学报(自然科学版), 2014, 28(6):552-556. WANG Jun, YING Sheng, CHEN Ning. Design and experimental study of hydrocyclone for removing sand from ballast water[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2014, 28(6):552-556. |
| [2] |
王文成, 龚帆, 郑羽, 等. 船舶压载水处理综述[J]. 上海船舶运输科学研究所学报, 2013, 36(4):11-14. WANG Wen-cheng, GONG Fan, ZHENG Yu, et al. A review of ship ballast water treatment[J]. Journal of Shanghai Ship and Shipping Research Institute, 2013, 36(4):11-14. |
| [3] |
闫月娟. 井下旋流除砂器内固液两相流动特性研究[D]. 大庆:东北石油大学, 2014. YAN Yue-juan. Research on solid-liquid flow character in downhole hydrocyclone desander[D]. Daqing:Northeast Petroleum University, 2014. |
| [4] |
曹雨平, 姜临田. 水力旋流器的研究现状和发展趋势[J]. 工业水处理, 2015, 35(2):11-14. CAO Yu-ping, JIANG Lin-tian. Research status and development trend on hydrocyclone[J]. Industrial Water Treatment, 2015, 35(2):11-14. |
| [5] | 龚伟安. 水力旋流器的蜗壳设计理论与计算[J]. 石油机械, 1992, 20(12):1-6. |
| [6] | ZHANG J, YOU X Y, NIU Z G. Numerical simulation of solid-liquid flow in hydrocyclone[J]. Chemical and Biochemical Engineering Quarterly, 2011, 25(1):37-41. |
| [7] |
应锐, 王卫兵, 邱艳军, 等. 电石渣提纯用水力旋流器的设计及优化[J]. 矿山机械, 2015, 43(4):95-98. YING Rui, WANG Wei-bing, QIU Yan-jun, et al. Design and optimization of hydrocyclone for purification of carbide slag[J]. Mining & Processing Equipment, 2015, 43(4):95-98. |
| [8] |
蔡圃, 王博. 水力旋流器内非牛顿流体多相流场的数值模拟[J]. 化工学报, 2012, 63(11):3460-3469. CAI Pu, WANG Bo. Numerical simulation of multiphase flow field of non-newtonian fluid in hydrocyclone[J]. CIESC Journal, 2012, 63(11):3460-3469. |
| [9] | 冯蕾. 烟气脱硫系统中固-液分离旋流器的三维数值研究[D]. 保定:华北电力大学, 2011. FENG Lei. The 3D numerical simulation study on solid-liquid hydrocyclone in flue gas desulfurization system[D]. Baoding:North China Electric Power University, 2011. |
| [10] |
罗力. 水力旋流器固-液两相流动数值计算及性能分析[D]. 广州:华南理工大学, 2012. LUO Li. CFD and performance prediction of a solid-liquid hydrocyclone[D]. Guangzhou:South China of Technology, 2012. |
 2016, Vol. 38
2016, Vol. 38
