在船舶航行过程中,不可避免地在尾部形成不均匀伴流场,螺旋桨在伴流场中会产生脉动激振力,该纵向力经推力轴承传递到船体,引起船体产生振动,降低船舶的舒适性和声学性能。近年来,国内外学者针对螺旋桨纵向激励通过轴系传递引起的船体振动声辐射开展了大量研究。
Goodwin[1]提出基于液力吸振原理的推进轴系的纵向振动控制技术研究,Dylejko[2]与Merz[3]等在此基础上进行深化,建立声辐射计算模型并提出半主动控制等优化方法。刘义军等[4]开展了碟簧式推力轴承理论与试验研究,取得了较好的减振效果。沈建平等[5]研究了采用舱壁式推力轴承减小轴系纵向振动。张金国等[6]提出应用法兰盘式推力轴承降低纵向激励向艇体的传递。杨志荣等[7]提出一种应用集成橡胶隔振元件的推力轴承隔离螺旋桨脉动的措施。曹贻鹏等[8]开展了基于动力吸振器的潜艇推进轴系轴向减振技术研究。
上述研究在轴系纵向振动控制措施方面取得较大成果,但在大刚度、低动静比推力轴承减振技术方面研究不足。为此,本文结合船舶推进轴系特点,研究集成液压减振技术的推力轴承。通过理论与试验分析液压减振结构的动、静态特性,提出液压减振推力轴承设计方法,并通过试验进行验证。
1 桨-轴系统纵向振动特性分析船舶推力轴承将动力装置的输出功率传递螺旋桨,并将螺旋桨产生的动力传递给船体,推动船舶航行。工作中,推力轴承不仅是船舶航行动力传递枢纽,同时也是螺旋桨纵向激励向艇体传递的主要路径。
为了降低螺旋桨纵向激励向艇体的传递,在轴系上应用隔振器是最有效的方式之一,如在轴上加装纵向减振器或减振推力轴承等。其中在推力轴承内部非旋转部件中集成纵向隔振结构是最合理的方式,因为集成后不仅可实现隔振,还可避免增加回旋振动。
由于推力轴承需传递大推力,轴系纵向位移又有严格要求,因此减振元件需要较高的静刚度。但从隔振原理分析,又要求减振元件的动刚度尽量低,以提高隔振效果。目前常用的橡胶、圆柱形弹簧、气囊等弹性减振元件的动、静刚度都难于同时满足上述要求。碟形弹簧具有轴向尺寸小、承载能力大、加压均匀和缓冲及减振能力强的特点。可通过不同的组合(叠合或对合)得到不同刚度特性,可实现在小变形条件下承受大范围变化的载荷。但是,碟簧减振器动刚度不仅与碟簧自身结构参数相关,还与静载荷、粘性阻尼、碟簧片之间摩擦形成的库仑阻尼力密切相关,动刚度非线性特性比较明显。考虑到阻尼特性自身极其复杂,难于建立准确的映射关系,而且试验表明其动、静比也较高。因此,有必要开展其他减振元件设计,获得动态特性更合理的设计方案。
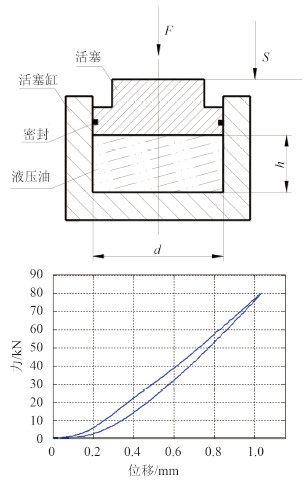
2 液压减振技术分析 2.1 液压减振模型液力减振的基本原理利用流体“可压缩性”调节系统刚度特性。如图 1 所示的活塞-活塞缸式液压减振器,活塞直径为 d(面积为 A),液压油深度为 h,液压油的体积弹性模量为 B。液压减振器的静刚度可根据外部作用力 F 及其引起的活塞位移 S 计算得到。
|
图 1 静刚度测试及其结果 Fig. 1 Test model and result of static stiff |
根据体积弹性模量 B 的定义:
| $ B = \frac{{{\rm{d}}p}}{{{\rm{d}}V/V}} = \frac{{{\rm{d}}F/A}}{{A \times {\rm{d}}S/A \times h}} \text{,} $ | (1) |
| $ S = \frac{{Fh}}{{AB}} \text{;} $ | (2) |
进而可得到静刚度 Ks 计算公式:
| $ {K_s} = \frac{F}{S} = \frac{{AB}}{h} \text{。} $ | (3) |
其中体积弹性模量的主要影响因素有包括油液中混入的空气量、结构刚度、液压油温度、液压油压力等[9]。其中含气量是最主要的影响因素,油温和油压变化所带来的影响很大程度上通过改变含气量而产生,当结构刚度足够强时可忽略因结构变形引起的刚度变化,可得出体积弹性模量的准确计算方法,具体如下:
| $ B = \frac{1}{\begin{array}{l} - 10{\delta _0}{\beta _1}M{\alpha ^2} + (10{\delta _0}M{\beta _1} + \ \displaystyle\frac{1}{{p - {p_0}}}(1 - M){\beta _1} - 1)\alpha + 1 \end{array}}{B_l} \text{,} $ | (4) |
| $ M = {\left( {\frac{{{p_0}T}}{{p{T_0}}}} \right)^{t/\gamma }} \text{。} $ | (5) |
其中,p0,T0,γ 分别为假设初始状态大气压力下、初始温度与气体绝热指数;βl 为纯液压油的体积弹性模量;α 为油液的含气量。为此液压减振器的静刚度可表述为:
| $ K = f(p,\alpha \text{,}t) \text{。} $ | (6) |
综上分析可知,理论上液压减振器的静刚度是与压力、温度、气态绝热系数密切相关的非线性函数。在工程应用中,体积弹性模量通常取值(0.9~1.4)× 10 9 Pa。以 d = 100 mm、h = 80 mm的减振器模型开展静刚度试验,试验中采用专用真空装置进行抽气,测试结果如图 2 所示。
|
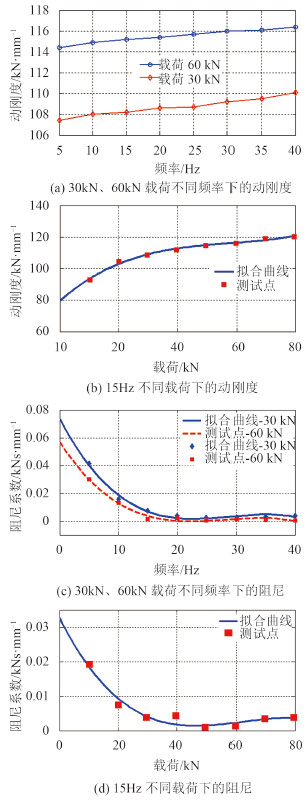
图 2 动刚度与阻尼测试结果 Fig. 2 Test result of dynamic stiff and damping |
从测试数据可知,液压减振器的静刚度约 91 kN/mm。取弹性模量 1.0 × 10 9 Pa 进行计算,计算值为 98 kN/mm,对比分析可知,计算值与测试值接近,说明前面的静刚度计算方法可行。同时,通过图 2 的静刚度曲线可知,在大于 0.2 mm 之后的行程内,静刚度线性很强,与压力没有明显的关系,因此在液压减振器静力学分析中,可采用某一合理的体积弹性模量值,可不考虑压力等因素。通过对比液压减振器的结构尺寸(直径 100 mm)与静刚度,说明液压减振器的静刚度较大,并且可通过结构设计获得优化方案。
2.2 液压减振动态特性在振动控制中,动刚度是表征动力学特性更准确的参数。相对于静刚度,动刚度影响因素更多、更复杂。以图 1 实例为模型,建立动力学方程如下:
| $ M\mathop x\limits^{ \bullet \bullet } + {C_1}\mathop x\limits^ \bullet + {F_{c2}} + {K_1}x + {F_{k2}} = F \text{,} $ | (7) |
| $ \begin{array}{l} M\mathop x\limits^{ \bullet \bullet } + C\mathop x\limits^ \bullet + {F_{c2}} + \zeta \frac{A}{h} \cdot \\ {\left[{ - 10{\delta _0}{\beta _1}M{\alpha ^2} \!+\! (10{\delta _0}M{\beta _1} \!+\! \frac{1}{{p - {p_0}}}(1 - M){\beta _1} - 1)\alpha + 1} \right]^{ - 1}}\times \\ {B_l}x + {F_{k2}} = F \text{。} \end{array} $ | (8) |
由振动微分方程可知,液压减振器动刚度不仅与自身结构参数相关,还与静载荷、粘性阻尼、活塞与活塞缸之间摩擦形成的库仑阻尼力、摩擦力密切相关,动刚度非线性特性比较明显,无法准确通过计算获得,为此在专用试验机上进行试验测试,结果如图 2 所示。
从图 3 的动刚度、阻尼曲线可知,在外部结构参数确定的动刚度、阻尼与载荷、频率具有密切关系,可归纳如下:对于同一载荷下的扫频试验,动刚度随频率的增加呈增加的趋势,但总体上比较稳定。而阻尼随频率增加而降低,最后趋于稳定;对于同一频率下的扫载荷试验,动刚度随载荷的增加而增加,趋势也是越来越平缓。而阻尼随频率增加而降低,最后也趋于稳定。从试验结果分析,动刚度、阻尼具有较强的非线性,难以直接从理论上建立计算公式,需通过试验测试数据进行拟合。
|
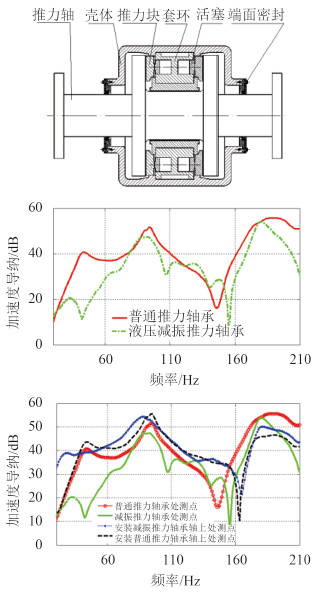
图 3 液压减振推力轴承及其试验插入损失、振级落差 Fig. 3 Structure and test result of hydraulic thrust bearing |
由结果可知 20 Hz 时 30 kN 与 60 kN 的动刚度分别为 108 kN/mm 与 116 kN/mm,而静刚度为 91 kN/mm,因此可分别计算出2种状态下的动静比分别为 1.18 与 1.27。与碟簧、橡胶减振器的动静比 1.6 相比,在设计中具有明显优势。从前面的分析也可看出,可将动静比 ζ 简化为一常数进行初步设计,最终通过试验进行验证并修正。
3 液压减振推力轴承设计及试验推力轴承一般由推力轴、推力块、推力平衡传递机构、壳体、支撑轴承和管路附件等组成。推力通常通过以下路径传递:推力轴→推力块→推力平衡传递机构→壳体→基座→艇体。液压减振推力轴承是在推力传递路径之间,即推力轴至推力轴承壳体之间设置减振元件,调节推力轴承纵向刚度,达到纵向减振目的。
根据螺旋桨纵向激励特性,为了达到纵向减振目的,推力轴承纵向刚度需小于 200 kN/mm,为此在推力轴承内部设置 8 个液压减振器,每个液压减振器的刚度不大于 25 kN/mm。结合推力轴承自身结构,最终确定活塞缸直径 50 mm,深度 105 mm,参考前面液压减振器动、静刚度计算方法,8 个液压减振器的系统静刚度为 142.4 kN/mm。由于布置 8 个活塞孔的套环模型尺寸超过动刚度试验机平台,无法专用试验机上进行测试。为此在试验平台中通过加载力、测试变形的方法获得静刚度约 134.4 kN/mm。初步设计中取动静比 1.3,估算系统动刚度为 194 kN/mm。
为了进一步分析碟簧减振推力轴承的振动传递特性,在试验台架对推力轴承进行振动试验。试验台包括推进电机、弹性联轴器、中间轴承、中间轴、推力轴承、推力加载装置等。通过推力加载装置对推力轴承施加静态力,在推力轴尾端法兰进行锤击,在推力轴尾端与推力轴承壳体上布置测点,测量振动加速度,分析振级落差。试验台架各主要部分的参数见表 1。
|
|
表 1 主要参数 Tab.1 Design parameter of test platform |
为了更有效地验证减振效果,同时进行无液压减振功能的推力轴承试验,对比分析液压减振器的插入损失与振级落差,结果如图 3 所示。
从测试结果可知,安装液压减振推力轴承前后系统一阶固有频率分别为 25.2 Hz 与 38.5 Hz。根据系统刚度与质量计算值分别为 26.4 Hz与 40.4 Hz,测试与计算值接近,前面动刚度估算值 194 kN/mm 准确可行。同时由测试结果可知,集成液压减振器后的推力轴承明显降低了轴系纵向激励向艇体的传递,对推进系统纵向振动控制提供了有效途径。
4 结语分析船舶推进系统纵向减振特点,总结现有减振元件静、动态特性并提出液压减振器模型,研究液压减振器动力学模型并通过试验进行验证,最后对集成液压减振器的推力轴承进行理论计算与试验分析,通过研究可得出以下结论:
1)液压减振器静刚度线性特性较好,理论计算与试验测试值吻合。
2)液压减振器动态特性复杂,不仅与结构参数相关,还与外部静载荷、频率等密切相关,准确值难以直接通过理论计算获得。但考虑动静比较小,可通过静刚度与动静比值进行估算。
3)液压减振推力轴承在减少尾部纵向激励向艇体传递方面具有明显效果,可为船舶轴系减振降噪设计提供技术基础。
| [1] | GOODWIN A J H. The design of a resonance changer to overcome excessive axial vibration of propeller shafting[J]. Institute of Marine Engineers Transactions, 1960, 72:37-63. |
| [2] | DYLEJKO P G, KESSISSOGLOU N J, TSO Y, et al. Optimisation of a resonance changer to minimise the vibration transmission in marine vessels[J]. Journal of Sound and Vibration, 2007, 300(1/2):101-116. |
| [3] | MERZ S, KESSISSOGLOU N, KINNS R, et al. Minimisation of the sound power radiated by a submarine through optimisation of its resonance changer[J]. Journal of Sound and Vibration, 2010, 329(8):980-993. |
| [4] | 刘义军, 刘伟, 俞强. 碟簧式减振推力轴承纵向振动特性研究[C]//2014年第11届全国转子动力学学术研讨会论文集. 大连:中国振动工程学会, 2014. |
| [5] | 沈建平, 周文建, 童宗鹏. 船舶传动装置振动控制技术研究现状与发展趋势[J]. 舰船科学技术, 2010, 32(8):7-12. |
| [6] | 张金国, 姚世卫, 王隽. 法兰盘式推力轴承推进轴系振动传递特性分析研究[J]. 噪声与振动控制, 2008(2):23-25, 36. |
| [7] | 杨志荣, 秦春云, 饶柱石, 等. 船舶推力轴承纵向橡胶减振器设计[J]. 噪声与振动控制, 2013, 33(6):211-215. |
| [8] | 曹贻鹏. 推进轴系引起的艇体结构振动与辐射噪声控制研究[D]. 哈尔滨:哈尔滨工程大学, 2008. |
| [9] | 冯斌. 液压油有效体积弹性模量及测量装置研究[D]. 杭州:浙江大学, 2011. |
 2016, Vol. 38
2016, Vol. 38
