2. 中国船舶及海洋工程设计研究院, 上海 200011;
3. 喷水推进重点实验室, 上海 200011
2. Marine Design and Research Institute of China, Shanghai 200011, China;
3. Key Laboratory of Waterjet Propulsion, Shanghai 200011, China
喷水推进是一种广泛应用于中高速船舶、具有时代特征的先进推进方式,由以喷水推进器为核心的喷水推进装置实现推进与操纵的双重功能。喷水推进器[1]由进口流道、推进泵、喷口组成,进口流道水动力性能对整个推进系统的推进效率有很大影响[2]。进口流道设计的优劣不仅会直接影响流道的能量损失,也会对下游进入推进泵水流的均匀度与能量有明显作用,会影响推进泵流场的稳定性和抗空泡性能。而描述进口流道的参数很多,且各参数之间相互联系,改变其中一个参数其他参数也会相应的发生改变,这使得进口流道效率的研究很复杂,也是进口流道设计的难点。因此必须对进口流道各参数之间的关系以及进口流道倾斜角对效率的影响做研究,这将对工程设计有很好的指导意义。
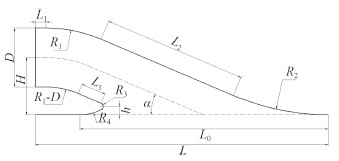
1 进口流道倾斜角与其他特征参数之间的关系描述喷水推进进口流道的主要参数如图 1 所示,共有 13 个。流道倾斜角 α 为进口流道轴线与船底板夹角。流道总长 L、流道高度 H、流道特征直径 D 与装置规格和布置安装有关,在设计进口流道之前已经确定,设计时,这 3 个值保持不变。
|
图 1 进口流道特征尺寸示意图 Fig. 1 The feature dimensions of inlet duct |
图 1 中:L1为水平直管段长度;R1为背部圆弧弯管段半径;L2为背部倾斜直管段长度;R2为背部与船底倒圆半径;R1 - D为下侧圆弧弯管段半径。L3为下侧倾斜直管段长度;R3为唇口上部倒圆半径;h为唇口上部倒圆圆心与船底垂直距离;R4为唇口下部倒圆半径;L0为流道进口长度;
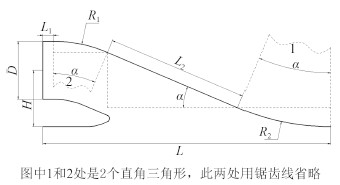
如图 2 所示(图中虚线为辅助线),背部线型在水平方向上满足
| $ {L_1} + {R_1} \cdot \sin \alpha + {L_2} \cdot \sin \alpha + {R_2} \cdot \sin \alpha = L \text{,} $ | (1) |
|
图 2 进口流道背部尺寸示意图 Fig. 2 The back dimensions of inlet duct |
在竖直方向上满足,
| $ {R_{1}}\cdot \left( 1-\cos \alpha \right)+{L_{2}}\cdot \sin \alpha + {R_{2}}\cdot \left( 1-\cos \alpha \right)\ =H+\frac{D}{2} \text{,} $ | (2) |
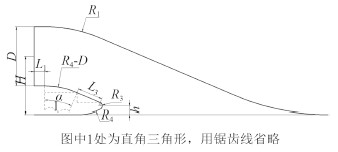
对于唇口部分如图 3 所示,同样在竖直方向上满足,
| $ \left( {R_{1}}\!-\!D \right)\cdot \left( 1\!-\!\cos \alpha \right)\!+\!{L_{3}}\cdot \sin \alpha \! +\! {R_{3}}\cdot \cos {\alpha{α}} +h\ =H-\!\frac{D}{2}\text{,} $ | (3) |
|
图 3 唇口尺寸示意图 Fig. 3 The lip dimensions of inlet duct |
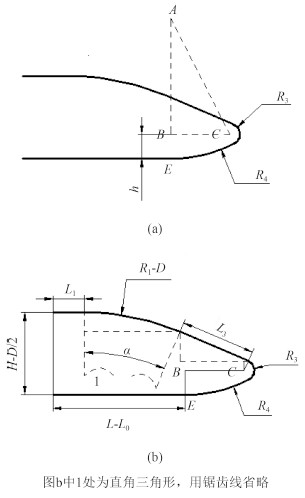
在图 4(a)中,点 E 为圆弧 R4 与船底切点,点 B 在点 E 竖直上方 h 处,A 为圆弧 R4 圆心,C 为圆弧 R3 圆心。在直角三角形 ABC 中满足勾股定理,
| $ {{AB}^{2}}+{{BC}^{2}}={{AC}^{2}} \text{,} $ | (4) |
|
图 4 唇口局部示意图 Fig. 4 The local dimensions of lip |
从图 4(a)中可得出:
| $ AC={{R}_{4}}-{{R}_{3}}\text{,} $ | (5) |
| $ AB={{R}_{4}}-h\text{;} $ | (6) |
在图 4(b)中有
| $ \begin{array}{l} BC = {L_3}\cos \alpha + ({R_1} - D - {R_3}){\rm{sin}}\alpha - \ (L - L{}_0 - {L_1})\text{。} \end{array} $ | (7) |
| $ \begin{array}{l} {({R_4} - h)^2} + ({L_3} \cdot \cos \alpha + ({R_1} - D - {R_3}){\rm{\cdot}}{\rm{sin}}\alpha - \ (L - {L_0} - {L_1}){)^2} = {({R_4} - {R_4})^2}\text{。} \end{array} $ | (8) |
式(1)、式(2)、式(3)、式(8)是 4 个独立的方程,共包含 13 个参数,其中流道特征直径 D、流道高度 H、流道总长度 L 这 3 个参数与船体总布置有关,当倾斜角 α 发生变化时,这3个参数保持不变,其余 9 个参数随倾斜角变化。在研究流道倾斜角 α 对流道效率的影响时,理想的情况是只改变倾斜角 α,而剩下的其他 9 个参数都保持不变,但由以上推导的 4 个独立方程可知,当流道倾斜角 α 改变时,必须从剩下的 9 个参数中选取 4 个参数随流道倾斜角 α 发生变化,其他 5 个参数保持不变。在这剩下的 9 个参数中 L1,L2,L3 的改变对进口流道效率的影响较小,当流道倾斜角 α 改变时让这 3 个参数随之改变,那么还要在剩下的 6 个参数中选取第 4 个参数随倾斜角 α 变化,这 6 个参数分别为 R1,R2,R3,R4,L0,h。
当第4个参数取 R1 时,R2,R3,R4,L0,h 全都保持不变。将式(3)减去式(2)可以得到,
| $ \begin{aligned} {L_3} \! - \! {L_2} \! = \! - \frac{1}{{{\rm{sin}}\alpha }}D \! +\! {h + }{R_3}{\rm{cos}}\alpha \! - \! ({R_2} + D) (1 \! - \! {\rm{cos}}\alpha ) \text{,} \end{aligned} $ | (9) |
将式(1)和式(9)式代入式(8)可得:
| $ \begin{aligned} ( - \frac{{{\rm{cos}}\alpha }}{{{\rm{sin}}\alpha }}(D & + {H + }{R_3} \cdot {\rm{cos}}\alpha - ({R_2} + D)(1 - {\rm{cos}}\alpha )-\\ & (D + {R_3}){\rm{sin}}\alpha - {R_2} \cdot {\rm{sin}}\alpha + {L_0}{)^2}=\\ & {({R_4} - {R_3})^2} - {({R_4} - h)^2} \text{。} \end{aligned} $ | (10) |
从式(10)可以看出,如果第 4 个参数选 R1,D,R2,R3,R4,L0,h 都保持不变,则等式右边的值也保持不变,当等式左侧流道倾斜角 α 取不同的值时,等式左边的值也会发生变化,显然等式将不能成立,因此第 4 个参数不能取 R1,第 4 个参数将只能取R2,R3,R4,L0,h 这 5 个中的 1 个。
2 进口流道效率衡量准则定义进口流道的效率为[3],
| $ \eta = \frac{{{{\rm{E}}_{{\rm{in}}}}}}{{{{\rm{E}}_{{\rm{out}}}}}} \times 100\% \text{,} $ | (11) |
| $ E = \int {[\frac{1}{2}\rho {u^2} + (p - {p_0}) - \rho gx]} {\rm{d}}Q \text{。} $ | (12) |
式中:ρ 为流体密度,kg/m3;u 为截面速度,m/s;p 为截面压强,pa;p0 为大气压力,pa;g 为重力加速度,m/s2;x 为距离势能参考面高度,m。
虚拟进口流道截面的形状和位置没有统一的规定,第 24 届 ITTC 喷水推进专家委员会会议[4]建议虚拟进口流面的形状为椭圆,即用椭圆拟合虚拟面的形状,在拟合时为了保证质量守恒,虚拟椭圆面的流量必须与出口截面的流量相等。虚拟进口截面如果离实际进口太近会受到流动变形的影响,而如果距离实际进口太远,又会使效率计算不准确,研究发现把虚拟进口流面的位置取在距离进口 1 D 的距离较好,本文也将虚拟流道截面位置取在距离实际进口 1 D 的位置。
3 实例计算为研究流道倾斜角 α 发生变化时进口流道效率的变化规律,以中国船舶及海洋工程设计研究院某型喷水推进装置进口流道为基础,保持特征直径 D、流道高度 H、流道总长度 L 不变,以流道倾斜角 α 为变量,该角依次取 22°,23°,24°,25°,26°,27°。根据 1 节的分析结果,当流道倾斜角 α 发生改变时,随之改变的 4 个参数可以分别取为以下 5 组:
1)L1,L2,L3,R3; 2)L1,L2,L3,R2;
3)L1,L2,L3,R4; 4)L1,L2,L3,h;
5)L1,L2,L3,L0。
当选第 1 组 4 个参数随流道倾斜角 α 改变时,经计算,在倾斜角为 24°,25°,26°,27°时相应的 R3 为复数,无物理意义。所以第 4 个参数依次取为 R2,R4,h,L0。表 1~表 4 为第 4 个参数分别选 R2,R4,h,L0 时进口流道的参数。
|
|
表 1 第 4 个参数为 R2 时进口流道参数 Tab.1 The dimensions of inlet duct when the fourth parameter is R2 |
|
|
表 2 第 4 个参数为 R4 时进口流道参数 Tab.2 The dimensions of inlet duct when the fourth parameter is R4 |
|
|
表 3 第 4 个参数为 h 时进口流道参数 Tab.3 The dimensions of inlet duct when the fourth parameter is h |
|
|
表 4 第 4 个参数为 L0 时进口流道参数 Tab.4 The dimensions of inlet duct when the fourth parameter is L0 |
当流道倾斜角变化时,4 个变量分别取第 2 ~ 5 组中的 4 个参数。除每组的 4 个参数和流道倾斜角 α 发生变化外,其他 8 个参数保持不变。然后在三维建模软件 Pro/E 中建立进口流道三维模型。
3.1 网格划分在进口流道建模时,计算流域范围的长、宽、深分别取 30 D,10 D,8 D,其中 D 为进口流道特征直径。
在划分网格时,要反映唇口的实际形状很困难,如果采用结构网格和 O 型网格拓扑虽然可以提高网格的质量,但是在某些区域网格扭曲比较严重,会影响计算精度,因此决定采用非结构网格。非结构网格的缺点是不能很好的反应边界层的流动,为解决这问题,可以在有边界层的区域划分三棱柱网格[5],即在划分网格时采用四面体和三棱柱混合的非结构网格,其中[6]y+ 取 60。
3.2 湍流模型计算时采用 RNG κ - ε 湍流模型[7]。与 Standard κ - ε 湍流模型相比,RNG κ - ε 湍流模型修正了湍流粘度,考虑了流动中的旋转,更适合计算弯曲程度较大的流动[8]。进口流道中的流体的流动弯曲比较大,采用该种湍流模型较合适。
3.3 边界条件在进流处将边界条件设为速度入口,且速度为船速;上出口设为流量出口;下出口设为压力出口;船底和流道设为固壁;为进一步增加流域范围,流域的底面和 2 个侧面边界条件设为对称边界。

|
图 5 进口流道三维模型及流域 Fig. 5 The 3D model and flow field of inlet duct |

|
图 6 进口流道网格 Fig. 6 The mesh of inlet duct |
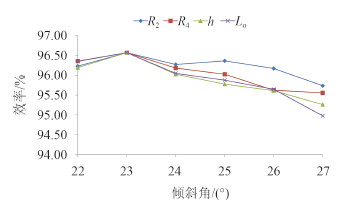
通过在 Fluent 中求解,将进口流道的效率绘制成图,如图 7 所示,其中图例“R2”表示“第 4 个参数取 R2”,图例 R4,h,L0 意义同上。
|
图 7 不同流道倾斜角下流道效率 Fig. 7 The efficiency of inlet duct at different titling angle |
从图 7 的计算结果可以看出,第 4 个参数为 R2 时,当倾斜角从 23° ~ 26°变化时,流道效率基本没有差别,26°以后效率加速下降;第 4 个参数为 R4 时,在倾斜角为 23° ~ 26°区间内,效率下降较快,26°以后趋于平稳;第 4 个参数为 h 时,在倾斜角为 23° ~ 26°区间,效率一直降低;第 4 个参数为 L0 时,在倾斜角为 23° ~ 26°区间效率下降较慢,26°以后效率下降加快。但是无论第 4 个参数选哪一个,不同流道倾斜角下,流道效率相差不超过 2%,且流道效率都在 23°时达到最大。
4 结语本文推导并建立喷水推进进口流道各特征参数之间的内在联系,随后以某型喷水推进器进口流道和工作参数为基础,以流道倾斜角为变量,应用参数之间的关系,建立多组模型,用CFD技术模拟进口流道流场,并计算流道效率,得出如下结论:
1)第 4 个参数选为 R2 时,流道效率随流道倾斜角的下降最小。
2)当流道倾斜角从 22° ~ 27°之间改变时,第4个参数选取不同,进口流道效率变化规律也不同,但流道效率都在23°时达到最大,当流道倾斜角从23°~27°变化时,流道效率整体上都会随着倾斜角的增加而减小。
3)流道倾斜角从22°~27°改变时,无论第4个参数选哪一个,各倾斜角对应的流道效率最大差别不超过2%,所以在实际的设计中,如果流道倾斜角不能取的太小,可以适当增加倾斜角而不会对流道效率有太大影响,有利于控制装置长度与重量。
| [1] |
金平仲. 船舶喷水推进[M]. 北京:国防工业出版社, 1988, 228-248. JIN Ping-zhong. Ship waterjet propulsion[M]. Beijing:National Defense Industry Press, 1988:228-248. |
| [2] | ALLISON J. Marine waterjet propulsion[J]. SNAME Transaction, 1993, 101:275-335. |
| [3] | Final report and recommendation to the 21th ITTC[C]//The 21th International Towing Tank Conference. Bergen and Trondheim, Norwegian:ITTC, 1996:189-209. |
| [4] | Waterjet propulsive performance prediction-waterjet inlet duct, pump loop and waterjet system tests and extrapolation[C]//Final Recommendations of the Specialist Committee on Validation of Waterjet Test Procedures to the 24th ITTC. Edinburgh, UK:ITTC, 2005:7.5-02-05-03.2. |
| [5] | ROBERT J L, WALKER G J. Boundary layer ingestion effects in flush waterjet intakes[C]//Proceedings of International Conference on Waterjet Propulsion. Amsterdam:RINA, 1998. |
| [6] |
林建忠, 阮晓东, 陈邦国, 等. 流体力学[M]. 北京:清华大学出版社, 2013:326-328. LIN Jian-zhong, RUAN Xiao-dong, CHEN Bang-guo, et al. Fluid mechanics[M]. 2nd ed. Beijing:Tsinghua University Press, 2013:326-328. |
| [7] |
雷林, 王智祥, 孙鹏, 等. 计算流体力学κ-ε二方程流模型应用研究[J]. 船舶工程, 2010, 32(3):5-8. LEI Lin, WANG Zhi-xiang, SUN Peng, et al. Application study on the turbulence mdels of κ-ε quadratic equation on CFD calculation[J]. Ship Engineering, 2010, 32(3):5-8. |
| [8] | ALEXANDER K, COOP H, VAN TERWISGAT. Waterjet-hull interaction:recent experimental results[C]//SNAME Transaction. Jersey City, New Jersey:SNAME, 1994, 102:275-335. |
 2016, Vol. 38
2016, Vol. 38
