2. 水下信息与控制重点实验室, 陕西西安 710077
2. Science and Technology on Underwater Information and Control Laboratory, Xi'an 710077, China
在采用闭式循环动力系统的水下航行器中,由于没有尾气排放,系统与外界只有热量交换而无物质交换,做功后的乏汽必须经壳体冷凝器冷凝成水后才能供给系统作为循环工质使用,所以壳体冷凝器是闭式循环系统必不可少的关键组件。
由于闭式循环水下航行器的壳体冷凝器结构限制,其内部用于冷凝换热的管路是毫米级别的小流径通道,而且小流径通道内伴随凝结的两相流动是非定常的且是不稳定的,这就使得整个换热过程的流动传热特性和能量变化规律变得极其复杂。
目前国内外学者主要针对工业用制冷行业中的冷凝换热的小通道进行了大量理论和实验研究,但对闭式循环动力系统壳体冷凝器中的小通道研究尤其是相关的实验研究却很少。
本文对小通道冷凝换热进行实验研究,分析蒸汽入口温度对水下航行器小通道换热的影响。根据实验数据确定相变点位置,并与仿真结果进行对比,修正了仿真计算模型,为闭式循环动力系统壳体冷凝器的设计提供参考。
1 实验系统及实验方法 1.1 实验装置根据壳体冷凝器中小通道具有的通流面积小,轴向长度长的结构特点,并且针对冷凝器实际工作状态设计实验装置,其结构如图 1 所示。其中实验件为双层板式结构,上层为冷却水通道,下层为 20 条蒸汽冷却通道。根据壳体冷凝器结构限制,蒸汽通道截面尺寸为 5 mm × 6 mm。过热蒸汽经导流板流入水平布置的 20 条矩形小通道,在小通道内过热蒸汽与上层的冷却水进行换热凝结成冷凝水从冷凝水出口排出。由于现场实验条件的限制,冷却水流量达不到水下航行器真实的使用环境,因此采用缩比实验方式;根据相似准则中的几何相似条件,实验件的蒸汽通道结构、几何尺寸(宽度、高度)与真实使用的冷凝器保持一致。此外在冷却水通道内部设置导流槽,尽量使冷却水均匀流动。

|
图 1 实验装置结构总图 Fig. 1 The general structure of the experimental device |

|
图 2 小通道截面图 Fig. 2 The sectional view of the small channels |
实验装置在工作时,过热蒸汽通过对流换热的方式将热量传递给蒸汽通道的上端面,然后蒸汽通道上端面经热传导将热量传递到冷却水通道下端面,最终冷却水和下端面进行对流换热将热量带走。
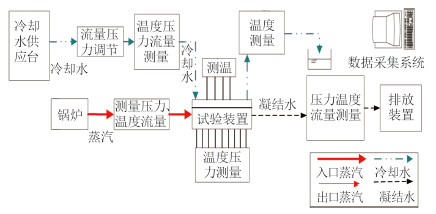
1.2 实验测量系统小通道实验测量系统如图 3 所示,从锅炉产生的过热蒸汽,进入实验系统内。同时,冷却水从管道内进入实验系统与小通道内的过热蒸汽进行换热。高温的过热蒸汽冷凝换热后凝结成水从实验系统的出口流出。通过安装在蒸汽通道进出口及沿程的温度压力传感器研究蒸汽通道内的温度压力变化。根据安装在蒸汽通道进出口的流量计监测通道进口蒸汽流量和出口的冷凝液流量。通过以上温度压力以及流量数据可以求出过热蒸汽沿管道方向的焓降、热流密度。通过测量冷却水通道内的温度和流量,可以计算出蒸汽凝结换热的对流换热系数。
|
图 3 实验测试系统图 Fig. 3 The diagram of the test system |
蒸汽流量由精度等级为 0.5 FS 的文丘里差压式流量仪测量,蒸汽进出口及沿程温度和冷却水沿程温度由Ω牌 T 型温度传感器测量,测量精度为 0.5% FS。蒸汽进口和沿程压力由麦克 MPM 480 型压力变送器测量。冷却水流量和蒸汽通道出口凝结水流量由精度等级为 0.5 级的涡轮流量计测量。测量数据由德威创数据采集系统采集。
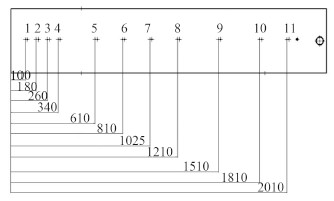
其中要考虑实验件测点布置情况,根据仿真结果的研究,在蒸汽的冷凝换热过程中,过热段和凝结段的对流换热效果最强,因此在测点的布置上要重点考虑这2个区域,在相对于蒸汽进口靠前的位置,温度压力测点布置得密一些,在过冷段,测点可布置得相对稀疏些。本次实验温度测点布置如图 4 所示。
|
图 4 蒸汽通道测点布置图 Fig. 4 The measuring point of the steam channel |
在实验件及其测控系统搭建调试完毕后进行实验研究,所要研究的实验工况为:蒸汽入口雷诺数 Re = 15 000~50 000,蒸汽进口压力为 0.15~0.25 MPa,温度为 110 ℃~190 ℃,通道蒸汽流量为 3~5 g/s。
1.3 实验数据处理 1.3.1 热平衡和质平衡1)热平衡
由于蒸汽管路与外界不可能完全绝热,实验过程中蒸汽经过系统管路和实验装置时会与外部环境进行热量交换,产生的热量损失可用相对热平衡率进行衡量。
冷却水吸收热量:
| ${Q_{sw}}{\rm{ = }}{\dot m_{sw}}c{p_{sw}}({T_{sw{\rm{,out}}}}{\rm{ - }}{T_{sw{\rm{,in}}}}), $ | (1) |
蒸汽释放热量:
| $ {Q_{cd}}{\rm{ = }}{h_{cd{\rm{,in}}}} - {h_{cd{\rm{,out}}}}{\rm{,}} $ | (2) |
相对热平衡率:
| $ \alpha = \frac{{{Q_{cd}}{\rm{ - }}{Q_{sw}}}}{{0.5({Q_{cd}}{\rm{ + }}{Q_{sw}})}} 。 $ | (3) |
2)质平衡
蒸汽通道进出口的质量平衡关系可用相对质平衡率进行衡量。
相对质平衡率:
| $ \beta {\rm{ = }}\frac{{{{\dot m}_{cd\text{,}{\rm{in}}}} - ({{\dot m}_{cd\text{,}{\rm{out}}}} + {{\dot m'}_{cd,{\rm{out}}}})}}{{0.5({{\dot m}_{cd\text{,}{\rm{in}}}} + {{\dot m}_{cd\text{,}{\rm{out}}}} + {{\dot m'}_{cd\text{,}{\rm{out}}}})}} \text{。} $ | (4) |
在蒸汽侧与冷却水侧,沿流动方向对应节点分为5段,每段节点均布置温度传感器,可测得蒸汽及冷却水沿程的温度分布。分别为:tcd1,tcd2,…,tcd11以及tsw1,tsw2,…,tsw11。在每个微元段内部,温度按照前后2个节点平均值计算:
| $ {\bar t_{cd\text{,}i}} = ({t_{cd\text{,}i}} + {t_{cd\text{,}i - 1}})/2 \text{,} $ | (5) |
| $ {\bar t_{sw\text{,}i}} = ({t_{sw\text{,}i}} + {t_{sw\text{,}i - 1}})/2 \text{。} $ | (6) |
1)冷却水侧换热系数
根据冷却水侧的 D - B 试验关联式,可获得冷却水对流换热系数:
| $ {{\mathop{Re}\nolimits} _{sw}}{\rm{ = }}\frac{{{u_{sw}}{d_{sw}}}}{{{\nu _{sw}}}} \text{,} $ | (7) |
| $ N{u_{sw}} = 0.023{\mathop{Re}\nolimits} _{sw}^{0.8}Pr _{sw}^n{(\frac{{{\eta _{sw}}}}{{\eta _{swo}^{}}})^{0.11}} \text{,} $ | (8) |
| $ {h_{sw}} = \frac{{N{u_{sw}}{\lambda _{sw}}}}{{{d_{sw}}}} \text{。} $ | (9) |
2)蒸汽侧局部换热系数
由能量守恒定律可得到每个微元段内的换热量,并导出冷却水侧壁面温度 $\bar t_{swo,j}^{}$:
| $ Q = {h_{sw\text{,}j}}{A_j}({\bar t_{swo\text{,}j}} - {\bar t_{sw\text{,}j}}) = {m_{sw}}{c_{p\text{,}sw}}({t_{sw,j + 1}} - {t_{sw\text{,}j}}) \text{,} $ | (10) |
| $ {{\bar t}_{swo.j}} = \frac{{{m_{sw}}{c_{p{\rm{,}}sw}}({t_{sw.j + 1}} - {t_{sw{\rm{,}}j}})}}{{{h_{sw{\rm{,}}j}}{A_{\rm{j}}}}} + {{\bar t}_{sw{\rm{,}}j + 1}}{\rm{。}} $ | (11) |
由壳体内部导热方程,可得到蒸汽侧壁面温度 ${\bar t_{cdo,j}}$:
| $ {\bar t_{cdo\text{,}j}} = \frac{{Q\delta }}{\lambda } + {\bar t_{swo\text{,}j}} \text{。} $ | (12) |
由蒸汽能力守恒定律可得蒸汽侧局部对流换热系数hcd,i:
| $ {h_{cd,i}} = \frac{Q}{{{A_j}({{\bar t}_{cd\text{,}i}} - {{\bar t}_{sw\text{,}j}})}} \text{。} $ | (13) |
3)小通道总传热系数
蒸汽通道侧热流密度:
| $ {q_o} = \frac{Q}{{{\rm{a}} \cdot l}} \text{。} $ | (14) |
对数平均温差:
| $ \Delta {t_m} = \frac{{\left( {{t_{cd\text{,}in}} - {t_{sw\text{,}out}}} \right) - \left( {{t_{cd\text{,}out}} - {t_{sw\text{,}in}}} \right)}}{{\ln \frac{{\left( {{t_{cd\text{,}in}} - {t_{sw\text{,}out}}} \right)}}{{\left( {{t_{cd\text{,}out}} - {t_{sw\text{,}in}}} \right)}}}} \text{。} $ | (15) |
通道换热系统总传热系数:
| $ K{\rm{ = }}{q_{\rm{o}}}/\Delta {t_m} \text{。} $ | (16) |
4)蒸汽侧换热系数
通过热阻的串联,可得:
| $ \frac{1}{K} = \frac{1}{{{h_{sw}}}}{\rm{ + }}{R_{\rm{w}}}{\rm{ + }}\frac{1}{{{h_{cd}}_{}}} \text{,} $ | (17) |
其中,冷却水侧换热系数可表达为
| $ {h_{sw}} = \frac{Q}{{{{\bar t}_{swo}} - {{\bar t}_{sw}}}} \text{,} $ | (18) |
通道壁面导热热阻可表达为
| $ {R_{\rm{w}}}{\rm{ = }}\frac{\delta }{{\lambda {}_{cd}}} \text{。} $ | (19) |
| $ {h_{cd}}{\rm{ = }}\frac{1}{{\frac{1}{K} - \frac{1}{{{h_{sw}}}} - \frac{\delta }{{{\lambda _{cd}}}}}} \text{。} $ | (20) |
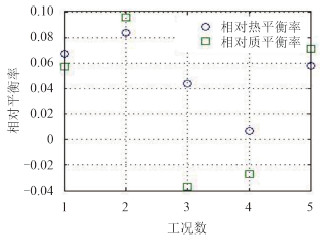
根据既定工况进行实验研究并按照上述实验数据处理方法处理实验数据,得到相对热平衡、质平衡率以及相关参数的变化曲线如图 5 所示。
|
图 5 相对热平衡率与相对质平衡率 Fig. 5 The relative heat balance rate and the relative mass balance rate |
本次实验共进行5组实验,根据每组实验数据处理可看出,相对热平衡率在 1%~8% 之间,相对质平衡率在 - 5%~9% 之间,说明实验系统散热损失基本在合理范围内,而实验系统进出口工质质量基本守恒。
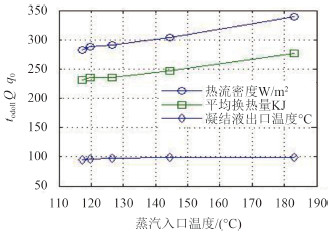
根据入口蒸汽温度的不同得到5组工况下通道内的各参数如图 6 和图 7 所示。
|
图 6 不同蒸汽进口温度通道内各参数 Fig. 6 The various parameters of the channel in different steam inlet temperature |
|
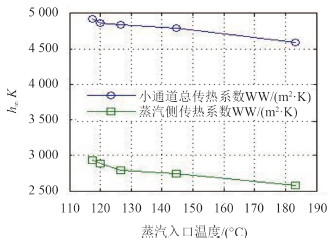
图 7 不同蒸汽进口温度通道内传热系数 Fig. 7 The heat transfer coefficient of the channel in different steam inlet temperature |
从图 6~图 7 可以看出通道总平均换热量、热流密度以及凝结水出口温度均随冷凝器入口蒸汽温度升高而升高。但通道总传热系数和蒸汽侧平均换热系数随蒸汽入口温度升高而降低。
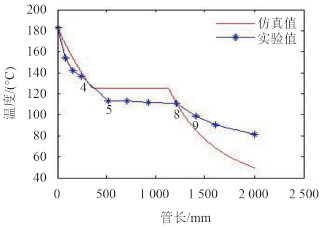
将实验工况(蒸汽入口温度 183.1 ℃,入口压力 0.24 MPa)的沿程温度分布与仿真曲线进行对比,如图 6~图 8 所示。
|
图 8 仿真与实验温度对比 Fig. 8 The temperature comparison between thesimulation and the experiment |
从图 8 可以看出,蒸汽进入小通道后与冷却水进行对流换热,在入口气相过热段,过热蒸汽迅速与外部冷却水换热并降温,当蒸汽温度降低到饱和温度时进入两相区进行相变换热,两相区的温度维持在饱和温度附近。但由于流动阻力以致两相区的温度并不完全恒定,而是有略微下降。在小流径通道后段,通道内温度又开始逐渐下降,说明已经进入液相区,此时蒸汽处于过冷状态,直至冷却通道出口。
从误差百分比图 9 中可知,过热段和两相段温度误差较小,在± 10% 以内,而过冷段温度误差较大,对应点误差最大达到 38%。根据实验数据对仿真模型进行修正,对修正后的模型计算出来的仿真值与实验值进行对比如图 10 所示。

|
图 9 仿真与实验误差百分比 Fig. 9 The error percentage of simulation and experiment |

|
图 10 修正后的仿真与实验误差百分比 Fig. 10 The error percentage of the simulation and the experiment after revised |
由图 10 可以看出,仿真值与实验值的误差最大范围缩小到 14.16%,达到合理范围。
此外由图 8 可知,在整个换热过程中,通道内蒸汽过热段和两相段的相变分界点距离蒸汽入口 500 mm 测点 4 和测点 5 之间附近,而两相段与过冷段的相变分界点在测点 8 和测点 9 之间距离进口 1 200 mm 附近。采用线性插值进行计算可知:过热段到两相段的分界点在距离进口 482 mm 附近,两相段到过冷段的分界点在距离进口 1 288 mm 附近。经过计算可知,过热段、两相段、过冷段的蒸汽侧平均凝结换热系数如表 1 所示。
|
|
表 1 蒸汽凝结过程各段平均传热系数 Tab.1 The average heat transfer coefficient of different stages of the steam condensation |
本文通过对不同蒸汽进口温度的矩形小通道冷凝器换热特性进行实验研究,得出进口温度对冷凝器换热特性的影响,并且在实验数据的基础上修正了仿真模型,使得仿真模型的最大误差 38% 下降到 15% 以内,并且确定了过热段、两相段以及过冷段的相变点位置,可以为后续设计闭式循环动力系统壳体冷凝器提供支撑和参考。
| [1] | 查志武. 鱼雷热动力技术[M]. 北京:国防工业出版社, 2006. |
| [2] | 杨玉顺. 工程热力学[M]. 哈尔滨:哈尔滨工业大学出版社, 2001. |
| [3] | 杨世铭, 陶文铨. 传热学[M]. 北京:高等教育出版社, 2006. |
| [4] |
朱晓红, 李海东, 张卫东. 船用膜式螺旋管换热器传热和流动特性研究[J]. 舰船科学技术, 2015, 37(8):165-168. ZHU Xiao-hong, LI Hai-dong, ZHANG Wei-dong. Numerical studies on heat transfer and flow of membrane spiral-tube marine heat exchanger[J]. Ship Science and Technology, 2015, 37(8):165-168. |
| [5] |
曾和义, 秋穗正, 苏光辉, 等. 宽高比对矩形窄缝通道内流体温度场的影响[J]. 核动力工程, 2008, 29(3):5-8. ZENG He-yi, QIU Hui-zheng, SU Guang-hui, et al. Effect of aspect ratio on temperature distribution of fluid in narrow rectangular channels[J]. Nuclear Power Engineering, 200829(3):5-8. |
| [6] |
李卓, 俞坚, 夏国栋, 等. 水平矩形小通道内气-液两相流流动特性的研究[J]. 流体机械, 2006, 34(8):1-5. LI Zhuo, YU Jian, XIA Guo-dong, et al. Flow characteristics of gas-liquid two-phase flow in small horizontal rectangular channels[J]. Fluid Machinery, 2006, 34(8):1-5. |
| [7] | WANG H S, ROSE J W. A theory of film condensation in horizontal noncircular section microchannels[J]. Journal of Heat Transfer, 2005, l27(10):1096-1105. |
| [8] |
邱金荣, 贾臻, 龚自力, 等. 船用换热设备选型分析及小型化技术应用[J]. 舰船科学技术, 2012, 34(10):98-101, 132. QIU Jin-rong, JIA Zhen, GONG Zi-li, et al. Research on marine heat exchanger type choice and miniaturization technology application[J]. Ship Science and Technology, 2012, 34(10):98-101, 132. |
 2016, Vol. 38
2016, Vol. 38
