2. 船舶振动噪声重点实验室, 湖北武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China
圆锥壳是水下航行器尾部的主要结构形式,对于圆锥壳振动的研究有利于减小水下航行器振动和噪声。L.Tong[1]提出一种幂级数的方法,给出各向同性和各项异性圆锥壳的自由振动解析解。Mauro Caresta[2]以幂级数法为基础,分析在低频范围内,截顶圆锥壳在流体负载条件下的振动特性。骆东平等[3]采用迁移矩阵法分析了环肋圆锥壳的自由振动特性。陈美霞[4]分析加肋的圆锥壳在水中的振动特性。朱显明等[5]通过模型试验的方法研究截顶圆锥壳的自由振动特性,并综合相关文献,分析壳体参数改变对壳体固有频率的影响。
对截顶圆锥壳固有振动特性的研究,可以了解水下航行器尾部的振动模式。
本文通过数值计算研究了幂级数法计算截顶圆锥壳各阶周向模态下前两阶固有频率的收敛性和准确性,并采用有限元法进行仿真验证。进一步讨论了壳厚、半锥角以及轴向长度等参数对圆锥壳振动特性的影响。
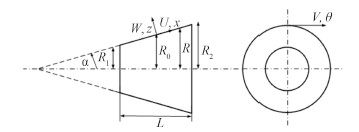
1 基本理论 1.1 圆锥壳振动方程如图 1所示,引入(x,θ)坐标系,U,V和W分别表示壳体3个方向振动的位移;圆锥壳小端中面半径R1;大端中面半径R2;轴线方向长度L;R0为壳体平均半径;R0处为(x,θ)坐标系原点,壳体任一位置处半径可表达为
| $ R\left(x \right)={{R}_{0}}+x\text{sin}\alpha, $ | (1) |
|
图 1 截顶圆锥壳模型 Fig. 1 Truncated conical shell model |
由Donnell壳体理论,圆锥壳振动方程可以表示为[6]
| $ \begin{align} & {{L}_{11}}U+{{L}_{12}}V-{{L}_{13}}W+\rho h{{\omega }^{2}}U=0, \\ & {{L}_{21}}U+{{L}_{22}}V-{{L}_{23}}W+\rho h{{\omega }^{2}}V=0, \\ & {{L}_{31}}U+{{L}_{32}}V-{{L}_{33}}W+\rho h{{\omega }^{2}}W=0. \\ \end{align} $ | (2) |
式中:ρ为壳体密度;h为壳厚;ω为壳体振动角频率;Lij为偏微分算子[1]。
由幂级数法,可以将方程(2)的解表示为
| $ \begin{align} & U=u\left(x \right)\text{cos}n\theta \text{,} \ & V=v\left(x \right)\text{sin}n\theta \text{,} \ & W=w\left(x \right)\text{cos}n\theta.\ \end{align} $ | (3) |
其中:
$ \begin{align} & u\left( x \right)=\sum\limits_{\text{m}=0}^{\infty }{{{a}_{m}}}{{x}^{m}}\text{,} \\ & v\left( x \right)=\sum\limits_{\text{m}=0}^{\infty }{{{b}_{m}}}{{x}^{m}}\text{,} \\ & w\left( x \right)=\sum\limits_{\text{m}=0}^{\infty }{{{c}_{m}}}{{x}^{m}}\text{,} \\ \end{align} $
n为壳体周向模态,am,bm和cm为相应的幂级数系数。将式(3)代入式(2)中,根据x的同次幂系数相等,可得到相应的递推公式。由此,幂级数的未知系数am,bm(m≥ 2)和cm(m ≥ 4)可用8个系数a0,a1,b0,b1,c0,c1,c2,c3表示,如式(4)所示。
| $ \begin{align} & {{a}_{m+2}}={{A}_{1}}{{a}_{m+1}}+{{A}_{2}}{{a}_{m}}+{{A}_{3}}{{a}_{m-1}}+ \\ & \ \ \ \ \ \ \ \ \ {{A}_{4}}{{a}_{m-2}}+{{A}_{5}}{{b}_{m+1}}+{{A}_{6}}{{b}_{m}}+ \\ & \ \ \ \ \ \ \ \ \ {{A}_{7}}{{c}_{m+1}}+{{A}_{8}}{{c}_{m}}\text{,} \\ & {{b}_{m+2}}={{B}_{1}}{{a}_{m+1}}+{{B}_{2}}{{a}_{m}}+{{B}_{3}}{{b}_{m+1}}+ \\ & \ \ \ \ \ \ \ \ \ \ {{B}_{4}}{{b}_{m}}+{{B}_{5}}{{b}_{m-1}}+{{B}_{6}}{{b}_{m-2}}+\ \\ & {{B}_{7}}{{c}_{m}}\text{,} \\ & {{c}_{m+4}}={{C}_{1}}{{a}_{m+1}}+{{C}_{2}}{{a}_{m}}+{{C}_{3}}{{a}_{m-1}}+ \\ & \ \ \ \ \ \ \ \ \ \ {{C}_{4}}{{a}_{m-2}}+{{C}_{5}}{{b}_{m}}+{{C}_{6}}{{b}_{m-1}}+ \\ & \ \ \ \ \ \ \ \ \ \ {{C}_{7}}{{b}_{m-2}}+{{C}_{8}}{{c}_{m+3}}+{{C}_{9}}{{c}_{m+2}}+ \\ & \ \ \ \ \ \ \ \ \ \ \ {{C}_{10}}{{c}_{m+1}}+{{C}_{11}}{{c}_{m}}+{{C}_{12}}{{c}_{m-1}}+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ {{C}_{13}}{{c}_{m-2}}+{{C}_{14}}{{c}_{m-3}}+{{C}_{15}}{{c}_{m-4}} \\ & \ \ \ \ \ \ \ \quad \quad \quad \quad \quad \quad \quad (m=0,1\text{,}2\text{,}\ldots ). \\ \end{align} $ | (4) |
式(4)中的系数A(1~8),B(1~7)和C(1~15)由壳体参数和固有频率所组成[2]。
1.2 边界条件本文考虑简支边界条件,即V=W=Nx=Mx=0,其中Nx为壳体母线方向的薄膜力,Mx为弯矩。
以X=[a0,a1,b0,b1,c0,c1,c2,c3]T作为待求向量,可以得到形如DX=0的矩阵方程,其中D为系数矩阵,令系数矩阵的行列式为0,可得到固有频率[7, 8]。
2 数值计算和有限元仿真本文的圆锥壳模型参数如下:大端中面半径R2=0.548 m;小端中面半径R1=0.233 m;壳厚h=0.002 m;轴线方向长度L=1 m;杨氏模量E=2.1×1011 N/m2;泊松比μ=0.3;密度ρ=7 800 kg/m3。
2.1 数值计算通过Matlab编制程序,计算以上模型在不同周向模态n下的前两阶固有频率,m取不同值时,计算结果如表 1和表 2所示。
|
|
表 1 各阶周向模态下第 1 阶固有频率(Hz) Tab.1 The first natural frequencies under each circumferential mode number(Hz) |
|
|
表 2 各阶周向模态下第二阶固有频率(Hz) Tab.2 The second natural frequencies under each circumferential mode number(Hz) |
m值越大,幂级数法计算的固有频率值越准确[1],为确定得到足够精度结果时m的最小值,对各阶周向模态n下,不同m值的固有频率值做多项式拟合,拟合曲线在m处的斜率为k(n,j,m),其中n=1~Nj为周向模态数,j=1,2为前2阶固有频率。其均方根Δk为
| $ {{\Delta }_{k}}=\sqrt{\sum\limits_{n\text{,}j}{\frac{1}{{{N}_{j}}}}k_{n\text{,}j\text{,m}}^{2}}. $ | (5) |
在m=11时,Δk=0.8,可见此时各条曲线斜率已近似为0,表明结果已收敛。为方便计算,本文引入不同周向模态n下相邻m值的固有频率之差的均方根Δ,即
| $ \Delta=\sqrt{\sum\limits_{n\text{,}j}{\frac{1}{{{N}_{j}}}}{{({{x}_{n\text{,}j\text{,}m}}-{{x}_{n\text{,}j\text{,}m-1}})}^{2}}}. $ | (6) |
其中x(n,j,m)为周向模态n下第j阶固有频率在m处的值,m=0,1,2,…
Δk和Δ正相关,以均方根Δ判断计算结果的收敛性。在m=11时,均方根Δ=16.5,因此,若均方根Δ≤ 16.5时,计算结果可达到收敛。
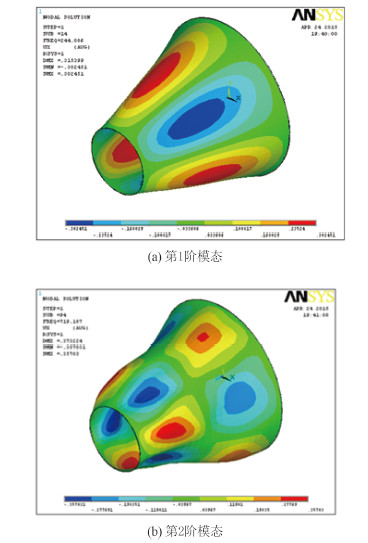
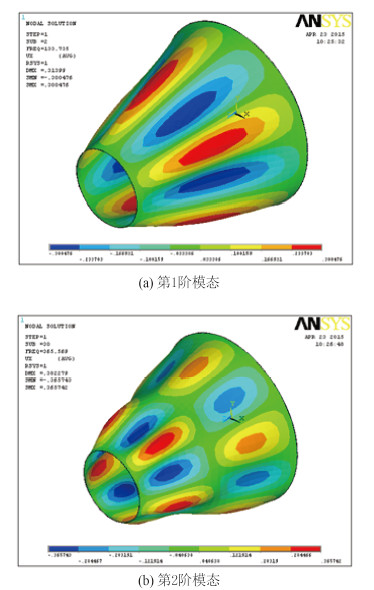
2.2 有限元仿真有限元仿真过程,在Ansys软件中采用shell63单元建立圆锥壳模型,划分网格后,进行模态分析。前2阶固有频率仿真结果见表 3。图 2和图 3分别给出了周向模态n=3和n=5时的前2阶模态结果。
|
|
表 3 各阶周向模态下前两阶固有频率仿真结果(Hz) Tab.3 The simulation results of the first two natural frequencies under each circumferential mode number(Hz) |
|
图 2 周向模态 n = 3 时模态 Fig. 2 Mode of circumferential mode number n = 3 |
|
图 3 周向模态 n = 5 时模态 Fig. 3 Mode of circumferential mode number n = 5 |
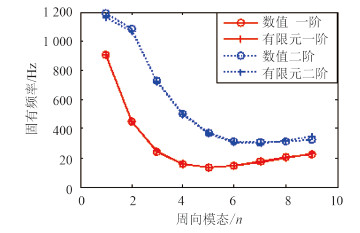
图 4是m=11时固有频率的数值计算结果和有限元仿真结果对比图,从图 4中可以看出两者十分接近。此时数值计算结果的均方根为16.5。
|
图 4 数值仿真与有限元仿真结果对比 Fig. 4 Contrastingresults of numerical calculation and the finite element simulation |
由此可见,幂级数法计算简支截顶圆锥壳各阶周向模态下前2阶固有频率,在均方根小于16.5时其结果比较准确。下文均以此作为计算标准。
3 壳体参数对固有频率的影响本文考虑了壳厚、半锥角以及轴向长度等因素对圆锥壳固有频率的影响。
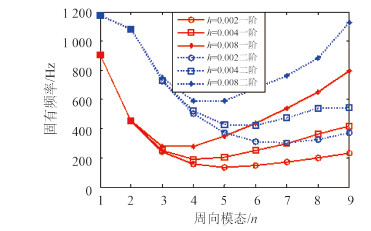
3.1 壳厚对固有频率的影响如图 5(a)所示,考虑壳厚对固有频率的影响。m=11,Δ=23.5;m=12,Δ=13.6。可见m=12时结果已收敛。如图 6所示,壳厚增大,简支圆锥壳的前2阶固有频率总体表现为增大。周向模态n=1~3时,壳厚对前2阶固有频率影响不大,周向模态n=4~9时,壳厚越大,对固有频率的影响越大。
|
图 5 壳体参数改变图 Fig. 5 The diagram of shell parameters change |
|
图 6 壳厚对固有频率的影响 Fig. 6 The effects ofthickness on the natural frequencies |
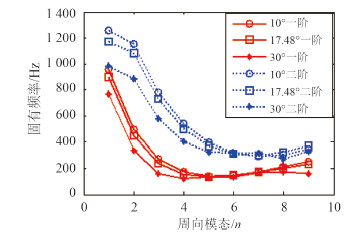
如图 5(b)所示,考虑半锥角对固有频率的影响。m=11,Δ=27.0;m=12,Δ=11.3。可见m=12时结果已收敛。从图 7中可以看出,随半锥角减小,固有频率增大,并且在周向模态数较低时,半锥角对固有频率的影响比较明显。
|
图 7 半锥角对固有频率影响 Fig. 7 The effects of semi-cone angle on the natural frequencies |
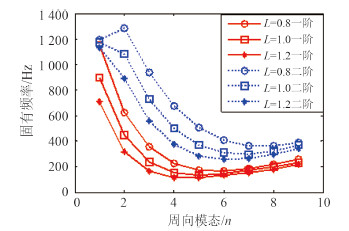
如图 5(c)所示,考虑轴向长度对固有频率的影响。m=12,Δ=19.8;m=13,Δ=12.0。可见m=13时结果已收敛。从图 8中可以看出,随轴向长度减小,固有频率增大,并且与图 7情况类似,在周向模态数较低时,轴向长度对固有频率的影响比较明显。
|
图 8 轴向长度对固有频率影响 Fig. 8 The effects of axial length on the natural frequencies |
如图 5(d)所示,同时考虑半锥角和轴向长度的影响。m=11,Δ=29.2;m=12,Δ=14.2。可见m=12时结果已收敛。如图 9所示,从图中可以看出,当半锥角α增大,壳体轴向长度L减小时,前2阶固有频率整体表现为增大,可见该过程中,与半锥角的影响相比较,轴向长度对固有频率的影响更大。另外,与图 7和图 8的情况类似,在周向模态数n较小时,两者对固有频率的影响较大。
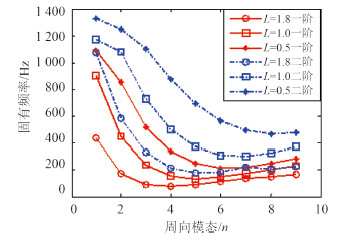
|
图 9 半锥角及轴向长度对固有频率影响 Fig. 9 The effects ofsemi-cone angle andaxial length of conical shells on the natural frequencies |
本文为研究幂级数法计算简支截顶圆锥壳前2阶固有频率,得到准确结果时,m取的最小值,提出以均方根作为收敛性的评判标准。进一步研究了壳体参数对固有频率的影响。均方根标准的提出,在保证准确性的基础上,减少了计算固有频率的时间,提高了效率。分析壳体参数对固有频率的影响,可指导壳体结构设计,避免壳体发生共振。
| [1] | TONG L Y. Free vibration of orthotropic conical shells[J]. International Journal of Engineering Science, 1993, 31(5):719-733. |
| [2] | CARESTA M, KESSISSOGLOU N J. Vibration of fluid loaded conical shells[J]. Acoustical Society of American, 2008, 124(4):2068-2077. |
| [3] | 骆东平, 赵玉喜. 环肋圆锥壳自由振动特性分析[J]. 振动与冲击, 1990(4):64-69. |
| [4] |
陈美霞, 邓乃旗, 张聪, 等. 水中环肋圆锥壳振动特性分析[J]. 振动与冲击, 2014, 33(14):25-32. CHEN Mei-xia, DENG Nai-qi, ZHANG Cong, et al. Vibration of submerged and ring stiffened conical shells[J]. Journal of Vibration and Shock, 2014, 33(14):25-32. |
| [5] | 朱显明, 张国良, 师汉民. 截顶圆锥壳体的自由振动分析[J]. 舰船科学技术, 1997(5):33-36. |
| [6] | LEISSA A W. Vibration of shells[M]. New York:American Institute of Physics, 1993. |
| [7] | CARESTA M, KESSISSOGLOU N J. Free vibrational characteristics of isotropic coupled cylindrical-conical shells[J]. Journal of Sound and Vibration, 2010, 329(6):733-751. |
| [8] | CARESTA M, KESSISSOGLOU N J. Acoustic signature of a submarine hull under harmonic excitation[J]. Applied Acoustics, 2010, 71(1):17-31. |
 2016, Vol. 38
2016, Vol. 38
