随着能源需求的增加和人们环保意识的增强,天然气作为一种清洁能源越来越受到青睐。对于液化天然气的海上长距离运输,LNG船无疑是最有效、最经济的选择。耐波性作为船舶安全性能的一个重要指标,在船舶的设计和运营过程中必须考虑。通过数值计算可以得到LNG船在波浪中的-运动响应,可以为其设计提供参考。
目前用于计算船舶运动响应的方法有二维切片方法、高速细长体理论(亦称二维半方法)、三维方法。三维方法又可以分为自由面格林函数方法和Rankine源方法。其中自由面格林函数方法求解比较复杂,而Rankine源方法求解比较简单,计算比较灵活,可以很好地用于求解有航速问题和非线性问题。
Sclavounos和Nakos[1]给出了重力波在离散化的自由面上的传播,这表明Rankine源可以用于表达船行波和力。Kring[2]在Nakos[3]工作的基础上,将Rankine源法从频域推广到用于时域有航速船波的求解。Lee等[4]基于WAMIT计算了矩形LNG船的运动响应,研究了液舱晃荡和运动响应的耦合作用。Song[5]和Kim等对基于三维弱非线性时域Rankine源方法的WISH软件进行验证,通过数值计算结果跟1艘实际的集装箱船 6 500 TEU的模型试验数据进行对比,计算结果与试验结果总体非常吻合。陈震和文俊华[6, 7]基于SESAM软件Wasim模块研究五体船不同侧体布局对运动响应的影响。孙政[8]采用对LNG船进行数值计算,并将计算结果跟试验结果进行对比,计算结果总的趋势与试验结果一致。
本文采用基于Rankine源方法的Wasim软件对LNG船在规则波中的运动响应进行计算,研究浪向和航速对其运动响应的影响。按照耐波性试验要求[9],制作船模进行试验,将计算结果跟试验结果进行对比。
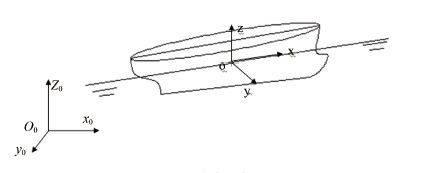
1 理论计算方法 1.1 坐标系船舶在波浪中航行时,由于波浪扰动而产生摇荡运动,基于刚体运动理论将船视为刚体,此时船则有6个自由度,即纵荡、横荡、升沉、纵摇、横摇和摇艏。为了描述船舶运动,本文引入2个坐标系,如图 1所示。1)空间固定坐标系O0x0y0z0,它固定在某一位置,x0y0平面与静水平面重合,z0轴铅直向上;2)平动坐标系oxyz,它是以船速V随船一起运动的直角坐标系,其原点位于未扰动的水面上。
|
图 1 坐标系 Fig. 1 The coordinate system |
在平动坐标系oxyz内,船舶任意时刻的运动都可以分解为船舶重心G沿3个坐标轴的直线运动以及绕轴的转动。
1.2 Rankine面元法由于Rankine源只满足拉普拉斯方程,并不满足任何边界条件,因此需要对自由面及船体表面进行网格划分,这样导致更多的未知变量和需要更大的计算内存和更多的计算时间。底面条件通过镜像的方法来满足,因此底面不需要网格离散。
根据格林第二公式可以得出在流域中的任一速度势φ均应满足[10]
| $\iiint\limits_{V}{(\phi \cdot {{\nabla }^{2}}G-G\cdot {{\nabla }^{2}}\text{ }\phi)}\text{d}V=\iint\limits_{s}{(\phi \frac{\partial G}{\partial n}-G\frac{\partial \phi }{\partial n})\text{d}s},$ | (1) |
式中G为格林函数。在这里选取Rankine源为格林函数,即G=1/rpq,rpq为p及q两点间的距离。p为场点坐标,q为源点坐标。由此上式可以变为
| $\begin{array}{*{35}{l}} {} \\ c\cdot \Phi(p)=\int{}\int\limits_{S}{(\frac{1}{{{r}_{pq}}}\cdot \frac{\partial }{\partial {{n}_{q}}}(\Phi(q))-\Phi(q)\frac{\partial }{\partial {{n}_{q}}}(\frac{1}{{{r}_{pq}}}))\text{d}s},\\ \quad \quad c=\left\{ \begin{matrix} 4\pi \quad p\in V,\\ 2\pi \quad p\in s,\\ 0,\quad \text{其他} \\ \end{matrix} \right.\\ \end{array}$ | (2) |
求解得到速度势后,根据伯努利方程,可以得到船体的表面压力分布,
| $p - {p_a}=- \rho(\frac{D}{{Dt}}\Phi+\frac{1}{2}{(\nabla \Phi)^2}+gz)\text{。} $ | (3) |
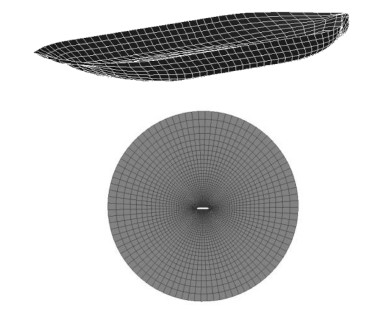
采用Rankine源方法计算LNG船在波浪中运动响应时,需要对船体表面和自由面进行网格划分。Wasim提供自动划分网格的方法,网格参数为40×12,LNG计算模型湿表面和自由面的网格如图 2所示。
|
图 2 LNG船计算模型的湿表面及自由面网格的划分 Fig. 2 The grid of wet surface and free surface of LNG ship |
LNG船的计算模型按照实船1:1的比例进行建模,模型的重量为船满载状态时的排水量,加载方式是按照耐波性试验要求进行加载。模型的具体参数如表 1所示,
|
|
表 1 LNG船计算模型的主要参数 Tab.1 Main parameters of LNG ship model |
为研究浪向和航速对其运动响应的影响,本文计算了浪向角为0°,45°,90°,135°,180°时航速分别为17.5 kn,19.5 kn是其在规则波中的运动响应。具体工况如表 2所示,
|
|
表 2 计算工况 Tab.2 the calculation conditions |
1)浪向对运动响应的影响
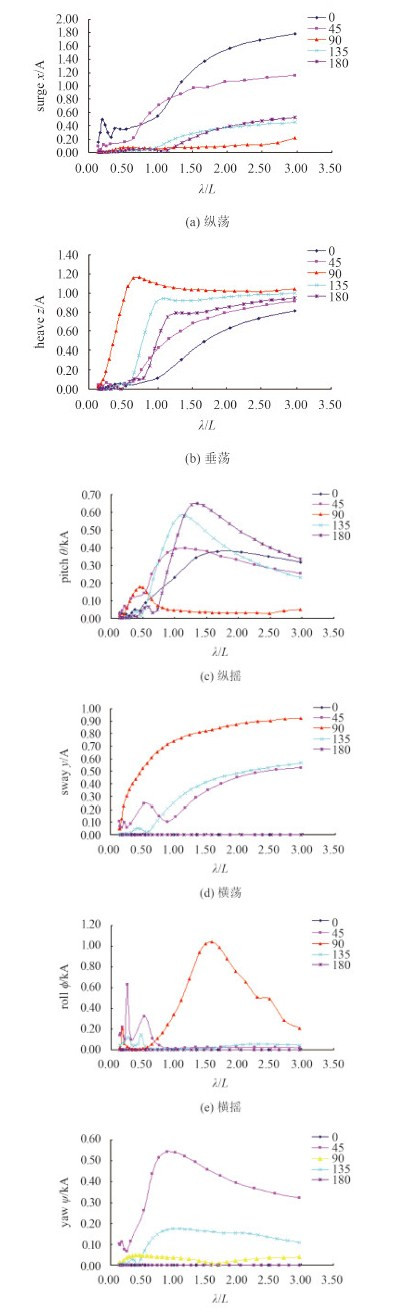
图 3为航速为Fr=0.172时各浪向情况下的六自由度运动响应传递函数。图 3(a)可以看出,随浪对纵荡的影响最大,其次是为45°时,横浪90°时纵荡很小,几乎没有影响。图 3(b)是各浪向下的垂荡响应传递函数曲线,图上可以看出,横浪的升沉响应最大,迎浪时在波长为1.25倍船长时为峰值。从趋势上看,随着波长的变大,升沉响应函数的值趋向于1。图 3(c)为各浪向情况下纵摇响应曲线,迎浪180°时纵摇响应最大,在波长为1.25倍船长时达到峰值,其次为浪向角135°。图 3(d)为横荡响应曲线,从图中可以看出,横浪时响应最大,迎浪和随浪情况的横荡为0,这与实际情况符合。图 3(e)为横摇响应曲线,横浪情况横摇响应最大,尤其是在波长为1.5倍船长时响应最大。图 3(f)为摇首运动响应曲线,在横浪、迎浪、随浪情况下响应较小。135°时响应要小于45°时的响应。
|
图 3 航速为17.5 kn时LNG船各浪向的运动响应 Fig. 3 The motion response of LNG ship at the speed of 17.5 knot to each wave direction |
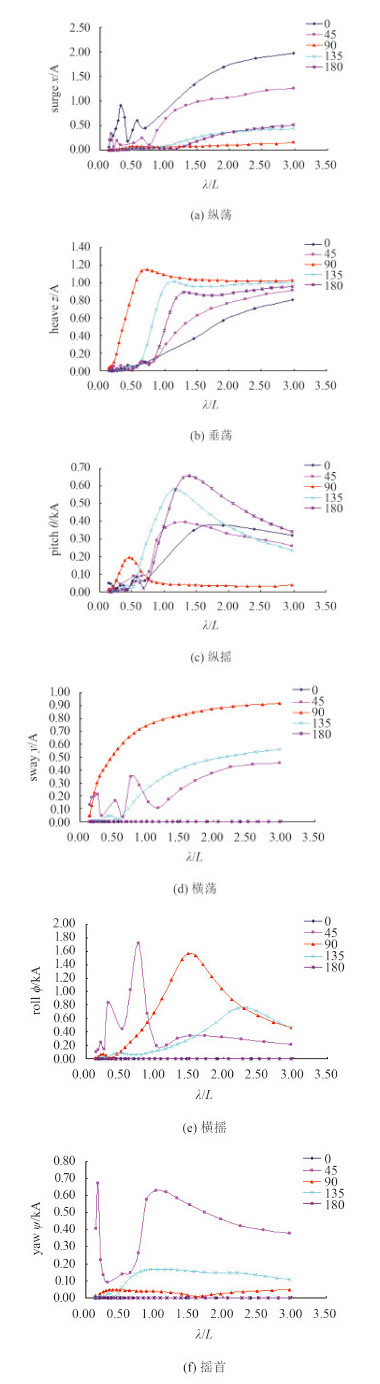
图 4为航速为19.5 kn时各浪向下的运动响应情况。从图上可以看出,LNG船在航速为19.5 kn时各浪向下的运动响应的趋势跟航速为17.5 kn时的趋势是一致的。
|
图 4 航速19.5 Kn时各浪向下的运动响应 Fig. 4 The RAOs of LNG ship at the speed of 19.5 knot to each wave direction |
2)航速对运动响应的影响
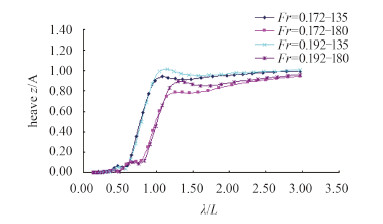
为研究航速对运动响应的影响,将航速为17.5 kn和19.5 kn的升沉和纵摇运动响应进行对比。图 5为两航速下升沉响应函数曲线,从图上可以看出,两航速下浪向角为135°和180°时的升沉频响函数曲线的变化趋势相似,航速19.5 kn时的峰值延后且值要偏大,但在短波时的值要略小于17.5 kn的值,长波时两航速的曲线趋于一致。
|
图 5 LNG船两航速下升沉频响函数曲线 Fig. 5 Heave RAOs of LNG ship under two speed |
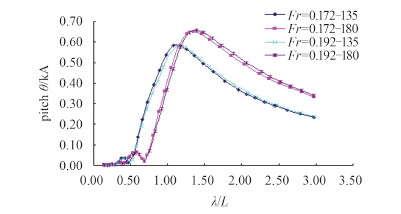
图 6为两航速下的纵摇频响函数曲线,从图中可看出,浪向角为135°和180°时的两航速下的频响函数曲线变化规律比较相似,航速19.5 kn的峰值延后且在长波时响应要偏大2%左右。
|
图 6 LNG船两航速下纵摇频响函数曲线 Fig. 6 Pitch RAOs of LNG ship under two speeds |
本次试验在华中科技大学船舶与海洋工程学院的拖曳水池进行,水池的主尺度为175 m ×6 m ×4 m。根据试验规程,试验模型是计算模型按照缩尺比1:69.5进行制作。LNG船模的具体参数如表 3所示,试验参数如表 4所示。
|
|
表 3 LNG船模参数 Tab.3 Parameters of LNG ship model |
|
|
表 4 LNG船模试验参数表 Tab.4 Parameters table of LNG ship model test |
试验的测试内容为:航速分别为1.08 m/s、1.203 m/s时不同波长情况下的纵摇、升沉以及首中尾加速度的响应幅值。图 7为LNG船模试验图。运动参数测量点:

|
图 7 LNG船耐波性试验图 Fig. 7 The picture of LNG ship model under seakeeping experiment |
首部加速度: 中线面上19站处
升沉、纵摇及中部加速度: 中线面上重心处
尾部加速度: 中线面上0站处
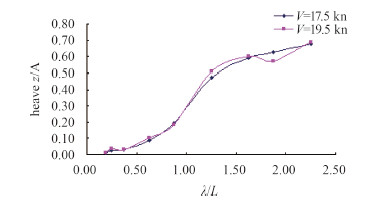
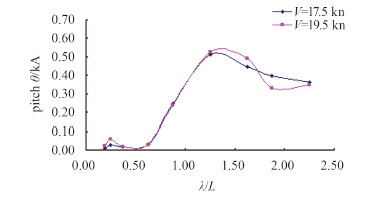
3.2 试验结果分析图 8为升沉响应频响函数曲线,图 9为纵摇频响函数曲线。从图 8可看出,两航速下的升沉响应规律比较相似,在长波时航速19.5 kn的频响函数稍大。图 9可看出,航速19.5 kn的峰值延后,且峰值稍偏大。
|
图 8 LNG船模升沉频响函数曲线 Fig. 8 Heave RAOs of LNG model |
|
图 9 LNG船模纵摇频响函数曲线 Fig. 9 Pitch RAOs of LNG model |
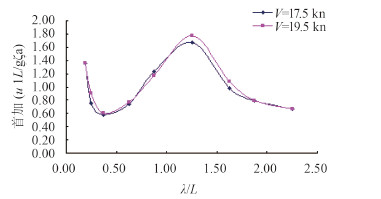
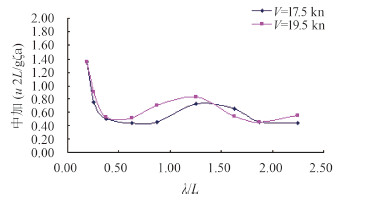
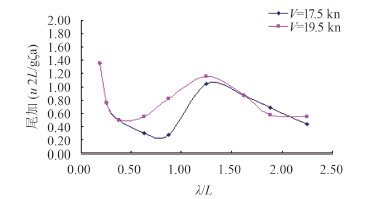
图 10 ~图 12分别为LNG船模首中尾加速度频响函数曲线。从图中可以看出,两航速下的首加、中加变化规律比较相似,尾加在短波时区别较大,长波时基本一致。总的来说,航速越大,加速度频响越大。
|
图 10 LNG船模首加频响函数曲线 Fig. 10 Front acceleration RAOs of LNG model |
|
图 11 LNG船模中加频响函数曲线 Fig. 11 Middle acceleration RAOs of LNG model |
|
图 12 LNG船模尾加频响函数曲线 Fig. 12 Stern acceleration RAOs of LNG model |
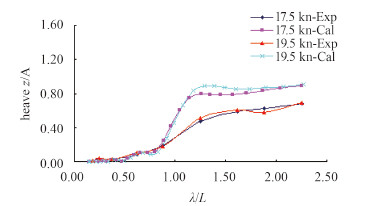
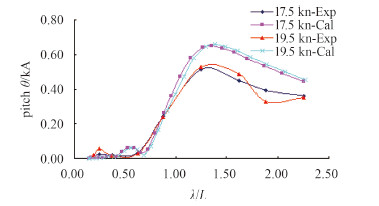
将数值计算得到的LNG船的纵摇和升沉频响函数跟试验得到的频响函数曲线进行对比,验证数值计算的可靠性。图 13为升沉响应频响函数对比图,图 14为纵摇频响函数对比图。从图 13可看出,升沉的频响函数计算结果的变化趋势与试验结果一致,只是在波浪大于船长时偏大,误差在可接受的20%以内。从图 14可看出,纵摇频响函数的计算结果变化趋势与试验结果吻合情况较好,只是峰值及以后的结果偏大,误差在15%左右。
|
图 13 升沉响应对比图 Fig. 13 Comparison of heave RAOs |
|
图 14 纵摇响应对比图 Fig. 14 Comparison of pitch RAOs |
本文计算了2个航速下LNG船在不同浪向下的六自由度运动响应,通过对比发现:1)浪向对运动响应影响较大,横浪时升沉、横摇和横荡响应最大,而迎浪时纵摇最大,浪向角为45°时摇首运动比较明显;2)相近的两航速下的升沉和纵摇频响函数变化规律相似。升沉函数曲线在短波或者长波两曲线吻合较好,迎浪19.5 kn时在波长为1.25倍船长左右的升沉响应相差稍大,在10%左右。纵摇频响函数曲线吻合很好,迎浪时19.5 kn的峰值延后0.03倍船长左右且波长大于1.5倍船长后稍大2%左右。
根据耐波性试验规程制作模型进行耐波性试验,将计算结果跟试验结果进行对比,两者的变化趋势比较吻合,如纵摇频响函数的峰值对应的波长基本一致。计算结果在长波时偏大,导致误差的原因一方面计算时没有考虑水的粘性等因素对计算结果的影响,另一方面试验时没有重复多次进行,可能存在一定的误差。对比结果说明,通过数值计算方法得到的运动响应结果可以用于船舶运动响应的预报,并可为考虑LNG船内部液舱晃荡时的运动加载提供参考。
| [1] | SCLAVOUNOS P D, NAKOS D E. Stability analysis of panel methods for free-surface flows with forward speed[C]//Proceedings of the 17th symposium naval hydrodynamics. Hague, The Netherlands:National Academy of Sciences, 1988:29-48. |
| [2] | NAKOS D E. Ship wave patterns and motions by a three dimensional rankine panel method[D]. Massachusetts, USA:Massachusetts Institute of Technology, 1990. |
| [3] | KRING D C. Time domain ship motions by a three-dimensional Rankine Panel method[D]. Massachusetts, USA:Massachusetts Institute of Technology, 1994. |
| [4] | LEE S J, KIM M H, LEE D H, et al. The effects of LNG-tank sloshing on the global motions of LNG carriers[J]. Ocean Engineering, 2007, 34(1):10-20. |
| [5] | SONG M J, KIM K H, KIM Y. Numerical analysis and validation of weakly nonlinear ship motions and structural loads on a modern containership[J]. Ocean Engineering, 2011, 38(1):77-87. |
| [6] |
陈震, 文俊华. 五体船侧体布局对纵向运动性能的影响[J]. 上海交通大学学报, 2011, 45(4):494-504. CHEN Zhen, WEN Jun-hua. The influence of side hulls layout on longitudinal motion of pentamaran in wave[J]. Journal of Shanghai Jiaotong University, 2011, 45(4):494-504. |
| [7] | 文俊华. 五体船波浪载荷和运动特性研究[D]. 上海:上海交通大学, 2012. |
| [8] |
孙政, 江克进, 王小宁, 等. 穿梭LNG船耐波性的模型试验与理论计算[C]//第十三届全国水动力学学术会议暨第二十六届全国水动力学研讨会论文集. 青岛:中国力学学会, 2014:1256-1261. SUN Zheng, JIANG Ke-jin, WANG Xiao-ning, et al. Seakeeping experiment and theoretical study of shuttle LNG carrier[C]//Proceedings of the 13th National Hydrodynamics Conference and 26th Hydrodynamics National Symposium. Qingdao:The Chinese Society of Theoretical and Applied Mechanics, 2014:1256-1261. |
| [9] | 李积德. 船舶耐波性[M]. 哈尔滨:哈尔滨工程大学出版社, 2007. |
| [10] | 戴遗山, 段文洋. 船舶在波浪中运动的势流理论[M]. 北京:国防工业出版社, 2008. |
 2016, Vol. 38
2016, Vol. 38
