随着船舶对快速性的要求越来越高,如何寻找推进效率高的推进器一直是人们探究的重点。近年来,吊舱推进器集电机和螺旋桨于一体实现了模块化设计,在船舶上的安装布置也变得灵活,目前作为主推进器一般是吊挂在船尾下方。双桨式吊舱推进器越来越受到人们的重视,随之而来的,如何预报其水动力性能和操纵性能也成为了研究的重点之一。
双桨式吊舱推进器的吊舱前后各装有一个桨,所以在桨与桨、桨与吊舱以及装在船后时与船之间的相互干扰,使得其水动力性能变得更为复杂。相比于传统推式或拖式吊舱桨,双桨式吊舱桨因后桨能吸收前桨尾流中的能量而能有效地利用更多的主机功率;相比于传统轴传动桨,前桨具有更均匀的进流比;吊舱通过支架悬挂在船体下面,体积小、重量轻、附加阻力小、效率高、空泡性能好[1, 2]。
本文采用粘流 CFD 方法对双桨式吊舱推进器敞水状态下不同偏转角时的水动力性能进行预报,希望得出预报此类吊舱推进器的一般特性。
1 CFD 原理 1.1 控制方程对于 N-S 方程的统计平均方法以及补充反映湍流特性的其他方程,如湍动能方程和湍流耗散率方程,是目前 CFD 的基本方法。
将湍流运动看作是时间平均和瞬时脉动的叠加,若不考虑瞬时脉动的影响,将 N-S 方程取时间平均,即得到雷诺平均 N-S 方程,其方程为:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}(\rho {u_i}) = 0,$ | (1) |
| $\frac{\partial }{{\partial t}}(\rho {u_i}) + \frac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} + \frac{\partial }{{\partial {x_j}}}( - \rho {\text{ }}\overrightarrow {{u_i}'{u_j}'} ).$ | (2) |
式中的 $ - \rho {\text{ }}\overrightarrow {{u_i}'{u_j}'} $ 项,成为雷诺应力项,为新的未知量,从而使得上述方程组不封闭。为封闭方程组,就必须建立有关雷诺应力项的新的方程,即湍流模型。
1.2 湍流模型由于湍流本身的复杂性,至今仍未找到一种解决湍流问题的最佳方法,而且目前关于吊舱推进器粘性流场数值计算方面的可供参考文献较少,用来封闭 RANS 方程的湍流模型中,理论上发展比较完善的有标准 k-ε 模型、RNG k-ε 模型及 SST k-ω 模型。
黄胜等[3]对湍流模型的选用做了相应研究,表明标准 k-ε 模型对螺旋桨水动力性能的数值预报存在明显的缺陷;RNG k-ε 模型相对于标准 k-ε 模型有所改变,但这种改进仍然没有抛弃基于涡粘性假设的基础,因此其对预报精度的改进有限。
钱正芳等[4]做了不同湍流模型在吊舱推进器性能计算中的应用与比较方面的研究,通过3种湍流模型的计算结果与实验数据的比较,分析在吊舱推进器数值模拟过程中湍流模型的适应性影响。结果表明,SST k-ω 湍流模型综合了 k-ω 湍流模型在近壁面计算的优点和 k-ε 湍流模型在远场计算的优点,同时增加了横向耗散导数项,在湍流粘度定义中考虑了湍流剪切应力 的输运过程,其预报吊舱推进器敞水性能的精度较高。
SST k-ω 模型为了使标准 k-ω 模型在近壁面区有更好的精度和算法稳定性而发展起来,因此本文采用 SST k-ω 模型。SST k-ω 两方程湍流模型如下:
$ \begin{gathered} \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial t}} = {P_k} - \frac{{\rho {k^{3/2}}}}{{{l_{k - \omega }}}} + \frac{\partial }{{\partial {x_i}}}[(\mu + \frac{{{\mu _t}}}{{{\sigma _k}}})\frac{{\partial k}}{{\partial {x_i}}}],\hfill \\ \begin{array}{*{20}{l}} {\frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial t}} = {\alpha _2}\frac{\omega }{k}{P_\omega } - {\beta _2}\rho {\omega ^2} + \frac{\partial }{{\partial {x_i}}}[(\mu + \frac{{{\mu _t}}}{{{\sigma _{{\omega ^2}}}}})\frac{{\partial k}}{{\partial {x_i}}}] + } \\ {\quad \quad \quad \quad \quad \quad 2\rho (1 - {F_1})\frac{{{\sigma _{{\omega ^2}}}}}{\omega }\frac{{\partial k}}{{\partial {x_i}}}\frac{{\partial \omega }}{{\partial {x_i}}}.} \end{array} \hfill \\ \end{gathered} $
式中:PK 和 Pω 为湍流生成项;F1 为混合函数;S 为剪应力张量的常数项;σK,α2,β2,σω2 均为经验系数,σK = 2,α2 = 0.44,β2 = 0.082 8,σω2 = 0.856;涡黏系数 μt 由下式确定:
$ {\mu _t} = \frac{{{\rho ^*}{\alpha _1}k}}{{\max ({\alpha _1}\omega ,S{F_2})}}. $
式中α1为待定常数。
1.3 数值计算模型多参考系模型(MRF)是将不同旋转或移动速度的每个区域进行稳态近似,因此当边界上流动区域几乎均匀混合时,这种方法比较适宜,特别是在转子和定子之间的交互作用相对较弱的时候。MRF 模型的整个计算域被分为多个小的子域,控制方程在每个子域内分别计算求解,在子域的交界面上则通过速度换算成绝对速度的形式进行各个子域流场信息的交换。但要精确模拟瞬态流场时,MRF 模型无能为力,可以求助于滑移网格。
2 计算模型 2.1 螺旋桨模型本文研究的是双桨式吊舱推进器,其吊舱前后各装有 1 部桨。采用 ICEM 建模的方法创建螺旋桨几何模型,缩尺比为 1:10,螺旋桨模型的主要几何参数如表 1,创建的三维模型如图 1 所示。
|
|
表 1 螺旋桨主要几何参数 Tab.1 The main geometric parameters of propeller |

|
图 1 前后桨模型 Fig. 1 Model of fore and aft propellers |
由于螺旋桨几何外形的复杂性,建立单一计算域划分结构或非结构网格都十分困难。本文采用结构-非结构混合网格进行离散,分块建立计算域,在 ICEM 上对吊舱单元进行网格划分,对计算域划分为3个区域:包含前桨叶的圆柱体旋转域 1、包含后桨叶的圆柱体旋转域 2 以及包含舱体和支柱的静止域 3,见图 2。在2个旋转域中对螺旋桨进行局部加密,提高计算结果的精确度;在域 3 上采用结构化网格,达到减少计算网格的目的。
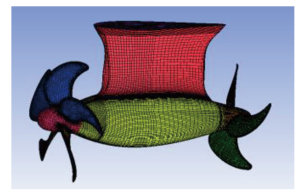
|
图 2 计算模型 Fig. 2 Calculation model |
对于此类双桨式吊舱推进器,因为前桨、后桨及舱体支柱之间的相互干扰作用,后桨在前桨尾流中运动,并受到舱体和支柱的影响,其流动是非常复杂的,因此数值计算时参数的设定对计算精度的影响非常大。本文前后桨均采用多参考系模型,计算域如图 3 所示。入口边界设置为速度入口,进速系数的变化通过改变来流速度实现,出口设置为压力出口,物面设置为无滑移表面,基于压力变量的 SIMPLE 耦合求解器,对流项和扩散项采用二阶迎风差分格式进行离散,并用发展比较完善的 SST k-ω 湍流模型进行数值模拟,由于前后桨直径不同,以前桨为基准取进速系数,前后桨桨模转速均为 n = 1 500 r/min。通过偏转全回转推进器模型来实现偏转工况的计算。

|
图 3 计算域网格划分 Fig. 3 The computational domain mesh |
由于资料有限,未能找到类似类型的双桨式吊舱桨的试验资料,为验证计算方法的精度和可行性,对某船[5]的 VP 1458/VP 1459 单桨吊舱进行数值预报,将计算值与实验值相比较,如表 2 所示。
|
|
表 2 计算值与试验值比较 Tab.2 Comparison between the calculated results and test results |
从计算结果来看,无论是推力系数 KT,还是转矩系数 10 Kq,其预报都较为准确。推力系数的误差不大于 4.3%,转矩系数的误差不大于 3.95%,从而验证了计算方法的精度和可行性,可以用来预报双桨式吊舱推进器的水动力性能。
3.2 给定工况及参数定义在敞水下选取不同的偏转攻角,分别为 0°,± 15°,± 30°,取不同的进速系数,得出不同攻角、不同进速系数 J 下前后桨的推力系数、扭矩系数以及吊舱单元的推力系数、转矩系数和横向力系数等。其中
进速系数:$J = {V_m}/(n{D_{FP}}(n{D_{FP}})$,
前桨推力系数:${K_{{T_{FP}}}} = {T_{FP}}/(\rho {n^2}(\rho {n^2}D_{FP}^4)$,
后桨推力系数:${K_{{T_{AP}}}} = {T_{AP}}/(\rho {n^2}(\rho {n^2}D_{FP}^4)$,
推进器轴向推力系数:${K_{{T_X}}} = {T_X}/(\rho {n^2}(\rho {n^2}D_{FP}^4)$,
推进器横向推力系数:${K_{{T_Y}}} = {T_Y}/(\rho {n^2}(\rho {n^2}D_{FP}^4)$,
前桨扭矩系数:${K_{{Q_{FP}}}} = {Q_{FP}}/(\rho {n^2}(\rho {n^2}D_{FP}^5)$,
后桨扭矩系数:${K_{{Q_{AP}}}} = {Q_{AP}}/(\rho {n^2}(\rho {n^2}D_{FP}^5)$,
推进器转矩系数:${K_{{M_Z}}} = {M_Z}/(\rho {n^2}(\rho {n^2}D_{FP}^5)$,
推进器敞水效率:$\eta = J{K_{{T_X}}}2\pi ({K_{{Q_{FP}}}}[2\pi ({K_{{Q_{FP}}}} + {K_{{Q_{AP}}}})]$。
式中:Vm 为来流速度,ρ 为流体密度,下标 FP 为前桨,下标 AP 为后桨。其中,各个力与力矩的定义分在2个坐标系上,一个是固定在吊舱推进器上的移动坐标系 o-xyz,x 轴定义为从后桨向前桨为正,y 轴定义为从后桨向前桨看时指向左侧为正,z 轴满足右手定则;另一个坐标系 O-XYZ 为固定坐标系,不随吊舱的偏转而偏转,它在 0°偏转角时,与 o-xyz 重合,两坐标系之间的关系如图 4 所示,偏转角如图所示时为正[6]。

|
图 4 两个坐标系 Fig. 4 Two coordinate systems |
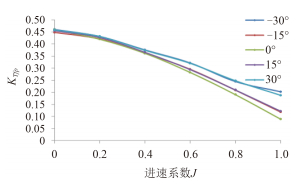
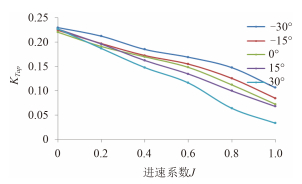
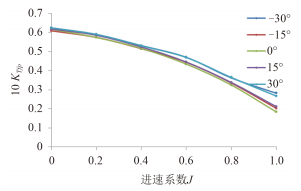
图 5~图 8 给出不同偏转角下,前后螺旋桨的推力系数与扭矩系数随进速系数的变化曲线图。
|
图 5 不同偏转角时前桨推力系数曲线 Fig. 5 The thrust coefficient curves of fore propellers at different deflection angles |
|
图 6 不同偏转角时后桨推力系数曲线 Fig. 6 The thrust coefficient curves of aft propellers at different deflection angles |
|
图 7 不同偏转角时前桨扭矩系数曲线 Fig. 7 The torque coefficient curves of fore propellers at different deflection angles |

|
图 8 不同偏转角时后桨扭矩系数曲线 Fig. 8 The torque coefficient curves of aft propellers at different deflection angles |
图 5 与图 7 分别给出不同偏转角时前桨的推力系数与扭矩系数随进速系数的变化曲线,可以看出前桨推力系数与扭矩系数随偏转角的增大而增大,在低进速时变化不明显,在高进速时差距增大。随着偏转角的增大,推力系数与扭矩系数增大,但左右偏转角时的推力基本相同。其变化趋势与常规同等螺距螺旋桨敞水特性比较相符,表明舱体与后桨对前桨的影响相对较小。图 6 与图 8 给出的是不同偏转角时后桨的推力系数与扭矩系数随进速系数的变化曲线,可以看出后桨推力系数随着偏转角从负变正而逐渐减小。其变化趋势相对前桨较为平缓,其负荷几乎只为前桨的一半,说明后桨受前桨和舱体的影响较大。
图 9 ~图 14 给出不同进速系数下,前后螺旋桨的推力系数与扭矩系数随偏转角变化的曲线图。

|
图 9 不同进速系数时的前桨推力系数 Fig. 9 The thrust coefficient curves of fore propellers at different advance coefficients |
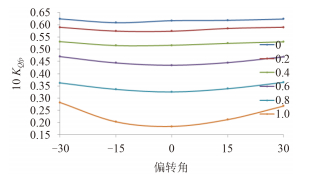
|
图 10 不同进速系数时的前桨扭矩系数 Fig. 10 The torque coefficient curves of fore propellers at different advance coefficients |
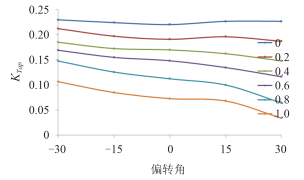
|
图 11 不同进速系数时的后桨推力系数 Fig. 11 The thrust coefficient curves of aft propellers at different advance coefficients |
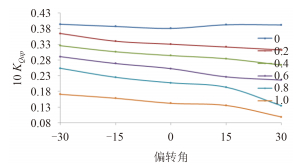
|
图 12 不同进速系数时的后桨扭矩系数 Fig. 12 The torque coefficient curves of aft propellers at different advance coefficients |
|
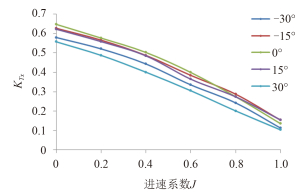
图 13 吊舱推进器推力系数 Fig. 13 The thrust coefficient of pod propulsion |
|
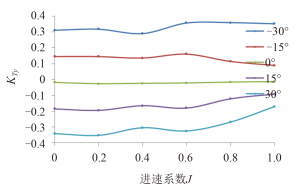
图 14 吊舱单元横向力系数 Fig. 14 The lateral force coefficient of pod propulsion |
图 9 与图 10 分别给出不同进速系数时前桨推力系数与扭矩系数随偏转角变化的曲线图,可以看出在同一偏转角下前桨推力扭矩系数都随着进速系数的增大而减小;在同一进速系数下前桨推力扭矩系数都随着左右偏转角的增大而增大,是因为随着螺旋桨的偏转,有效进速系数逐渐减小。
图 11 与图 12 分别给出不同进速系数时后桨推力系数与扭矩系数随偏转角变化的曲线图。与前桨的变化规律不同,后桨的推力扭矩系数随偏转角从负到正而减小,进速系数越大,减小的趋势月明显。原因是后桨处于前桨和吊舱后,前桨的偏转、尾流的加速、旋转和压力分布的变化以及舱体的阻塞对后桨水动力性能产生的影响。
前桨推力、扭矩系数在左右偏转角相同时几乎相等,即左右偏转时对前桨的影响对称,表明前桨的来流均匀,受后桨及吊舱体的影响很小;后桨推力、扭矩系数在左偏转时比右偏转时大,即左右偏转时对后桨的影响非对称,表明前桨的偏转、尾流的加速、旋转以及舱体的阻塞在左右偏转时对后桨的影响也非对称。
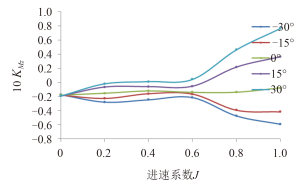
3.4 吊舱单元水动力特性图 13 ~图 16 依次给出吊舱单元推力系数、横向力系数以及转矩系数随舵角和进速系数的变化。
|
图 15 吊舱单元转矩系数 Fig. 15 The torque coefficient of pod propulsion |
|
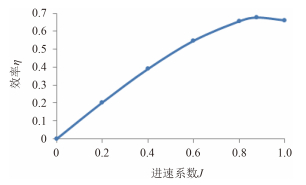
图 16 0° 偏转角时吊舱推进器的敞水效率 Fig. 16 Pod thrusters open water efficiency at deflection of 0° |
在每个工况下,随着进速系数的变化,吊舱推进器推力系数都几乎成线性下降;推力系数随偏转角的增大而减小。
由于螺旋桨的旋转,使得吊舱推进器受到横向力,但由于前后螺旋桨旋向不同,横向力相互抵消了一部分,所以在直流工况下,吊舱推进器横向力系数很小;随着偏转角的增大,横向力增大,且横向力方向与偏转角方向相同。
在 0° 偏转角时,吊舱推进器扭矩系数很小,几乎为0。在低进速系数时,吊舱推进器扭矩系数都为负。随着偏转角的增大,吊舱推进器扭矩系数增大,扭矩的方向与偏转角的方向一致。
图 16 给出吊舱推进器在直流工况下的敞水效率曲线,在 J = 0.877 8 时,效率最大,达到 0.677。
4 结语本文以双桨式全回转吊舱推进器为对象,采用RANS方法预报全回转吊舱推进器在不同偏转角度下的水动力性能,得出其推力系数、转矩系数、及横向力系数,研究结论主要有以下几点:
1)吊舱舱体对前桨与后桨都有一定的影响,但对后桨的影响比较大,原因是后桨处于前桨和吊舱后,前桨尾流的加速、旋转和压力分布的变化以及舱体的阻塞对后桨水动力性能产生的重要的影响。
2)吊舱推进器的横向力与扭矩均随着偏转角的增大而增大,推力则随偏转角的增大而减小。
3)与传统桨舵推进系统相比,全回转吊舱推进器有着更好的操舵效果,使舰船有着更好的机动性、操纵性,能实现原地回转甚至倒车。
在所进行的工况下,吊舱推进器水动力性能随偏转角和进速系数的变化规律清晰,可为全回转吊舱推进器的设计以及实船应用提供一定的参考。
| [1] |
熊鹰, 盛立, 杨勇. 吊舱式推进器偏转工况下水动力性能[J]. 上海交通大学学报, 2013, 47(6):956-961. XIONG Ying, SHENG Li, YANG Yong. Hydrodynamics performance of podded propulsion at declination angles[J]. Journal of Shanghai Jiaotong University, 2013, 47(6):956-961. |
| [2] | REICHEL M. Manoeuvring forces on azimuthing podded propulsor model[J]. Polish Maritime Research, 2007, 14(2):3-8. |
| [3] |
黄胜, 王超, 王诗洋. 不同湍流模型在螺旋桨水动力性能计算中的应用与比较[J]. 哈尔滨工程大学学报, 2009, 30(5):481-485. HUANG Sheng, WANG Chao, WANG Shi-yang. Application and comparison of different turbulence models in the computation of a propeller's hydrodynamic performance[J]. Journal of Harbin Engineering University, 2009, 30(5):481-485. |
| [4] |
马骋, 张旭, 钱正芳, 等. POD推进器技术发展及其应用前景[J]. 船舶工程, 2007, 29(6):25-29. MA Cheng, ZHANG Xu, QIAN Zheng-fang, et al. Technology development and its application prospect of POD thrusters[J]. Ship Engineering, 2007, 29(6):25-29. |
| [5] | GÜNTHER B. Resistance test, propulsion test and wake measurement[R]. Potsdam:SVAtech GmbH, 2006:13. |
| [6] |
贺伟, 陈克强, 李子如. 串列式吊舱推进器操舵工况水动力试验研究[J]. 华中科技大学学报(自然科学版), 2015, 43(1):107-111. HE Wei, CHEN Ke-qiang, LI Zi-ru. Experimental research on hydrodynamics of tandem podded propulsor in azimuthing conditions[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2015, 43(1):107-111. |
 2016, Vol. 38
2016, Vol. 38
