串列螺旋桨是一种将2部普通螺旋桨装于同一尾轴上的特种推进器。与普通螺旋桨相比，在总盘面比相同，负荷较重或直径受限制时，串列螺旋桨的效率有着相当提高，并能改善船舶尾部的震动；与其他特种推进器相比，其构造简单，易于制造加工和检验维修^[1]。事实上，20世纪60年代以前相当长的一段时间内串列螺旋桨并没有得到发展。之后，考虑到船舶振动和节能，国内外学者对串列螺旋桨产生新的兴趣，相继做了一些研究^{[2, 3]}，也取得一些进展。但总体来说，目前国内外关于串列螺旋桨的研究仍较少，只有少量模型系列试验和设计图谱，对其水动力性能进行数值模拟的研究更是少之又少。近年来，由于船舶主机功率的急速增大，推进器负载和燃料消耗不断提高，空泡、振动、噪声和节能问题更加突出，再加之普通螺旋桨的研究日趋成熟，串列螺旋桨以其突出优点可望得到发展。

近十几年来，随着计算机技术的推广普及和计算方法的不断增多，计算流体力学（CFD）技术取得了蓬勃发展，在工程领域已得到广泛应用。同时，采用 RANS 方程数值求解普通螺旋桨敞水性能的研究已开展起来^{[4, 5, 6, 7, 8]}。文中利用在船舶系统水动力性能预报方面得到广泛认可的 Fluent软件对串列螺旋桨的水动力性能进行数值模拟，得出不同进速系数下桨叶的敞水性能曲线，并将计算结果与理论值进行对比分析。同时，数值模拟也显示出了螺旋桨桨叶处及流场内的速度分布情况。

通过对参考水域的旋转处理以及给平均来流设以相对速度。可认为螺旋桨轴向和周向均相对静止的处于定常不可压流体中，则流场的连续方程和动量方程分别为：

方程中的雷诺应力项属于新的未知量，因此要使方程封闭，必须对该应力项作某种假设，即建立应力的表达式（或引进新的湍流模型方程），通过表达式或湍流模型，把应力项中的脉动值与时均值联系起来^[9]。

虽然已有大量学者们对湍流问题开展研究，但由于湍流内在机理的复杂性，迄今尚未认定一种解决螺旋桨粘性绕流场数值计算中湍流问题的最佳方法。文中选取理论上发展较为完善，在工程上广泛运用的 k-ε 湍流模型的一种 RNG（renormalization group）k-ε来封闭 RANS 方程。与标准 k-ε 模型相比，RNG k-ε 模型通过修正湍动粘度，考虑了平均流动中的旋转及旋流流动情况；其产生项不仅与流动情况有关，而且在同一问题中也是空间坐标的函数。所以 RNG k-ε 模型不但对充分发展的湍流依然有效，而且可以更好地处理高应变率及流线弯曲程度较大的流动。

RNG k-ε 模型是由 Yakhot 和 Orzag 把重整化群（RNG）方法引入到湍流研究中建立的一个新的湍流模型，其方程如下：

湍流粘性为：

本文以标准 CLB4-55-1 串列螺旋桨^[3]为例进行串列桨的水动力性能预报分析，其主要参数如表 1 所示。

表 1(Tab.1)

表 1 CLB4-55-1 串列螺旋桨的几何参数 Tab.1 Dimensions of CLB4-55-1 Tandem Propeller 主要参数 前桨 后桨 叶型 B型 B型 盘面比 0.55 0.55 叶数Z 4 4 厚度比t/D 0.045 0.045 壳径比d/D 0.182 0.182 桨距比L/D 0.21 螺距比P2/D 1.2 叶错角θ  23.7°

表 1 CLB4-55-1 串列螺旋桨的几何参数 Tab.1 Dimensions of CLB4-55-1 Tandem Propeller

与普通螺旋桨类似^[9]，模型建立于直角坐标系。X 轴定义为螺旋桨的旋转轴，正方向指向下游与来流方向相同；Y 轴定义为螺旋桨桨叶的叶面参考线方向，由叶根指向叶稍；Z 轴满足右手定则。螺旋桨叶面、叶背各个半径处以及桨毂上的型值点由自编 Fortran 语言程序计算得到，对桨叶叶根及叶梢处型值点进行必要的插值修正和补充，以特定格式导入 ICEM 前处理软件，并用 NURBS 样条曲线去拟合处理型值点，由点到线，由线到面，由面到体，合成体前先保证了桨的封闭性，最终得到光顺的三维串列螺旋桨模型，如图 1 所示。

图 1 螺旋桨三维图 Fig. 1 The three dimension chart of the propeller

网格划分是直接影响模拟精度和效率的关键因素之一，高质量的网格是实现数值模拟成功的首要条件，过密或过疏的网格都应避免。过疏会导致数值解不精确，或使计算结果不收敛。而过密的网格则使得计算量大幅度增加，对计算机硬件要求提高，计算时间延长。鉴于非结构的舍去网格节点的结构性限制，节点和单元的任意分布；容易控制网格的大小和节点的密度；具有良好的贴体性及自适应性等特点。本文选用了非结构网格对螺旋桨和内域进行划分以提高精度，如图 2 所示。

图 2 螺旋桨桨叶与桨毂网格划分 Fig. 2 Grid division of blade and hub

进速系数J分别取为0.5，0.7，0.833，0.9，1.1，螺旋桨转速为 n = 600 r/min，并以改变来流流速大小来实现进速系数的变化。计算得到的压力通过桨叶表面的积分后得到不同进速系数下的螺旋桨桨叶的推力和扭矩值，换算得到推力系数 K_t 和转矩系数 K_q。并与试验值进行比较。表 2 列出了在不同进速系数时的螺旋桨推力与扭矩。

表 2(Tab.2)

表 2 计算值与试验值对比 Tab.2 Comparison of the computed and experimental results J 试验值10 Kq 计算值10 Kq 相对误差 试验值Kt 计算值Kt 相对误差 0.4 0.828 0.798 3.62% 0.46 0.433 5.87% 0.5 0.766 0.725 5.35% 0.418 0.406 2.87% 0.6 0.704 0.672 4.55% 0.372 0.349 6.18% 0.7 0.64 0.612 4.38% 0.328 0.309 5.79% 0.8 0.576 0.54 6.25% 0.28 0.262 6.43% 0.9 0.498 0.479 3.82% 0.232 0.224 3.45% 1 0.412 0.399 3.16% 0.178 0.171 3.93% 1.1 0.316 0.305 3.48% 0.118 0.114 3.39%

表 2 计算值与试验值对比 Tab.2 Comparison of the computed and experimental results

从表 2 和图 3 可以看出不同进速系数下，串列螺旋桨的推力系数 K_t 曲线和转矩系数 K_q 曲线的计算值和理论值有一致的变化趋势、图形基本吻合，在进速系数分别为：0.5，0.7，0.833，0.9，1.1 时，K_t、K_q 的平均误差分别为 4.24% 和 4.55%，在实际工程允许范围内。尤其在螺旋桨负载较轻、进速系数大于 0.9 时，曲线吻合程度更为理想。因而验证了本文给出的串列螺旋桨水动力性能数值模拟方案的可行性和准确性。推力系数的计算结果和转矩系数的计算结果总体偏小，可能由于文章所建立的模型与理论模型几何形状不完全相同，以及所用的离散格式和求解方法等因素对结果的影响共同造成的。总体而言，计算结果与理论值之间吻合很好，可以满足工程需要。

图 3 螺旋桨的敞水性能曲线 Fig. 3 The curves of propeller’s open water performance

由于串列螺旋桨两桨之间相互干扰作用，使周围流场受到较大的影响。为更好地了解串列螺旋桨周围流场的运动情况，本文给出相同来流速度下（V = 1 m/s）情况下，串列螺旋桨沿轴向的4个截面处的速度分布，包括前桨盘面（x = 0处）、两桨之间（x = 0.1处）、后桨盘面（x = 0.2处）和尾流区（x = 0.32处）。

在图 4中，由于假定桨为静止，故水流速度相对于桨为负值；切向速度在贴近桨叶区域从叶根到叶稍逐渐增大；对比 x = 0 和 x = 0.2 两截面能发现，后桨盘面处的切向速度明显小于前桨，这是由于考虑前桨周向干扰速度的影响，后桨的来流得到周向加速，相对于水流来说要比前桨转的慢。

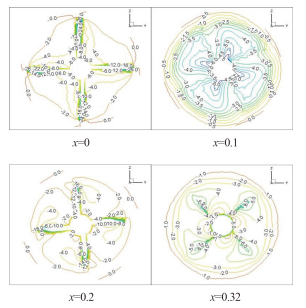
图 4 切向速度分布 Fig. 4 Tangential velocity distribution

从图 5可以看出，轴向速度在各截面沿展向都呈现先增大再减小的趋势。对比 x = 1 和 x = 0.32 两截面处能发现尾流场处轴向速度略大于两桨之间处；而对于前、后桨盘面处，轴向速度均受到来自对方和自己的轴向干扰速度影响故相差并不明显。

图 5 轴向速度分布 Fig. 5 Axial velocity distribution

本文运用计算流体动力学理论，采用 RNG k-ε 湍流模型，结合 RANS 方程，对串列螺旋桨多个进速系数下的水动力性能进行数值模拟，由上述分析得到以下结论：

1）与实验数据的比较可以发现，在螺旋桨的工作点附近，无论是推力系数还是扭矩系数，计算结果都和试验数据吻合很好，表明 CFD 技术对串列螺旋桨敞水性能的计算有较高的预报精度，能较好地满足工程需要。

2）对于进速系数大于 0.9 的情况下，螺旋桨负载较小，推力系数和转矩系数的计算结果更接近于试验值，具有更高的准确性。

3）串列螺旋桨前桨的旋转使水流的运动状态从直线流动变为边流动边旋转，因而使后桨的来流得到周向加速，所以后桨相对于水流来说周向速度明显小于前桨 ，即相对转速低于前桨。