水下结构物的主要载荷是承受深水静压力，这一受力特性决定了其耐压结构采用横剖面为圆形的薄壳结构，同时为了有效地提高耐压结构的稳定性，还必须在壳板上设置一系列横向加强筋（肋骨）。因此，从结构力学的角度来看，水下结构物的耐压船体主要是以一系列横向肋骨加强的环肋圆柱壳。虽然耐压船体钢板厚度较大，但其直径较大，属于薄壁结构。解决这一问题的经典板壳理论解法主要有解析法、数值法和半解析法。由于环肋圆柱壳结构的复杂性，采用纯解析的方法求解非常困难。随着计算机技术的发展，有限元法在船体结构分析中已占主导地位，并已成为数值解法的典型代表。由于有限元法把连续的结构离散成若干个几何形状规则的理想单元，所以能够解决复杂的高次静不定问题。但有限元法计算结果的精确与否，直接依赖于软件使用的合理性和网格划分的准确性，所以又必须以经典的板壳理论作支撑。

壳体结构（即使是薄壳结构）的稳定性问题就其本质来说，应该归属于非线性理论范畴，但是一些重要的基本结果仍然是从线性理论中获得。薄壳结构的分支点问题可以用线性理论判别其特征。目前工程计算中大多仍是以线性理论解为基础，依靠大量试验的结果得出某种规律，给出各类近似的修正公式。当前对于线性理论解的研究，采用的主要方法有能量法、传递矩阵法等。

随着现代力学、计算数学和计算机技术的发展，数值计算无论在理论，还是在计算技术方面都取得了巨大的进步。常用的数值计算方法包括有限元法、有限差分法和边界元法，而有限元法基于全离散的原理，可分析复杂结构屈曲和结构的复杂非线性屈曲问题，因此成为壳体结构屈曲分析（尤其是非线性屈曲分析）的首要手段。

本文依据船舶结构力学基础理论，通过对理想底部简支和悬臂薄壁圆柱壳的受力状态进行分析，同时建立有限元模型进行仿真计算并与理论计算结果加以比对，分析不同计算方法对于圆柱壳力学性能结果的影响。

工程中，最大厚度远小于中面曲率半径和另外2个方向尺寸的壳体称为薄壳，薄壳理论是 19 世纪末在基尔霍夫−乐甫假设的基础上建立起来的。在薄壳理论中，如果壳体的几何形状和表面载荷都是连续可微函数，则壳体处于无弯矩的应力状态，此称之为柱壳的无矩理论^[1]。

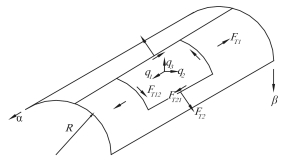
如图 1 所示，q₁，q₂，q₃分别为柱壳所受载荷分别在纵向、环向及法向的分量；F_T1，F_T2及F_T12 = F_T21分别为纵向拉压力、环向拉压力及平错力，则柱壳的无矩理论平衡方程由下式给出^[2]：

图 1 柱壳的无矩理论 Fig. 1 Non-distance theoretical of cylindrical shell

弹性方程由下式给出：

式中：u，v，w分别为柱壳中面内各点的纵向、环向及法向位移。

现假设一各向同性材料的悬臂圆柱壳，其弹性模量为E，泊松比μ，密度为ρ，长为l，R-r = Δ，一端固支，一端自由，如图 2 所示。

图 2 悬臂圆柱壳 Fig. 2 Cantilevered cylindrical shell

取圆柱壳中点为坐标原点，因为左右两边对称，所以只对 α 正方向进行计算，每单位面积的载荷为 q₀ = ρδg，q₁ = 0，q₂ = q₀sinφ，q₃ = q₀cosφ，由式（1）得：

${F_{T2}} = R{q_3} = R{q_0}{\rm{cos}}\varphi $

${F_T}_{12} = - 2{q_0}\alpha {\rm{sin}}\varphi ,0 \le \alpha \le l/2 - {l_1}$

${F_T}_{{\rm{12}}} = {\rm{2}}{q_0}\left( {l - \alpha - {\rm{2}}{l_{\rm{1}}}} \right){\rm{sin}}\varphi ,l/2 - {l_1} \le \alpha \le l/2$

$\left\{ {\begin{array}{*{20}{l}} {{F_{T1}} = }&{\frac{{{q_0}\cos \varphi }}{R}\left[{{{\left( {\frac{l}{2} - {l_1}} \right)}^2} - {\alpha ^2}} \right]}\ \\ {}&{0 \le \alpha \le \frac{l}{2} - {l_1};}\ \\ {{F_{T1}} = }&{\frac{{{q_0}\cos \varphi }}{R}\left[{{\alpha ^2} - (l - 2{l_1})\alpha + 3{{\left( {\frac{l}{2} - {l_1}} \right)}^2}} \right]}\ \\ {}&{\frac{l}{2} - {l_1} \le \alpha \le \frac{l}{2}}\ {}&{} \end{array}} \right.$

因此，对于悬臂圆柱壳在自身重力作用下，柱壳任一点纵向、环向及法向变形量u，v，w由下式给出^[3]：

式中：α 为圆柱壳上任意一点距固定端的距离，自由端 α = l^[4]；

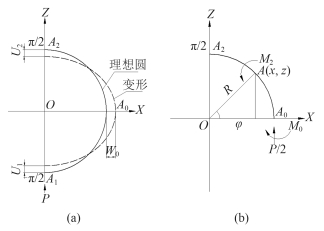
如图 3 所示，圆柱壳卧置在平台上，A 为圆柱壳上任意位置的截面，M₀，M₁为作用于圆柱壳任意截面 A 的弯矩。取纵向右半圆的圆柱壳进行分析，薄壁圆柱壳的截面厚度远小于曲率半径，作用于筒体任意截面 A 的垂直力对弯矩M的影响甚微^[5]，故省略计算。

图 3 底部简支圆柱壳 Fig. 3 Bottom simply supported cylindrical shell

A₀ 截面：X₀ = R，Z₀ = 0；A₂截面：X₂ = 0，Z₂ = R；A 截面：X = Rcosφ，Z = Rsinφ。M₂ 为第Ⅰ象限 A₂ 至 A 的圆柱壳自重作用于 A 截面的弯矩，P/2 是平台对右半圆圆柱壳的反作用力传递到 A₀ 截面的值。设第Ⅰ象限的圆柱壳于 A₀ 截面处固定之，则在 M₂ 作用下，A₂ 分别向下和向左位移^[6]。

式中：F为圆柱壳的截面积；γ为材料比重。

圆柱壳下半圆的第Ⅳ象限，设第Ⅳ象限的圆柱壳于 A₀ 截面处固定之，则在 M₁ 作用下，A₁ 分别向上和向左位移。P/2 是第Ⅰ象限圆柱壳的自重作用于 A₀ 截面的值，M₁ 为平台对右半圆圆柱壳向上的反作用力 P 和第Ⅳ象限圆柱壳向下的自重，共同作用于任意截面 A 的弯矩。

则分别作用于第Ⅰ和第Ⅳ象限的弯矩相等M₁ = M₂ = M。即作用于圆柱壳任意截面 A 的弯矩相等^[7]。

以第Ⅳ象限为例计算弯矩M值：令ε₀ = 0，$\omega =-\frac{RM}{EI}$。其中，ε₀为线应变，ω为角应变。由于理想圆柱壳，其截面 A₀ 和 A₁ 之间的夹角，自重变形后仍为直角，故 A₀ 和 A₁ 之间的角度改变Δφ₁ = 0。

垂直方向的自重变形量 U 是指垂直位置的圆柱壳中径在垂直方向的减少量。第Ⅳ象限 A₁ 点在垂直方向往上的位移 U₁：

正号表示圆柱壳的最低点 A₁ 垂直向上位移，垂直位置的圆柱壳中径在垂直方向的减少量 U 由下式给出^[8]：

其中：I 为圆柱壳的截面惯性矩；E 为材料弹性模量。

随着计算机技术的发展，有限元法在船体结构分析中已占主导地位^[9]，目前主要有MSC/Ansys/ Abaqus等大型通用有限元软件，本文通过Ansys建立典型圆柱壳有限元模型，计算底部简支及悬臂圆柱壳变形问题。

1）理想圆柱壳底部简支状态的自重变形

选取圆柱壳的直径分别为 4 000 mm，5 000 mm，6 000 mm，圆柱壳壁厚为 20 mm，30 mm，40 mm 共 9 种计算工况。材料属性为 ρ = 7.85 × 10^-9 t/mm³，E = 2.1 × 10⁵ MPa，μ = 0.3。模型边界条件为底部简支，对整个模型施加 g = 9 800 mm/s²的重力载荷。9种计算工况下圆柱壳变形仿真计算结果如表 1 和图 4 所示，有限元仿真解与有矩理论值对比如表 2 所示。

表 1(Tab.1)

表 1 底部简支圆柱壳仿真计算结果 Tab.1 Simulation calculation results of bottom simply supported cylindrical shell 壁厚/mm >直径4 000/mm >直径5 000/mm >直径6 000/mm 20 75.2 183.4 380.3 30 33.4 81.6 169.2 40 18.8 45.9 95.3

表 1 底部简支圆柱壳仿真计算结果 Tab.1 Simulation calculation results of bottom simply supported cylindrical shell

图 4 底部简支的理想圆柱壳垂直变形量随直径和壁厚变化曲线 Fig. 4 Vertical deformation of bottom simply supported cylindrical shell under different diameter and thickness

表 2(Tab.2)

表 2 简支圆柱壳垂直变形有限元仿真解与有矩理论值对比 Tab.2 The constrast of analytical method and numerical method 直径/mm 4 000 5 000 6 000 壁厚/mm 20 30 40 20 30 40 20 30 40 仿真解/mm 75.2 33.4 18.8 183.4 81.6 45.9 380.3 169.2 95.3 有矩理论解/mm 83.8 37.2 20.9 204.7 90.9 51.1 424.5 188.6 106.1 相对误差/% 10.33 10.22 10.05 10.41 10.23 10.18 10.41 10.29 10.18

表 2 简支圆柱壳垂直变形有限元仿真解与有矩理论值对比 Tab.2 The constrast of analytical method and numerical method

仿真计算结果表明底部简支的理想圆柱壳在自身重力作用下垂直变形量随内径的增大而增大，随厚度的增大而减小。同时，仿真解与理论解的差值控制在 10% 左右，且圆柱壳直径越小，厚度越大，即圆柱壳变形值越小，计算误差越小。

2）悬臂圆柱壳的自重变形

为研究悬臂圆柱壳的自重变形，依然选取圆柱壳的直径分别为 4 000 mm，5 000 mm，6 000 mm，圆柱壳壁厚为 20 mm，30 mm，40 mm 共 9 种计算工况，自由端变形量的仿真结果如表 3 和图 5 所示，有限元仿真解与无矩理论值对比如表 4 所示。

表 3(Tab.3)

表 3 悬臂圆柱壳仿真计算结果 Tab.3 Simulation calculation results of cantilevered cylindrical shell 壁厚/mm 直径4 000/mm 直径5 000/mm 直径6 000/mm 20 0.335 0.253 0.209 30 0.335 0.253 0.209 40 0.335 0.253 0.209

表 3 悬臂圆柱壳仿真计算结果 Tab.3 Simulation calculation results of cantilevered cylindrical shell

图 5 悬臂圆柱壳端面变形量随直径和壁厚变化曲线 Fig. 5 Surface deformation of cantilevered cylindrical shell under different diameter and thickness

表 4(Tab.4)

表 4 悬臂圆柱壳端面变形有限元仿真解与无矩理论值对比 Tab.4 The constrast of analytical method and numerical method 直径/mm 4 000 5 000 6 000 壁厚/mm 20 30 40 20 30 40 20 30 40 仿真解/mm 0.335 0.335 0.335 0.253 0.253 0.253 0.209 0.209 0.209 无矩理论解/mm 0.330 0.330 0.330 0.247 0.247 0.247 0.203 0.203 0.203 相对误差/% 1.52 1.52 1.52 2.43 2.43 2.43 2.96 2.96 2.96

表 4 悬臂圆柱壳端面变形有限元仿真解与无矩理论值对比 Tab.4 The constrast of analytical method and numerical method

从仿真结果可知，对于自身重力作用下的悬臂圆柱壳，仿真解与理论解误差较小，且自由端的变形量随圆柱壳内径的增大而减小，与圆柱壳厚度无关，同一端面各点的变形量大致相同，即对于悬臂圆柱壳，重力载荷对自由端面圆度影响不大。由式（4）可知，不同圆柱壳厚度Δ下，无矩理论给出的变形量结果一致，这是因为无矩理论将此类圆柱壳假设为薄壁圆柱壳，忽略了圆柱壳厚度对自由端变形的影响，仿真结果与理论解具有极高的一致性，表明该假设合理。

本文采用无矩理论及有矩理论对理想圆柱壳的变形进行分析，通过有限元方法对典型圆柱壳变形仿真计算并与理论值进行对比，得出以下结论：

1）无矩理论适用于一端固支，一端自由的圆柱壳自重变形计算，有矩理论仅适用于圆柱壳为理想圆柱壳，底部简支的情况；

2）对于一端固支，一端自由的圆柱壳，仿真结果表明，自由端的变形量随圆柱壳直径的增大而减小，与圆柱壳厚度无关，同一端面各点的变形量大致相同，即重力载荷对自由端面圆度影响不大，这与经典无矩理论规律一致；

3）对于理想圆柱壳底部简支的情况，仿真结果表明，圆柱壳在自身重力作用下，垂直位置的圆柱壳中径在垂直方向的减少量随直径的增大而增大，随厚度的增大而减小，变形量基本上与内径的四次方成正比，与厚度的二次方成反比，这与经典有矩理论规律一致；

4）对于复杂圆柱壳结构，圆柱壳的几何形状和所受载荷不再是连续可微函数，理论计算具有较大的局限性，限元方法较为合理准确。