| 莺歌海盆地中深层储层孔隙度定量预测方法研究 |
目前,莺歌海中深层高温高压气藏已进入开发阶段,该区主要目的层具有高地温梯度、高压力系数特征[1-5],储层类型复杂,砂体叠置,储层边界不清,储层物性预测十分关键。通过岩石物理理论基础可知,储层物性除了受温压条件影响外,还受到许多因素的影响,诸如岩性、孔隙度、泥质含量等等[6],这些参数的变化最终都会体现到地震反射振幅的变化上。本文首先从岩石物理分析出发,确定莺歌海盆地中深层储层物性变化主要影响因素。其次,开展储层孔隙度定量预测技术研究,建立该区振幅-孔隙度预测关系,达到孔隙度定量预测的目的。为该区中深层甜点储层预测及开发布井提供有力支持。
1 理论基础岩石物理分析技术在储层预测和烃类检测中发挥着十分关键的作用,通过岩石物理分析能够获得储层物性及含气性敏感参数,支撑后期储层物性评价及含气性预测。
储层物性和含气性分析首先需要进行骨架重构和流体替换研究,其理论基础是Gassmann方程[7-8],表达式如下:
| $\frac{{{K_{{\rm{sat}}}}}}{{{K_{{\rm{ma}}}} - {K_{{\rm{sat}}}}}} = \frac{{{K_{{\rm{dry}}}}}}{{{K_{{\rm{ma}}}} - {K_{{\rm{dry}}}}}} + \frac{{{K_{{\rm{ff}}}}}}{{\phi \left( {{K_{{\rm{ma}}}} - {K_{{\rm{fl}}}}} \right)}} $ | (1) |
式中:ϕ为孔隙度,小数。可以看到,利用上述方程,能建立饱和流体下矿物模型与孔隙度的关系,在上述方程中,Ksat、Kma、Kdry、Kfl分别代表饱和岩石、基质矿物颗粒、干岩骨架以及流体的体积模量,GPa。
Zimmerman(1991)[9]开展了在孔隙压力不变的情况下饱和岩石可压缩性Ksat-1的相关研究,并提出以下方程:
| $\frac{1}{{{K_{{\rm{sat}}}}}} = \frac{1}{{{K_{{\rm{ma}}}}}} + \frac{\phi }{{{{\tilde K}_\phi }}} $ | (2) |
| ${\tilde K_\phi } = {K_\phi } + \frac{{{K_{{\rm{ma}}}}{K_{{\rm{fl}}}}}}{{{K_{{\rm{ma}}}} - {K_{\rm{f}}}}} \approx {K_\phi } + {K_{{\rm{fi}}}} $ | (3) |
式中:
上述公式表明,Ksat由Kφ(与孔隙度相关的孔隙刚度)、Kma(矿物颗粒体积模量)以及Kfl(孔隙之中的流体模量)决定,而Kφ、Kma、Kfl分别对应着模型的孔隙度、泥质含量、以及含水饱和度。因此,在含水饱和度不变的情况下,通过改变骨架中的泥质含量和孔隙度即可实现对Ksat变化的研究;也就是说,在含水饱和度不变的情况下,通过泥质含量、孔隙度的变化能最终实现地震反射振幅变化的研究。
2 高温高压条件下物性影响因素分析本次研究目标区为莺歌海盆地X区中深层高温高压气藏。为了了解高温高压气藏的特征,首先对该区已钻井进行测井曲线分析(图 1),从图中可以看出,该区储层段主要呈现低GR、低纵波速度、低密度、低纵波阻抗的特征,利用纵波阻抗能够有效区分储层段和泥岩段。
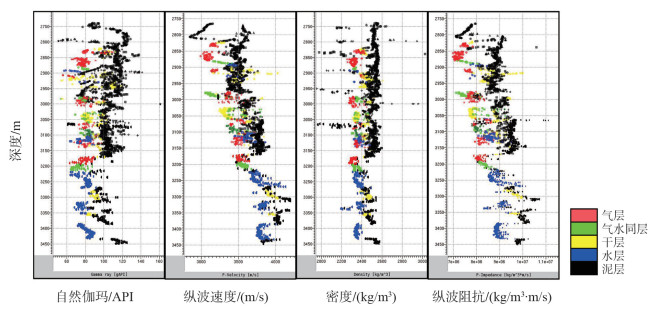 |
| 图 1 X区中深层测井曲线分析图 |
掌握该区高温高压储层的岩石物理特征后进行储层物性研究。通过前面的理论介绍可知,在含水饱和度不变的情况下,通过改变骨架中的泥质含量和孔隙度即可实现对岩石物性变化的研究,即以泥质含量为出发点,孔隙度为媒介,能最终反映到岩石骨架速度与密度变化当中。在本次研究中,首先利用GR测井曲线计算泥质含量,利用中子测井和密度测井曲线计算孔隙度。然后用岩心资料进行标定以得到最终的总孔隙度和有效孔隙度。计算得到泥质含量曲线和总孔隙度曲线后进行交汇分析和曲线拟合,从图 2可以看到,孔隙度与泥质含量相关关系良好,随着泥质含量的增加总孔隙度逐渐降低,气层、水层、干层和泥岩在拟合趋势线上归位良好。
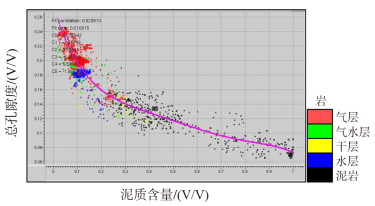 |
| 图 2 孔隙度与泥质含量交会分析图 |
东方X区高温高压条件下孔隙度与泥质含量拟合关系式如下:
| ${\phi _{\rm{t}}} = 0.275\;542 - 1.077\;99{v_{{\rm{sh}}}} + 3.565\;31{v_{{\rm{sh}}}}^2 - 6.417\;62{v_{{\rm{sh}}}}^3 + 5.596\;82{v_{{\rm{sh}}}}^7 - 1.869{v_{{\rm{sh}}}}^5 $ | (4) |
式中:ϕt为孔隙度,小数;vsh为泥质含量,小数。
获得孔隙度随泥质含量变化的关系式后,即可通过增加模型中砂岩段的泥质含量和与之对应减少的孔隙度来搭建储层物性变化研究模型,进而拟合不同泥质含量(岩性)下的纵波速度与密度,最终模拟地震反射振幅变化。
3 正演模拟及实例应用选取X区井况良好的A井进行实际正演模拟。在测试层段分别采取泥质含量为10%(原始值)、13%、18%计算孔隙度,从图 3可以看到,砂岩孔隙度随着泥质含量的增加而减少,砂岩的速度和密度随着泥质含量的增加而明显增加。通过测试段孔隙度变化与纵波阻抗变化交汇分析(图 4)表明,计算的纵波阻抗与孔隙度呈线性负关系,纵波阻抗随着孔隙度的增大而减小,也就是说,在泥岩背景阻抗值不变的条件下,储层孔隙度越高,纵波阻抗越低,储层顶面地震反射振幅绝对值越大。
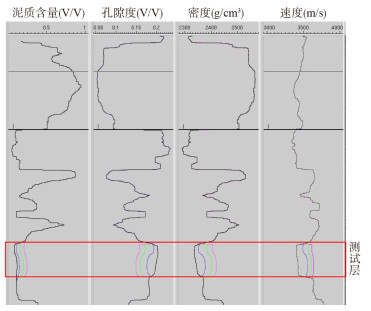 |
| 图 3 孔隙度、密度、速度随泥质含量变化分析图 |
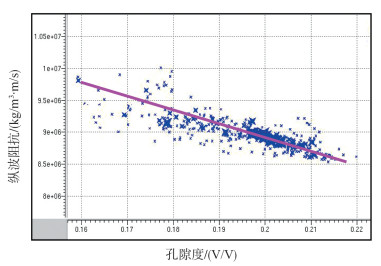 |
| 图 4 X区中深层纵波阻抗与孔隙度交会分析图 |
接下来,进行地震正演模拟,A井原始孔隙度为21%,原始振幅为-6.53。从正演模拟结果可以看到(图 5),在其它条件保持不变的情况下,随着孔隙度减小,地震反射振幅也减弱;也就是说,储层物性变差后,储层顶面反射系数响应变小,即储层反射强度降低。另外通过定量分析得到:当泥质含量为10%、孔隙度为17.5%的情况下,振幅为-3.27;当泥质含量为18%、孔隙度为15%的情况下,振幅为-1.62;这两种情况下振幅比值2.02,也就是说孔隙度减小2.5%,反射振幅减弱1/2。
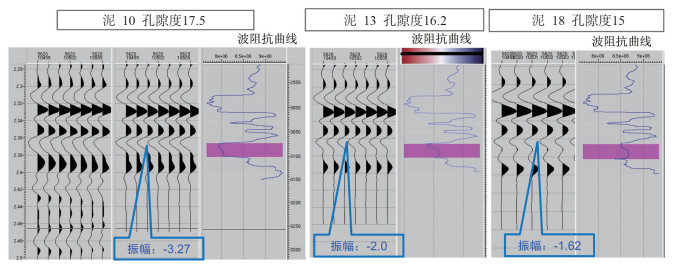 |
| 图 5 随泥质含量变化振幅分析图 |
除了对A井的正演模拟外,利用该区B井进行有效性测试及误差分析。B井气顶振幅为-3.2,根据上述关系,推测孔隙度为17.6%,实际孔隙度为18%,误差为0.4%个孔隙度,误差整体较小,满足研究需要。
基于上述分析可知,在该区可以利用储层顶面反射强度进行物性预测,波谷振幅绝对值越大,孔隙度越高,若振幅绝对值增大两倍,孔隙度增加2.5%。有了以上分析及认识后,接下来基于实际地震资料对X区储层顶面振幅进行分析,并将其转化为孔隙度预测剖面,将上述物性研究结果应用到X区实际地震资料的储层物性预测中。图 6为该区主要目的层气层顶面孔隙度属性预测图,从图中可以看到,扇体前缘孔隙度低,预测为泥岩,该区泥质水道发育,水道侵蚀切割将砂体分割成不同的区块,与此同时,该套目的层砂体发育,存在多个甜点区块,在已钻井(紫线代表已钻井位置)所在位置北边存在高孔隙度区域,可以作为该区勘探开发布井的方向。
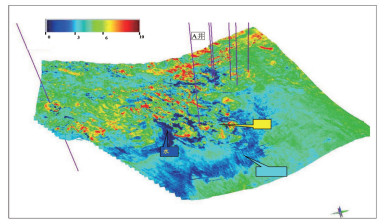 |
| 图 6 X区孔隙度预测平面图 |
4 结论
通过改变骨架中的泥质含量和孔隙度实现对岩石物性变化的研究。研究表明,砂岩孔隙度随着泥质含量的增加而减少,砂岩的速度和密度随着泥质含量的增加而明显增加;随着孔隙度减小,地震反射振幅也减弱。在该区可以利用储层顶面振幅强度进行物性预测,波谷振幅绝对值越大,孔隙度越高,若振幅绝对值增大两倍,孔隙度增加2.5%。将上述物性研究结果应用到X区实际地震资料的储层物性预测中,预测该区目的层砂体发育,存在多个甜点区块,可作为下一步勘探开发布井方向。本文开展的高温高压条件下储层物性影响因素研究及储层物性定量预测技术研究,为高温高压条件下“甜点”预测提供支持,同时为莺歌海盆地勘探开发布井提供指导。
| [1] |
谢玉洪, 范彩伟. 莺歌海盆地东方区黄流组储层成因新认识[J]. 中国海上油气, 2010, 22(6): 355-359,386. DOI:10.3969/j.issn.1673-1506.2010.06.001 |
| [2] |
周家雄, 李芳, 马光克, 等. 利用密度差值识别和预测莺歌海盆地高温高压气藏[J]. 石油物探, 2014, 53(5): 609-616. DOI:10.3969/j.issn.1000-1441.2014.05.015 |
| [3] |
马光克, 李芳, 周家雄, 等. 高温高压欠压实地层烃类检测方法研究:以莺歌海盆地东方X区为例[J]. 地质科技情报, 2015, 34(6): 221-225. |
| [4] |
李芳, 邓勇, 刘仕友, 等. 欠压实低速泥岩对地震反射及AVO的影响[J]. 地质科技情报, 2017, 36(5): 244-248. |
| [5] |
李芳, 周凡, 李洋森, 等. 高温超压地层随钻声波速度预测方法研究[J]. 海洋石油, 2019, 39(1): 61-65. DOI:10.3969/j.issn.1008-2336.2019.01.061 |
| [6] |
李维新, 史謌, 王红, 等. 岩石物理弹性参数规律研究[J]. 地球物理学进展, 2007, 22(5): 1380-1385. DOI:10.3969/j.issn.1004-2903.2007.05.007 |
| [7] |
Gassmann F. Elastic Waves Through A Packing of Spheres[J]. Geophysics, 1951, 16(4): 673-685. DOI:10.1190/1.1437718 |
| [8] |
Biot M A. Theory of Propagation of Elastic Waves in A FluidSaturated Porous Solid. I. Low-Frequency Range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [9] |
Zimmerman R W. Elastic Moduli of A Solid with Spherical Pores:New Self-Consistent Method[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1984, 21(6): 339-343. |
 2019, Vol. 39
2019, Vol. 39

