2. 福州大学空间数据挖掘与信息共享教育部重点实验室, 福州 350108;
3. 卫星空间信息技术综合应用国家地方联合工程研究中心, 福州 350108
2. Key Lab of Spatial Data Mining and Information Sharing of Ministry of Education, Fuzhou University, Fuzhou 350108;
3. National & Local Joint Engineering Research Center of Satellite Geospatial Information Technology, Fuzhou 350108
近年来, 以PM2.5为重要组分的雾霾污染高度频发, 给人类生活和生态环境带来了严重危害(王秦等, 2013).精准的PM2.5小时浓度预测能够为实际空气污染预警提供技术支持, 是当前空气污染预报和防治的重要研究方向(尹建光等, 2018).目前空气污染物浓度预测模型大致分为机理模型和非机理模型两种(郭晓雷, 2011).在非机理模型中, 面向大数据的深度学习方法表现较好(孙宝磊等, 2017).深度学习方法中, 循环神经网络(RNN)可处理PM2.5序列在时间上的依赖性, 具有良好的预测性能, 但随着网络层数的增加, 可能存在梯度消失(爆炸)或历史信息损失等问题.长短期记忆神经网络(LSTM)在传统RNN模型中引入门控制机制, 解决了RNN模型中存在的长时依赖等问题(Li et al., 2017).近年来, 以LSTM网络建立的PM2.5时序预测模型取得了较好的效果, 例如, Zhao等(2019)以空气污染物和气象因子的历史数据为输入, 建立了LSTM-FC模型;Wen等(2019)以PM2.5的时空特征为输入, 建立了时空C-LSTM模型.但在PM2.5预测模型中仍存在以下2个问题:①影响因素的考虑不够全面, 预测模型的输入变量较为单一.如黄婕(2018)仅以PM2.5的时空特征为预测模型的输入, 没有考虑气象因素和其它空气污染物对PM2.5的影响;Bai等(2019)仅以气象因素为预测模型的输入, 忽略了PM2.5的空间相关性.②影响因素选择方法适用性不强, 且很难选出最优的影响因素组合作为预测模型的输入变量.在已有的PM2.5预测方法中, 输入变量的选取是根据某种固定的评价准则或根据经验知识从PM2.5的多个影响特征中进行选择, 难以选出最优的影响特征.
自动编码器(Auto-Encoder, AE)是一种无监督训练的神经网络模型, 可以从高维特征中自动学习低维抽象特征, 已在语音识别(Hinton et al., 2012)、模式识别(Zhang et al., 2017)等领域中得到了较好的应用.栈式稀疏自编码器(SSAE) (Mandi et al., 2018; Gnouma et al., 2019; Jia et al., 2019)是在传统自编码器的基础上增加一些稀疏性约束得到的, 是一种更具鲁棒性的通用型特征提取方法.SSAE可通过无监督的方式学习多维PM2.5影响特征中存在的依赖关系, 自动提取PM2.5低维抽象特征, 为后续建立PM2.5时序预测模型提供重要的特征信息.
本文综合考虑时间因素、空间因素、气象因素和空气污染物因素等多种PM2.5影响因素, 研究一种融合SSAE深度特征学习和LSTM网络的新型网络模型, 模型以PM2.5的多种影响因素为输入特征, 利用SSAE网络从输入特征中自动提取低维抽象特征, 并将抽象特征输入至LSTM网络, 实现PM2.5小时浓度预测.模型综合考虑了多种因素对PM2.5的影响, 能同时对多个站点进行协同训练和预测, 解决了传统预测方法需对每个站点进行逐个训练和预测的问题, 可为实际PM2.5小时浓度精准预测提供一定的理论依据和技术参考.
2 方法(Methods)本研究提出一种融合SSAE和LSTM网络的新型网络模型SSAE-LSTM, 用于PM2.5小时浓度预测, 模型结构如图 1所示.模型主要由输入数据层、SSAE特征学习层、LSTM预测层、输出层4个部分组成.
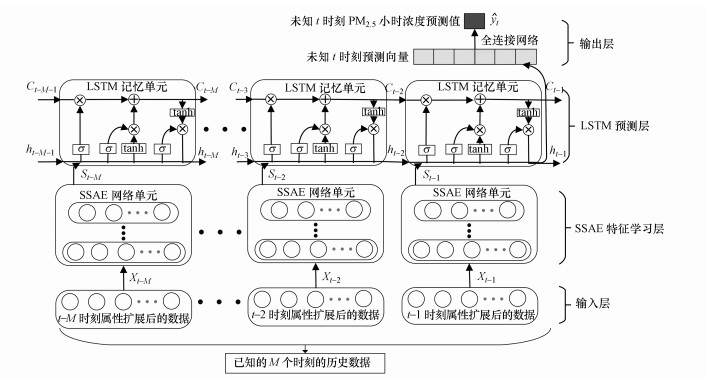 |
| 图 1 SSAE-LSTM模型结构 Fig. 1 Architecture of SSAE-LSTM neural network |
① 输入数据层:选择PM2.5的多种影响特征, 对PM2.5原始数据序列进行属性扩展, 并按照时间先后顺序将已知的M个历史时刻的扩展序列(Xt-M, …, Xt-2, Xt-1)输入到SSAE特征学习层中.
② SSAE特征学习层:采用SSAE网络单元对扩展序列(Xt-M, …, Xt-2, Xt-1)中各个时刻的数据进行低维抽象特征提取, 得到特征序列(St-M, …, St-2, St-1).
③ LSTM预测层:按照时间先后顺序将SSAE网络单元提取的抽象特征(St-M, …, St-2, St-1)输入到LSTM记忆单元中, 得到未知的t时刻的预测向量.
④ 输出层:以多层全连接神经网络的方式对LSTM模型输出的预测向量进行整合和降维, 输出未知的t时刻的PM2.5小时浓度预测值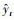
PM2.5颗粒物成分复杂, 其数值除了在时间和空间上表现出变化规律外, 还受到气象因素和空气污染物等多方面因素的影响.黄晓虎等(2017)研究表明, PM2.5与PM10、SO2、NO2、CO、O3具有较强的相关性.周曙东等(2017)和梅波等(2018)研究表明, PM2.5与温度、风速、降雨等因素呈负相关关系, 与相对湿度呈正相关关系, 且PM2.5受风向影响较大.马晓倩等(2016)和温佳薇等(2018)研究表明, PM2.5浓度在年、季度、月度、日内小时等不同时间尺度上具有不同的时间变化规律.不同空气监测站点由于所处城市不同(黄婕, 2018), 与渤海湾的相对位置不同(Yan et al., 2018), 因而具有不同的PM2.5分布特征.
已有研究表明, 京津冀地区空气监测站点的空气质量浓度与空间上邻近站点的空气质量浓度有较强的相关性(Wen et al., 2019).本文以京津冀城市群71个空气监测站点为研究对象, 通过Pearson相关系数分析空气监测站点与邻域站点PM2.5的相关性, 并选择最合适的邻域站点个数.站点与邻近k(1~70)个站点的平均Pearson相关系数如图 2所示, 可以看出, 随着邻近站点个数k的增大, 平均相关系数逐渐减小.由于邻域站点数量过多会增加后续预测模型的计算量, 当邻域站点数量k=6时, 不同年份的相关系数均在0.85左右, 表现出强相关性, 故本文选择最合适的邻域站点数量为6.
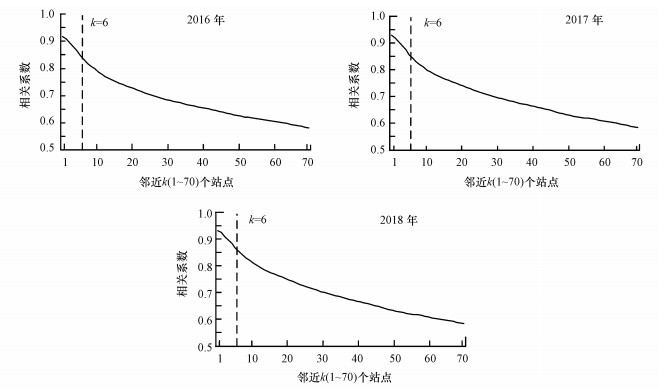 |
| 图 2 京津冀空气监测站点与邻近k个站点的平均相关系数 Fig. 2 Average correlation coefficient between Beijing-Tianjin-Hebei air monitoring station and neighboring k stations |
本文选取上述各个影响因素为PM2.5的影响特征, 对PM2.5原始序列进行属性扩展.对于任一站点si, 令X=(X1, X2, …, Xt, …, Xn)表示站点si经属性扩展后的时间序列, 其中, Xt包含站点si在t时刻的空气污染物变量、气象变量、时间特征变量和空间特征变量的小时值, 共96维.具体如下:
① 空气污染物变量:站点位置处及距离站点最邻近的6个站点的PM2.5、PM10、SO2、NO2、O3、CO小时浓度值和24 h浓度均值, 共84个变量.
② 气象变量:站点位置处的气温、相对湿度、降雨量、风速和风向数据, 共5个变量.
③ 时间特征变量:年份、季节、月份、日内小时时刻, 共4个变量.
④ 空间特征变量:站点编号、站点所在的城市、站点相对于渤海湾的位置(渤海湾以南或渤海湾以北), 共3个变量.
2.2 SSAE特征学习层SSAE特征学习层以经过属性扩展后的数据为输入, 采用无监督方法提取输入数据的抽象特征, 实现特征的压缩和降维.
SSAE由多个稀疏自编码器(Sparse Auto-Encoder, SAE)堆叠而成.SAE是一种对称的3层神经网络, 分为输入层、隐含层和输出层, 包含编码、解码两个阶段.令输入向量为Xt, 在编码阶段, 通过式(1)将Xt映射到低维隐含层ht.在解码阶段, 通过式(2)将ht映射到输出层, 得到Xt的重构向量

|
(1) |
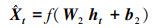
|
(2) |
其中, f(·)是激活函数, 本文采用Relu激活函数, W1、W2和b1、b2分别表示编码层和解码层的权重矩阵和偏置向量.
自编码器的训练目标为尽可能减少输入向量Xt和输出向量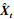
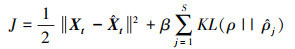
|
(3) |
式中, 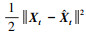
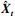

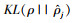
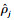
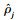
多个稀疏自编码器(SAE)堆叠组成栈式稀疏自编码器(SSAE), SSAE结构如图 3所示.SSAE中, 首先将输入数据Xt输入第一个SAE, 得到隐含层向量ht1, ht1为Xt的低维特征表示;接着将ht1输入第二个SAE, 得到隐含层向量ht2, ht2为ht1的低维特征表示;以此类推, 得到最后一个SAE的隐含层向量htN, 作为SSAE从输入数据Xt中学习到低维抽象特征.
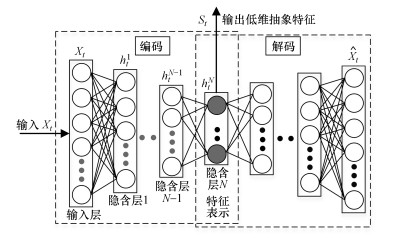 |
| 图 3 SSAE网络单元结构 Fig. 3 Architecture of SSAE neural network |
以上是SSAE特征学习层的公式化计算过程, 其中, 输入数据Xt为t时刻经属性扩展后的数据, 包含多种PM2.5影响特征.将SSAE特征学习过程作用于Xt, 可自动提取PM2.5的低维抽象影响特征, SSAE特征学习的流程图如图 4所示.
 |
| 图 4 SSAE特征学习层流程图 Fig. 4 Flowchart of SSAE feature learning layer |
基于LSTM的优良特性, 本文在SSAE-LSTM模型中加入LSTM预测层建立PM2.5时序预测模型.LSTM预测层以经SSAE特征学习后的M个时刻的低维抽象特征为输入, 学习历史数据中存在的长期依赖性, 输出下一时刻的预测向量.
LSTM预测层由多个LSTM记忆单元组成, 单元结构如图 5所示, 该单元主要遗忘门、输入门和输出门控制, 在任一t时刻的工作机制如下.
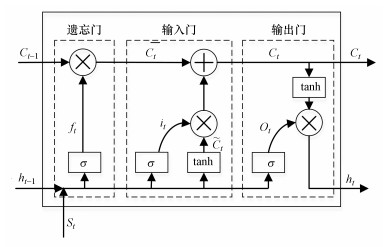 |
| 图 5 LSTM单元结构 Fig. 5 Architecture of LSTM neural network |
首先, 遗忘门结合t时刻LSTM网络的输入向量St和t-1时刻LSTM网络的预测向量ht-1计算衰减系数ft, 将t-1时刻LSTM网络的记忆单元Ct-1乘上衰减系数ft, 遗忘上一时刻记忆单元中无用的历史信息, 得到遗忘后的记忆单元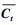
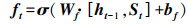
|
(4) |
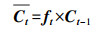
|
(5) |
接着, 输入门结合St和ht-1对记忆单元
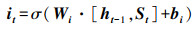
|
(6) |
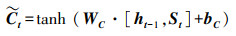
|
(7) |
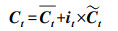
|
(8) |
最后, 输出门结合ht-1, St, Ct, 输出预测向量ht:
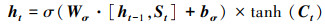
|
(9) |
式中, σ为sigmoid函数, tanh为tanh激活函数, Wf、Wi、WC、Wσ和bf、bi、bC、bσ分别表示权重矩阵和偏置向量.
以上是LSTM预测层的公式化计算过程.由相关研究可知, PM2.5有显著的自相关性.通过对已有PM2.5数据进行统计分析发现, 当前时刻的PM2.5浓度值不仅与距离该时刻最近6个时刻的历史数据有较强的相关性, 且与距离该时刻24 h的时刻的历史数据也有较强相关性.故本文将LSTM预测层的输入时间序列步长M设置为7, 以经SSAE特征学习后的t-24、t-6、t-5、t-4、t-3、t-2、t-1等7个时刻的低维抽象影响特征作为LSTM预测层的输入数据, 输出t时刻的PM2.5预测向量.LSTM预测层的流程图如图 6所示.
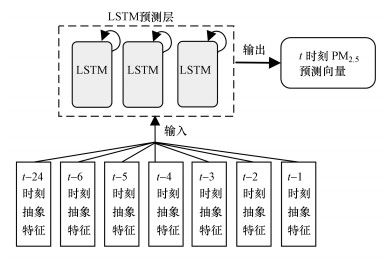 |
| 图 6 LSTM预测层流程图 Fig. 6 Flowchart of LSTM prediction layer |
2.2节、2.3节介绍的SSAE特征学习层和LSTM预测层已完成了SSAE-LSTM预测模型中最重要的特征提取过程和时序预测过程.SSAE-LSTM模型的最后一部分为全连接网络组成的输出层, 该层以LSTM预测层输出的预测向量为输入, 通过全连接网络的非线性映射功能对预测向量进行整合和降维, 输出下一时刻的PM2.5小时浓度预测值.输出层中, 网络节点的计算公式为:

|
(10) |
式中, xjk为第k层的节点j的值, wij为第k-1层的节点i到第k层的节点j的连接权值, Sk-1为第k-1层的节点个数, f(·)为激活函数, 本文采用Relu激活函数, bk为偏置.
3 数据来源与数据预处理(Data sources and preprocessing methods) 3.1 数据来源本文以空气污染较严重的京津冀城市群(姜磊等, 2018)为研究区域, 实验数据包括两类:地面空气监测站点的空气质量数据及气象数据.
空气质量数据来自于全国城市空气质量实时发布平台, 考虑到数据缺失问题, 本文选取了2016年1月1日—2018年12月31日期间京津冀城市群71个空气监测站点的空气质量数据, 数据更新频率为1次·h-1, 每条数据包括PM2.5、PM10、SO2、NO2、O3、CO在当前时刻的小时浓度和此前24 h的浓度均值.研究区域与空气监测站点的位置分布如图 7所示.
 |
| 图 7 研究区域与空气监测站点分布图 Fig. 7 Map of study area and atmospheric monitoring stations |
气象数据来自与环境云官方网站提供的空气质量指数(API), 本文获取了2016年1月1日—2018年12月31日期间京津冀城市群71个空气监测站点所在城市城区的气象数据, 数据更新频率为1次·h-1, 每条数据包括当前时刻的气温、相对湿度、降雨量、风向、风速等5个指标.
3.2 数据预处理本文数据预处理主要包括数据的缺失值处理、异常值处理、特征化和量纲归一化处理.
3.2.1 数据缺失值处理在现实生活中, 由于仪器故障、网络传输不稳定等不可控因素, 监测仪器会出现数据漏采的情况, 且服务器故障或停电也会造成网上平台发布数据缺失.本文统计了京津冀城市群71个空气监测站点各个空气变量的缺失率, 结果表明, PM10变量缺失率为12.80%, 其余各空气变量的缺失率在5%左右;统计了不同气象变量的缺失率, 结果表明, 温度、湿度、降雨量和风速变量的缺失率相同, 均为11.8%, 风向的缺失率为14.7%.
缺失数据会导致时间序列的周期性发生错位, 故不能直接采用删除法和简单填补法处理缺失值.本文根据数据特点, 选用线性插值法对缺失值进行填充, 公式如下:
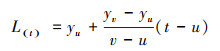
|
(11) |
式中, t为缺失值的时间节点, u和v分别为t时刻前和t时刻后未缺失数据的时间节点;yu、yv为u、v时刻的监测值;L(t)表示计算结果, 即插补值.
线性插值法适合于处理缺失率较低或者连续缺失时间较短的数据集.对于空气质量数据, 本文以7%为缺失率的阈值, 以6为连续缺失时间的阈值, 采用线性插值法对71个站点的空气变量进行缺失值处理, 处理流程如图 8所示.对于气象数据, 本文采用线性插值法对气象数据中的数值型变量进行补齐, 采用邻近补齐法对气象数据中的文本型变量-风向变量进行修复, 即用缺失值邻近时刻的未缺失数据填充缺失值, 处理流程如图 9所示.对于未填补的缺失值, 在后续预测时赋值为0.
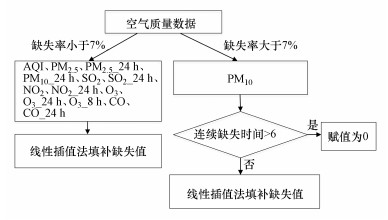 |
| 图 8 空气质量数据缺失值处理流程图 Fig. 8 Flow chart of missing value processing of air quality data |
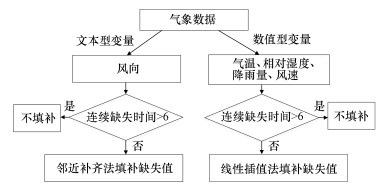 |
| 图 9 气象数据缺失值处理流程 Fig. 9 Flow chart of missing data processing of meteorological data |
经分析发现, PM2.5数据中的异常值主要是异常低值, 表现为在一段较平稳序列中突然出现一个数值较小的异常值, 且该异常值明显低于附近值.由于数据量较多, 人工识别此类异常值费时费力, 故本文提出基于集成经验模态分解的PM2.5异常低值检测与校正方法, 处理PM2.5异常低值.方法首先利用集成经验模态分解法(Ensemble Empirical Mode Decomposition, EEMD)(Wu et al., 2009; Wei et al., 2018)将PM2.5原始序列分解成不同频率的本征模态函数(IMF)和残余项, 然后利用低频IMF分量和残余项重构原始序列的整体趋势, 最后计算偏差比率, 检测和校正PM2.5异常低值.
令PM2.5原始时间序列为X=(x1, …, xt, …, xn), xt表示t时刻的PM2.5小时浓度值, 基于EEMD的PM2.5异常低值检测与校正的主要步骤如下:
步骤1:应用EEMD法将PM2.5原始时间序列X分解为一系列不同频率的IMF和一个残余项.
步骤2:把分解得到的低频IMF和残余项对应相加, 并减去白噪声, 得到PM2.5原始序列的趋势序列T=tend1, …, tendt, …, tendn.
步骤3:计算原始序列与趋势序列在各个时刻的偏差比率dratio(t), t时刻的偏差比率为:
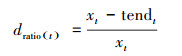
|
(12) |
步骤4:设置偏差比率的阈值, 将偏差比率大于阈值的数据识别为异常低值.
步骤5:对于识别出的异常值, 用相应位置的趋势数据进行替换, 从而实现异常值校正.
以图 10a中北京1001A站点在2017年3月21—30日期间的PM2.5原始数据为例, 采用基于EEMD的异常低值检测与校正方法对其进行异常低值处理, 处理过程如下:①设置参数:经多次实验后将白噪声振幅设为原始数据标准差的0.1倍, 噪声添加次数为5, IMF个数为11, 偏差比率阈值设为10;②采用EEMD对原始数据进行分解, 重构数据的整体趋势, 趋势数据如图 10b所示;③计算偏差比率, 检测异常低值, 并用趋势数据替换相应位置异常值, 实现PM2.5异常低值校正, 校正后的数据如图 10c所示.
 |
| 图 10 PM2.5异常低值处理实例 Fig. 10 Examples of processing abnormally low value in PM2.5 data |
神经网络不能理解文本型的数据, 所以需对文本型变量进行特征化处理.本文将年、季节、月、日内小时时刻等时间特征变量分别用1-3、1-4、1-12、1-24表示;将风向、站点所在的城市等文本变量, 用1, 2, …, n等自然数表示;对于站点相对于渤海湾的位置变量, 分别用1和2代表渤海以北和渤海以南.经特征化处理后, 所有变量均为数值型变量, 由于各变量衡量指标不同, 数据范围不同, 容易导致网络表达能力下降, 所以需对变量进行量纲归一化处理.本文采取max-min归一化方法将各个数值型变量放缩到0~1范围内:
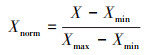
|
(13) |
式中, X为变量原始值, Xmax、Xmin分别为X的最大和最小值, Xnorm为X归一化后的值.
4 模型建立(Model building) 4.1 模型架构本文提出的SSAE-LSTM模型可用于PM2.5浓度的在线预测.为验证方法有效性, 本文以京津冀城市群71个监测站点为例, 建立融合SSAE-LSTM的PM2.5小时浓度预测模型, 预测过程可分为离线训练和在线预测两个模块, 流程如图 11所示.
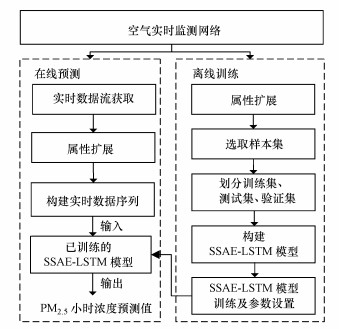 |
| 图 11 基于SSAE-LSTM模型的PM2.5预测流程 Fig. 11 Flowchart of PM2.5 prediction using SSAE-LSTM |
本文以京津冀区域71个空气监测站点为例, 从历史数据中提取样本集, 训练SSAE-SLTM模型, 训练过程主要包括以下5个步骤.
4.2.1 属性扩展选取2.1节所述的各个影响因素, 对京津冀地区71个站点的空气污染数据进行属性扩展.对于任一站点, 在2016年1月1日—2018年12月31日期间内共获取26304条小时数据, 组成的时间序列为X=(X1, X2, …, Xt, …, X26304), Xt包含t时刻的空气污染物、气象要素、时间特征和空间特征等96项相关特征变量的小时值.
4.2.2 选取样本集按照时间顺序依次从每个站点的时间序列X中提取样本, 第t个样本结构为(Xt, Yt), Xt为距离t时刻最近的6个时刻和距离t时刻24 h的时刻的历史时序数据, Xt={Xt-24, Xt-6, …, Xt-1}, Yt为t时刻的PM2.5小时浓度值, 每个站点共提取26280个样本, 71个站点共提取186万多个样本.
4.2.3 划分训练集、测试集和验证集为了验证模型在不同季节的预测效果, 实验按季节划分训练集和测试集.本文综合考虑光照、温度等各种因素, 以3—5月为春季, 6—8月为夏季, 9—11月为秋季, 12—2月为冬季(张歌等, 2014).从每个站点中选取2018年4个季度最后15 d(春季:2018年5月17—31日, 夏季:2018年8月17—31日, 秋季:2018年11月16—30日, 冬季:2018年2月14—28日)的样本为测试集, 其余为训练集.另外, 本文采用Holdout验证法防止过拟合, 在训练集中随机抽取2%的样本构建验证集.
4.2.4 构建SSAE-LSTM模型由于神经网络中隐含层节点个数的选取迄今为止都没有一个固定的算法, 故本文根据经验和一般原则设计了4种不同网络结构的SSAE-LSTM模型.首先, 本文设计了4层的SSAE网络(ssae_1、ssae_2、ssae_3、ssae_4)、两层的LSTM网络(lstm_1、lstm_2)和两层的全连接网络(fc_1、fc_2), 然后将不同层数的SSAE网络和LSTM网络相组合, 共得到4种SSAE-LSTM模型.SSAE-LSTM模型中, 每一层的神经元数量如表 1所示, 表中数字代表对应网络层的神经元数量, none表示模型不具有该网络层.
| 表 1 4种SSAE-LSTM网络模型的具体结构 Table 1 Structure of four SSAE-LSTM neural network models |
采用71个站点的全部训练样本集训练SSAE-LSTM模型.由于SSAE-LSTM网络中存在大量隐含层节点和待训练的权值, 如果直接采用梯度下降法训练模型, 容易产生梯度弥散或梯度消失等问题, 导致网络无法收敛.为了解决上述问题, 本文将SSAE-LSTM模型的训练分为无监督学习的逐层预训练阶段和有监督学习的整体参数微调阶段.
逐层预训练阶段利用逐层贪婪学习方法训练同结构的SSAE网络, 对SSAE网络模型的参数进行初始化:首先以2.2节SAE的损失函数(式(3))作为目标函数训练SSAE网络中第一层编码器SAE1, 生成权重矩阵w1和隐含层向量h1;然后以h1作为第二层编码器SAE2的输入, 按照同样的方式进行训练, 生成权重矩阵w2和隐含层向量h2, 以此类推, 逐层训练后面各层SAE, 最后得到一组w1、w2、w3、w4……wn权重.
整体精调阶段:首先将训练得到的w1、w2、w3、w4……wn权重设为SSAE-LSTM模型中SSAE网络的初始参数, 然后计算预测数据与真实数据之间的预测误差作为网络收敛代价, 利用梯度下降法对SSAE-LSTM模型整体权值进行微调.设SSAE-LSTM每批次(batch)输出的PM2.5预测序列为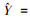


|
(14) |
逐层预训练阶段涉及到的参数包括:稀疏性约束项的权重(β)、稀疏性参数(ρ)、学习率(p_lr)、训练批次(p_ batch)和训练次数(p_epoch).整体微调阶段涉及的参数包括:时间步参数(M)、LSTM随机失活率(dropout)、学习率(f_lr)、训练批次(f_batch)和训练次数(f_epoch).其中, 对于时间步参数的设置, 本文已在2.3节做出了详细说明, 将时间步设置为7.对于其它参数, 本文采用网格搜索法进行实验, 最终确定的最佳参数如表 2所示.
| 表 2 SSAE-LSTM预测模型参数设置 Table 2 Parameter setting of SSAE-LSTM prediction model |
在线预测模块, 首先获取站点的实时数据流, 并对站点PM2.5原始序列进行属性扩展, 构建SSAE-LSTM模型的输入数据;然后将数据输入至训练好的SSAE-LSTM模型中;最后输出PM2.5小时浓度实时预测值.
本文以京津冀城市群71个空气监测站点为例, 假设离线训练模块提取的测试样本集的X部分为属性扩展后的数据, Y部分为下一时刻的PM2.5实测值.首先将测试样本集的X部分输入至训练好的SSAE-LSTM模型中, 得到预测结果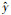

本文采用均方根误差RMSE、平均绝对误差MAE、一致性指数IA(黄婕, 2018)评价模型预测精度, 其中RMSE和MAE越小说明预测值和实测值在数值上的偏差越小, IA越接近1说明预测值与实测值的变化趋势和一致性程度越高, 公式如下:

|
(15) |

|
(16) |

|
(17) |
式中, N为样本个数, 
图 12展示了不同结构SSAE-LSTM模型在所有测试集上的预测精度, 可以看出, SSAE3-LSTM1模型在所有模型中表现最好, 主要体现在:模型的一致性指数IA最高, 模型均方根误差RMSE及平均绝对误差MAE最低.SSAE3-LSTM1模型IA指数高达0.99, 分别比SSAE3-LSTM2、SSAE4-LSTM1、SSAE4-LSTM2模型高0.03、0.01、0.02;RMSE值降到了13.98, 分别比SSAE3-LSTM2、SSAE4-LSTM1、SSAE4-LSTM2模型低8.75、0.12、3.66;MAE降到了7.90, 分别比SSAE3-LSTM2、SSAE4-LSTM1、SSAE4-LSTM2模型低9.80、0.60、3.87;说明三层SSAE编码器和一层LSTM网络的SSAE3-LSTM1网络更适合预测PM2.5小时浓度, 且具有较高的预测精度.这主要是因为在神经网络模型中, 若模型的网络层数过少, 容易导致模型学习能力弱, 容错性差;而模型的网络层数过高则容易产生过拟合, 不仅增加学习时间, 而且降低了模型的泛化能力;故网络层数适中的SSAE3-LSTM1模型具有较稳定的预测性能和较强的鲁棒性.
 |
| 图 12 4种SSAE-LSTM预测模型在所有测试集上的预测性能评价对比 Fig. 12 Comparison of four SSAE-LSTM prediction model for predicting performance evaluation on all test sets |
为了证明本文提出的SSAE编码器的有效性, 实验设计了多变量LSTM预报模型, 模型相比SSAE3-LSTM1仅缺少SSAE特征学习层, 且输入数据与SSAE3-LSTM1相同.为了证明空气污染物、气象要素、时间特征和空间特征等预测特征的重要性, 实验设计了单变量LSTM模型, 模型结构与SSAE3-LSTM1中的LSTM预测层相同, 模型输入为PM2.5历史数据.此外, 本文还与经典的随机森林回归(RFR)进行了对比实验, 实验中RFR的决策子树个数设为50, 特征子集的最大特征个数为特征总数的开方, 内部节点再划分所需最小样本数为30.
图 13展示了SSAE3-LSTM1及对比模型在71个站点的所有测试集上的预测精度.从图中可以看出, 相比于其它3种算法, SSAE-LSTM模型在全部测试集上的预测精度最高:①SSAE3-LSTM1模型的RMSE、MAE、IA值分别比去除了SSAE特征学习层的多变量LSTM模型低0.62、低0.99、高0.1, 说明在相同的数据训练下, 在预测模型中加入SSAE特征学习层可以有效地学习PM2.5的抽象影响特征, 提高模型的预测精度;②SSAE3-LSTM1模型的RMSE、MAE、IA值分别比未经属性扩展的单变量LSTM模型低0.51、低1.14、高0.2, 说明在预测模型中充分考虑PM2.5的多种影响特征可以有效地降低预测误差;③SSAE3-LSTM1模型的RMSE、MAE、IA值分别比RFR模型低1.16、低1.31、高0.2, 说明相较于传统预测模型, 本文提出的SSAE3-LSTM1模型能够更好地预测PM2.5小时浓度.
 |
| 图 13 SSAE3-LSTM1及其它预测模型在所有测试集上的预测性能评价对比 Fig. 13 Comparison of SSAE3-LSTM1 and other prediction models for predicting performance evaluation on all test sets |
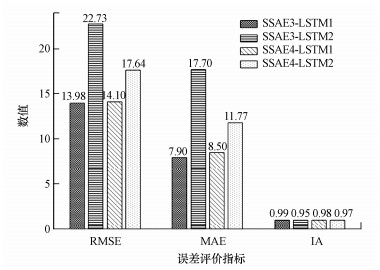
图 14分别列出了SSAE3-LSTM1及对比模型在71个站点的春、夏、秋、冬不同季节测试集上的预测精度.总体来看, 4个预测模型在测试集上的RMSE和MAE精度都表现出夏>春>秋>冬的特点, 而一致性指数IA表现出秋>冬>夏>春的特点.从不同评价指标的精度大小来看, SSAE3-LSTM1模型在4个季节上的IA值均高于其它模型, RMSE和MAE值均低于其它模型, 说明相比其它模型, 本文提出SSAE3-LSTM1预测模型能够更加精确地预测不同季节的PM2.5小时浓度值.
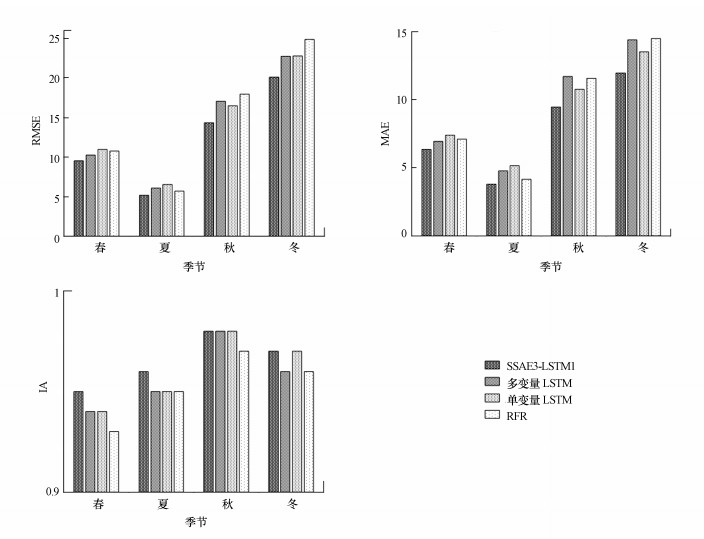 |
| 图 14 SSAE3-LSTM1及其它模型在不同季节测试集上的预测性能评价对比 Fig. 14 Comparison of SSAE3-LSTM1 and other prediction models for predicting performance evaluation on different season test sets |
综上所述, SSAE-LSTM模型预测性能要优于未加SSAE特征学习层的多变量LSTM模型、未考虑PM2.5多种影响因素的单变量LSTM模型及传统的RFR模型.
5.4 不同季节下SSAE-LSTM模型的适用性分析为更加全面评价模型性能, 将SSAE3-LSTM1模型在71个空气监测站点的不同季节测试集上的预测值和实测值绘制如图 15所示的散点图, 分析SSAE3-LSTM1模型在不同季节的适用性.图 15中, 横坐标表示实测值, 纵坐标表示预测值, 趋势线表示预测值和实测值的回归线, R2表示决定系数, R2越接近于1表示预测值和实测值的线性关系越强.从图 15中可以看出, 春、夏、秋、冬4个季节测试集的预测值和实测值的R2分别为0.86、0.92、0.96、0.93, R2接近于1, 说明训练得到的SSAE3-LSTM1模型可以同时对71站点进行预测, 且对各个站点不同季节的预测结果均接近于真实值.
 |
| 图 15 SSAE3-LSTM1模型在71个站点不同季节测试集上的预测值和实测值散点图 Fig. 15 Scatter plots of the predicted and measured values of the SSAE3-LSTM1 model on different season test sets at 71 stations |
北京市万寿西宫空气监测站点位于城市核心区, 空气污染较严重.本文以万寿西宫站点为例, 进一步验证模型在不同季节下的适用性.图 16展示了SSAE3-LSTM1模型在万寿西宫站点的不同季节测试集上的预测结果, 可以看出, 在空气质量较好的夏季, 模型具有最高的RMSE和MAE精度, 分别为4.74、3.36, 预测值和实测值的数值偏差较小;在空气质量次之的春季, 模型的RMSE和MAE精度分别为10.80、6.90, IA指标为0.97, 预测精度较高;在空气质量最差的秋、冬季, 模型的一致性指数高达0.99, 预测值与真实值的趋势基本相同, 特别是对于“PM2.5浓度峰值”位置也具有较好的预测效果.万寿西宫站点的预测结果证明SSAE3-LSTM1模型可以适应不同季节下的预测需求, 不仅可以用于空气质量较好的天气的PM2.5浓度预报, 而且可以用于重度污染天气的PM2.5浓度预警, 以避免更加严重的空气污染事件发生.
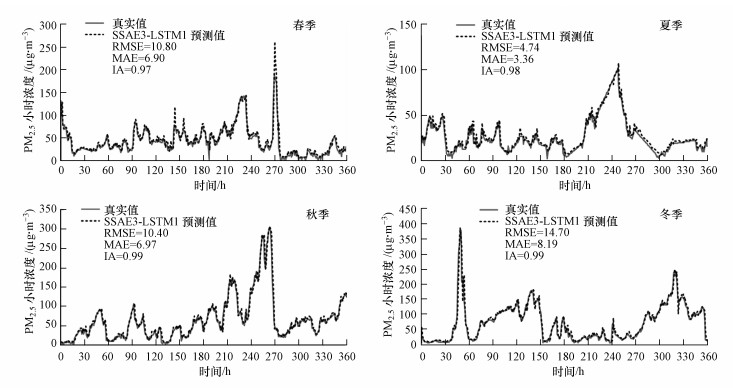 |
| 图 16 SSAE3-LSTM1模型在万寿西宫站点不同季节测试集上的预测结果 Fig. 16 Prediction results of SSAE3-LSTM1 model on different season test sets of Wanshou Xigong Station |
综上所述, 将SSAE编码器和LSTM网络相结合可实现不同季节和不同天气质量情况下的PM2.5小时浓度准确预测, 证明SSAE-LSTM模型具有应用上的可行性和可靠性.此外, SSAE-LSTM模型可作为多输出预测模型, 首先计算未来第1个时刻的预测值, 然后基于第1个时刻的预测值来计算未来第2个时刻的预测值, 以此类推, 实现多步的PM2.5小时浓度预测.但在进行多步预测时, 须将得到的预测值作为实测值加入到接下来的预测过程中, 由于预测值中包含一定的误差, 因此, 容易产生误差累积的问题, 且随着预测步长增大, 累积的误差越大.如何减少累计误差、提高PM2.5小时浓度多步预测的精度, 是未来利用SSAE-LSTM模型进行多步PM2.5小时浓度预测时需要解决的关键问题.
6 结论(Conclusions)1) 本文构建了数据预处理方法, 提高了样本数据质量.同时, 采用线性插值法处理空气质量数据中的缺失值, 分别采用线性插值法和邻近补齐法处理气象数据中数值型变量和文本型变量的缺失值, 提出基于集成经验模态分解(EEMD)的PM2.5异常低值检测与校正方法处理PM2.5数据中的异常低值.
2) 本文提出了融合SSAE编码器和LSTM网络的PM2.5小时浓度预测模型SSAE-LSTM.首先分析了PM2.5的影响因素, 将模型的输入数据扩展为具有PM2.5时空特征、空气污染物、气象因素等96维变量的时间序列;然后采用SSAE编码器从输入数据中自动学习PM2.5的低维抽象特征;最后结合LSTM网络建立时序预测模型, 对京津冀城市群71个站点的PM2.5浓度进行协同训练与预测.本文共构建了4种不同结构的SSAE-LSTM模型, 结果表明, 3层SSAE编码器和1层LSTM网络的SSAE3-LSTM1模型的预测效果最好, 具有较稳定的预测性能和较强的鲁棒性.
3) 将SSAE3-LSTM1模型与多变量LSTM模型进行实验对比, 证明本文提出的SSAE编码器可以有效地从多种PM2.5影响特征中自动学习抽象特征, 提高预测精度;与单变量LSTM模型对比, 证明在预测模型中充分考虑PM2.5的多种影响特征可以提高模型的预测性能;与RFR模型对比, 证明本文提出的SSAE3-LSTM1模型具有比传统预测模型更好的预测效果.
4) 分析了SSAE3-LSTM1模型在京津冀城市群71个站点不同季节测试集上的预测值和实测值, 结果表明, SSAE3-LSTM1模型可以适应不同季节下的PM2.5小时浓度预测需求.同时, 分析了SSAE3-LSTM1模型在北京市万寿西宫站点上的预测值和实测值, 表明SSAE3-LSTM1模型可以用于不同空气质量情况下的PM2.5小时浓度预报.
Bai Y, Zeng B, Li C, et al. 2019. An ensemble long short-term memory neural network for hourly PM2.5 concentration forecasting[J]. Chemosphere, 222: 286-294. DOI:10.1016/j.chemosphere.2019.01.121 |
郭晓雷. 2011. 城市空气质量预报方法研究综述[J]. 科技传播, 2011(15): 50-55. |
Gnouma M, Ladjailia A, Ejbali R, et al. 2019. Stacked sparse autoencoder and history of binary motion image for human activity recognition[J]. Multimedia Tools and Applications, 78(2): 2157-2179. DOI:10.1007/s11042-018-6273-1 |
黄婕.2018.基于RNN-CNN集成深度学习模型的PM2.5小时浓度预测研究[D].杭州: 浙江大学 http://cdmd.cnki.com.cn/Article/CDMD-10335-1018259850.htm
|
黄晓虎, 韩秀秀, 李帅东, 等. 2017. 城市主要大气污染物时空分布特征及其相关性[J]. 环境科学研究, 30(7): 1001-1011. |
Hinton G, Deng L, Yu D, et al. 2012. Deep neural networks for acoustic modeling in speech recognition:The shared views of four research groups[J]. IEEE Signal Processing Magazine, 29(6): 82-97. DOI:10.1109/MSP.2012.2205597 |
姜磊, 周海峰, 赖志柱, 等. 2018. 中国城市PM2.5时空动态变化特征分析:2015-2017年[J]. 环境科学学报, 38(10): 3816-3825. |
Jia W, Muhammad K, Wang S, et al. 2019. Five-category classification of pathological brain images based on deep stacked sparse autoencoder[J]. Multimedia Tools and Applications, 78(4): 4045-4064. DOI:10.1007/s11042-017-5174-z |
Li X, Peng L, Yao X, et al. 2017. Long short-term memory neural network for air pollutant concentration predictions:Method development and evaluation[J]. Environmental Pollution, 231: 997-1004. DOI:10.1016/j.envpol.2017.08.114 |
马晓倩, 刘征, 赵旭阳, 等. 2016. 京津冀雾霾时空分布特征及其相关性研究[J]. 地域研究与开发, 35(2): 134-138. |
梅波, 田茂再. 2018. 基于时空模型北京市PM2.5浓度影响因素研究[J]. 数理统计与管理, 37(4): 571-586. |
Mandi M, Genc V M I. 2018. Post-fault prediction of transient instabilities using stacked sparse autoencoder[J]. Electric Power Systems Research, 164: 243-252. DOI:10.1016/j.epsr.2018.08.009 |
孙宝磊, 孙暠, 张朝能, 等. 2017. 基于BP神经网络的大气污染物浓度预测[J]. 环境科学学报, 37(5): 1864-1871. |
王秦, 李湉湉, 陈晨, 等. 2013. 我国雾霾天气PM2.5污染特征及其对人群健康的影响[J]. 中华医学杂志, 93(4): 2691-2694. |
温佳薇, 贺军亮, 赵晴, 等. 2018. 京津冀地区PM2.5的时空效应研究[J]. 环境污染与防治, 40(9): 1033-1038. |
Wen C, Liu S, Yao X, et al. 2019. A novel spatiotemporal convolutional long short-term neural network for air pollution prediction[J]. Science of the Total Environment, 654: 1091-1099. DOI:10.1016/j.scitotenv.2018.11.086 |
Wu Z, Huang N E. 2009. Ensemble empirical mode decomposition:A Noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 1(1): 1-41. |
Wei F, Wang S, Fu B, et al. 2018. Vegetation dynamic trends and the main drivers detected using the ensemble empirical mode decomposition method in East Africa[J]. Land degradation & development, 29(8): 2542-2553. |
尹建光, 彭飞, 谢连科, 等. 2018. 基于小波分解与自适应多级残差修正的最小二乘支持向量回归预测模型的PM2.5浓度预测[J]. 环境科学学报, 38(5): 405-413. |
Yan D, Lei Y, Shi Y, et al. 2018. Evolution of the spatiotemporal pattern of PM2.5 concentrations in China-A case study from the Beijing-Tianjin-Hebei region[J]. Atmospheric Environment, 183: 225-233. DOI:10.1016/j.atmosenv.2018.03.041 |
周曙东, 欧阳纬清, 葛继红. 2017. 京津冀PM2.5的主要影响因素及内在关系研究[J]. 中国人口·资源与环境, 27(4): 102-109. |
张歌, 陈义珍, 刘厚凤, 等. 2014. 北京地区灰霾污染特征[J]. 生态环境学报, 23(12): 1946-1952. |
Zhao J, Deng F, Cai Y, et al. 2019. Long short-term memory-Fully connected (LSTM-FC) neural network for PM2.5 concentration prediction[J]. Chemosphere, 220: 486-492. DOI:10.1016/j.chemosphere.2018.12.128 |
Zhang Y, Peng H. 2017. Sample reconstruction with deep autoencoder for one sample per person face recognition[J]. IET Computer Vision, 11(6): 471-478. DOI:10.1049/iet-cvi.2016.0322 |
 2020, Vol. 40
2020, Vol. 40


