环境科学学报  2019, Vol. 39 Issue (12): 4187-4195
引用本文
张凯, 赵天良, 曹乐, 等. 2019. 街道峡谷对近地层风场影响的观测和模拟分析[J]. 环境科学学报, 39(12): 4187-4195.
Zhang K, Zhao T L, Cao L, et al. Observation and simulation analyses on influence of street canyon on near-surface winds[J]. Acta Scientiae Circumstantiae, 39(12): 4187-4195.
街道峡谷对近地层风场影响的观测和模拟分析    [PDF全文]
张凯1, 赵天良1, 曹乐1, 胡小明2, 郑小波3, 杨清健1, 于超1    
1. 南京信息工程大学大气物理学院, 气象灾害教育部重点实验室, 气候与环境变化国际合作联合实验室, 气象灾害预报预警与评估协同创新中心, 中国气象局气溶胶与云降水重点开放实验室, 南京 210000;
2. 俄克拉荷马大学气象学院, 俄克拉荷马州 诺曼 73072;
3. 贵州省山地环境气候研究所, 贵阳 550000
收稿日期: 2019-04-01; 修回日期: 2019-05-08; 录用日期: 2019-05-08
基金项目: 国家重点研发计划试点专项项目(No.2016YFC0203304);国家自然科学基金(No.41830965, 91744209);江苏省研究生科研与实践创新计划项目(No.KYCX18_1027)
作者简介: 张凯(1994-), 男, E-mail:1443513495@qq.com
通讯作者（责任作者）: 赵天良, E-mail:tlzhao@nuist.edu.cn
摘要：城市街道峡谷结构对近地面边界层的风场环流等气象要素具有重要影响，可导致城市局地空气污染分布发生变化.随着城市化发展及城市空气质量变化，街道峡谷的城市空气污染影响日益突出，分析街道峡谷内部风场成为认识和治理我国城市空气污染的一条重要途径.鉴于目前我国鲜有城市街道尺度大气边界层精细气象观测研究，本文分析了美国俄克拉荷马大学的街道峡谷精细气象观测数据及其FLUENT模拟.结果表明：街道峡谷内风场结构变化依赖大气背景风向，当背景风向平行于街道峡谷走向时，街谷两岸风速几乎没有差异，而在背景风向垂直于街道峡谷走向时，由于高空风进入街谷形成的涡旋气流对街道峡谷风场有补充作用，峡谷两侧中层高度风场差异变大，风速差值大约为0.5 m·s-1，且街道峡谷两岸风速差异得到了FLUENT模式的验证，但模式对迎风岸的风速模拟存在高估，模拟的中层高度处两岸风速差值为1.6 m·s-1.观测资料分析揭示大气边界层稳定度条件对街道峡谷内风场分布也有很大影响，中性稳定条件下街道峡谷两岸近地层风速差异最大，输送进入峡谷空间的风速增量比原峡谷内风速大约高1倍，其它稳定度条件下街谷两岸风速差异被削弱.
关键词：街道峡谷    近地层风场    FLUENT    大气边界层稳定度    
Observation and simulation analyses on influence of street canyon on near-surface winds
ZHANG Kai1, ZHAO Tianliang1, CAO Le1, HU Xiaoming2, ZHENG Xiaobo3, YANG Qingjian1, YU Chao1    
1. Key Laboratory of Meteorological Disaster, Ministry of Education, Joint International Research Laboratory of Climate and Environment Change, Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Key Laboratory for Aerosol-Cloud-Precipitation of China Meteorological Administration, School of Atmospheric Physics, Nanjing University of Information Science & Technology, Nanjing 210000;
2. School of Meteorology, University of Oklahoma, Norman OK 73072;
3. Guizhou Institute of Mountainous Environment and Climate, Guiyang 550000
Received 1 April 2019; received in revised from 8 May 2019; accepted 8 May 2019
Abstract: The structures of urban street canyon play an important role in the near-surface meteorological elements such as wind field circulation, which can affect the distribution of urban air pollutants. With the development of urbanization and changes in atmospheric environmental quality, the impact of street canyons on urban air pollution has become increasingly prominent. Analyzing the structure of wind field inside street canyons has become an important way to understand and solve the problem of air pollution. In view of the lack of fine meteorological observation in the atmospheric boundary layer at urban street scale, this paper analyzes the fine observation data of the street canyon in the University of Oklahoma and conducts the FLUENT simulation. Results show that the distribution of the wind field within the street canyon is largely dependent on the atmospheric background wind direction. When the background wind direction is parallel to the street canyon, there is almost no difference in wind speed between the south and north sides of street canyon. While perpendicular, the difference of wind speed between two sides at mid-level height becomes the largest because of the supplement of vortex flow caused by the high-altitude wind entering the street canyon, the wind speed difference is about 0.5 m·s-1. The wind speed differences between two sides of the street canyon are verified by FLUENT. However, the modeling provides an overestimation of wind speed on the windward shore, the simulated mid-level difference is about 1.6 m·s-1. The stability of atmospheric boundary layer also has a great influence on the wind field by analyzing the observation data, the difference of wind speed between two sides of street canyon reach maximum under neutral conditions of stability in the near-surface layer. The increment of wind speed by delivery into the street canyon is about twice as high as the normal winds in the canyon. The differences in wind speed between the two sides of street canyon decline under other stability conditions.
Keywords: street canyon    near-surface layer wind    FLUENT    atmospheric boundary layer stability    
1 引言(Introduction)

街道峡谷可定义为由于城市中的建筑物群所分割而形成的类似于自然峡谷的结构, 目前定义的街道峡谷除了上述结构之外, 还包括由两处建筑物阻挡而形成的峡谷区域(Klein et al., 2015).由于建筑群的阻挡作用, 高空气流被切断, 峡谷内部形成涡旋结构, 且街道峡谷多种形态的几何形状和下垫面特征使得街道峡谷周围的流场、温度场和湍流场变得异常复杂(王乐等, 2012；徐伟嘉等, 2012).近年来, 随着城市高层建筑增加, 类似的结构在城市中逐渐变多, 并且街道峡谷是城市居民的主要活动区域之一, 内部的风场特性对汽车尾气及污染物等的扩散分布有着重要影响(幸鸿等, 2011；高海宁等, 2017), 污染物浓度在街道峡谷复杂地形的影响下进一步变化(Kwak et al., 2014), 进而影响城市居民健康.还有研究表明, 街道峡谷会加剧城市热岛效应, 峡谷内的温度可能会比外部高出2~4 ℃(Nunez et al., 1977).上述问题与城市高层建筑的数量、间距、位置等有着十分密切关系.目前, 在我国高层建筑不断增多的背景下, 城市规划中应充分考虑到“峡谷效应”带来的影响, 合理地对高层建筑进行规划, 并有意识地加大建筑物的间距, 留出风道, 减弱“峡谷效应”, 减轻城市污染带来的危害(王纪武等, 2012).

对于街道峡谷流场的研究始于20世纪60年代, Kennedy等(1977)的实测结果表明, 街道高宽比、街道峡谷几何结构及街道两侧建筑物屋顶风速对街道峡谷内部风场有很大影响；Depaul等(1986)对高宽比为1.4的街道峡谷内的风速进行了观测分析, 发现交通源产生的附加湍流是影响该地风场的重要因素；Oke(1988)根据高宽比对街道峡谷的类型进行了划分, 列举了不同高宽比条件下街道峡谷内出现的涡旋结构类型.此后, 一系列的观测活动、流体力学模式都被应用到街道峡谷中以探索这种特殊地形的流场分布.2003年俄克拉荷马城的“Joint Urban2003(JU 2003)”观测活动使学者们对街道峡谷内的流场特性及低层的湍流特征有了初步的了解(Nelson et al., 2015)；Klein等(2007)发现稳定度对街道峡谷内的流场有很大的影响, 其中, 湍流是一个重要的影响因素.观测活动虽然可以真实地获取某一地区特定时间段的气象场信息, 但数据受到仪器分布位置和观测持续时间的限制, 所能代表的时空范围非常有限, 而利用CFD建立研究对象的计算模型, 将流体动力学应用于模型上进行计算, 可以分析研究流体在该模型上的动力和热力活动, 从而实现对多种流体问题的数值模拟, 很好地弥补了观测活动的瑕疵.Walton等(2002a; 2002b)利用大涡模式模拟了街道峡谷中的湍流结构, 并与观测资料对比, 发现模拟结果与观测数据具有良好的一致性, 并结合湍流结构分析了污染物在街谷中的扩散机制；李磊等(2010)对北京郊区佛爷顶地面测站的周边区域进行了数值模拟试验, 通过与观测资料对比, 验证了FLUENT用于复杂地形风场模拟的可行性和准确性；Sabatino等(2008)使用FLUENT研究了污染物在高宽比为1的街谷中的扩散特性, 从他们的工作中可以发现FLUENT应用于街道峡谷风场模拟的可行性；刘建峰等(2017)则利用计算流体力学模式对街道峡谷内的风场特征及污染物的传输过程进行了模拟, 发现随着街道峡谷高宽比和建筑物间隔距离的变化会导致峡谷内的风场变化.

目前对于街道峡谷的构造及相应流场特征已经有了一些了解, 但关于街道峡谷内部空间的流场差异尚没有详细的研究说明；此外, 关于外部风场对街道峡谷内风场的贡献也没有具体的研究, 不同稳定度条件下街道峡谷内的流场特征也尚未研究透彻.城市街道峡谷结构会影响近地面边界层的风场环流等气象要素, 进而导致城市空气污染水平变化；同时, 城市街道峡谷的空气污染影响作用在城市化发展进程下日益突出, 分析城市街道峡谷结构内部风场成为认识和解决我国城市空气污染的重要手段之一.鉴于目前国内鲜有城市街道尺度大气边界层气象要素的精细观测, 本文分析了俄克拉荷马大学的精细气象观测资料, 并利用FLUENT模型对街道峡谷内的流场进行模拟, 通过对街道峡谷内部空间的风速差异和稳定度对街道峡谷两岸风速的影响进行分析, 以期有助于完善城市规划及进一步认识城市街道对空气污染的影响.

2 数据与方法(Data and methods) 2.1 研究区域

本文的研究区域为美国俄克拉荷马大学校园内两幢建筑楼所构成的峡谷空间(图 1), 该区域呈东西走向, 高宽比为0.27, 根据Oke(1988)及Zajic等(2015)对于街道峡谷类型的分类, 属于宽街谷类型, 可以作为个例来研究街道峡谷的流场特征.研究资料包括2009—2010年三维超声风速仪的部分观测数据, 仪器采样频率为10 Hz, 误差控制在0.05 m·s-1范围内, 可获取风向及各个方向的速度分量(u、v、w)信息.在整个峡谷区域分布有13个观测点, 本次分析主要选取E1、D1、E4、D3、E2、B2 6个位置的观测数据, 这6个样点分布在3根桅杆(B、D、E)上, 具体位置信息见图 2、表 1.此外, 本文还使用了位于研究区域北部5 km外中尺度观测点的理查森数(Ri)数据, 近似作为研究区域的稳定度数据, 通过Ri的大小划分稳定度, 将Ri < -1作为不稳定层结, Ri>1为稳定层结, -1≤Ri≤1为中性层结(盛裴轩, 2013；毕雪岩等, 2005).

图 1 研究区域概况 Fig. 1 Overview of research area

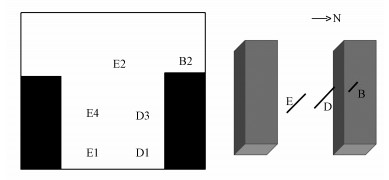图 2 本研究选取6个位置的仪器分布 Fig. 2 Instrument distribution at chosen six observation points

表 1 6个观测点位置信息 Table 1 Location information of six observation points
2.2 数据前处理

由于观测数据中包含的噪声数据可能会影响分析结果, 因此, 需要对观测数据进行质量控制.本文选用的方法遵循拉伊达准则, 以3倍测量列的标准偏差限为依据, 凡超过此界限的误差, 就认为不属于随机误差的范畴, 应当作为异常值被剔除, 即如果某测量值与平均值之差大于标准偏差的3倍, 则予以剔除(Shen et al., 2017).对于观测数据中的风速分量u、v、w则直接进行筛选剔除, 然后根据筛选后的u、v、w合成出风向和风速.除此以外, 若某一时刻u、v、w中的任意一个被剔除, 则该时刻的其他数据也作为异常值剔除.由于2010年6月的数据使用次数较多, 因此, 表 2展示了该月观测数据异常值数占样本总数的分布, 从表格数据来看, 观测数据的质量较高, 有利于增加分析结果的可信度.

表 2 2010年6月观测数据异常值分布 Table 2 Abnormal observation values in June 2010
2.3 模拟设置

本文使用美国Fluent公司开发的商业CFD软件FLUENT, 它可以模拟从不可压缩流体到高度可压缩流体的复杂流动问题, 采用多种求解方法和多重网格加速收敛技术, 能达到很好的收敛速度和求解精度, 目前被广泛应用于与流体力学相关的航天、水运、汽车制造、气象等各个行业.FLUENT通过以下步骤分析问题：①前处理：包括确定几何形状, 生成计算网格；②确定物理模型：包括求解方程的选择及流体特性的确定；③选择计算模型：包括选择解算器和设置边界条件；④决定求解过程：包括调节求解控制参数等；⑤后处理：采用多种方式显示和输出计算结果.

其中, 步骤④中的求解过程对于大气边界层内的空气流动而言主要是求解不可压缩流体的连续方程和动量守恒方程(唐家鹏, 2013)：

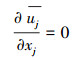
(1)
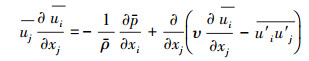
(2)

式中, i、j分别代表x方向和y方向；u为速度；ρ为密度；p为压力；ν为粘滞系数；u′为湍流脉动量.

将研究区域的街道峡谷空间设定在计算区域中心, 计算区域的大小设置为150 m×150 m×150 m, 而构成街道峡谷的两栋楼均设置为14 m×80 m×12 m的模型.利用ICEM-CFD软件, 设置一系列坐标点, 点成线, 线成面, 面成体, 然后进行块的分割, 分离出两栋楼构成的街道峡谷空间, 构造为需要的CAD模型；再通过格点的分配将整个计算区域划分为许多个网格, 网格数为50×50×15, 网格分辨率为3 m, 将网格文件输出, 并导入FLUENT软件中, 检查网格质量和设定的计算区域尺寸, 设置所需要的初始背景风(垂直于街谷走向3 m·s-1的水平风)及求解所需要的一系列参数(表 3), 经过FLUENT求解控制方程组得到计算区域内的风场, 最后通过后处理软件显示模拟结果.

表 3 FLUENT中各项参数设置 Table 3 Parameter setting in Fluent model
3 结果及讨论(Results and discussion) 3.1 背景风向对街道峡谷内风场的影响

通过筛选观测数据中背景风向分别为东、南、西、北的数据, 着重分析不同背景风对街道峡谷内风场的影响.图 3给出了不同背景风向条件下, 不同高度处街道峡谷内两岸的风速值(V=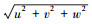)及南北岸的风速差值, 其中, 黑点为北岸风速, 银灰色星号为南岸风速, 黑色加号为南北风速插值绝对值的相反数.从图 3a、3d、3g、3j中可以看出, 15 m高度处由于位于街道峡谷以外, 在任何背景风向下, 街道峡谷南北两岸的风速几乎都没有差异.而在峡谷内部, 当背景风向为北风时, 从图 3b中可以看出9 m高度处南岸的风速值明显高于北岸, 南岸风速普遍比北岸高0.5 m·s-1左右, 而3 m高度处(图 3c)南、北岸风速则没有显著差异.在背景风向为南风的条件下, 图 3e给出了9 m高度处南、北岸的风速差异变化, 与北风条件下类似, 北岸的风速始终高于南岸, 差值大约为0.4 m·s-1, 3 m高度处(图 3f)有部分数据缺测, 但正常数据显示两岸同样不存在风速差异.当背景风向为东风时, 风沿着峡谷走向流动, 因此, 9 m(图 3h)和3 m(图 3i)处两岸的风速几乎一样.当背景风向为西风时, 南、北两岸的风速差理论上应该与东风的条件下一致, 但实际上3 m高度处的观测资料显示南岸的风速值高于北岸(图 3l), 结合当地的地形状况可以发现, 该区域西北角有树木的阻挡, 在西风条件下, 树木会阻挡西风进入街谷区域, 因此造成南岸风速高于北岸风速.综上所述, 街道峡谷内风场的空间分布依赖于背景风向, 当背景风垂直于峡谷走向时, 峡谷两岸出现明显的风速差, 且中层(9 m)的差异最为显著；而背景风平行于街道峡谷走向时, 综合来看街谷两岸不会出现明显的风速差异.

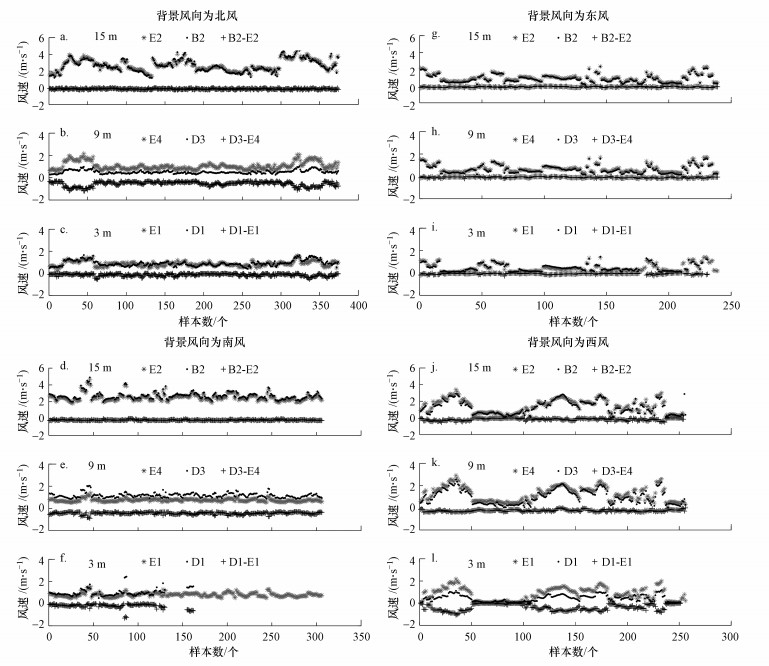图 3 不同背景风向下街道峡谷两岸风速差异 Fig. 3 Changes of wind speed under different background wind directions between two sides in the street canyon

已有研究表明, 当背景风垂直于街道峡谷走向时, 高空风会进入街谷区域, 并形成涡旋结构, 这将对街谷内的风场产生补充作用, 可能是造成街谷内两岸出现风速差的原因(蒋德海等, 2006；Zajic et al., 2015).图 4给出了不同大气背景风条件下, 9 m高度处风速垂直分量w的分布情况.从图中可以看出, 大气背景风向垂直于街谷走向时(图 4a、4b), 街谷两岸呈现出符号相反的w值, 北风(南风)条件下, 南岸E4处w值为负(正), 北岸D3处w值为正(负), 这可以证明街谷内垂直涡旋结构的出现.而在大气背景风向平行于街谷走向时(图 4c、4d), 两岸w值没有出现显著差异.

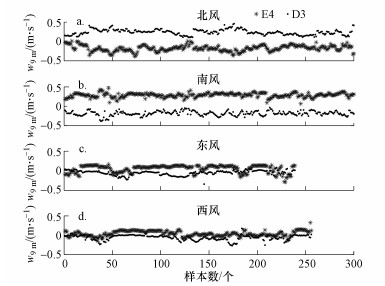图 4 不同大气背景风向下近地面9 m高度处风速垂直分量分布 Fig. 4 Distribution of vertical wind components at 9 m on near-surface layer under different background wind directions
3.2 FLUENT模拟结果

从3.1节结果可以发现, 背景风垂直于街道峡谷走向时, 街道峡谷内两岸的风速有显著的差异, 且两岸风速垂直分量w呈现相反的分布.因此, 本文利用FLUENT软件对大气背景风向垂直于街道峡谷走向时的风场进行了模拟及相关分析.

首先对FLUENT模式的模拟效果进行检验, 挑选出背景风为3 m·s-1的南风数据与模拟结果进行对比, 以9 m高度为例, 结果如图 5所示.在南风的影响下, 街谷内9 m高度北岸(D3)风速在0.8~1.4 m·s-1范围内波动, 南岸风速(E4)在0.5~0.9 m·s-1范围内变化(图 5a)；而模拟的9 m高度北岸(D3)风速为2.1 m·s-1, 南岸风速(E4)约为0.5 m·s-1(图 5b).由此可见, FLUENT模式对南岸风速的模拟效果较好, 对北岸风速有明显的高估.这可能是因为FLUENT模式没有考虑到实际下垫面的影响, 研究区域内的下垫面为草地, 还有一些低矮树木对内部风速有一定的影响.总体而言, FLUENT可以很好地呈现街谷内的风速差异.

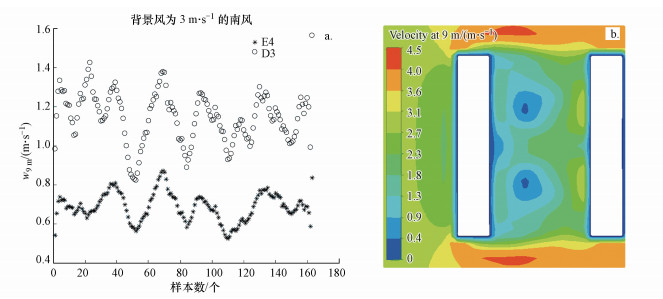图 5 近地面9 m高度处风速观测(a)与模拟结果(b)对比 Fig. 5 Comparisons between observation (a) and simulation (b) results at 9 m on near-surface layer

图 6给出了模拟的街谷垂直剖面(图 6a)和水平剖面(图 6b)的风场空间分布.从图 6a可以发现, 当背景风向垂直于街道峡谷走向, 即从A方向吹向B方向时, 高空风在经过街道峡谷时会在峡谷空间内形成一个涡旋结构, 且取不同的剖面时, 风场的空间分布略有差异.在图 6b中可以看出, 风从A方向来时, 遇到墙体A的阻挡将绕过建筑, 然后分别从墙B的两侧进入街道峡谷空间, 形成两个方向相反的涡旋结构, 且两个涡旋结构在街谷内呈对称分布(没有得到观测结果证实, 可能与周围建筑物的阻挡有关).这就解释了当背景风向垂直于街道峡谷走向时(3.1节中背景风向为北风或南风), 由于街道峡谷外的气流进入街道峡谷空间, 对内部的流场有补充作用, 使得B岸的风速高于A岸.

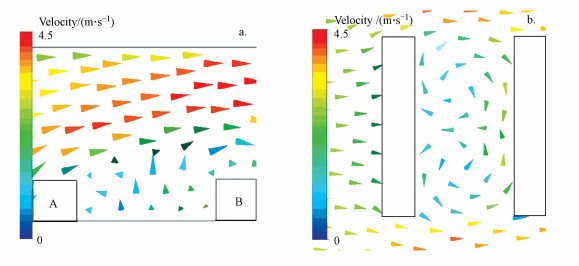图 6 街道峡谷模拟风场垂直剖面(a)和水平剖面(b) Fig. 6 Vertical (a) and horizontal (b) sections of the simulated wind field within the street canyon

图 7所示为3、9、15 m的风场模拟空间分布.从3 m高度的风场分布水平剖面图可以看出(图 7a), 垂直于街道峡谷走向的水平风绕过建筑物, 出现了上文所述的两种涡旋结构, 对街道峡谷内的风场有补充作用.而从图 7b的风速空间分布可以看出, FLUENT模拟的街道峡谷的两岸风速在3 m高度处存在差异, D1处的风速值(2.0 m·s-1)比E1处(0.8 m·s-1)大1.2 m·s-1.图 7c和图 7d分别给出了9 m高度处模拟的风向风速水平分布, 与3 m高度处的模拟结果基本一致, 街道峡谷内部两个涡旋结构仍然存在, 且D3处的风速值(2.1 m·s-1)比E4(0.5 m·s-1)高1.6 m·s-1.15 m处的风场模拟见图 7e、图 7f, 可以看出, 由于15 m高度已经超出了街道峡谷的空间(该处街道峡谷高度为12 m), 此处的涡旋结构和内部空间(3、9 m)并不一致, 从模拟的具体数值来看, B2(1.3 m·s-1)和E2(1.2 m·s-1)处的风速基本一致.综上可知, FLUENT模拟的风场空间分布与3.1节的观测结果基本一致, 模拟出的两岸风速差值略大于观测值, 15 m高度处风速几乎无差异, 9 m处的差异比较明显, 下风向岸风速比上风向岸风速高.导致这一现象的具体原因也可由FLUENT软件模拟的风场结果给出, 主要是由垂直方向的一个气流涡旋结构和水平方向的两个气流涡旋对街道峡谷内部风场的补充作用所形成的.而3 m高度处模拟结果与观测数据分析并不一致, 产生这一现象的原因由于观测资料的缺少还有待进一步研究.

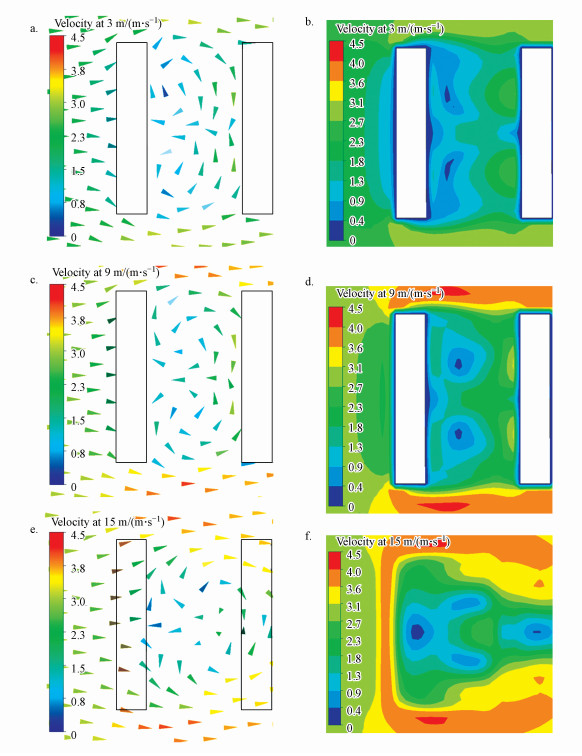图 7 3 m·s-1背景风条件下街道峡谷内3个高度处的风场 Fig. 7 Wind fields at three heights under 3 m·s-1 background wind in the street canyon

此外, 为了研究背景风垂直于街道峡谷走向时, 不同大小的背景风速对于街谷内风场的影响, 将输入的水平风速值增大至5 m·s-1并模拟街谷内风场的空间分布.从图 8中可以看出(以9 m高度的风场为例), 相对于3 m·s-1的模拟结果, 风速虽然增大(D3为2.4 m·s-1, E4为0.6 m·s-1), 但增大的趋势相对背景风速的增大是不明显的.由此可见, 街谷内两岸的风速差值会受背景风速的影响, 随着背景风速的增大, 街道峡谷内两岸风速差值会随之增大, 但增大的趋势不明显.

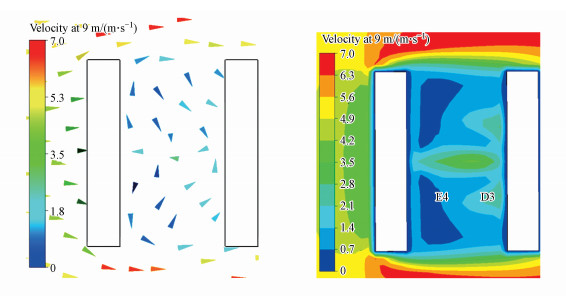图 8 5 m·s-1背景风条件下街道峡谷内9 m高度处的风场 Fig. 8 Wind field at 9 m under 5 m·s-1 background wind within the street canyon
3.3 稳定度对风场的影响

基于以上两部分的结论, 本文进一步讨论了背景风向垂直于街谷走向(南风或北风)的条件下, 不同稳定度对于街道峡谷3个高度风场的影响.当背景风向为北风时, 用街谷南岸风速减去北岸风速, 计算此差值与北岸风速的比值, 可以近似呈现出输送进入峡谷的风速增量占原来峡谷风速的权重(背景风向为南风时采用同样的处理方法).图 9的3张图分别代表稳定、不稳定、中性3种稳定度条件下街道峡谷内的风速差异(黑点代表 3 m高度, 黑色线代表 9 m高度, 黑色加号代表 15 m高度).在稳定条件下(图 9a), 位于街道峡谷上方的15 m处风场受稳定度的影响不大, 在9 m和3m位置处, 南、北岸的风速差异体现得比较明显, 输送进来的风速增量比峡谷中原有的风速大0.5~1.0倍.在不稳定条件下(图 9b), 南、北两岸的差异和稳定条件类似, 15 m处同样没有差异, 9 m高度处的差异最大, 平均约为0.5倍, 个别条件下差值所占权重可达1倍, 3 m高度处的两岸风速差异相对9 m高度略小.而在图 9c给出的中性条件下, 两岸的风速差值占峡谷内风速的比重达到了最大, 15 m高度不受峡谷地形的影响, 9 m高度处的权重值基本达到1, 部分甚至达到了2倍多, 3 m高度处差异较小, 但也基本达到0.5, 部分达到1左右.比较3种稳定度条件下的街道峡谷内两岸风速差异可以发现, 中性条件下街道峡谷结构对于风场的影响最为明显.可能是由于稳定条件下的大气层结结构限制了垂直方向的涡旋结构的形成, 从而导致对街谷内的风场补充较弱；而在不稳定条件下, 湍流旺盛, 湍流在峡谷内的混合作用使得两岸的风场差异缩小；但在中性条件下, 街道峡谷内没有任何机制可以阻止这种差异的产生, 因此, 可以很好地呈现街道峡谷内两岸的风速差异.

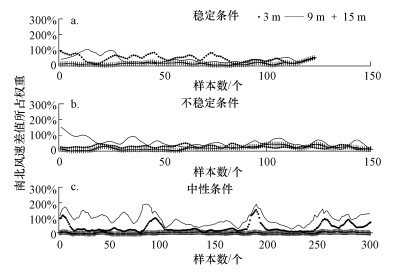图 9 不同稳定度条件下街道峡谷内两岸风速差异 Fig. 9 Difference of wind speed between two sides under different stabilities in the street canyon
4 结论(Conclusions)

1) 俄克拉荷马大学街道峡谷内风场的空间分布对风向有很强的依赖, 当背景风向垂直于街道峡谷走向时, 街谷两岸风速出现明显差异, 且中层高度最明显, 两岸风速差值约为0.5 m·s-1.背景风向平行于街道峡谷走向时, 几乎不存在差异.

2) FLUENT模式可以很好地呈现出街道峡谷内部的风场情况, 但对街谷内风速有一定的高估.模拟结果表明, 街道峡谷内部两岸风速差异是高空风进入街道峡谷形成的涡旋气流对内部风场的补充作用形成的, 外部风场的补充作用使得9 m高度处两岸风速差值达到1.6 m·s-1, 而当背景风速增大时, 两岸风速差异的变化不明显.

3) 大气边界层稳定度条件对街道峡谷内的风场分布也有很大影响, 中性稳定度条件下两岸风速差异最大, 输送进入峡谷空间的风速增量比原峡谷内风速大约高1倍, 其他两种稳定度条件下风速差异被削弱.

5 建议(Suggestions)

本文结论基于美国俄克拉荷马大学的近地面精细气象观测分析和模拟, 只是针对一种宽街谷类型的结果, 其他街谷类型的结果未来可以进一步开展研究.另外, 除了风场外, 温度场、浓度场等亦可未来开展研究.我国主要大气污染地区具有不同大气环流背景, 且城市建筑物高度和密度也有差别, 形成特殊的街道峡谷结构, 因此, 开展我国城市街道尺度大气边界层气象要素的精细观测将有助于完整认识我国城市街道建设对城市空气环境的影响.

参考文献
毕雪岩, 刘烽, 吴兑. 2005. 几种大气稳定度分类标准计算方法的比较分析[J]. 热带气象学报, 21(4): 402-409. DOI:10.3969/j.issn.1004-4965.2005.04.008
Depaul F T, Sheih C M. 1986. Measurements of wind velocities in a street canyon[J]. Atmospheric Environment, 20(3): 455-459. DOI:10.1016/0004-6981(86)90085-5
高海宁, 李元征, 韩风森, 等. 2017. 城市街道峡谷通风与空气污染研究进展[J]. 世界科技研究与发展, 39(4): 363-371.
蒋德海, 蒋维楣, 苗世光. 2006. 城市街道峡谷气流和污染物分布的数值模拟[J]. 环境科学研究, 19(3): 7-12. DOI:10.3321/j.issn:1001-6929.2006.03.004
Kennedy I M, Kent J H. 1977. Wind tunnel modelling of carbon monoxide dispersal in city streets[J]. Atmospheric Environment, 11(6): 541-547. DOI:10.1016/0004-6981(77)90073-7
Klein P M, Galvez J M. 2015. Flow and turbulence characteristics in a suburban street canyon[J]. Environmental Fluid Mechanics, 15(2): 419-438. DOI:10.1007/s10652-014-9352-5
Klein P, Clark J V. 2007. Flow variability in a north American downtown street canyon[J]. Journal of Applied Meteorology & Climatology, 46(46): 851-877.
Kwak K H, Baik J J. 2014. Diurnal variation of NOx and ozone exchange between a street canyon and the overlying air[J]. Atmospheric Environment, 86(3): 120-128.
李磊, 张立杰, 张宁, 等. 2010. FLUENT在复杂地形风场精细模拟中的应用研究[J]. 高原气象, 29(3): 621-628.
刘建峰, 王宝庆, 牛宏宏, 等. 2017. 计算流体力学模拟街道峡谷特征和风向对细颗粒物污染扩散的影响[J]. 环境污染与防治, 39(4): 367-374.
Nelson M A, Pardyjak E R, Klewicki J C, et al. 2015. Properties of the wind field within the Oklahoma City Park Avenue Street Canyon.Part Ⅰ:Mean flow and turbulence statistics[J]. Journal of Applied Meteorology & Climatology, 46(12): 2055-2073.
Nunez M, Oke T R. 1977. The energy balance of an urban canyon[J]. Journal of Applied Meteorology, 16(1): 11-19. DOI:10.1175/1520-0450(1977)016<0011:TEBOAU>2.0.CO;2
Oke T R. 1988. Street design and urban canopy layer climate[J]. Energy & Buildings, 11(1): 103-113.
Sabatino S D, Buccolieri R, Pulvirenti B, et al. 2008. Flow and pollutant dispersion in street canyons using FLUENT and ADMS-Urban[J]. Environmental Modeling Assessment, 13(3): 369-381. DOI:10.1007/s10666-007-9106-6
Shen C, Bao X, Tan J, et al. 2017. Two noise-robust axial scanning multi-image phase retrieval algorithms based on Pauta criterion and smoothness constraint[J]. Optics Express, 25(14): 16235-16249. DOI:10.1364/OE.25.016235
盛裴轩. 2013. 大气物理学[M]. 北京: 北京大学出版社.
Walton A, Cheng A, Yeung W C. 2002a. arge-eddy simulation of pollution dispersion in an urban street canyon-Part Ⅰ:comparison with field data[J]. Atmospheric Environment, 36(22): 3601-3613. DOI:10.1016/S1352-2310(02)00259-5
Walton A, Cheng A Y S. 2002b. Large-eddy simulation of pollution dispersion in an urban street canyon-Part Ⅱ:idealised canyon simulation[J]. Atmospheric Environment, 36(22): 3615-3627. DOI:10.1016/S1352-2310(02)00260-1
王纪武, 张晨, 冯余军. 2012. 街谷空气污染研究评述及城市规划应对框架[J]. 城市发展研究, 19(5): 82-87. DOI:10.3969/j.issn.1006-3862.2012.05.015
王乐, 张云伟, 顾兆林. 2012. 动态风场及交通流量下街道峡谷内污染物扩散模拟[J]. 中国环境科学, 32(12): 2161-2167. DOI:10.3969/j.issn.1000-6923.2012.12.008
幸鸿, 徐伟嘉, 蔡铭, 等. 2011. 含信号控制人行横道的街道峡谷污染物扩散三维数值模拟[J]. 环境科学学报, 31(10): 2102-2108.
徐伟嘉, 幸鸿, 余志. 2012. 路绿化带对街道峡谷内污染物扩散的影响研究[J]. 环境科学, 33(2): 532-538.
Zajic D, Fernando H J S, Calhoun R, et al. 2015. Flow and Turbulence in an Urban Canyon[J]. Journal of Applied Meteorology & Climatology, 50(1): 203-223.