2. 北京英特利为环境科技有限公司, 锐思计算智能实验室(RCIL), 北京 100085;
3. 南京智水环境科技有限公司, 南京 210012
2. Beijing Inteliway Environmental Sci. & Tech. Ltd., Rays Computational Intelligence Lab(RCIL), Beijing 100085;
3. Nanjing Innowater Co. Ltd., Nanjing 210012
水质模型已成为追踪污染物在水体中的迁移转化过程, 进行水环境管理的有效工具(Chinyama et al., 2014; Morelli et al., 2018; 邹锐等, 2018).随着监测数据的积累、监测技术的进步及对水体系统认知的深入(Vanderbilt et al., 2017), 建立高时空精度且能模拟水体系统复杂行为的三维水动力-水质模型具备了可行性; 与此同时, 流域的精细化管理要求建立精确的复杂水质模型, 以精准地指导流域污染防治(邹锐等, 2018).上述水质模型通常具有复杂的结构, 包含大量的方程和参数.参数取值的准确性会影响模型对水体系统表征的可靠性(Zou et al., 2009), 进而影响根据模型结果进行水环境管理的效果.在实践中, 大部分水质模型参数难以直接测得其准确值, 且部分参数因研究对象的不同而存在差异(Zwart et al., 2018), 因而需要根据监测数据对水质模型参数进行估值.
参数估值指在模型校准和验证阶段对参数值进行估计并调整, 以最大限度地降低实测值和模拟值之间差异的过程(Zou et al., 2009; Ostojski et al., 2016), 可分为手动调节法和自动估值法.试错法是常用的手动调节法, 该方法存在主观性强、效率低、无法表征参数的不确定性等问题(Zou et al., 2004).自动估值法可有效降低手动参数调节的主观性, 提高参数估值的效率, 是水质模型研究的重点(Zou et al., 2014; Wellen et al., 2015; Chaudhary et al., 2017; Yang et al., 2018).已有的研究提出了大量的模型参数自动估值方法, 包括广义似然不确定性估计(Stedinger et al., 2008)、遗传算法(Zou et al., 2007)、模拟退火(Borgomeo et al., 2015)、粒子群算法(Afshar et al., 2011)、协方差矩阵自适应进化(Rigosi et al., 2011)、蒙特卡洛马尔科夫链(Liang et al., 2016)、近似贝叶斯估计(Kavetski et al., 2018)等.然而, 由于复杂水质模型的运行需要耗费较长的时间, 而自动估值方法在参数寻优过程中需要的迭代次数很多, 需要的时间成本和计算资源很高, 大大限制了上述方法的应用, 也成为限制复杂水质模型在流域精细化管理中应用的瓶颈.在保证较高模型拟合效果的前提下, 提高模型参数自动估值的效率成为亟待解决的问题.
贝叶斯优化(Bayesian Optimization)是基于贝叶斯定理的非线性、全局、序贯优化方法(Mockus et al., 1978).该方法采用概率代理模型拟合目标函数, 根据采集函数主动选择下一个评估点, 具有收敛速度快、优化迭代次数少的优点, 尤其适用于求解优化目标存在多峰、非凸、黑箱及存在观测噪音等特点的问题(崔佳旭等, 2018).同时, 该方法应用领域广泛, 已经成为机器学习和人工智能领域参数学习的主流方法(Ghahramani, 2015; Shahriari et al., 2016; Cornejo-Bueno et al., 2018; 邓帅, 2019), 也被用于优化环境监测布点(Marchant et al., 2012)和水资源调度方案(Candelieri et al., 2018).此外, 高效并行算法的开发大大提高了贝叶斯优化的效率(Martinezcantin, 2014).尽管贝叶斯优化方法存在上述优点, 然而尚未有系统评估该方法在复杂水质模型参数估值中适用性的研究.因此, 本文提出一种基于贝叶斯优化的复杂水质模型参数估值方法, 并以云南异龙湖三维水动力水质模型为研究对象, 依据模型结果评估该方法在复杂水质模型参数估值中的适用性.
2 材料和方法(Materials and methods)本研究提出的基于贝叶斯优化的复杂水质模型参数估值方法如图 1所示.由于复杂水质模型包含大量参数, 而通常只有少数参数影响模型的输出(Yi et al., 2016); 对不重要或者不敏感的参数进行估值则会导致模型的过参数化, 大大降低参数估值的效率(Song et al., 2015; Jiang et al., 2018), 因而本研究在对参数进行估值之前需要进行敏感参数的选择(Jia et al., 2018):首先借鉴已有的研究结果, 选择对模型拟合效果有重要影响的参数; 然后采用敏感性分析方法, 对选择的重要参数进行敏感性排序, 并筛选出敏感参数; 其后, 采用贝叶斯优化方法对筛选出的参数进行估值; 最后, 通过分析参数估值方法的优化效率和水质模型的拟合效果, 对方法的适用性进行评估.下面对本研究中采用的关键方法, 即参数敏感性分析和贝叶斯优化方法进行详细阐述.
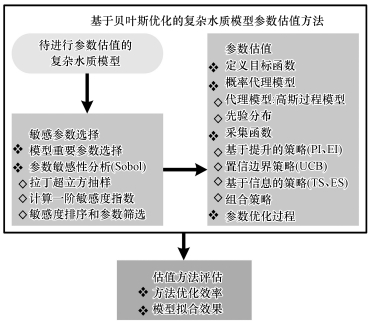 |
| 图 1 基于贝叶斯优化的复杂水质模型参数估值技术路线 Fig. 1 Technique route for the parameters estimation method based on Bayesian optimization for complex water quality models |
模型参数敏感性分析法包括筛选分析法、回归分析法、基于代理模型的方法和基于方差分解的方法等(宋晓猛等, 2015).Sobol法是一种基于方差分解的全局、定量参数敏感性分析方法(Nossent et al., 2011).与其它方法相比, 该方法能够获得更加稳健的敏感性指数结果和参数的敏感性排序(Tang et al., 2007; Yang, 2011), 适用于分析复杂非线性的参数敏感性排序(陈卫平等, 2017), 已被应用于复杂水质模型的参数敏感性分析研究中(Pastres et al., 1999; Cibin et al., 2010; 张质明等, 2014).本研究采用Sobol法对筛选出的重要参数的敏感度进行定量化.作为一种基于方差分解的敏感性分析方法, 根据方差分解的运算法则, Sobol法的基本原理可表述为(Song et al., 2015):
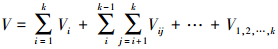
|
(1) |
式中, V表示模型输出(Y)的总方差, Vi (0 < i≤k, k为进行敏感性分析的参数个数)表示第i个参数(θi)的一阶方差, Vij表示第i、j个参数的二阶方差, 直到V1, 2, …, k表示全部参数的k阶方差, 满足式(2):
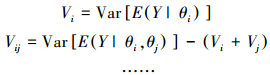
|
(2) |
其中, Vi又被称为主要效应, 用于表征参数对Y的主要影响; 则参数的一阶敏感度指数(Si)可表示为式(3).根据Si的大小即可判定不同参数的敏感度(Si越大则θi越敏感).
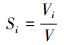
|
(3) |
对复杂水质模型进行参数估值, 可以视为寻找最优参数集θop使得未知目标函数f达到最大(或最小)的非线性优化问题(Zou et al., 2009):
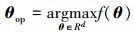
|
(4) |
式中, θ为模型参数集, Rd为参数的d维取值空间.贝叶斯优化过程利用了贝叶斯定理:
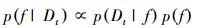
|
(5) |
式中, p(f)和p(f|Di)分别为f的先验和后验概率分布, p(f|Di)为似然函数, Dt为已观测集合, 满足如下递归关系:
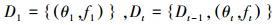
|
(6) |
式中, ft为与θt对应的目标函数值.
与其它优化算法一样, 在进行贝叶斯优化时应当首先选择目标函数, 即优化过程需要极大(小)化的统计量.贝叶斯优化方法包含2个关键部分:概率代理模型和采集函数(Snoek et al., 2012).贝叶斯优化算法可用较少的评估次数求得复杂目标函数的最优解, 原因在于使用概率代理模型拟合真实目标函数, 并根据采集函数主动选择最有潜力(损失函数最小)的评估点进行下一次评估, 避免不必要的采样(崔佳旭等, 2018).下面分别对目标函数、概率代理模型和采集函数进行阐述.
2.2.1 目标函数纳什效率系数(NSE)是最常用的模型评价指标之一(Bennett et al., 2013; Bae et al., 2018), 表示模型拟合方差占总方差的百分比(Nash et al., 1970).NSE受极高值影响较大, 对数NSE(lg(NSE))可有效地降低极值对模型总体拟合效果的影响(Harmel et al., 2014), 因而本研究选择lg(NSE)作为模型评价指标:
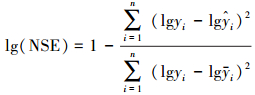
|
(7) |
式中, yi和
概率代理模型用于替代评估代价高昂的复杂目标函数, 根据贝叶斯定理不断地进行迭代以增加信息量, 对先验知识进行修正(Shahriari et al., 2016).根据模型参数个数是否固定, 概率代理模型可以分为参数模型和非参数模型.高斯过程函数具有高度的灵活性、可扩展性和可分析性, 对线性和非线性关系均具有良好的替代性(Jones, 2001), 因而成为贝叶斯优化中应用最广泛的概率代理模型(Snoek et al., 2012).
高斯过程是多元高斯概率分布的范化(Rasmussen et al., 2005), 由均值函数m(θ)和半正定的协方差函数k(θ, θ′)构成:
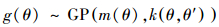
|
(8) |
在实践中, 为高斯过程的均值函数指定明确的先验信息是十分困难的, 因而为简便起见, 通常假设先验均值函数为零.这种设定对后验分布的准确性几乎没有影响(崔佳旭等, 2018), 因而本研究设定先验均值为0.协方差指定了未知目标函数的平滑线和振幅, 表征了2个计算点之间的相似性, 对于能否获得理想的预测效果具有重要影响(Snoek et al., 2012).Matérn协方差函数簇是一类高度灵活的协方差函数, 可产生二阶可微的样本函数, 其表达式为(崔佳旭等, 2018):
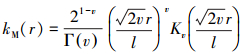
|
(9) |
式中, v为平滑参数, l为尺度参数, Kv为第二类变形贝塞尔函数.参照邓帅(2019)的研究, 本研究分别令v = 2.5、l = 1.
2.2.3 采集函数采集函数根据概率代理模型的后验结果构造主动选择策略, 通过其最大化决定下一个评估点θt+1的位置(Shahriari et al., 2016):
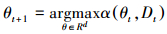
|
(10) |
式中, α(θt, Dt)为第t次迭代后的采集函数.采集函数需要兼顾优化进程的探测深度(exploitation, 提高目标函数的均值)和探测广度(exploration, 减小目标函数的不确定性), 因而根据采集函数确定的θt+1处的目标通常具有较高的平均值和较大的不确定性(Ghahramani, 2015).
采集函数可分为4种策略, 分别为基于提升的策略、置信边界策略、基于信息的策略和组合策略(Shahriari et al., 2016).当以高斯过程为概率代理模型时, 通常采用的采集函数包括提升概率(Probability of Improvement, PI)、期望提升量(Expected Improvement, EI)和置信上边界(Upper Confidence Bound, UCB)(Snoek et al., 2012).PI量化了各点可能提升当前最优目标函数值的概率(Kushner, 1963), 选择使当前目标值提升概率最大的点作为新的评估点, 其表达式为:
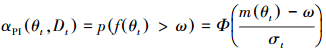
|
(11) |
式中, Φ(·)为标准正态分布的累积分布函数, ω为评估提升的阈值, 即f超过该值则认为优化效果提升, σt为f的方差.PI选择的是提升概率最大的评估点, 但PI将各点的提升看作是等量的, 只可反映提升的概率而不能反映提升量的大小.EI将提升概率和提升量整合起来, 其表达式为:
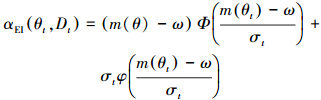
|
(12) |
式中, $φ$(·)为标准正态分布的概率密度函数.UCB为直接比较各点置信区间的上界, 可以视为均值(探测深度)和方差(探测广度)的线性加权, 其表达式为:
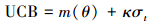
|
(13) |
式中, κ为权衡探测深度和广度的权重因子, κ越大则探测广度的权重越大.本研究分别选择上述3个函数进行优化, 且当选择UCB作为采集函数时, 取κ=2.5.
2.3 研究对象本研究以异龙湖为案例地, 以IWIND-LR模型为待进行参数估值的复杂水质模型.研究中采用的Sobol参数敏感性分析运用Matlab进行数值计算, 贝叶斯优化基于Python软件的BayesianOptimization模块.异龙湖(102°30′~102°38′E, 23°39′~23°42′N)位于云南省红河哈尼族彝族自治州石屏县境内, 湖泊总面积28.4 km2, 最大体积114.9万m3, 平均海拔1414 m, 平均水深3.9 m, 最大水深5.7 m, 全年平均水温约20 ℃, 由于风的扰动作用与湖水深度较浅, 水体处于完全混合状态.
本研究采用的复杂水质模型为IWIND-LR, 已被广泛地应用于支撑水质污染防治决策(王冰等, 2016; 张月霞等, 2018).IWIND-LR模型以国际上广泛应用的高级水动力水质模型—环境流体力学代码(EFDC)作为计算内核, 同时针对当前面临的环境问题, 在EFDC原始版本的基础上开发了一些高级模块.该模型包含三维水动力、温度动力学和内部耦合的水质模型模块, 能够实现湖泊内部水质过程的时空精确模拟.该模型可模拟26个水质变量, 模拟底泥与水体之间的营养盐交换及底泥对溶解氧的动态作用; 基于物质守恒定律, IWIND-LR模型能够模拟物理输送、大气交换、吸附解析、藻类吸收、底泥-水界面交换、硝化和反硝化、沉积成岩等过程(邹锐等, 2018).
本研究将异龙湖的地形和边界条件作为IWIND-LR的输入, 模型采用笛卡尔直角坐标网格, 共划分813个水平网格, 垂向采用σ坐标, 平均分为2层.模型计算步长为15 s, 模拟时间为365 d.模型所用的输入条件和边界条件以异龙湖2008年9月—2009年8月的气象、8条入湖和1条出湖河流出入流流量与浓度的实测值为基础.为了增加模型复杂度和非线性水平, 对原有入湖流量和浓度进行了随机扰动, 由此产生的模型输入文件中设置的入湖负荷值比实际情况要高, 边界条件也具有比实际数据更显著的时空变异性.
参数估值所用的观测值为通过随机组合关键参数与边界条件而生成的合成观测值, 所以合成观测值的范围可能与实测数据范围有一定差异.模型可模拟不同的水质指标, 从而输出各网格点上对应的水质指标时间序列值, 本研究选择5种目前被重点关注的水质指标进行模拟, 分别为叶绿素a(Chla)、总氮(TN)、氨氮(NH3-N)、总磷(TP)和溶解氧(DO).通过不同指标的同时模拟, 一方面可以避免单个水质指标参数估值时可能引起的“过拟合”现象, 同时也可以降低参数选取的不确定性(Mockus et al., 1978).合成观测值来自于15个分布较为均匀的空间站点(图 2), 模拟时间为1年, 监测频次为每2周1次, 共24组监测数.
 |
| 图 2 站点1~15空间分布图 Fig. 2 Locations map of Sta1~Sta15 |
基于对浅水湖泊系统污染物迁移转化机理过程的认识, 可以选择对模型具有重要影响的参数.例如, 在分析太湖藻类模型的参数敏感性时, 姜龙等(2018)筛选出40个重要的水质指标.异龙湖位于云南省, 因而本研究首先根据伊璇等(2017)对云贵高原湖泊(滇池)复杂水质模型(EFDC)的分析结果, 选择32个重要的模型参数用于敏感性分析, 包括与不同藻类的生长、捕食、沉降速率相关的参数及营养盐的衰减和水解速率等.
Sobol敏感性分析包括如下5个步骤:①采用拉丁超立方抽样方法(Mckay et al., 2000), 对32个参数进行60次抽样, 生成30×32的A、B两个矩阵; ②将B矩阵的第i列与A矩阵的第i列替换, 生成用于计算第i个参数敏感性的输入矩阵ABi, 据此可构造矩阵AB1~ AB32; ③将上述新构造的32个矩阵与A、B两个矩阵代入模型运行, 得到模型结果; ④计算一阶敏感度指数; ⑤对各个参数在时间和水质指标上的敏感度求平均, 并将32个参数的敏感度指数进行归一化.选择归一化后敏感度指数大于0.2的参数作为敏感参数, 共得到10个参数(表 1).
| 表 1 筛选出的敏感性参数 Table 1 Filtered sensitivity parameters |
贝叶斯优化算法的决策变量为上述10个敏感参数, 目标函数为5项水质指标的lg(NSE)平均值.以高斯过程为概率代理模型, 采用PI、EI、UCB 3种采集函数进行贝叶斯优化, 设置优化的迭代次数为300次.此外, 还需设定lg(NSE)的目标阈值, 若优化结果未达到目标阈值则重新进行参数优化, 保证不同的组合情况都达到最优解.本研究设定目标阈值为0.6.
为避免初值对优化结果的影响, 本研究共设置10种不同的组合进行贝叶斯优化, 该过程共占用5台双核计算机, 计算时间约30 d, 其中, 复杂水质模型IWIND-LR运行一次约需1 h.采用目视法, 根据贝叶斯优化时lg(NSE)的变化情况, 可以判断收敛情况.图 3展示了采集函数为UCB时lg(NSE)值随迭代次数的变化情况, 由图中的黑色趋势线可知, 该算法在前30次迭代时lg(NSE)值上升迅速, 在50次迭代之后lg(NSE)值稳步缓慢上升, 方差逐渐减小, 表明算法此时已接近收敛.
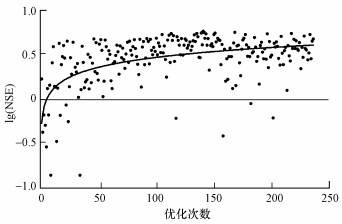 |
| 图 3 采集函数为UCB时贝叶斯优化过程的目标函数值 (黑色菱形表示优化过程中的目标函数最大值点) Fig. 3 The objective function values of the Bayesian optimization process when the acquisition function is UCB |
不同采集函数收敛所需的迭代次数见表 2, 可见3种采集函数在300次迭代之内均已表现出良好的收敛性.相比而言, EI作为采集函数时收敛所需要的迭代次数仅为PI或UCB作为采集函数时所需收敛次数的1/2, 因而EI具有更高的收敛效率; UCB作为采集函数的收敛效率略高于PI.常用的进化算法在复杂水质模型参数估值时, 通常需要经过成千上万次迭代才能找到较优解; 在本案例中, 采用贝叶斯优化方法可在很少的迭代次数下快速地找到较优解, 表明该方法用于复杂水质模型的参数估值时, 具有收敛速度快、运算效率高的特点.
| 表 2 不同采集函数收敛所需的迭代次数和目标函数值 Table 2 Number of iterations and objective function values required for convergence of different acquisition functions |
进行参数估值后模型lg(NSE)均大于0.65(表 2), 表明模型达到了满意的级别(Ritter et al., 2013).运用采集函数为UCB的最优解对模型进行校正, 限于篇幅, 仅列出校正后的模型模拟值与观测值的Chla、DO对比结果(图 4).由图可知, 模型可很好地捕捉到不同水质指标的时空变化和协同变化规律:①除了部分站点的NH3-N和少量站点的Chla和DO外, 大部分站点的大部分指标均表现出良好的拟合效果; ②在时间上, 模型很好地捕捉了Chla、DO和营养盐的季节性变化, 尤其准确拟合了夏、秋季节水质较差阶段Chla和营养盐浓度较高的特征; ③在空间上, 模型很好地刻画了水质指标的空间分布模式, Sta01的污染物浓度显著高于其它站点, Sta04和Sta05处于过渡状态, 其它站点则明显低于这3个站点; ④对于不同水质指标的协同变化, 模型很好地体现了营养盐和Chla浓度受季节性驱动因子导致的年内协同变化特征, 很好地刻画了夏、秋季由于藻类生长导致的DO过饱和现象.上述结果表明, 采用贝叶斯优化进行参数估值后的复杂水质模型对观测值具有良好的拟合效果.
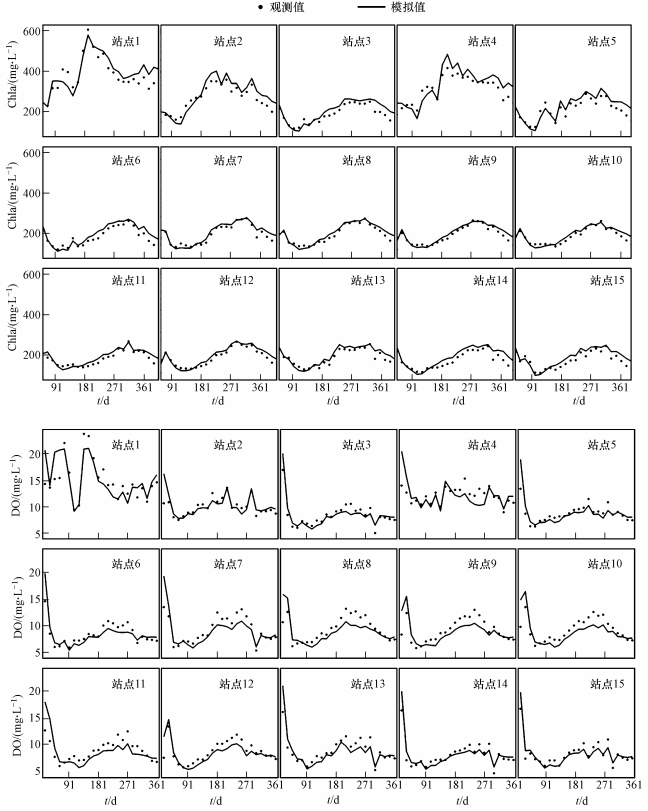 |
| 图 4 15个站点的Chla和DO模拟值与观测值对比 Fig. 4 Comparison of simulated and observed values of Chla and DO at 15 sites |
在本研究中, 尽管采用贝叶斯优化方法相对于其它需要进行成千上万次迭代的进化算法具有高效性, 但必须注意到完整进行一次贝叶斯优化过程也需较长时间(10 d左右).因而有必要开展研究揭示影响贝叶斯优化效率的因素, 进一步地减少运算所需时间.
从水质模型的敏感参数选取来看, 由于本研究借鉴滇池EFDC模型的结果(伊璇等, 2017), 选择了32个重要参数进行参数敏感性分析, 而未对异龙湖IWIND-LR模型进行重要参数选取, 因此, 可能导致高敏感度参数的漏选或错选, 从而降低了优化效率(Jiang et al., 2018).由于敏感性分析时相对于贝叶斯优化的运算量小很多, 因而未来在进行敏感性分析时可选择更多的参数进行敏感性分析.
从概率代理模型和采集函数的参数取值和形式来看, 高斯过程Matérn协方差函数的尺度参数和平滑参数, 以及采集函数的权重系数均可能对优化效率产生影响(Shahriari et al., 2016).由于本研究是采用贝叶斯优化方法对复杂水质模型进行参数估计的首例, 因而对于参数的设定并无成熟经验借鉴; 本研究借鉴在机器学习领域的相关参数的设定(邓帅, 2019), 可能并不适用于复杂水质模型的替代及探测深度和广度的权衡.此外, 概率代理模型和采集函数还存在其他选择, 本研究尚未进行探索.因此, 未来应探究不同参数取值对优化效率的影响, 通过大量案例研究给出适用于复杂水质模型参数估值的模型形式和参数取值, 为贝叶斯优化方法的应用提供指导.
从贝叶斯优化的运行方法来看, 通过采用近似技术、超参数优化技术和采集函数优化技术可以大大提高优化效率, 降低运算时间(崔佳旭等, 2018).因此, 未来应探究这些方法在复杂水质模型参数估值中的应用, 进一步提高贝叶斯优化效率.
4 结论(Conclusions)针对传统方法在复杂水质模型参数估值中效率低下的难题, 本研究提出一种基于贝叶斯优化方法的参数估值方法, 并在对异龙湖IWIND-LR模型进行参数估值的研究中发现, 当贝叶斯优化算法的采集函数为EI时, 仅需要141次迭代lg(NSE)即可达到0.766, 表明本研究提出的方法具有较高的优化效率, 且能保证参数优化后的水质模型具有较好的拟合效果, 同时也验证了该方法在复杂水质模型参数估值中的适用性.未来可从水质模型敏感参数的选择、贝叶斯优化方法中参数取值和函数形式及优化过程近似和优化等方面进行研究, 进一步提高该方法的效率.
Afsh ar A, Kazemi H, Saadatpour M. 2011. Particle swarm optimization for automatic calibration of large scale water quality model (CE-QUAL-W2):Application to Karkheh Reservoir, Iran[J]. Water Resources Management, 25(10): 2613–2632.
DOI:10.1007/s11269-011-9829-7
|
Bae S, Seo D. 2018. Analysis and modeling of algal blooms in the Nakdong River, Korea[J]. Ecological Modelling, 372: 53–63.
DOI:10.1016/j.ecolmodel.2018.01.019
|
Bennett N D, Croke B F W, Guariso G, et al. 2013. Characterising performance of environmental models[J]. Environmental Modelling & Software, 40: 1–20.
|
Borgomeo E, Farmer C L, Hall J W. 2015. Numerical rivers:A synthetic streamflow generator for water resources vulnerability assessments[J]. Water Resources Research, 51(7): 5382–5405.
DOI:10.1002/2014WR016827
|
陈卫平, 涂宏志, 彭驰, 等. 2017. 环境模型中敏感性分析方法评述[J]. 环境科学, 2017, 38(11): 4889–4896.
|
崔佳旭, 杨博. 2018. 贝叶斯优化方法和应用综述[J]. 软件学报, 2018, 29(10): 3068–3090.
|
Candelieri A, Perego R, Archetti F. 2018. Bayesian optimization of pump operations in water distribution systems[J]. Journal of Global Optimization, 71(1): 213–235.
DOI:10.1007/s10898-018-0641-2
|
Chaudhary A, Hantush M M. 2017. Bayesian Monte Carlo and maximum likelihood approach for uncertainty estimation and risk management:Application to lake oxygen recovery model[J]. Water Research, 108: 301–311.
DOI:10.1016/j.watres.2016.11.012
|
Chinyama A, Ochieng G M, Nhapi I, et al. 2014. A simple framework for selection of water quality models[J]. Reviews in Environmental Science and Bio-Technology, 13(1): 109–119.
DOI:10.1007/s11157-013-9321-3
|
Cibin R, Sudheer K P, Chaubey I. 2010. Sensitivity and identifiability of stream flow generation parameters of the SWAT model[J]. Hydrological Processes, 24(9): 1133–1148.
DOI:10.1002/hyp.v24:9
|
Cornejo-Bueno L, Garrido-Merchan E C, Hernandez-Lobato D, et al. 2018. Bayesian optimization of a hybrid system for robust ocean wave features prediction[J]. Neurocomputing, 275: 818–828.
DOI:10.1016/j.neucom.2017.09.025
|
邓帅. 2019. 基于改进贝叶斯优化算法的CNN超参数优化方法[J]. 计算机应用研究, 2019, 36(7): 1–2.
|
Ghahramani Z. 2015. Probabilistic machine learning and artificial intelligence[J]. Nature, 521(7553): 452–459.
DOI:10.1038/nature14541
|
Harmel R D, Smith P K, Migliaccio K W, et al. 2014. Evaluating, interpreting, and communicating performance of hydrologic/water quality models considering intended use:A review and recommendations[J]. Environmental Modelling & Software, 57: 40–51.
|
姜龙, 李一平, 章双双, 等. 2018. 大型浅水湖泊藻类模型参数敏感性分析[J]. 湖泊科学, 2018, 30(3): 693–700.
|
Jia H, Xu T, Liang S, et al. 2018. Bayesian framework of parameter sensitivity, uncertainty, and identifiability analysis in complex water quality models[J]. Environmental Modelling & Software, 104: 13–26.
|
Jiang L, Li Y, Zhao X, et al. 2018. Parameter uncertainty and sensitivity analysis of water quality model in Lake Taihu, China[J]. Ecological Modelling, 375: 1–12.
DOI:10.1016/j.ecolmodel.2018.02.014
|
Jones D R. 2001. A taxonomy of global optimization methods based on response surfaces[J]. Journal of Global Optimization, 21(4): 345–383.
DOI:10.1023/A:1012771025575
|
Kavetski D, Fenicia F, Reichert P, et al. 2018. Signature-domain calibration of hydrological models using approximate bayesian computation:Theory and comparison to existing applications[J]. Water Resources Research, 54(6): 4059–4083.
DOI:10.1002/2017WR020528
|
Kushner H J. 1963. A new method of locating the maximum point of an arbitrary multipeak curve in the presence of noise[J]. Journal of Fluids Engineering, 86(1): 97–106.
|
Liang S, Jia H, Xu C, et al. 2016. A Bayesian approach for evaluation of the effect of water quality model parameter uncertainty on TMDLs:A case study of Miyun Reservoir[J]. Science of the Total Environment, 560: 44–54.
|
Marchant R, Ramos F.2012. Bayesian Optimisation for Intelligent Environmental Monitoring[C].IEEE/RSJ International Conference on Intelligent Robots and Systems.Vilamoura, Algarve: 2242-2249
|
Martinezcantin R. 2014. BayesOpt:A bayesian optimization library for nonlinear optimization, experimental design and bandits[J]. Journal of Machine Learning Research, 15: 3735–3739.
|
Mckay M D, Beckman R J, Conover W J. 2000. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code M.D. Mckay[J]. Technometrics, 21(2): 266–294.
|
Mockus J, Tiesis V, Zilinskas A. 1978. The Application of Bayesian Methods for Seeking the Extremum[M]. Amsterdam: North-Holland.
|
Morelli B, Hawkins T R, Niblick B, et al. 2018. Critical review of eutrophication models for life cycle assessment[J]. Environmental Science & Technology, 52(17): 9562–9578.
|
Nash J E, Sutcliffe J V. 1970. River flow forecasting through conceptual models part I — A discussion of principles[J]. Journal of Hydrology, 10(3): 282–290.
DOI:10.1016/0022-1694(70)90255-6
|
Nossent J, Elsen P, Bauwens W. 2011. Sobol′ sensitivity analysis of a complex environmental model[J]. Environmental Modelling & Software, 26(12): 1515–1525.
|
Ostojski M S, Gebala J, Orlinska-Wozniak P, et al. 2016. Implementation of robust statistics in the calibration, verification and validation step of model evaluation to better reflect processes concerning total phosphorus load occurring in the catchment[J]. Ecological Modelling, 332: 83–93.
DOI:10.1016/j.ecolmodel.2016.04.004
|
Pastres R, Chan K, Solidoro C, et al. 1999. Global sensitivity analysis of a shallow-water 3D eutrophication model[J]. Computer Physics Communications, 117(1/2): 62–74.
|
Rasmussen C E, Williams C K I. 2005. Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning)[M]. Cambridge, MA: The MIT Press.
|
Rigosi A, Marce R, Escot C, et al. 2011. A calibration strategy for dynamic succession models including several phytoplankton groups[J]. Environmental Modelling & Software, 26(6): 697–710.
|
Ritter A, Muñoz-Carpena R. 2013. Performance evaluation of hydrological models:Statistical significance for reducing subjectivity in goodness-of-fit assessments[J]. Journal of Hydrology, 480(4): 33–45.
|
Shahriari B, Swersky K, Wang Z, et al. 2016. Taking the human out of the loop:a review of bayesian optimization[J]. Proceedings of the IEEE, 104(1): 148–175.
|
Snoek J, Larochelle H, Adams R P. 2012. Practical bayesian optimization of machine learning algorithms[J]. Advances in Neural Information Processing Systems, 2: 2951–2959.
|
Song X, Zhang J, Zhan C, et al. 2015. Global sensitivity analysis in hydrological modeling:Review of concepts, methods, theoretical framework, and applications[J]. Journal of Hydrology, 523: 739–757.
DOI:10.1016/j.jhydrol.2015.02.013
|
Stedinger J R, Vogel R M, Lee S U, et al. 2008. Appraisal of the generalized likelihood uncertainty estimation (GLUE) method[J]. Water Resources Research, 44(12): 1–10.
|
宋晓猛, 张建云, 占车生, 等. 2015. 水文模型参数敏感性分析方法评述[J]. 水利水电科技进展, 2015, 35(6): 105–112.
|
Tang Y, Reed P, Wagener T, et al. 2007. Comparing sensitivity analysis methods to advance lumped watershed model identification and evaluation[J]. Hydrology and Earth System Sciences, 11(2): 793–817.
DOI:10.5194/hess-11-793-2007
|
Vanderbilt K, Porter J H, Lu S S, et al. 2017. A prototype system for multilingual data discovery of International Long-Term Ecological Research (ILTER) Network data[J]. Ecological Informatics, 40: 93–101.
DOI:10.1016/j.ecoinf.2016.11.011
|
Wellen C, Kamran-Disfani A R, Arhonditsis G B. 2015. Evaluation of the current state of distributed watershed nutrient water quality modeling[J]. Environmental Science & Technology, 49(6): 3278–3290.
|
王冰, 刘晓威, 王灵志, 等. 2016. 基于IWIND-LR模型的河流突发性溢油事故模拟与应急响应分析[J]. 安全与环境工程, 2016, 23(4): 148–153.
|
Yang J. 2011. Convergence and uncertainty analyses in Monte-Carlo based sensitivity analysis[J]. Environmental Modelling & Software, 26(4): 444–457.
|
Yang J, Jakeman A, Fang G, et al. 2018. Uncertainty analysis of a semi-distributed hydrologic model based on a Gaussian Process emulator[J]. Environmental Modelling & Software, 101: 289–300.
|
Yi X, Zou R, Guo H. 2016. Global sensitivity analysis of a three-dimensional nutrients-algae dynamic model for a large shallow lake[J]. Ecological Modelling, 327: 74–84.
DOI:10.1016/j.ecolmodel.2016.01.005
|
伊璇, 郭怀成. 2017. 三维水动力水质模型不确定性研究[M]. 北京: 科学出版社.
|
张月霞, 谢骏. 2018. IWIND-LR模型在抚仙湖水位模拟中的应用[J]. 环境科学导刊, 2018, 37(3): 46–51.
|
张质明, 王晓燕, 李明涛. 2014. 基于全局敏感性分析方法的WASP模型不确定性分析[J]. 中国环境科学, 2014, 34(5): 1336–1346.
|
邹锐, 苏晗, 余艳红, 等. 2018. 基于水质目标的异龙湖流域精准治污决策研究[J]. 北京大学学报(自然科学版), 2018, 54(2): 426–434.
|
Zou R, Lung W S, Wu J. 2007. An adaptive neural network embedded genetic algorithm approach for inverse water quality modeling[J]. Water Resources Research, 43(8): 1–13.
|
Zou R, Lung W S, Wu J. 2009. Multiple-pattern parameter identification and uncertainty analysis approach for water quality modeling[J]. Ecological Modelling, 220(5): 621–629.
DOI:10.1016/j.ecolmodel.2008.11.021
|
Zou R, Lung W S. 2004. Robust water quality model calibration using an alternating fitness genetic algorithm[J]. Journal of Water Resources Planning & Management, 130(6): 471–479.
|
Zou R, Zhang X, Liu Y, et al. 2014. Uncertainty-based analysis on water quality response to water diversions for Lake Chenghai:A multiple-pattern inverse modeling approach[J]. Journal of Hydrology, 514: 1–14.
DOI:10.1016/j.jhydrol.2014.03.069
|
Zwart J A, Hanson Z J, Vanderwall J, et al. 2018. Spatially explicit, regional-scale simulation of lake carbon fluxes[J]. Global Biogeochemical Cycles, 32(9): 1276–1293.
DOI:10.1002/2017GB005843
|
 2019, Vol. 39
2019, Vol. 39


