2. 山东科技大学, 青岛 266590;
3. 环境保护部环境规划院, 北京 100012
2. Shandong Universtity of Science and Technology, Qingdao 266590;
3. Chinese Academy for Environmental Planning, Beijing 100012
近年来, 以PM2.5为重要组分的雾霾污染高度频发, 已成为全民关注的热点环境问题.PM2.5粒径小, 富含大量的有毒、有害物质且在大气中的停留时间长、输送距离远, 不仅对空气质量和能见度等有重要的影响, 而且对人体健康和大气环境质量影响更大(蔡刚, 2012).为了强化对PM2.5的监管与防控, 国务院颁布的《环境空气质量标准》(2012版)增加了PM2.5监测指标, 各级政府及相关部门也发布了涵盖PM2.5因子的空气质量等级预报预警制度.考虑到大气环境的时效性及动态性, 实现精准的PM2.5浓度时空分布预测, 是支撑重大空气污染事件预警工作的基础, 亦是当前空气污染预警的重要研究方向.
目前大气污染物浓度预测方法主要有统计模型和确定性模型两类(王平等, 2017).其中, 统计模型一般是基于历史数据建立空气质量与影响因素之间的关联模型, 其优点在于对输入数据要求相对较低, 但预测精度较低, 难以反映区域空气质量且无法对污染成因及来源等给出合理解释;数值模型则是依据不同尺度大气动力学理论, 耦合大气物理和化学变化过程, 建立多尺度类型大气污染物扩散模型, 依靠计算机系统预报大气污染物浓度变化趋势和动态分布情况, 其优点是能够对污染成因进行诊断, 计算精确, 能够对区域内大气污染物浓度进行预测, 其局限性在于时效性污染排放数据获取困难, 模型对数据要求高, 实际操作困难较大(谢涛等, 2011).
鉴于数值预报所需成本较高, 存在较多的不确定因素, 模型建立过程和数据需求要求较复杂, 众多的研究倾向于以统计模型为主要手段开展大气污染物浓度预测, 特别是针对单站点统计模型预报开展了大量的改进研究.如在传统统计预报模式(主要依靠对历史空气质量、气象数据的分析处理, 从而外推得出对未来空气质量预报结果(刘小兵, 2016))的基础上, 很多研究者将传统的统计学方法与与神经网络模型、自回归移动平均模型、多元线性回归模型相结合获得了较为理想的预测结果(谭德彪, 2003).而从方法学的角度来看, 自回归移动平均模型和多元线性回归模型均是线性模式, 某些非线性的关系很难被精确预测, 这种缺陷已在某些实例研究中体现出来(向昌盛等, 2010);神经网络模型作为一种非线性映射方法, 其多层感知模式使得神经网络模型在细微颗粒物浓度预测方面有良好的效果(沈路路等, 2011).但神经网络方法的学习速度通常比较慢, 参数设定困难, 并且容易陷入局部最优, 推广能力差, 而且预测效率较低(张海艳, 2011).支持向量机(SVM)的出现克服了神经网络训练时间长、泛化能力差、易陷入局部极小等缺点(刘伟等, 2013).刘小兵(2016)运用支持向量回归机建立了PM2.5浓度预测模型, 试验结果表明, 单步预测效果良好, 但在进行多步预测时, 每步预测都需要上次预测的输出作为输入, 在这种迭代的过程中, 上一次的预测结果会影响在接下来时间点的预测结果, 误差也就会逐步积累到最后, 预测效果逐步减弱.
基于上述论述, 本研究提出一种基于小波分解(Wavelet Decomposition)自适应残差修正(Adaptive Multiple Layer Residual Correction)的最小二乘支持向量回归(Least Squares Support Vector Regression)的PM2.5短期预测模型.该模型涵盖数据处理单元、参数寻优单元和支持向量回归预测等单元, 以弥补预测值与真实值存在偏差所带来的预测不确定性问题, 并对预测残差进行方差估计得到预测结果在某一置信区间的上界, 在一定程度上降低预测的难度, 给公众提供在一定范围内可靠的PM2.5浓度水平, 并将为重污染天气预警方案风险评估提供技术支持.
2 材料与方法(Materials and methods) 2.1 研究区域济南位于山东省中西部, 南依泰山, 北跨黄河, 背山面水, 属泰山山脉的北缘, 由此引起的山风和谷风对济南地区的局地环流有着重要影响, 不利于污染物的扩散.南部石灰岩山区生态环境脆弱, 植被发育较差, 北部黄河冲洪积物, 土质松散, 遇大风地面易起风沙扬尘(翁剑桥, 2010).冬季受来自西伯利亚的西北风影响较大, 夏季主要受来自海上的东南风影响.由于特殊的地理形势, 南部山区挡住了冬季气流的南下, 夏季东南风也受到山区的层层阻挡, 所以济南特别是城区特殊的气流非常不利于污染物的扩散.
济南是PM2.5污染的重灾区, 其污染来源复杂, 污染物浓度控制因素众多, 动态浓度变化呈现非线性, 且与其相关的各个影响因素的信息很难准确获取.如何在有限信息中提取出更多的特征, 更加快速、准确、有效地进行预测, 对于济南市PM2.5防控具有很高的研究价值和实际应用价值.
2.2 研究数据数据来源于山东省环境信息与监控中心发布的山东省城市环境空气质量信息, 以及科干所监测站的日均值监测数据, 数据集涵盖2013年1月1日-2017年8月15日(共1677个数据), 其中1000个数据作为训练集, 其余677个数据作为测试集.
2.3 研究方法如图 1所示, 本研究针对PM2.5时序数据, 利用小波分解进行时频分析, 将一维信息扩展为高维信息, 提取PM2.5历史数据的隐含信息, 然后构建基于自适应多级残差修正的非线性最小二乘支持向量回归(AMLRC-LSSVR)预测模型, 最后对模型预测结果做方差分析, 得到置信区间的上界值作为最终的预测结果.
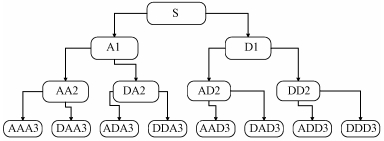 |
| 图 1 小波分解示意图 Fig. 1 The diagram of wavelet decomposition |
小波分解是采用有限长或快速衰减的振荡波形通过缩放和平移来表征信号, 基于时间和频率的局部变换, 进而有效地从信号(研究数据)中提取信息, 较好地扩展了傅里叶变换的应用(陈国初等, 2011).对于小波分析的理解, 可假定一个信号S通过3层分解来说明, 分解树见图 1.
在信号分析的过程中, 采用不同的小波基函数作为处理工具, 所得的结果有明显差异, 要想得到高精度的预测结果, 必须选择合理的小波基(陈倩倩, 2013).目前在工程领域对于小波基的选取并没有一个明确的标准, 大都依据经验或信号处理的目的来选取小波(龚海鹏, 2008).一般在支撑长度、消失矩、正则性上权衡处理, 考虑到将小波分解应用于PM2.5浓度时间序列的特征提取与预测中, 特征提取与预测的实时性和时频局部化能力, 本文结合小波基的性质, 综合分析发现, coif3小波优势明显:在消失矩上, coif3小波可以通过更少的分级层数对原始信号进行有效分解, 支撑长度较短, 从而滤波器长度较短, 小波分解计算量小(崔治等, 2013), 这样既能满足对信号的处理性能, 又能够降低计算量, 有助于提高在线预测效率.
2.3.2 最小二乘支持向量回归(LSSVR)最小二乘支持向量回归(LSSVR)是一种基于统计学习理论的建模方法(石亚欣, 2014), 具有训练速度快、泛化性能较好、拟合非线性函数能力强的特点.LSSVR是支持向量机回归(SVR)的一个重要分支, 与支持向量机回归相似, 训练算法为解凸二次优化问题, 具有全局唯一解, 它通过非线性映射ϕ(x)将输入空间映射到高维特征空间, 在特征空间中求取最优先性函数(谢屹鹏等, 2010).但LSSVR的求解算法由凸二次优化问题转变为求解线性方程组问题, 求解变量个数由2n+1个减少到n+1个(n为训练样本个数), 因此, LSSVR算法较SVR求解难度低, 并且训练速度快.设训练数据集为{(xi, yi)}i=1n, 输入xi∈Rd, 输出yi∈R, 则LSSVR可以表示为:
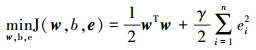
|
(4) |
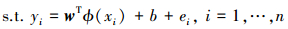
|
(5) |
式中, ϕ(x)是输入空间到高位特征空间的非线性映射;w是权向量, 表征模型的复杂度;e =[e1, e2, …, en]T是误差向量;γ∈R+是正则化参数;b是松弛变量.
根据Suykens给出的算法, 最终得到LSSVR模型预测函数如下所示:
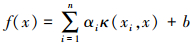
|
(8) |
基于多级残差修正的非线性最小二乘支持向量回归(MLRC-LSSVR)预测模型可以描述如下:①训练输入:训练数据集(Xtrain, Ytrain)∈ R(n-1)×2, 其中, Xtrain={PM2.51, PM2.52, …PM2.5n-1}, Ytrain={PM2.52, PM2.53, …PM2.5n};②预测输出:n+1时刻PM2.5污染物的预测浓度Ypredict=PM2.5n+1.
本方法可以利用n时刻数据及历史特征来预测n+k时刻的状态, 当k>1时, n+(k-1)时刻的数据也非真实值, 经过多次迭代后, 预测精度可能会较差, 预测t+1时刻的状态精度最高.其工作原理主要包括模型训练过程和模型预测过程两部分, 其中, 模型训练过程的工作步骤描述如下.
步骤1:对训练数据集中Xtrain进行coif3小波变换, 得到m层高维输入训练矩阵X′train={X′train, 1, X′train, 2, …, X′train, n-1}, 其中, X′train, i=(Am, traini, D1, traini, …, Dm, traini), i=1, 2, …, n-1, 构造LSSVR模型训练数据集(X ′train, Ytrain)∈R(n-1)×(m+2).
步骤2:基于训练数据集(X′train, Ytrain)对LSSVR模型进行训练, 训练过程采用搜索效率较高的simplex方法和10折交叉验证, 优化搜索LSSVR的高斯核函数关键参数, 并得到LSSVR训练终值Y′train.
步骤3:计算LSSVR训练终值Y′train与Ytrain之间的决定系数R2(Y′train, Ytrain).
步骤4:如果决定系数R2(Y′train, Ytrain)小于预设的决定系数阈值, 则计算训练残差向量并构造残差训练数据集(X′train, Ytrain= Ytrain- Y′train), 并重复步骤2和3, 直至模型满足决定系数阈值, 从而构造MLRC-LSSVR预测模型, 通过额外k-1个LSSVR残差预测模型实现对预测残差的在线同步修正, 其中, k为MLRC-LSSVR预测模型层级.
模型预测过程的工作步骤描述如下:
步骤1:重构n时刻的预测数据集Xpredict={Xtrain, Xpredict}, 其中, Xpredict=PM2.5n, 对Xpredict进行coif3小波分解, 得到n时刻的高维输入预测向量X′predict=(Am, predict, D1, predict, …, Dm, predict).
步骤2:将高维输入预测向量X′predict输入MLRC-LSSVR预测模型, 得到MLRC-LSSVR多级预测输出{Y′predict, RC1, predict, …, RCk-1, predict}, 从而得到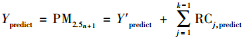
步骤3:基于中心极限理论进行线性平滑和偏置修正, 对残差(RCk-1, train, RCk-1, predict)进行方差估计, 从而得到相应的预测置信上界YPpredict=Ypredict+RCPk-1, predict, 其中, RCPk-1, predict为k-1级残差的97%置信估计方差.
如图 2所示, 重复步骤1~3的模型预测过程, 可以实现PM2.5预测浓度的在线预测和置信上限估计.此外, 随着PM2.5浓度时序的不断更新, 为了消除长期历史稳态偏置信息的冗余, 所构造的MLRC-LSSVR预测模型, 可以结合时序区间更新数据定期重复上述训练过程, 提高模型在线预测的有效性.
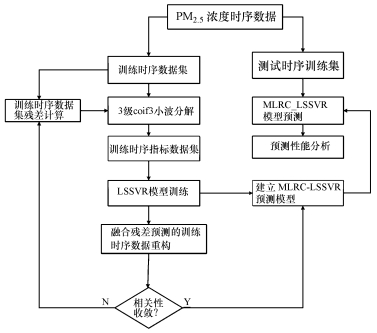 |
| 图 2 MLRC-LSSVR预测模型流程示意图 Fig. 2 The modeling step of MLRC-LSSVR |
济南市科干所监测站监测数据(2013年1月1日-2017年8月15日)时间序列分析如图 3所示, PM2.5浓度日均值波动比较大, 呈现出很强的随机性.以月为时间尺度来看, 周期性特征明显, 污染最严重时期出现在每年的12月和1月, 且呈现冬高、春弱、秋低、夏波动的明显现象.济南常年主导风向为西南风, 次主导风向为东北风, 冬季采暖期污染物排放量大, 且常遇静风、逆温、准静止锋及西南低气压等不利于污染物扩散的气象条件, 如出现环境空气强污染过程, 将导致污染物浓度大幅度升高.
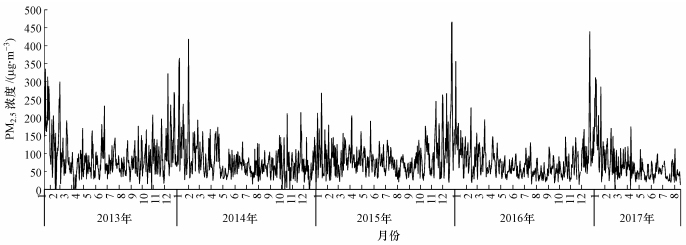 |
| 图 3 科干所监测站PM2.5日均浓度序列 Fig. 3 The series of PM2.5 daily mean concentration in Kegansuo monitoring station |
由图 3可以看出, 最大峰值的出现呈现出很强的周期性, 周期约为12个月, 最大峰值均大于300 μg · m-3;每月也会出现一次PM2.5较大的污染状况, 峰值在100 μg · m-3左右, 同时呈现出月内日均值波动较大的特点.
通过蒙特卡洛分析, 得出研究时间内(2013年1月1日-2017年8月15日), 该监测站PM2.5监测数据的概率分布及累计概率分布(图 4).该站点PM2.5浓度主要集中在20~170 μg · m-3之间, 其中,40~80 μg · m-3段发生的概率最大, 说明总体上该监测站附近PM2.5状况以良为主, 但也可以看出, 发生中度及重度污染天气的概率依然很大, 同时存在发生严重污染的风险, 其中有5%的可能性PM2.5浓度大于168 μg · m-3.
 |
| 图 4 科干所监测站PM2.5日均值浓度概率分布(a)及累积分布(b)示意图 Fig. 4 The probability distribution(a) and the cumulative distribution(b) of PM2.5 daily mean concentration probability in Kegansuo monitoring station |
PM2.5日均值浓度序列是非平稳时间序列数据, 通过小波变换将PM2.5浓度数据分解为由不同组成部分构成的序列组, 这些子序列相较于原数据具有更稳定的方差和较少的奇异值点, 能更有效、准确地表达原信号信息, 因此, 预测准确性更好(Jazebi et al., 2011;王平等, 2017).所以, PM2.5日均值浓度序列可以看作是低频部分和高频部分的叠加, 其中, 低频部分是基础部分, 也可以看作是该地区PM2.5的本底值, 高频部分可以看作是PM2.5受外界影响产生的增加值, 本方法的预测就是利用小波分解把各个部分分解出来, 然后进行单独分析, 最后进行合成.图 6和图 7分别给出了训练数据集、测试数据集经小波分解后各层子波信号序列.其中, A3表示原始序列经分解后的低频部分(即趋势部分), 可以看出该曲线已经较光滑, 保持了原PM2.5观测序列的曲线形状, 并具有年周期性, 代表了天气变化模式、污染源排放等长期趋势.D3、D2和D1分别表示序列在各层的高频部分(即细节部分), D3、D2又称周期部分, 代表了光照、温度、平均风速、污染源等具有周期性因素的影响;D1则主要表现为随机分量, 包含了局部小尺度过程的随机扰动(如污染源的随机排放等).
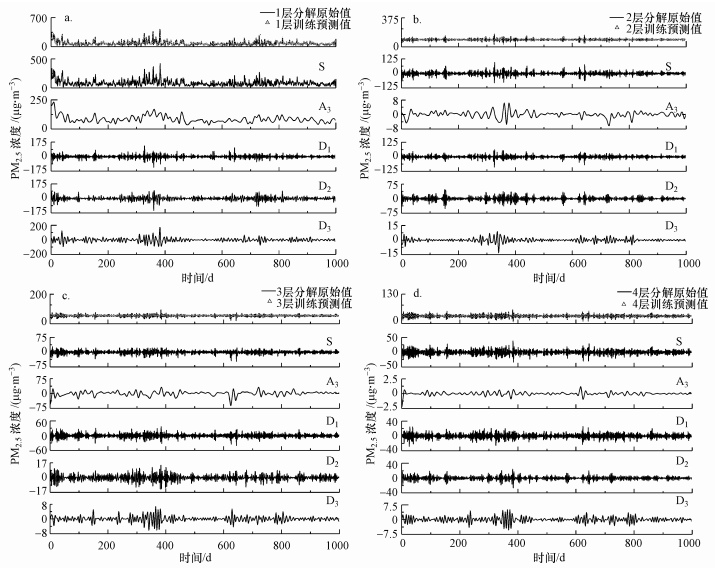 |
| 图 5 基于训练数据集的AMLRC-WLSSVM模型训练结果(4层) (a. 1LRC-WLSSVR小波分解与模型训练结果, b. 2LRC-WLSSVR小波分解与模型训练结果, c. 3LRC-WLSSVR小波分解与模型训练结果, d. 4LRC-WLSSVR小波分解与模型训练结果) Fig. 5 The training results of AMLRC-WLSSVM model based on training data sets (4 layers) |
 |
| 图 6 基于测试数据集的AMLRC-WLSSVR模型预测结果(4层) (a.训练数据预测对比, b.测试数据预测对比, c. 1LRC-WLSSVR小波分解与模型预测结果, d. 2LRC-WLSSVR小波分解与模型预测结果, e. 3LRC-WLSSVR小波分解与模型预测结果, f. 4LRC-WLSSVR小波分解与模型预测结果) Fig. 6 The AMLRC-WLSSVR model prediction results based on test data sets (4 layers) |
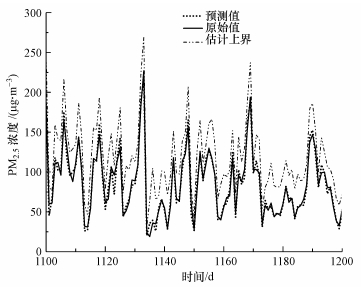 |
| 图 7 济南市科干所PM2.5总体训练预测曲线区间图示(包含97%置信上界) Fig. 7 The interval diagram of the PM2.5 general training prediction curve (including the 97% confidence upper bound) of Kegansuo monitoring station in Jinan |
由图 6可知, 在训练数据集和测试数据集中, 高频部分与原始数据基本保持一致, 低频部分与原始数据差别较大, 表明该方法能够很好地表征PM2.5的随机变化特征, 也说明PM2.5日均值浓度受随机影响较大.低频部分(A3)主要表征PM2.5的变化趋势及变化规律, 低频部分(A3)呈现出一定的周期性, 且2013-2017年波动性存在逐年减小的趋势.可见近年来采取的一系列环保措施取得了一定的效果, 但还是会存在较大波动的现象, 即PM2.5浓度较高(重污染天气情况).周期性部分(D3、D2)所占比重较大.
3.3 基于WD-AMLRC-WLSSVR的预测结果分析将A3、D1、D2、D3的预测序列通过小波相间重构即得到PM2.5日均值的预测值.本文采用平均绝对误差(MAE)、均方根误差(RMSE)、中值绝对误差(MEDAE)、R2作为评价指标对模型预测结果进行评价, 表 1给出了WLSSVR和AMLRC-WLSSVR模型PM2.5日均值浓度预测相关评价指标的对比值.可以看出, 无论是训练集还是测试集, AMLRC-WLSSVR的预测结果均优于WLSSVR的预测结果, 说明该模型对于PM2.5浓度的短期预测是有效的.这主要是因为AMLRC-WLSSVR能够在预测过程中产生的误差累积序列进行二次SVR预测的基础上, 实现对初始预测误差的自适应修正, 具有较强的鲁棒性.
| 表 1 基于济南市科干所PM2.5数据集的AMLRC-WLSSVR模型性能分析 Table 1 The performance analysis of AMLRC-WLSSVR model based on PM2.5 data set of Kegansuo monitoring station in Jinan |
图 7给出了包括预测值及其置信区间上界与验证值(准确值)的对比情况, 直接证明了WD-AMLRC-WLSSVR具有较佳的预测性能.特别是对于突起(PM2.5浓度波动较大处)的追踪性更强, 说明该方法可以应用于重污染天气的预警.然而由于预测本身的不确定性, 导致预测结果不会是一个精确的数值, 考虑到预测的目的是为污染预警做准备, 故可统计得到在一定概率下的区间值, 只需得到区间的上界值(阈值)即可实现污染预警.所以, 对预测残差做方差估计得到预测结果97%置信区间的上界, 当预测结果的区间上界值接近或者达到甚至超过警戒值时, 可以提前做出预警, 采取相关措施, 避免更加严重的环境事件发生.如图 7所示, 预测值和准确值之间有一定偏差, 但大部分都在置信区间上界以下, 有效避免了单纯点估计的不确定性问题.
4 结论(Conclusions)1) 采用小波分解与最小二乘支持向量回归相结合的方法对PM2.5的时间序列数据进行分析.通过小波分解, 将一维数据分解得到高维信息, 很好地表征了时间序列的周期性、趋势性及随机性特征.结合自适应多级残差修正与最小二乘支持向量回归对PM2.5进行建模预测, 试验结果表明, AMLRC-WLSSVR对PM2.5日均值浓度的时间序列有很好的预测精度, 特别是对短期预测有较好的效果, 符合实际预测需要.
2) 通过AMLRC-WLSSVR与WLSSVR的预测结果对比发现, AMLRC-WLSSVR各项指标均优于WLSSVR, 该方法能够对预测误差进行自适应修正, 提高预测精度, 特别是对于浓度变化较大的点预测精度较高, 表现出良好的泛化性.
3) 本文提出一种利用方差估计得到预测值区间估计上界(给出97%置信区间的上界)的方法, 该方法有效避免了单纯点估计不确定性的问题, 特别是预测精度不高时, 在当前PM2.5浓度预测较困难的情况下, 该方法提供了一种新思路, 能够为制定合理的预警方案提供参考.
蔡刚. 2012. 环境空气中PM2.5的测定方法[J]. 甘肃科技, 2012, 28(12): 45–46.
DOI:10.3969/j.issn.1000-0952.2012.12.019 |
陈国初, 王鹏, 徐玉法, 等. 2011. 基于小波分解的风电场短期功率混合预测模型[J]. 山海电机学院学报, 2011, 14(3): 163–168.
|
陈倩倩. 2013. 基于岩土工程信号特征的小波基构造及其算法与实现研究[D]. 长沙: 长沙理工大学
|
崔治, 彭楚武, 崔宪普. 2013. 光伏并网扰动检测中基于局部模极大值的小波选取[J]. 计算技术与自动化, 2013, 32(3): 89–92.
|
Jazebi S, Vahidi B, Jannati M. 2011. A novel application of waveletbased SVM to transient phenomena identification of power transformers[J]. Energy Conversion and Management, 52(2): 1354–1363.
DOI:10.1016/j.enconman.2010.09.033
|
李翔. 2013. 基于GAB和模糊BP神经网络的空气质量预测[J]. 华中科技大学学报(自然科学版), 2013, 41(增刊Ⅰ): 63–66.
|
李祥, 彭玲, 邵静, 等. 2016. 基于小波分解和ARMA模型的空气污染预报研究[J]. 环境工程, 2016, 34(8): 110–114.
|
刘小兵. 2016. 基于支持向量回归机的PM2. 5浓度预测模型分析与研究[D]. 成都: 西南财经大学
|
刘伟, 李春青, 张艳芬. 2013. 基于小波分解和最小二乘支持向量机的COD预测[J]. 微电子学与计算机, 2013, 30(4): 26–29.
|
龚海鹏. 2008. 小波变换在转子故障诊断中若干问题的研究[D]. 上海: 上海交通大学
|
沈路路, 王聿绚, 段雷. 2011. 神经网络模型在O3浓度预测中的应用[J]. 环境科学, 2011, 32(8): 2231–2235.
|
石亚欣. 2014. 基于时间序列的WDLSSVM的风速周期预测模型研究[J]. 电力科学与工程, 2014(2): 41–45.
|
司志娟, 孙宝盛, 李小芳. 2013. 基于改进型灰色神经网络组合模型的空气质量预测[J]. 环境工程学报, 2013, 7(9): 3543–3547.
|
宋宇辰, 甄莎. 2013. BP神经网络和时间序列模型在包头市空气质量预测中的应用[J]. 干旱区资源与环境, 2013, 27(7): 65–70.
|
谭德彪. 2003. 城市环境空气质量预报模式的研究[A]//四川省环境科学学会2003年学术年会论文集[C]. 成都: 四川省环境科学学会. 172-175
|
向昌盛, 周子英. 2010. ARIMA与SVM组合模型在害虫预测中的应用[J]. 昆虫学报, 2010, 53(9): 1055–1060.
|
谢屹鹏, 汪西莉. 2010. 基于GA-LSSVR的渭河水质参数遥感反演研究[J]. 遥感技术与应用, 2010, 25(2): 257–262.
DOI:10.11873/j.issn.1004-0323.2010.2.257 |
谢涛, 姚新, 孙世友. 2011. 基于GIS的空气质量多模式集合预报系统[J]. 地理信息世界, 2011, 9(1): 11–15.
|
喻彩丽. 2016. 基于空气质量时间序列分析的预测模型设计与应用[D]. 银川: 宁夏大学
|
王平, 张红, 秦作栋, 等. 2017. 基于wavelet_SVM的PM10浓度时序数据预测[J]. 环境科学, 2017, 38(8): 3153–3161.
|
翁剑桥. 2010. 济南市城市大气环境质量评价与污染特征研究[D]. 济南: 山东大学
|
张海艳. 2011. 基于自适应概率神经网络的农作物虫情预测研究[D]. 兰州: 兰州交通大学
|
朱亚杰, 李琦, 等. 2016. 基于支持向量回归的PM2.5浓度实时预报[J]. 测绘科学, 2016, 41(1): 12–18.
|
 2018, Vol. 38
2018, Vol. 38


