化学条件和絮凝动力学条件是絮凝科学的两大支柱.其中, 絮凝动力学研究混凝的速度问题, 只有具有一定速度的絮凝过程才能满足水处理对出水水量的要求, 因而才具有实际意义(常青, 2011).因此, 水力条件对絮凝具有十分重要的影响.目前我国各类高效水处理构筑物中水流条件一般为湍流, 而有关湍流絮凝机理和动力学本质还不甚明了, 仍需进行深入研究.
湍流是一种极不规则的流动现象, 其不规则性不仅表现在速度、压强等流动物理量在时空中的不规则性, 还表现在它的不重复性, 除此之外, 湍流还表现出多尺度性和复杂的非线性输运(张兆顺等, 2005).因此, 湍流的测量也是一大难题.近些年兴起的粒子图像速度场仪(Particle Image Velocimetry, PIV)是超出单空间点的测量技术, 能瞬间测量几千乃至上万个点的速度, 从而提供丰富的流动空间结构信息.PIV测量技术不仅能够无扰地对流场进行测量, 且能获得测量区域内的瞬时速度场, 已被广泛地应用到湍流测量中(饶麒等, 2004).
Taylor-Couette是一种传统涡发生器, 它由两个同心圆筒构成, 两圆筒之间的流体在内筒转动、外筒固定的条件下会经历一系列复杂多变的湍流(涡)流动形态(Soon et al., 2007).与传统的机械搅拌反应器内接触式搅拌混合方式不同, Taylor-Couette反应器环隙内产生的主要是涡流场, 通过控制其发生条件(也就是控制内筒转速), 环隙内涡流场及其形态特征有很好的重现性.因此, 可以根据需要控制Taylor-Couette反应器重现并获取到各种目标涡流场, 并利用Taylor-Couette反应器进行絮凝反应, 研究混凝过程中流场湍流动能及其耗散率与流场混合及絮凝效能的关系.
对Taylor-Couette反应器的研究此消彼长.张长高(2001)、刘难生等(2002)均对湍流Taylor-Couette流进行了研究, 毛玉红等(2015a, 2015b;2014)利用PIV对Taylor-Couette流中不同涡形态下的混凝效果进行了研究.这些研究多是对Taylor-Couette进行的二维PIV测量, 无法直接从测量软件中输出湍动动能及其耗散率.本文拟用大涡PIV方法对Taylor-Couette流进行湍动能耗散率的估算, 且将这些指标与混凝过程絮体形貌变化和浊度去除率进行相关性分析, 探究湍动能及湍动能耗散率对絮凝的影响.从而寻找提高絮凝效能的途径并为优化絮凝工艺提供理论依据, 以期为实际工程的设计和优化提供指导.
2 装置与实验(Installation and experiment)Taylor-Couette涡发生器由本实验室自制, 外筒固定, 内筒旋转.其中, 外筒由透明有机玻璃制成, 外筒内径r0=50 mm;内筒由不锈钢制成, 内筒外径ri=37.5 mm;环隙宽度d=r0-ri=12.5 mm, 筒高L=440 mm, 内外筒半径比η=ri/r0=0.75.内筒由ABB变频器控制电动机驱动, 从而保证得到目标转速.为了防止光学畸变, 在筒体外加入了相同材质的方形水槽, 以进行光路补偿, 减少光折射, 从而得到真实的流场信息.试验系统如图 1所示, 图中竖向阴影部分为环隙流场子午面示意.子午面上沿筒高方向为轴向, 沿环隙半径方向为径向, 子午面上任意高度上的环隙半径为径线.
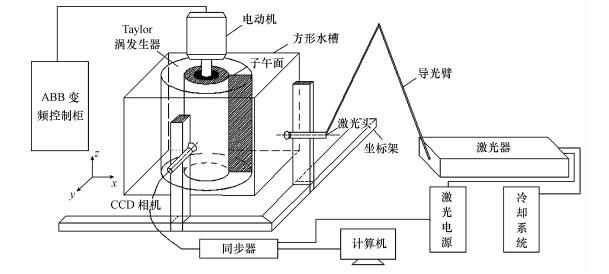 |
| 图 1 实验装置系统示意图 Fig. 1 Experimental device system |
本实验所采用的PIV系统为丹麦Dantec公司的产品, 包括双脉冲Nd:YAG激光器、同步器(HUB)、高速Flowsense 2M CCD相机及PIV软件系统等.图像处理过程通过adapt-correlation进行自适应互相关得到瞬时速度矢量场, 采用查问区为32×32像素, 50%重叠率.
本次试验在装置中先投加示踪粒子, 通过PIV对每个转速各拍摄50对图像, 从而得出单纯水力条件下的流场信息;另外, 再用高岭土配置浊度为100 NTU左右的水样, 分别采用PAC、FeCl3、PFS等絮凝剂在相应转速下进行絮凝实验.以500 r·min-1的内筒转速快搅2 min, 使絮凝剂与水样充分混合, 接着以不同的目标转速缓慢旋转10 min, 进行絮凝反应;对每个转速, 在絮凝反应进行到第2、4、6、8、10 min时分别启动PIV拍摄一组粒子图像.最后静置沉降10 min, 在水面下210 mm处取样测定剩余浊度.
3 计算方法(Calculation method) 3.1 旋转雷诺数为方便实验操作, 旋转雷诺数Re可表示为转速n的表达式:
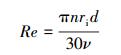
|
(1) |
式中, n 为内筒转速(r·min-1), ri为内筒半径(m), d=r0-ri为环隙的宽度(m), ν为流体的运动粘度(m2·s-1).由式(1)可知, 当环隙间的流体确定以后, 流体的运动粘度ν是定值, 旋转雷诺数只与内筒转速和内外筒半径的大小有关.当内外筒半径固定以后, 雷诺数只与内筒转速有关.因此, 在几何条件固定的情况下, 通过控制内筒转速就可以获得流场需要的雷诺数, 实现对不同雷诺数下的涡流场的重现.
3.2 输出PIV流场的湍流动能湍流动能的表达式为:

|
(2) |
式中, u′r、u′z、u′θ分别为流场中径向、轴向和切向的脉动速度, 在PIV输出二维数据的基础上, 运用局部各向同性假设即可得出其切向速度为:
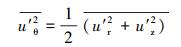
|
(3) |
因此, 湍动能的计算式为:
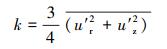
|
(4) |
在PIV软件中, 对各转速下PIV所测瞬时流场, 运用统计平均命令可得到时均流场, 任意瞬时流场与统计平均流场中各点速度之差即为脉动速度.根据式(4)即可利用PIV所测流场的径向和轴向脉动速度计算输出该流场的湍流动能.
3.3 湍流动能耗散率与Kolmogorov尺度实验中用于带动内筒转动的动力装置为三相异步电机, 其运行功率公式为:

|
(5) |
式中, P为电动机运行功率(W), U为电动机电压(V), I为电动机线电流(A), cosφ为功率因数, 由电动机铭牌中查得cosφ=0.76.
单位质量流体的输入功率也即平均湍动能耗散率ε为:
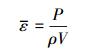
|
(6) |
式中, ρ为工作介质水的密度, V为Taylor-Couette涡发生器内流体体积, 则平均Kolmogorov尺度为:
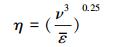
|
(7) |
通过式(7)可得出各转速对应流场的Kolmogorov尺度, 且转速越高, 平均Kolmogorov尺度越小.从理论上说, PIV所采用的查问区尺度, 即PIV的空间分辨率, 要接近于Kolmogorov尺度, 才能用直接测量法得到湍流动能耗散率.但一般PIV的查问区尺度均大于湍流场中的最小涡旋尺度.例如, 内筒转速为50 r·min-1时, 通过ABB变频器可读出电动机线电流为0.6 A, 此时算得平均Kolmogorov尺度为0.01985 mm.而PIV的查问区为32×32像素, 其长度为1.06941 mm, 是Kolmogorov尺度的54倍.目前的PIV达不到如此高的测量分辨率, 不能进行直接测量, 也不能直接在Kolmogorov尺度上计算ε.只能采用大涡PIV方法估算湍流动能耗散率.
3.4 大涡PIV方法在湍流中, 湍动能产生于大尺度脉动, 耗散于Kolmogorov微尺度.而介于两种尺度的惯性子区内湍动能既不产生也不耗散, 仅起传递作用, 传递的能量就等于在Kolomogorov尺度上耗散的能量.因此, 计算湍流动能耗散率只需计算出在惯性子区内传递的湍流动能(张兆顺等, 2008).更重要的是, 惯性子区尺度比Kolomogorov尺度大得多, 用大涡PIV方法计算出在惯性子区内传递的湍动能, 就可大大降低对测量分辨率的要求(江涵等, 2010).
大涡模拟即用位于惯性子区内的截断尺度对N-S方程进行过滤, 得到大涡控制方程, 从而直接计算可解尺度上的脉动, 对不可解尺度上的脉动用亚格子模型求解.将各瞬时量分解为可解尺度上的量(也就是PIV测得的速度)和不可解尺度上的量(用亚格子模型求解)即可对目标量进行进一步计算.详细处理方法与计算公式见参考文献(刘心洪等, 2008).计算中Smagorinsky常数值在0.16~0.18之间, 本次试验取CS=0.16.
3.5 数值模拟将整个反应器环间隙均作为计算域, Taylor湍流的控制方程为三维不可压缩流动的N-S方程和连续性方程, 其无量纲形式为:
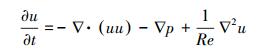
|
(8) |
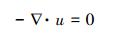
|
(9) |
本文中数值模拟采用柱坐标系, 故速度u分量ur、uθ、uz分别代表径向速度、切向速度和轴向速度, 在柱坐标中切向速度沿逆时针方向为正, p为压强, Re为旋转雷诺数.
采用Gambit建立计算模型, 模型大小与实际反应器尺寸一致.利用Fluent6.3, 基于有限体积法对此模型进行模拟.压力-速度耦合采用SIMPLE格式, 选择κ-ε双方程标准湍流模型, 二阶迎风离散格式.κ-ε双方程标准湍流模型具有良好的收敛性, 并得到了广泛的检验与成功运用(马婷婷等, 2014), 二阶迎风离散格式具有绝对稳定、精度较一阶迎风高等特点(阎超等, 2011).设定外筒为固定边壁, 内筒旋转, 上下底面设置为自由液面, 设置流场特性残差曲线监视后, 开始数值模拟, 当残差曲线迭代收敛时结束.根据流动的对称性, 即可输出对称的环隙速度场.
4 结果与讨论(Results and discussion) 4.1 大涡PIV方法与数值模拟方法对比分析为验证大涡PIV法, 输出数值模拟中各转速下的流场子午面上各点湍动能与湍动能耗散率, 并对环隙子午面上流体的湍动能与湍动能耗散率取平均值.将两种方法的计算结果进行比较, 选取几个目标转速下的值列于表 1中.
| 表 1 不同方法获得的平均湍动能与湍动能耗散率 Table 1 Mean value of the turbulent kinetic energy and dissipation rate at different rotation speeds |
通过横向比较可以发现, 湍动能与湍动能耗散率整体上随着转速的增加而增大(图 2).但在较小转速情况, 利用大涡PIV方法所计算出的湍动能与湍动能耗散率大小出现不同程度的紊乱, 例如, 在40 r·min-1时所计算出的湍动能值比50 r·min-1时要大.通过纵向对比发现, 在较低转速下, 两种方法所算出的结果相差较大, 甚至在有些转速下相差一个数量级(如40、50 r·min-1).不过随着转速的增加两种方法所得结果的数值差距逐渐减小, 直至最后两者之间数值相近.
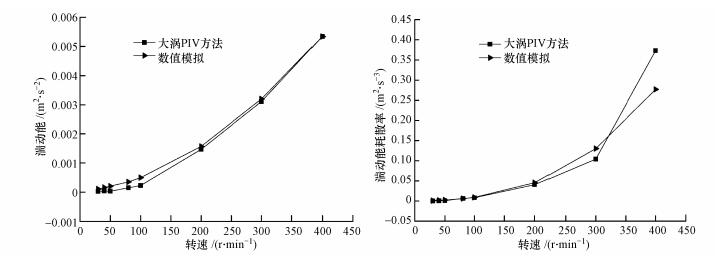 |
| 图 2 不同方法获得的平均湍动能与湍动能耗散率比较 Fig. 2 Comparison between the value obtained with different methods |
在较低转速下大涡PIV计算结果与实际情况有较大的差异, 这是由于大涡PIV方法计算湍动能与湍动能耗散率的前提是局部各向均匀同性假设, 当转速较低时, 流场不能达到各向均匀同性, 其实际情况与假设条件相差较大导致.当转速逐渐增大, 实际情况逐渐与假设条件相接近, 数值模拟与大涡PIV的计算数值也非常接近.因此, 大涡PIV只适用于雷诺数较大的情况.对转速较小, 即雷诺数较低的流场情况, 不宜采用大涡PIV方法计算湍动能与湍动能耗散率.
4.2 混凝过程流场湍流动能图 3为不同转速下的混凝流场湍流动能分布情况.由图可以发现, 速度矢量场与湍动能的分布密切相关.当n=50 r·min-1时, 涡形态完整, 此时湍动能呈环状分布, 在涡外侧较大, 且越靠近涡心, 湍动能越小.当n=80 r·min-1时, 湍动能虽仍呈环状分布, 但明显变得杂乱, 且内侧湍动能比外侧小.在n=100 r·min-1时, 湍动能在各区域之间数值大小上的差距相对较小;但转速达到200 r·min-1时, 湍动能在不同区域的分布差距变大, 数值大小差距较大, 且速度矢量图越混乱湍动能越大.在转速为300 r·min-1时, 各处湍动能开始趋于相同, 但局部区域依然可以看出和周围有较大差距.当转速达到400 r·min-1时, 这种差距开始变小, 湍动能在空间上的分布几乎各处相同.此时流场中已经没有完整的大涡存在, 整个流场变得紊乱无序, 各处的湍动能分布趋于相同.
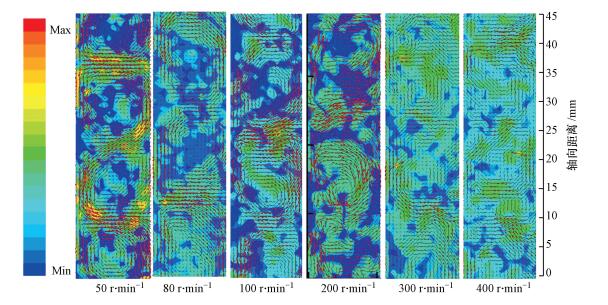 |
| 图 3 不同流场湍流动能分布 Fig. 3 Distribution of turbulent kinetic energy in the flow field at different rotation speeds |
为进一步获取湍动能分布特征, 对通过涡心处环隙径线上分布的湍动能进行无因次化(k/v2, k为湍动能, v为内筒壁处速度), 将计算处理结果列于图 4中.由图可知, 当转速为50、80 r·min-1时, 湍动能值在边壁处较大, 在环隙中数值相对较小且较为平稳.这也与湍动能云图上结果相符合, 即在50、80 r·min-1时呈环状分布:四周大, 涡心处小;当转速为100、200 r·min-1时, 湍动能分布波动较剧烈, 波动幅度较大, 说明在此时湍动能在环隙中的分布已经紊乱;当转速为300 r·min-1时, 湍动能的波动幅度相较100、200 r·min-1时明显减小;当转速为400 r·min-1时, 湍动能分布平缓, 波动范围很小, 几乎类似于直线, 相当于此时径线上各点的湍动能值已经趋于相同.综上, 通过对各转速下径线上湍动能的分布情况的分析可知, 径线上随转速的分布特征与湍动能云图的分布特征相吻合, 且随着转速的增加流场中各点的湍动能趋于各处相同.
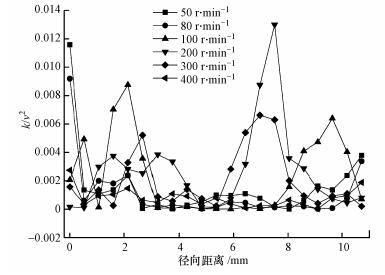 |
| 图 4 不同流场子午面径线上的湍动能分布趋势 Fig. 4 Distribution tendency of turbulent kinetic energy on radial lines of meridianal plane in different flow field |
综上所述, 随着转速的增加, 湍动能在环隙流场中的分布趋势由规律有序到紊乱最终趋于各处均匀一致.
4.3 混凝过程流场湍动能耗散率图 5为不同转速下的混凝流场湍动能耗散率分布情况.与图 3对比发现, 当转速为50、80 r·min-1时, 湍动能耗散率与湍动能的分布较为相似, 在此转速下湍动能耗散率大致呈环状分布, 涡心处湍动能耗散率最小, 涡外侧较大.当转速为100、200 r·min-1时, 湍动耗散率依然呈环状分布, 但在此转速下湍动能耗散率与湍动能的分布状况有较大差异.当转速增加到300、400 r·min-1时, 湍动能与湍动能耗散率的分布再次趋于一致.在此转速下湍动能耗散率在整个流场中的分布趋于各处相同.因此, 通过上述分析可知湍动能耗散率随着转速的变化趋势与湍动能较为相似, 均为随着转速的增加, 其在空间上的分布均由规律到混乱最终趋于各处相同.
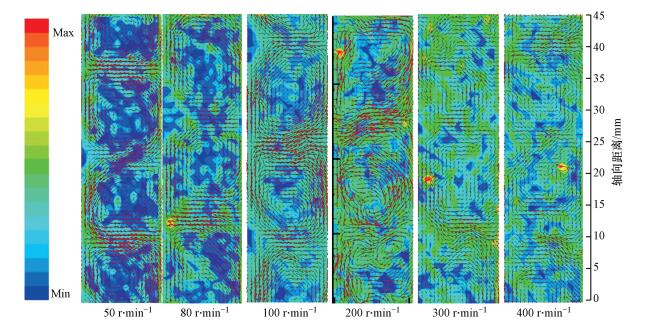 |
| 图 5 不同流场湍动能耗散率分布 Fig. 5 Distribution of turbulence kinetic energy dissipation rate in the flow field at different rotation speeds |
由式(4)可知, 湍动能的大小变化状况与脉动速度的变化密切相关, 而湍动能耗散率的变化情况与应变变化率的平方有关.在转速为50、80 r·min-1时, 由矢量图可知此时涡形态完整, 流场相对稳定, 脉动速度与应变变化率的变化较小, 涡外围脉动速度与应变变化率相对较大, 涡心处较小.因此, 湍动能与湍动能耗散率均呈环状分布, 且在涡心处最小.当转速达到100、200 r·min-1时, 此时虽依然可以看出涡的存在, 但在此情况下涡的形态已变形, 流场趋于紊乱.故此时脉动速度变化较大, 应变变化率变化较小.因此, 湍动能的分布已经杂乱无序, 而湍动能耗散率依然呈环状分布.当转速进一步增加到300、400 r·min-1时, 流场已经处于完全湍流状态, 各类指标趋于各向均匀分布.
对通过涡心处径线上的湍动能耗散率进行无因次化后, 得到其分布图 6(ε/(D2N3), 其中, D为内筒直径, N为内筒转速;计算时涉及到的所有参数均统一换算为国际单位).由图可知, 湍动能耗散率与湍动能在径线上的分布较为相似, 当转速达到400 r·min-1时, 在径线上各点的湍动能耗散率已趋于各处相同.综上, 通过对各转速下径线上湍动能耗散率分布情况的分析发现, 径线上随转速的分布特征与湍动能耗散率云图的分布特征相吻合, 且随着转速的增加流场中各点的湍动能已趋于各处相同.
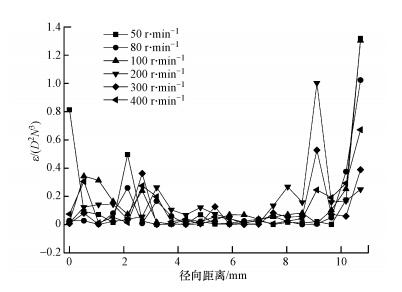 |
| 图 6 不同流场子午面径线上的湍动能耗散率分布趋势 Fig. 6 Distribution tendency of turbulence kinetic energy dissipation rate on radial lines of meridianal plane in different flow field |
综上所述, 随着转速由低到高, 湍动能在环隙流场中的分布趋势由规律有序到紊乱最终趋于各处均匀一致.在高雷诺数下, 湍动能与湍动能耗散率在流场中的分布趋于各处相同.这也与张兆顺等(2002)的观点一致, 即湍流的大涡结构对于湍流生成与发展有主宰作用, 抑制和消除大涡结构可能会抑制整体的湍流强度, 甚至会使流动层流化, 而失去了一定的湍流强度的流场其混凝效果并不好.
4.4 混凝过程流场中湍动能与絮体形态相关性PIV系统的高速CCD能将絮凝剂与高岭土在不同条件下的混凝过程中形成的絮体作为粒子图像而记录下来(毛玉红等, 2014), 等比例截取PIV测量图的1/16作为絮体图片, 按絮凝时间先后横向排列, 以及转速从小到大排列, 即可组成可显示絮体颗粒大小、粒径分布变化等形态特征的图谱, 图谱中每一小幅图与PIV原图均有相同比例, 相同的絮体特征.抽取絮体图谱中目标转速下各时刻粒子图像组成图 7.对每一个混凝过程, PIV均连续拍摄50对照片.对这50对照片进行全面分析, 再筛选出具有共性且最具代表性的图片, 以反映其共性特征, 避免出现随机性与不确定性导致的单一特征.由图可知, 当转速为50、80 r·min-1时, 絮体粒径随着絮凝时间由小变大, 絮体颗粒数量随着时间由多变少, 但对比这两个转速可以发现, 50 r·min-1时出现大絮体的时间比80 r·min-1要早, 且在絮凝10 min时几乎没有小絮体颗粒;同时在相同的絮凝时间内, 50 r·min-1时大絮体要比80 r·min-1时要多, 絮体粒子数量恰好相反, 80 r·min-1时的粒子数量要比50 r·min-1时要多, 且大多数为小絮体.当转速为100、200 r·min-1时, 絮体明显变小, 数量增多, 出现絮体破碎现象.特别是转速为200 r·min-1时, 整个絮凝过程中几乎全为小絮体, 因为所生成的稍微大一点的絮体明显地被破碎为更加细小的絮体.当转速达到300、400 r·min-1后, 在整个絮凝过程中不能产生大絮体, 悬浮物颗粒大小几乎没有变化, 且随着絮凝时间的推移悬浮颗粒反而被破碎得更细小.
 |
| 图 7 不同转速流场絮体颗粒变化情况 Fig. 7 Variation of flocs in the flow field at different rotation speeds n is the rotation speed of the inner cylinder |
综上所述, 混凝过程中所产生絮体颗粒粒径大小与分布应该与相应流场的湍动能及其耗散率分布存在一定的相关关系.图 8为用大涡PIV方法在不同转速下得到的平均湍动能和湍动能耗散率及相应流场条件下的浊度去除率关系.由图可知, 随着转速的增加, 湍动能与湍动能耗散率由缓慢逐渐递增变为剧烈增大, 而浊度去除率逐渐降低, 且当湍动能增加到一定程度时, 浊度去除率维持在一个非常低的水平, 不再发生变化.
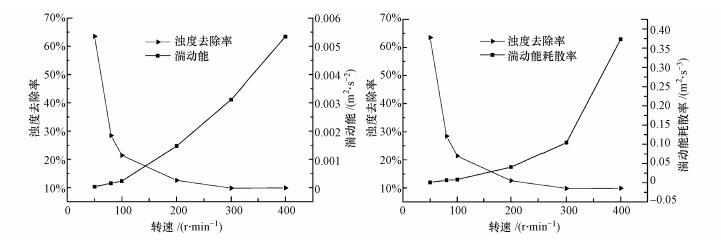 |
| 图 8 不同流场下的絮凝效果和湍动能、湍动能耗散率 Fig. 8 Comparison between the flocculation efficiency, turbulent kinetic energy and turbulence kinetic energy dissipation rate |
综合图 2~8与表 1可得, 转速处于50~100 r·min-1时, 各转速下的湍动能、湍动能耗散率均处于同一数量级.在此转速范围内, 流场湍动能与湍动能耗散率的变化不大, 且存在分布不均匀现象.当转速为50 r·min-1时, 流场中涡间的湍动能与湍动能耗散率分布较规律, 产生絮体较大, 数量相对较少, 浊度去除率较高;当转速达到80 r·min-1时, 流场中涡间的湍动能与湍动能耗散率分布开始变得杂乱, 此时虽有大絮体, 但较松散, 相应的浊度去除率有所下降;转速达到100 r·min-1时, 流场中涡间的湍动能分布已经紊乱, 流场中没有较大絮体存在, 浊度去除率降低.当转速处于100~200 r·min-1时, 湍动能分布有些混乱, 且与湍动能耗散率的分布状况有较大差异, 但湍动能耗散率还呈环状分布.湍动能与湍动能耗散率的数值大小也相差一个数量级.由图 8可知, 100 r·min-1时对应的浊度去除率明显要比200 r·min-1时高.当转速大于200 r·min-1后, 湍动能与湍动能耗散率值增加过大, 絮体承受过大的脉动速度与剪切力, 导致出现絮体破碎现象, 使絮体几乎不会聚集长大, 浊度去除率维持在一个较低的水平, 且不再随转速升高而发生变化.
综上所述, 湍动能与湍动能耗散率的大小及其在流场中的分布情况, 对絮体大小和浊度去除率均有影响.混凝效果不仅与湍动能及其耗散率的分布趋势有关, 还与其值的大小有关.在空间分布趋势较为规律且数值较小的混凝过程中, 絮凝效果较好;在空间上分布趋势规律, 但数值较大时, 虽出现大絮体但絮体较松散, 絮凝效果不太好;在空间上分布趋势混乱, 且数值较大时, 出现絮体破碎现象, 絮体一般为雾状小颗粒, 絮凝效果极差.而当转速大于200 r·min-1以后, 湍动能与湍动能耗散率值过大, 絮体承受过大的脉动速度与剪切力冲击而过分破碎, 导致絮体几乎不会聚集长大, 浊度去除率只能在一个较低的水平, 几乎不再随转速升高而发生变化.
5 结论(Conclusions)1) 大涡PIV方法与数值模拟在雷诺数较高的情况下有较好的一致性, 且雷诺数越高其一致性越好.因此, 大涡PIV法只适用于雷诺数较大的情况, 雷诺数较低情况(低于2500)不宜采用.
2) 随着雷诺数的增大, 湍动能与湍动能耗散率在流场中的分布趋势由规律有序到紊乱最终趋于各处均匀一致.而混凝过程中湍动能与湍动能耗散率的数值大小及其在流场中的空间分布情况, 均对产生絮体的形态和浊度去除率有较大影响.
3) 在湍动能与湍动能耗散率的空间分布趋势较为规律且数值适合的混凝过程中, 絮体较大且絮凝效果较好;当空间分布趋势较为规律, 但其数值较大时, 虽能产生大絮体但较松散, 絮凝效果不好;当湍动能与湍动能耗散率值过大时, 絮体受到过分冲击而破碎, 不会聚集长大, 导致絮凝效果较差.
常青. 2011. 水处理絮凝学(第2版)[M]. 北京: 化学工业出版社.
|
江涵, 刘心洪, 黄雄斌. 2010. 用2D-PIV方法研究固-液方形搅拌槽内液相湍流[J]. 过程工程学报, 2010, 10(1): 1–9.
|
刘难生, 董宇红, 陆夕云, 等. 2002. 旋转同心圆筒间Couette-Taylor流动的数值模拟[J]. 中国科学技术大学学报, 2002, 32(1): 91–97.
|
刘心洪, 闵健, 潘春妹, 等. 2008. 采用大涡PIV方法研究搅拌槽内湍流动能耗散率[J]. 过程工程学报, 2008, 8(3): 425–431.
|
马婷婷, 孙津生, 王运东. 2014. 混合澄清槽数值模拟与实验研究进展[J]. 化工进展, 2014, 33(4): 795–802.
|
毛玉红, 常青, 曾立云. 2014. 混凝过程中流场结构的PIV测量与表征[J]. 环境科学学报, 2014, 34(5): 1206–1211.
|
毛玉红, 冯俊杰, 常青, 等. 2015a. 壳聚糖助凝对PAC混凝过程的影响[J]. 中国环境科学, 2015a, 35(4): 1096–1102.
|
毛玉红, 冯俊杰, 常青, 等. 2015b. 不同涡流场形态下混凝效能研究[J]. 环境科学学报, 2015b, 35(9): 2826–2832.
|
Soon M, Wang L, Fox R O, et al. 2007. Population balance modeling of aggregation and breakage in turbulent Taylor-Couette flow[J]. Journal of Colloid and Interface Science, 307(2): 433–446.
DOI:10.1016/j.jcis.2006.12.016
|
阎超, 于剑, 徐晶磊, 等. 2011. CFD模拟方法的发展成就与展望[J]. 力学进展, 2011, 41(5): 562–589.
DOI:10.6052/1000-0992-2011-5-lxjzJ2010-082 |
张长高. 2001. 论紊流Couette流[J]. 河海大学学报, 2001, 29(1): 70–76.
|
张兆顺, 崔桂香, 许春晓. 2002. 走近湍流[J]. 力学与实践, 2002, 24(1): 1–8.
|
张兆顺, 崔桂香, 许春晓. 2005. 湍流理论与模拟[M]. 北京: 清华大学出版社.
|
张兆顺, 崔桂香, 许春晓. 2008. 湍流大涡数值模拟的理论和应用[M]. 北京: 清华大学出版社.
|
 2018, Vol. 38
2018, Vol. 38


