近几年来, 雾霾天气已经成为一种常态, 严重危害到人类的生理和心理健康, 此外, 雾霾天气对于各行各业都带来了不同程度的影响.对于处于雾霾高发区的京津冀地区, 雾霾带来的影响更是愈演愈烈.除了城市自身污染源所造成的雾霾污染, 外部周边城市雾霾污染物区域输送所带来的影响也不容忽视.事实上在污染源相对稳定的情况下, 雾霾还受诸多外在因素的影响, 如地理位置、地形、风力、风向、气温等.Tobler(1970)的“地理学第一定律”也指出任何事物都相关, 相邻事物关系更紧密.
随着人们对于雾霾污染问题的关注加深, 关于雾霾问题的相关研究也不断增加, 部分学者对空气污染的区域性特点进行了研究.张志刚等(2004)使用二维欧拉统计模式对区域空气污染状况进行了模拟, 结果证明了大气污染是一个区域性环境问题.段玉森等(2008)以API指数作为评价指标, 利用经验正交函数EOF方法将全国47个重点环保城市分为10个区域, 分别代表不同的空气污染时空模态.王斌(2008)采用聚类分析和小波分析等方法通过分析空气污染指数(API)得到了中国空气污染的区域时空变化特征.以上研究都表明空气污染存在着一定的区域性这个特点, 目前针对PM2.5在区域内扩散传输方面的研究多采用以CAMx模型(薛文博等, 2014)、WRF-CHEM模型(Gao et al., 2016)、NAQPMS模型(Li et al., 2017)、CMAQ模型(黄晓波等, 2016)等为主的空气质量模型.但是利用空气质量模型进行模拟也存在一定的不足, 例如空气质量模型对于气象、污染源等基础数据质量要求非常苛刻.随着网络科学的蓬勃发展, PM2.5在区域内城市之间的传输可以通过区域城市网络的联通模型进行刻画.
复杂网络是具有自组织、自相似、吸引子、小世界、无标度中的部分或者全部性质的网络(郭世泽等, 2012).Watts和Strogatz(1998)提出的小世界模型以及Barabási和Albert(1999)提出的无标度网络模型掀起了研究复杂网络的热潮.时至今日, 复杂网络已经广泛应用于各个领域, 诸如军事、经济、通信、社会、工程技术和管理等(方锦清等, 2007).但是目前将复杂网络应用于环境科学方面, 特别是城市间雾霾污染的研究还较少.张晓勇等(2014)通过分析城市环境中水平距离、海拔、风力等因素的作用, 以复杂网络为基础构建了城市PM2.5区域性扩散的网络模型, 并根据实时监测数据对西安市PM2.5浓度进行预测.薛安等(2015)采用城市间PM2.5浓度相关性作为权重构造出了中国城市PM2.5加权网络, 分不同季节通过区域连片度和模块化Q函数对网络进行划分, 得到的划分结果与大气污染防治规定提出的“三区六群”范围大致相同.刘华军等(2017)运用社会网络分析方法刻画出京津冀、长三角、珠三角、成渝、长江中下游五大地区雾霾污染空间关联的网络结构特征.Jin等(2014)应用复杂网络中的GN算法研究了中国2005年至2014年PM2.5排放的局部空间自相关, 得出了在同一区域内省份间PM2.5的排放存在巨大的相互影响.事实上, 将网络分析应用于研究区域雾霾网络的优势在于能有效刻画出区域雾霾网络的一个相互作用的关系及相互作用强度的差异.同时, 网络分析方法相较于复杂的空气质量模型, 对前期数据的准备及后期数据的处理、分析的要求不高, 大大提升了研究效率, 降低了投入的人力和物力, 因此更具有推广性.
目前将复杂网络应用于雾霾污染方面的研究都是站在全局的角度, 研究整个中国的雾霾污染区域分布及区域间的相互影响, 鲜有研究局部区域内城市间雾霾污染的联系.事实上, 雾霾污染在区域内城市与城市之间有着千丝万缕的联系, 图 1是基于京津冀13市PM2.5浓度相关系数矩阵, 通过R语言中chordDiagram函数所绘制出的城市间雾霾相关性复杂网络弦图.外圈的弧代表研究对象即京津冀13市, 弧越长则代表与其他城市间雾霾污染总相关性越高;内层的纽带代表两两研究对象的相关性, 若城市之间相关性不为0则相应城市间存在发出及汇入两条颜色的纽带;纽带的粗细反映的是相关性的大小, 纽带越粗则相关性越强.每个弧上都会有若干条不同颜色的纽带.以承德市为例, 承德所在弧上一共有26条纽带, 其中13条为发出纽带, 另外13条为汇入纽带, 发出纽带代表承德对其他城市及自身的相关性影响, 汇入纽带代表其他城市对承德的相关性影响.从图 1可以看出, 京津冀区域内城市之间的雾霾污染相关性错综复杂, 呈现出复杂网络的结构形态.
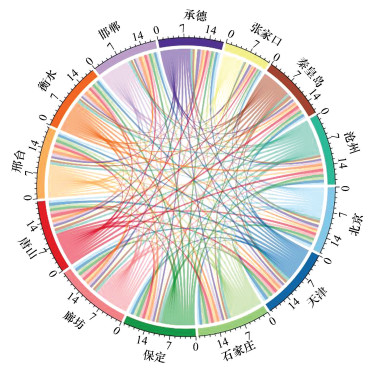 |
| 图 1 京津冀13市雾霾相关性复杂网络弦图 Fig. 1 Complex network chord diagram of haze correlation of 13 cities in Beijing-Tianjin-Hebei region |
因此本文基于复杂网络的相关内容, 将雾霾污染最为严重的京津冀地区的13个城市作为研究对象, 以城市为节点, 以城市间的PM2.5浓度的相关系数作为是否连边的衡量标准, 若连边则以相关系数与城市间最短距离的比值作为网络结构中边的权重, 构造出京津冀区域内城市间的雾霾污染加权网络, 在此基础上, 根据节点重要性评价方法得到京津冀区域内联系最为紧密的城市网络.
2 复杂网络中节点重要性度量方法(Measurement methods of node importance in complex networks)复杂网络是由大量的点和边所构成, 因此复杂网络中的一个图G可以定义为一个对(V, E), 记为G=(V, E), 其中V是节点的集合, E是边的集合(杨博等, 2009).而网络的邻接矩阵Α包含了网络的最基本拓扑性质, 描述了各个节点间的邻接关系.对于无向图中邻接矩阵Α的矩阵元aij的定义可以表示为(何大韧, 2009):
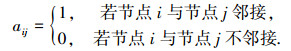
|
(1) |
而对于含权无向图中邻接矩阵Α′的矩阵元wij的定义可以表示为:

|
(2) |
接下来, 本文将介绍3种节点重要性度量方法.
2.1 度与集群系数节点i的度(Degree)定义为该节点的邻点数目(刘建国, 2013), 即与该节点相连的边数, 记为:
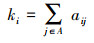
|
(3) |
式中, ki 为节点i的度, aij是邻接矩阵Α的矩阵元, 节点i与节点j相连时, aij=1;反之, aij=0.度能有效反映网络的局部特性, 在一个网络中, 度较大的节点在网络的局部中通常处于重要的地位.例如, 校长在学校范围内往往拥有更高的声望.
集群系数(Clustering coefficient)是描述网络中节点的邻点之间也互为邻点的比例, 即小集团结构的完美程度(何大韧, 2009).无权网络中节点i的集群系数也可以记为:
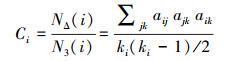
|
(4) |
式中, 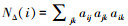
 |
| 图 2 三角形”与“三元组” Fig. 2 'Triangle' and 'Three tuple' |
图 2是一个含有i, j, k, m, n 5个节点的网络, 以节点i为例, 包含节点i一共有3个三角形(△ijk, △ikn, △imn)和6个“三元组”(jim, jin, kim, kij, kin, min).因此, 在这个无权网络中, 节点i的度为4, 集群系数为0.5.
无权网络能给出节点之间的相互作用存在与否的定性描述, 即提供任意节点是否连边的信息.而在实际网络中, 仅用边的连接与否并不能准确反映实际网络的全部功能, 对节点之间的相互作用强度的定量分析往往发挥着至关重要的作用.此时, 就需要引入边权来刻画节点间相互作用强度的差异性(李梦辉, 2008).例如, 因特网的带宽大小是衡量网络特征的重要指标.
因此, 在无权网络集群系数的基础上, 进一步提出了考虑边权的加权网络集群系数, 本文选用了Holme等(2007)所提出的加权网络的集群系数:
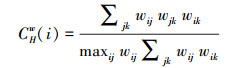
|
(5) |
式中, wij表示两个节点(i, j)所连边的边权, 若权值wij=0, 则表示节点i与j不存在连边;maxijwij是网络中的最大权重. 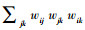
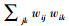
当然, Holme所提出的加权网络的集群系数仍存在一定的局限性, 这种局限表现在忽视了度对集群系数的影响.由于单纯的集群系数仅考虑了包含该节点的网络结构的完美度, 当节点的度较小时更容易出现较大的集群系数.以退化为无权网络的八节点网络图为例(图 3), 在整个网络体系中, 节点i的重要性大于节点o的重要性.但计算退化的加权集群系数发现, 节点o的度为3, 集群系数为0.33, 而节点i的度为5, 集群系数仅为0.3, 小于节点o的集群系数.显然, 仅考虑网络结构的集群系数并不能完全体现节点的重要性.因此本文将度的影响纳入集群系数中, 构造了一个度的权重w′i=ki/k, w′i是节点i的集群系数的权重, ki是节点i的度, k是所有节点的平均度.新的加权集群系数可以表示为:
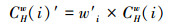
|
(6) |
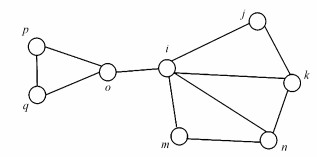 |
| 图 3 八节点网络图 Fig. 3 Network diagram of 8 nodes |
式中, 权重w′i可以理解为一个修正因子, 若节点i的度高于平均度, 即w′i>1, 则新的加权集群系数比原来的加权集群系数大;反之, 若节点i的度低于平均度, 即w′i<1, 则新的加权集群系数比原来的加权集群系数小.这样的修正会降低由于度的大小所带来的集群系数出现偏差的问题.同样以图 3为例, 计算节点i与节点o修正后的加权集群系数CHw(i)′与CHw(o)′分别为0.5和0.33, 表示节点i较节点o更为重要, 这与事实相符.
在修正的节点加权集群系数的基础上, 整个网络的集群系数可以表示为网络中所有节点集群系数的算术平均值, 记为:
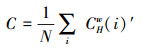
|
(7) |
网络的集群系数能有效反映整个网络的聚集程度, 若网络中某个节点的集群系数大于整个网络的集群系数, 则表示在整个网络中这个节点能对其他相邻节点带来较大的直接影响, 即处于相对重要的地位.因此集群系数在一定程度上能体现节点的重要性.
2.2 网络效率与脆弱性对于无权网络, 测地线定义为两个节点(i, j)之间边数最少的一条道路, 而测地线的边数就称为i, j之间的距离dij.如果考虑边权, 测地线的长应该定义为两个节点(i, j)之间各边权倒数之和的倒数(何大韧, 2009), 即:
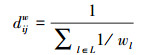
|
(8) |
式中, l表示“道路” L上的一条边, wl表示这条边的边权.
由于城市与城市之间的连接方式众多且经过两个或两个以上城市相连的权重几乎不足以影响两地的测地线长, 因此本文仅考虑节点i与节点j直接相连的“道路” lij , 即测地线长等于权重, 表示为:
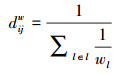
|
(9) |
网络效率是用来衡量网络连通性的好坏, 网络的连通性越好, 则网络效率越高.网络效率定义为(Jovica et al., 2017):
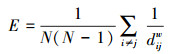
|
(10) |
基于网络效率可以进一步求出网络的脆弱性, 一个节点i的脆弱性定义为:
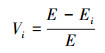
|
(11) |
式中, Ei表示从网络中去掉节点i之后的网络效率, E为未去节点的网络效率.由此可知, 若Ei<E, 则说明去掉节点i之后整个网络效率降低, 网络的脆弱性增加, 因此这类型节点属于网络中十分重要的节点;反之, 若Ei≥E, 则说明去掉节点i之后整个网络效率提高, 网络的脆弱性降低, 所以这一类型节点对于整个网络来说并没有起到明显作用.因此根据去除节点后的网络效率和脆弱性也可以分析节点的重要性.
2.3 基于度和集群系数的节点重要性综合评价方法度可以反映自身的连边状况却不能反映邻点的连边状况;相反, 集群系数可以反映邻点的连边状况却不能体现邻点的规模大小.若能将度和集群系数结合起来评价节点的重要性, 则会更科学也更全面.
在此基础上, 任卓明等(2013)综合考虑了节点的邻点个数及邻点间的连边情况, 提出了一种基于度和集群系数的节点重要性评价方法, 评价指标Pi可表示为:
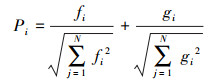
|
(12) |
式中, fi表示节点i的度与其邻点的度之和, 即fi= 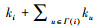
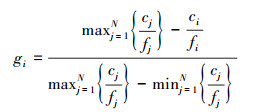
|
(13) |
式中, ci为节点i的集群系数.
对于式(12), fi反映的是自身的度与邻点的度的信息, 是反映节点规模的一种信息, 而gi反映的则是节点的邻点间的紧密程度, 是反映节点的邻点连通性的一种信息.最后使用同趋化函数对fi和gi处理得到了综合评价指标Pi, Pi越高则说明节点重要性越强.
3 实证研究(Empirical researches)雾霾污染物随着外部因素作用后的跨界传输使得京津冀地区形成了一个区域性的雾霾污染.然而由于地形、风向等影响, 城市与城市之间雾霾污染的相互联系、相互作用的程度并非一致, 从整个京津冀地区中找出真正的“重灾区”才能采取更有针对性的措施治理和防护雾霾污染.因此, 本文希望从整个京津冀区域的雾霾污染大网络中寻找到内部联系最为紧密、相关性最强的一个子网络.而节点的重要性评价将对子网络的选择发挥至关重要的作用.接下来本文将运用3种节点重要性评价方法进行实证分析.
由于京津冀地区最主要的雾霾污染物是PM2.5, 为了便于研究, 本文仅采用PM2.5这项指标反映雾霾污染的严重程度.为了构建京津冀地区雾霾污染网络, 本文以京津冀地区:北京、天津、石家庄、保定、廊坊、唐山、邢台、衡水、邯郸、承德、张家口、秦皇岛、沧州共13个城市作为研究对象, 选取2013年10月28日至2017年10月17日, 共1488 d内13个城市的日均PM2.5浓度数据作为样本, 单位为μg·m-3.
3.1 度与集群系数将京津冀13个城市作为节点, 以城市与城市间PM2.5日均浓度的Pearson相关系数作为是否连边的判别标准, 本文选取相关系数矩阵除对角线以外所有元素的均值为阈值, 这样的阈值选取方式会使得网络的拓扑性质稳定, 即最大连通子图节点个数的变化较为平稳(吴翎燕, 2013).本文通过这种方法计算求得的阈值为0.69.若相关系数大于阈值0.69则连接两个城市, 否则不建立连接关系.
然而由于雾霾污染物的传输也受城市间的距离、地势、气象条件、工业污染排放等诸多因素影响, 仅考虑相关系数作为边权并不能完全体现网络的空间关系.为了既体现这种网络节点的空间关系, 又不会造成过度拟合, 本文将城市间日均PM2.5浓度的相关系数与城市间最短距离的比值作为网络结构中边的权重(薛安, 2015), 由此构造出京津冀地区雾霾污染的加权网络.而在实际计算中, 为了消除城市间距离的量纲, 本文选取线性比例变换法, 即用距离除以最大距离得到一个范围在(0, 1]间的距离系数, 用相关系数除以距离系数得到边的权重, 同样再对边权进行线性比例变换法得到(0, 1]间的权重, 表 1为求得的权重邻接矩阵.
| 表 1 京津冀13市权重邻接矩阵 Table 1 Weighted adjacency matrix of 13 cities in Beijing-Tianjin-Hebei region |
由表 1可以发现, 以京津冀13个城市为节点, 每个节点的度分别是9(北京)、9(天津)、9(石家庄)、10(保定)、10(廊坊)、10(唐山)、8(邢台)、9(衡水)、4(邯郸)、3(承德)、0(张家口)、5(秦皇岛)、8(沧州).由于张家口节点是一个度为0的孤立点, 即不与网络中其他任意节点连边, 因此接下来的研究将去除张家口这个节点, 只考虑整个京津冀雾霾污染网络中其他的12个节点.
我们做出了京津冀雾霾污染网络中每个节点的连边情况及其形成的“三角形”和“三元组”的示意图(图 4).图 4由12个子图构成, 每个子图代表以相应城市为主节点所构成的“三角形”和“三元组”存在情况, 其中“三角形”两条邻边用实线绘制, 对边用虚线绘制, “三元组”两条邻边用实线绘制.从图 4可以大致看出12个节点的度的大小不一致, 邻点连边状况也互不相同, 但不难看出图 4(j)的主节点为承德, 承德度为3, 而3个邻点均两两相连, 即存在3个“三角形”和3个“三元组”, 这意味着若还是按照无权网络的集群系数进行计算, 承德节点的集群系数将为1, 显然这并不能有效反映承德节点重要性的真实水平.此时, 需要考虑加权网络的集群系数.
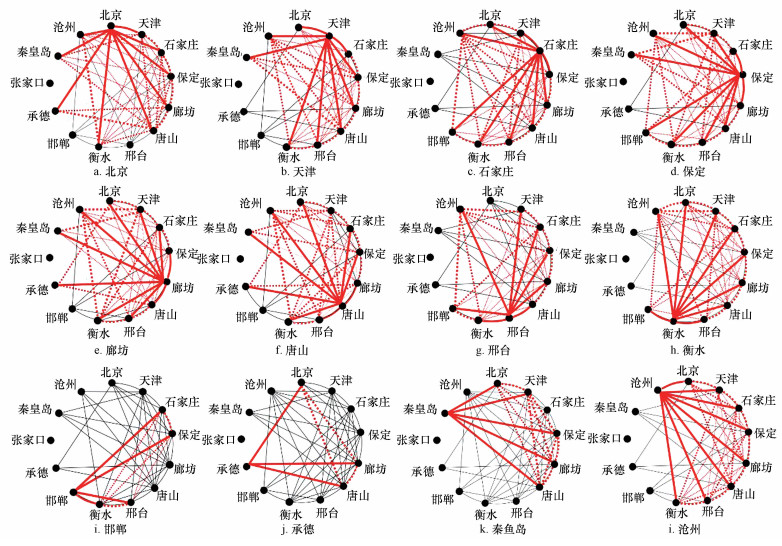 |
| 图 4 以12个城市为节点所构造网络中的“三角形”与“三环组” (注:实线代表节点的连边, 虚线代表两边构成三角形) Fig. 4 'Triangle' and 'three tuple' in the network constructed by 12 city nodes |
根据Holme所提出的加权网络每个节点的集群系数计算公式(式(5)), 求出了12个节点的集群系数, 结果见表 2.
| 表 2 以12个城市为节点的集群系数 Table 2 Clustering coefficient of 12 city nodes |
虽然在表 2中, 邯郸、承德、秦皇岛、的集群系数最高, 这表明3个城市的小集团结构的完美程度高, 但考虑到3个城市的度分别只有4、3、5, 在所有城市节点的度中分列倒数3位, 此时仅考虑集群系数没有任何现实意义.因此本文将度除以平均度作为权重, 利用式(6)求得加权集群系数(表 3)来反映真实的网络结构.
| 表 3 以12个城市为节点的加权集群系数 Table 3 Weighted clustering coefficient of 12 city nodes |
分析表 3中加上度权重的集群系数可以发现, 加权集群系数由高到低的城市节点分别是保定、唐山、石家庄、天津、廊坊、北京、沧州、衡水、秦皇岛、邢台、邯郸、承德.而这一结果也符合12个城市的地理位置特征, 排名前八的城市位于京津冀区域中部, 而排名末尾的四位中秦皇岛和承德位于京津冀区域的北部, 邢台与邯郸位于京津冀区域的南部.
进一步, 求出12个城市节点所构成网络的加权集群系数为0.2875.以网络的加权集群系数为标准, 若节点集群系数大于整个网络的集群系数, 则表示该节点十分重要;反之, 则表示该节点不太重要.依据这一规则可知, 保定、唐山、石家庄、天津、廊坊、北京、沧州、衡水这8个城市节点重要性较高, 而秦皇岛、邢台、邯郸、承德这4个城市节点重要性较低.以上结果表明, 以保定、唐山、石家庄、天津、廊坊、北京、沧州、衡水这8个节点为主节点, 节点的聚集程度高于平均水平, 意味着由节点及其邻点所生成的子网络内部连接更加紧密, 说明这8个城市节点能对其他城市节点带来更直接的影响, 即在整个京津冀雾霾网络中这8个城市相较于其他4个城市在雾霾污染上有更高的传输贡献.
3.2 网络效率与脆弱性首先通过式(10)求出整个网络的效率为3.3560, 接着对12个城市逐一进行去除, 并计算出去除一个节点后对应的网络效率和网络脆弱性(见表 4).
| 表 4 去除一个节点的网络效率及脆弱性 Table 4 Network efficiency and vulnerability after removing a node |
根据表 4中去除该城市节点后的网络效率由低到高排序分别是:唐山、保定、石家庄、廊坊、天津、北京、沧州、衡水、邢台、秦皇岛、邯郸、承德.通过网络脆弱性的定义(式(11))可知, 网络效率与网络脆弱性成负相关.因此, 网络脆弱性由高到低排序亦是如此.在表 4中, 分别去除了唐山、保定、石家庄、廊坊、天津、北京这6个城市节点后的网络效率均小于原来整个网络的效率, 同时脆弱性均大于0, 这说明去除这部分节点会使得整个网络的连通性变得差, 换言之会对整个网络的互通互联造成显著的破坏.而另一方面, 分别去除了沧州、衡水、邢台、秦皇岛、邯郸、承德这6个城市节点后的网络效率均大于原来整个网络的效率, 同时脆弱性均小于0, 这表明去除这些城市节点后对于整个网络的连通性不仅未起到太大的破坏, 反而还增加了整个网络的平均交通容易程度.其中沧州、衡水、邢台3节点相较初始网络效率增加并不显著, 分别只增加了0.0185、0.0274和0.0459个单位的效率值, 而秦皇岛、邯郸、承德3节点比初始网络效率分别增加0.2139、0.2342、0.3902个单位的效率值, 增加率分别为6.37%、6.98%、11.63%, 因此可以认为前者比后者在整个网络中占有更重要的地位.
3.3 节点重要性综合评价通过式(12)、(13)计算, 可以得到网络中各节点的属性(表 5).
| 表 5 网络中各节点属性 Table 5 Attribute of each node in the network |
表 5中最后一列为节点重要性评价指标Pi, 对Pi从大到小进行排序可以得到节点重要性排名:保定、廊坊、唐山、天津、石家庄、北京、衡水、邢台、沧州、秦皇岛、邯郸、承德.从Pi的值可以明显看出前9个城市节点的Pi均大于0.6, 且最大值和最小值相差仅有0.0604, 这说明前9个城市在整个网络体系中均属于重要节点.而秦皇岛、邯郸和承德3个城市节点的Pi分别仅为:0.3838、0.2113和0.1195明显小于其他9个节点, 所以我们可以将这3个节点列为重要性不高的节点.通过对表 5进行分析, 造成秦皇岛、邯郸和承德3个节点远低于其他9个节点的主要原因可能是3个节点的度远小于其他节点.进一步, 结合评价指标Pi的定义(式(12))分析可知, Pi的值非常依赖节点i的度与其邻点的度之和fi的值的大小, 即对于节点度的大小变化非常敏感, 较小的度将直接使得Pi也很小, 这也验证了上述猜想.
4 结论与建议(Conclusions and suggestions) 4.1 结论1) 通过度与集群系数所构造的节点加权集群系数, 秦皇岛、邯郸、承德、邢台这4个城市节点的加群集群系数均低于网络的集群系数0.2875, 属于重要性较低的4个节点;而排名前6的城市节点为保定、唐山、石家庄、天津、廊坊、北京, 它们的加群集群系数均高于0.3220, 显著高于其他节点, 因此属于重要性较高的6个节点;剩下的沧州、衡水两个节点的加群集群系数略高于网络的集群系数, 属于较为重要的节点.
2) 运用网络效率与脆弱性对节点重要性进行评价可知, 去除秦皇岛、邯郸、承德3节点后的网络效率比初始网络效率有显著的增加(增加率分别为:6.37%、6.98%、11.63%), 因此这3个节点对于整个网络的重要性不高.而去除唐山、保定、石家庄、廊坊、天津、北京这6个节点会使得整个网络的效率降低、脆弱性增强, 这表明这6个城市节点对于整个网络的通行效率有着决定性的作用, 在网络中处于重要的地位.
3) 采用基于度和集群系数的节点重要性综合评价方法, 保定、廊坊、唐山、天津、石家庄、北京、衡水、邢台、沧州这9个城市节点的节点重要性评价指标Pi均大于0.6, 且排名第9的沧州与排名第1的保定评价指标Pi仅相差0.0604, 因此可以认为这9个节点都属于重要的节点.而秦皇岛、邯郸和承德3个城市节点的Pi分别仅为:0.3838、0.2113和0.1195明显小于其他9个节点, 因此属于重要性排名靠后的3个节点.
通过分析3种方法得到的结果可以发现:保定、廊坊、唐山、天津、石家庄、北京在三种方法的结果中均位列前6, 因此是整个京津冀雾霾污染网络中的核心节点.而秦皇岛、邯郸、承德3个节点均排名倒数, 因此可以认为秦皇岛、邯郸、承德节点重要性低, 在整个京津冀雾霾污染网络中是可以去除的节点.而沧州、衡水、邢台3个节点属于较为重要的节点.综合上述分析, 本文给出了一个相对科学的节点重要性排名, 按照重要性由高到低分别是保定、唐山、廊坊、石家庄、天津、北京、沧州、衡水、邢台、秦皇岛、邯郸、承德.
基于上述节点重要性评价综合结果, 本文在原有的京津冀雾霾污染大网络的基础上提取出了联系最为紧密、相关性最强的一个雾霾污染子网络, 子网络一共包含9个城市节点, 分别是保定、唐山、廊坊、石家庄、天津、北京、沧州、衡水、邢台(图 5).
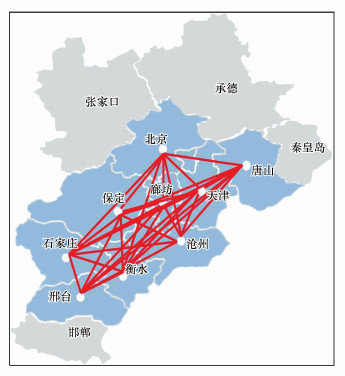 |
| 图 5 京津冀地区雾霾污染子网络示意图 Fig. 5 Diagram of haze pollution subnetwork in Beijing-Tianjin-Hebei region |
分析图 5的地理位置信息不难发现, 邯郸位于京津冀地区最南端, 秦皇岛、承德、加之构建网络时去除在外的孤立节点张家口均位于京津冀地区最北端, 这四个城市都属于京津冀的“边缘城市”, 它们受制于距离、污染物排放、气象条件及地势等诸多因素的影响, 对区域内其他城市带来雾霾污染方面的影响相对较低, 因此被排除在真正的“重灾区”—京津冀雾霾污染子网络之外.而其他9个城市则形成了一个相互联系紧密且节点较为集中的子网络, 其中保定、廊坊、唐山、石家庄、天津、北京这6个最重要的城市节点均位于整个京津冀地区的中部, 6个城市连接起来形成一个狭长的带状区域, 对区域内其他城市节点影响极大, 属于京津冀雾霾污染网络中需要重点加强防控的城市.
4.2 政策建议在京津冀雾霾污染子网络中城市节点之间发生雾霾天气存在着显著的相关性, 而这种节点间的显著相关性会使得雾霾污染呈现出区域性特征.为了有效降低这种区域性雾霾污染的影响, 我们认为, 应当推进京津冀雾霾污染子网络内雾霾污染防治一体化, 实现区域内雾霾污染联合治理、协同治理.为了更好地促进形成京津冀地区雾霾污染防治一体化格局, 提出如下建议:
首先, 以京津冀雾霾污染子网络中的9个节点城市(保定、廊坊、唐山、石家庄、天津、北京、沧州、衡水、邢台)为主, 设立区域联合监督管理部门, 根据该区域特点统筹规划, 制定一套切实可行的联控联防机制, 有效协调各地区各部门间的沟通.特别是针对节点重要性排名前6的城市:保定、廊坊、唐山、石家庄、天津、北京, 要加大监控力度, 通过严格监管这6个主要城市使得整个雾霾污染网络连通效率降低, 进而达到降低整个区域雾霾污染的效果.
其次, 进一步完善大气污染防治的政策法规.制订符合实际的政策法规, 突破传统行政体系的约束, 实现跨地区跨部门的协同合作, 共同应对雾霾污染问题带来的影响.
最后, 在区域内建立起完善、统一、高效的大数据信息平台.雾霾污染网络内各个地区, 将每一时刻每个空气质量监测点所监测到的相关污染物浓度、风向、等相关数据实时上传至平台, 并通过大数据信息平台对收集到的所有结构化与非结构化数据进行处理及分析, 再将分析得到的结果即时反馈给各地区相关部门, 从而采取有针对性的措施对空气污染问题进行治理.
Barabási A L, Albert R. 1999. Emergence of scaling in random networks[J]. Science, 286(5439): 509–512.
DOI:10.1126/science.286.5439.509
|
段玉森, 魏海萍, 付晴艳, 等. 2008. 中国环保重点城市API指数的时空模态区域分异[J]. 环境科学学报, 2008, 28(2): 384–391.
|
方锦清, 汪小帆, 郑志刚, 等. 2007. 一门崭新的交叉科学:网络科学(上)[J]. 物理学进展, 2007, 27(3): 239–343.
|
Gao M, Carmichael G R, Wang Y, et al. 2016. Modeling study of the 2010 regional haze event in the North China Plain[J]. Atmopheric Chemistry and Physics, 16(3): 1673–1691.
DOI:10.5194/acp-16-1673-2016
|
郭世泽, 陆哲明. 2012. 复杂网络基础理论[M]. 北京: 科学出版社: 170–179.
|
何大韧, 刘宗华, 汪秉宏. 2009. 复杂系统与复杂网络[M]. 北京: 高等教育出版社: 117–119.
|
Holme P, Park S M, Kim B J, et al. 2007. Korean university life in a network perspective: Dynamics of a large affiliation network[J]. Physica A: Statistical and Theoretical Physics, 373: 821–830.
DOI:10.1016/j.physa.2006.04.066
|
黄晓波, 殷晓鸿, 黄志炯, 等. 2016. 不同模式对珠三角地区细颗粒物污染模拟效果对比评估[J]. 环境科学学报, 2016, 36(10): 3505–3514.
|
Jin Q, Fang X, Wen B, et al. 2017. Spatio-temporal variations of PM2.5 emission in China from 2005 to 2014[J]. Chemosphere, 183: 429–436.
DOI:10.1016/j.chemosphere.2017.05.133
|
Li J, Du H Y, Wang Z F, et al. 2017. Rapid formation of a severe regional winter haze episode over a megacity cluster on the North China Plain[J]. Environmental Pollution, 223: 606–615.
|
李梦辉, 樊瑛, 狄增如. 2008. 加权网络的结构、功能和演化[A]. 第三届全国复杂网络学术会议文集[C]. 香港: 上海系统科学出版社. 107-143
|
刘华军, 孙亚男, 陈明华. 2017. 雾霾污染的城市间动态关联及其成因研究[J]. 中国人口·资源与环境, 2017, 27(3): 74–81.
|
刘建国, 任卓明, 郭强, 等. 2013. 复杂网络中节点重要性排序的研究进展[J]. 物理学报, 2013, 62(17): 178901.
DOI:10.7498/aps.62.178901 |
Milanovic J V, Zhu W T. 2017. Modelling of interconnected critical infrastructure system using complex network theory[J]. IEEE Transactions on Smart Grid: 1–12.
|
任卓明, 邵凤, 刘建国, 等. 2013. 基于度与集群系数的网络节点重要性度量方法研究[J]. 物理学报, 2013, 62(12): 128901.
DOI:10.7498/aps.62.128901 |
Tobler W. 1970. A computer movie simulating urban growth in the detroit region[J]. Economic Geography, 46(2): 234–240.
|
王斌. 2008. 利用空气污染指数(API)分析我国空气污染的区域时空变化特征[D]. 青岛: 中国海洋大学. 22-31
http://cdmd.cnki.com.cn/Article/CDMD-10423-2008176194.htm |
Watts D J, Strogatz S H. 1998. Collective dynamics of Small-World networks[J]. Nature, 393(6638): 440–442.
|
吴翎燕, 韩华, 宋宁宁. 2013. 基于相关系数和最佳阈值的股票网络模型构建[J]. 复杂系统与复杂性科学, 2013, 10(4): 49–55.
|
薛安, 耿恩泽. 2015. 基于复杂网络的中国城市PM2.5区域划分[J]. 应用基础与工程科学学报, 2015, 23: 68–78.
|
薛文博, 付飞, 王金南, 等. 2014. 中国PM2.5跨区域传输特征数值模拟研究[J]. 中国环境科学, 2014, 34(6): 1361–1368.
|
杨博, 刘大有, LiuJ, 等. 2009. 复杂网络聚类方法[J]. 软件学报, 2009, 20(1): 54–66.
|
张晓勇, 王仲军. 2014. 城市PM2.5扩散网络模型的研究[J]. 中国环境监测, 2014, 30(6): 129–132.
|
张志刚, 高庆先, 韩雪琴, 等. 2004. 中国华北区域城市间污染物输送研究[J]. 环境科学研究, 2004, 17(1): 14–20.
|
 2018, Vol. 38
2018, Vol. 38


