随着人口的增长和社会经济的高速发展，20世纪80年代以来，生态安全逐渐成为环境研究的重要组成部分，目前已成为环境科学、生态研究的前沿和热点课题(Westing，1989；陈星等，2005；Wei et al.,2009；秦晓楠等，2014).作为人口高度集聚的生态系统，城市生态系统的安全性更加脆弱，环境污染、资源稀缺等引发的生态安全问题威胁和制约了城市经济社会的可持续发展.城市生态安全问题逐渐受到广泛关注，并成为生态安全研究的主要方向之一，其研究主要集中在生态安全评价方面(Gong et al.,2009；Pei et al.,2010；Xiao，2011；Shao et al.,2013).目前具有代表性的评价方法有模糊综合法(李佩武等，2009)、物元分析法(张松男等，2013)、主成分分析法(陈菁等，2010)、灰色关联法(吴晓等，2014)等，这些模型在生态安全评价中得到了较好的应用，但仍存在一些共性问题，即忽略了生态安全体系内各要素的关联性和耦合性，导致模型结果不能有效揭示生态安全的作用机理和动态演化，难以对生态安全的发展趋势进行预测.根据城市生态安全的内涵，以复杂系统观点审视城市生态系统，用信息熵刻画系统结构，构建相应的评价指标体系及评价模型，多层次、多角度、全方位地评判城市生态安全状况，对于改善城市生态环境质量、维持城市可持续发展具有重大的理论与现实意义.

宁波位于浙江宁绍平原东端，长江三角洲南翼，是浙江省副省级城市.该市包括6个区、3个县级市和2个县，全市总面积9365 km²，属于典型亚热带季风气候.作为长江三角洲南翼经济中心和浙江省三大经济中心之一，宁波的社会经济发展显示出巨大的活力和潜力，将在今后相当长的时间内呈持续快速发展状态，同时，宁波的生态系统也将面临巨大的压力.因此，科学评价宁波市的生态安全状况，了解城市发展过程面临的生态环境问题，可为管理者提供科学的依据与指导，对于实现宁波市的可持续发展具有重要意义.因此，本文在研究城市生态安全概念理论的基础上，建立宁波市生态安全评价指标体系，并引入信息熵的概念，依据最大信息熵原理(MIEP)推出城市生态系统演化的动力学方程，建立城市生态安全评价的数学模型，揭示宁波市生态安全系统的动态演化并展开评价和相关研究.

城市生态安全是城市生态系统在保持其结构和功能不受威胁或少受威胁的健康、平衡状态的前提下，能够为人类生存和城市可持续发展提供稳定、均衡的各种资源，从而维持自然、社会、经济复合体的长期协调发展(陶晓燕等，2010).生态安全首先是自然子系统为人类活动提供的承载、缓冲、支持、供给能力的安全，主要体现在人与水、土、能、生物、地球化学循环等5类因子相互耦合形成的生态过程的安全，其次是经济子系统为人类提供的生产、消费和调控功能等的安全，最后是涉及个体和群体心理、生理等健康的人口生态安全(王如松，2007).改善经济发展与自然环境之间的矛盾，是提高城市生态安全程度的主要途径，也是实现低碳城市和生态城市建设的必备条件，并最终实现工业文明向生态文明的转化.

城市生态安全评价就是根据经济社会持续发展与生态安全影响因子间的关系，在分析生态环境对社会经济持续发展的影响与制约的基础上划定生态安全与不安全的界线，对生态安全程度予以区分的方法(周国富，2003).

目前国内外建立和应用的城市生态安全评价指标体系主要有PSR(压力-状态-响应)模型(殷春雪等，2013；Bai et al.,2010)、DSR(驱动力-状态-响应)模型(谈迎新等，2012)、DPSIR(驱动力-压力-状态-影响-响应)模型(刘世栋等，2012)、DPSER(驱动力-压力-状态-暴露-响应)模型(Zuo et al.,2005)等.其中，最为常见的是PSR模型，该模型强调经济运作与环境之间的联系，逻辑关系清晰，可操作性强.在PSR模型下，压力指标是引起生态安全问题的原因，选取经济压力、土地压力、资源压力和环境压力4个要素；状态指标用来衡量人为造成的自然环境状况的质量，选取资源质量和环境质量2个方面；响应指标是表征人类社会应对生态安全危机的能力，用污染控制响应、经济投入响应和人文社会响应3个要素反映.结合城市生态安全的内涵，依据科学性、系统性、可操作性、实用性等指标选取的原则，参考相关文献(陶晓燕等，2010；龚建周等，2006；李莹，2013)，分别从自然、经济、社会子系统方面选取了各要素层的评价指标，构建了宁波市生态安全评价指标体系，具体如表 1所示.表 1中各评价指标的原始数据可通过查阅宁波统计年鉴、中国环境年鉴、中国城市统计年鉴、统计公报等资料获得.

表 1(Table 1)

表 1 宁波市生态安全评价指标体系及指标分级标准 Table 1 Assessment indicator system and grading st and ards of indicators

表 1 宁波市生态安全评价指标体系及指标分级标准 Table 1 Assessment indicator system and grading st and ards of indicators 要素层 指标层 单位 分级标准 不安全 较不安全 临界安全 较安全 安全 经济压力 x1城市居民恩格尔系数 ＞45% 45%~40% 40%~35% 35%~30% ＜30% x2人均GDP 万元 ＜1 1~3 3~5 5~12 ＞12 土地压力 x3人均住房建筑面积 m2 ＜20 20~25 25~30 30~37 ＞37 x4人均城市道路面积 m2 ＜6 6~10 10~15 15~20 ＞20 x5人均公园绿地面积 m2 ＜4 4~9 9~13 13~18 ＞18 资源压力 x6单位GDP能耗 t标煤·万元-1 ＞2 2~1.5 1.5~1 1~0.5 ＜0.5 x7单位GDP用水量 m3·万元-1 ＞225 225~175 175~75 75~20 ＜20 环境压力 x8 COD排放强度 kg·万元-1 ＞6 6~4.5 4.5~2.5 2.5~1.3 ＜1.3 x9工业废气排放强度 m3·万元-1 ＞10000 10000~8000 8000~5000 5000~3500 ＜3500 资源质量状态 x10建成区绿化覆盖率 ＜20% 20%~25% 25%~35% 35%~45% ＞45% x11饮用水源水质达标率 ＜85% 85%~92.5% 92.5%~97.5% 97.5%~100% 100% 环境质量状态 x12地表水功能区达标率 ＜30% 30%~50% 50%~70% 70%~90% ＞90% x13空气质量优良率 ＜70% 70%~80% 80%~85% 85%~90% ＞90% x14降水pH年均值 ＜4.0% 4.0%~4.5% 4.5%~5.0% 5.0%~5.6% 5.6% x15噪声达标区覆盖率 ＜30% 30%~50% 50%~75% 75%~95% ＞95% 污染控制响应 x16工业废水排放达标率 ＜70% 70%~80% 80%~90% 90%~100% 100% x17工业用水重复利用率 ＜30% 30%~50% 50%~70% 70%~85% ＞85% x18城镇生活污水处理率 ＜20% 20%~40% 40%~60% 60%~80% ＞80% x19工业SO2去除率 ＜50% 50%~60% 60%~80% 80%~100% 100% x20 COD去除率 ＜70% 70%~80% 80%~90% 90%~100% 100% x21工业固体废物综合利用率 ＜60% 60%~80% 80%~90% 90%~95% ＞95% x22城市生活垃圾无害化处理率 ＜75% 75%~85% 85%~95% 95%~100% 100% 经济投入响应 x23环保投资指数 ＜1.5% 1.5%~2% 2%~2.5% 2.5%~3% ＞3% x24第三产业占GDP比重 ＜20% 20%~40% 40%~60% 60%~70% ＞70% x25 R&D经费占GDP比例 ＜1% 1%~1.25% 1.25%~2.0% 2.0%~3.1% ＞3.1% 人文社会响应 x26万人拥有病床数 张 ＜20 20~40 40~70 70~90 ＞90 x27万人在校大学生数 人 ＜150 150~350 350~700 700~1000 ＞1000

基于广义信息熵，柴立和等认为城市是一个由广义信息生成的有机复杂整体，其内在的及其与外界的物质、能量流动构成了一幅动态的信息流动图像(Chai et al.,2004).这种“流”载于结点之间的连接上，也可理解为具有相互作用功能的某种联系，对特定系统性质起决定作用.作为一个典型的复杂系统，城市生态系统的演化规则遵循MIEP，即给定约束或代价下使广义信息熵最大的分布是最没有偏差的、最可能出现的分布，一个远离平衡态的复杂开放系统总是寻找一种优化过程使得系统在给定的约束或代价下从外界获得的广义信息熵最大(Jaynes，1957；Chai et al.,2002).从信息熵角度看，城市生态安全评价就是根据城市经济社会持续发展与生态安全影响因子间的信息流分配划分安全程度.结合城市生态安全的内涵，可构建一个以宁波市生态安全评价指标为结点(x_i)的信息网络结构，具体见图 1，指标之间的相互作用通过“流”来实现，此时x_i称为信息结构的组元.城市生态安全评价因素间无穷的联系及耦合的关系用信息熵S_J表示为：

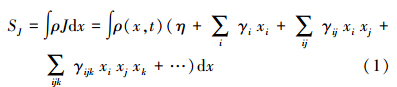
式中，ρ(x，t)为测度，η为常数，各类γ是反映组元相互作用的系数，J为不均匀联系的分布函数，类似笛卡尔乘积.

图 1(Fig. 1)

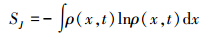
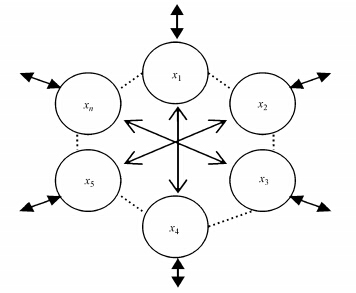图 1 宁波市生态安全的信息网络结构示意图 Fig. 1 Information network structure diagram of ecological security in Ningbo

城市生态系统演化的动力学过程必然受到一些因素的约束，这种约束条件可以转化成组元或结点之间应满足的守恒关系，即质量连续性方程、动量守恒方程、能量守恒方程等，可一般化的用x₁，x₂，…，x_n表示为:

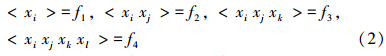
式中，<>表示求统计平均值，如<x_i>=f₁即为.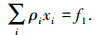

根据MIEP，宁波城市生态系统寻求安全状态的过程是在约束条件(2)下信息熵S_J最大化的过程.利用Lagrange乘算法使式(1)在式(2)下取极值，由泰勒展开式得：

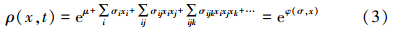
式中，势函数φ控制着系统组元相互作用而形成有序结构的动力学过程，参数μ、σ等反映组元相互作用的微观动力学规则，其值取决于难以获得的f₁~f₄.将φ进行平移变换，对变换后的二阶常数项矩阵对角化，引入变量ξ_k=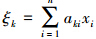 a_kix_i，则φ变为：

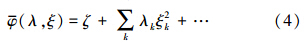
式中，ξ_k是x_i的组合模式，代表城市生态安全的结构模式；a_ki是系统与x_i之间的连接权值，表示x_i对城市生态安全的贡献能力；λ_k是矩阵a_ki的特征值，最大λ_k对应的系统的组合模式ξ_k是评价系统状态的关键参量，ζ是常数.

依据式(5)，可推出动力学演化方程(6).

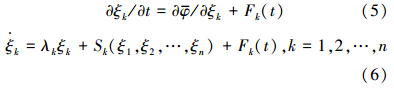
式中，F_k为随机力函数，S_k是非线性作用函数.城市生态系统内部组元的竞争、协同等相互作用调节了系统的运行状态和趋势，即组元之间通过不同的合作和竞争方式形成不同的功能结构模式ξ_k，并最终产生竞争获胜模式ξ，即在约束或代价下获得广义信息熵最大，能够最终涌现的稳定模式，它代表了该阶段宁波市的生态安全状况.式(6)反映了由变化的组元x₁，x₂，…，x_n驱动的动力学演化过程，可作为判断和分析城市生态安全各种状态模式(即广义流分配的模式)稳定性的基础.由此，基于MIEP的宁波市生态安全评价模型建立.

自组织特征映射神经网络(SOFM)是由大量简单的神经元广泛互连形成的复杂非线性系统，它能抓住输入数据的特征，自动组织其空间结构，并能无监督地进行自组织学习.其工作机理与上述模型的动力学过程相似，与MIEP控制下的复杂系统演化过程具有对应性.将宁波城市生态系统的组元x₁，x₂，…，x_n映射到SOFM网络的人工神经元上，通过模拟激发某个神经产生连接权值w_ij(对应模型中的a_ki)，同时获得ξ_k的波动过程，最终产生获胜结构模式ξ的值.这样，我们可以通过数学软件MATLAB编程，实现式(6)的求解，即得到表征城市生态安全状态的特征值ξ，实现对城市生态安全状况的量化.

根据数学模型的评价步骤，首先将评价指标数据无量纲化，然后依次代入上文建立的SOFM网络中进行分类分析，借助MATLAB计算平台，分别得到能够反映宁波市城市生态压力指标、状态指标和响应指标的特征值，具体见表 2.

表 2(Table 2)

表 2 宁波市2002—2011年各评价指标的特征值 Table 2 Evaluation index data of Ningbo during 2002—2011

表 2 宁波市2002—2011年各评价指标的特征值 Table 2 Evaluation index data of Ningbo during 2002—2011 年份 压力指数 状态指数 响应指数 2002 2.1759 4.0276 5.0617 2003 2.1862 4.0304 5.1134 2004 2.4865 3.9908 5.4489 2005 2.6896 4.4940 5.7658 2006 2.8269 3.9404 6.0537 2007 2.8219 3.8850 6.6237 2008 4.1116 3.8286 6.6737 2009 4.494 3.8735 6.4750 2010 5.9894 3.7890 6.6070 2011 6.1353 3.9233 6.7106

把表 2中的数据代入本文建立的SOFM网络中，计算宁波市2002—2011年表征城市生态安全的ξ值(ξ₁~ξ₁₀)，动态演化的模拟训练结果如图 2所示.图 2展示了在给出不同评价指标参数后，系统内部组元在约束条件下不断进行竞争、协调和自组织，最终产生反映其安全状况的获胜模式的过程，该获胜模式对应的ξ值表征了宁波市的城市生态安全状况.作为一个动态变化的复杂系统，城市生态安全指标每年都在变化，信息网络中组元之间的耦合关联不同，连接权值也在变化之中，所以2002—2011年的获胜模式不同.由图 2可知，模拟前期ξ值波动较大，后期趋于稳定，表明城市生态系统在相互作用中遵循MIEP逐渐达到了相对稳定的模式，可用稳定后的ξ值代表城市生态安全的综合状况.ξ值越大，城市生态系统的安全程度越高，城市的可持续发展性越强.

图 2(Fig. 2)

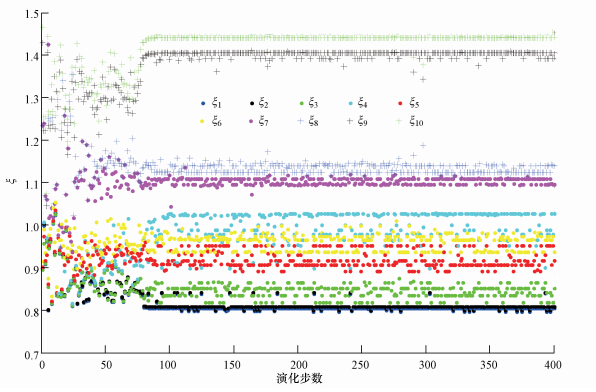图 2 宁波城市生态安全的动态演化图 Fig. 2 Dynamic evolution of Ningbo ecological security

宁波城市生态安全的ξ值在2002年为0.8090，之后逐年增大，2011年达到1.4808，表明宁波的城市生态安全状态逐年转好.与采用AHP法得到的评价结果相比(李莹，2013)，它们的走势情况基本一致(图 3)，验证了应用MIEP模型评价城市生态安全的可行性和合理性.

图 3(Fig. 3)

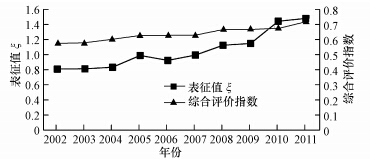图 3 宁波城市生态安全变化趋势 Fig. 3 Ecological security trends in Ningbo

城市生态安全评价标准是评价的关键环节，但目前还没有统一制定的评价标准，一般将城市生态安全划分为不安全、较不安全、临界安全、较安全和安全5个级别(张凤太等，2008).对于各评价指标，尽量以国内或国际标准为安全级别的最优值，没有规定值的参考生态市建设的指标建议值、国内外领先城市的现状值或宁波市的规划目标值等，以全国最低值或公认警戒线为不安全的限定值；在前者基础上向下浮动20%作为较安全和临界安全的标准值，在后者基础上向上浮动20%作为较不安全和临界安全的标准值，前后两次确定的临界标准值相互调整得到最终值，具体如表 1所示.根据评价指标分级标准及MIEP模型，得到的城市生态安全评价分级标准见表 3.

表 3(Table 3)

表 3 评价分级标准 Table 3 Evaluation classification st and ards

表 3 评价分级标准 Table 3 Evaluation classification st and ards 安全级别 不安全 较不安全 临界安全 较安全 安全 ξ值 ＜0.3330 0.3330~0.6065 0.6065~1.2460 1.2460~2.5272 ＞2.5272

将城市生态安全5个级别的最终主导模式的耦合关联量化时，需和宁波市生态安全评价在同一网络下进行，即设定相同的参数，进行相同的数据标准化处理，这是由SOFM网络的性质决定的.结合表 3中的分级标准，以及数值模拟过程中得到的ξ值，得到了宁波市各年份的城市生态安全级别，具体见表 4.

表 4(Table 4)

表 4 宁波市2002—2011年安全级别 Table 4 Security level from 2002 to 2011 in Ningbo

表 4 宁波市2002—2011年安全级别 Table 4 Security level from 2002 to 2011 in Ningbo 年份 ξ值 安全级别 2002 0.8090 临界安全 2003 0.8119 临界安全 2004 0.8324 临界安全 2005 0.9891 临界安全 2006 0.9238 临界安全 2007 0.9945 临界安全 2008 1.1242 临界安全 2009 1.1482 临界安全 2010 1.4434 较安全 2011 1.4808 较安全

宁波市2002—2009年城市生态安全处于临界安全状态，2010和2011年处于较安全状态，而且代表城市生态安全的ξ值，除2006年略有下降外，其余年份稳定增长，其生态安全水平稳步提高.这与宁波市的经济发展政策和规划是密不可分的.2002—2011年期间，宁波市逐渐加大科技和环保等方面的投入，以保护城市社会经济快速发展冲击下的生态环境，且取得了较好的成绩，城市生态安全水平逐渐提高.2004年，宁波市制定了《宁波生态市建设规划》，致力于建设成人与自然和谐相处的可持续发展城市，故2005年ξ值有较大幅度的上升，经不断发展和调整，2011年达到1.4808，但与理想的安全水平还有一定的差距.

由于评价系统是由信息关联耦合在一起形成的稳定结构模式，如式(6)描述那样是由它的结构参量ξ控制的，所以掌握组元与ξ之间作用关系的规律后，MIEP模型也可预测城市生态安全状态所对应结构模式的演化趋势，即根据某个组元数据来预测总体结构的ξ值.调控方法是在x_i-ξ关联图上作相应延展或插值，以此再现组元相互作用的动力学过程和结构模式的演化.根据广义流分配形式，在确定城市生态安全的主要影响因素后，可通过该组元与结构模式之间的关系对ξ值进行预测.

为了解2002—2011年期间各评价指标与城市生态安全的关系，找出与宁波市生态安全变化关联性较高的评价指标，将根据MIEP模型的输入与输出做相关性分析.通过x_i-ξ之间的拟合关系，得到了x_i与ξ值的相关系数R²(图 4).相关系数越高，说明x_i-ξ之间的拟合关系式越精确，利用此关系式进行预测得到的结果更符合实际.

图 4(Fig. 4)

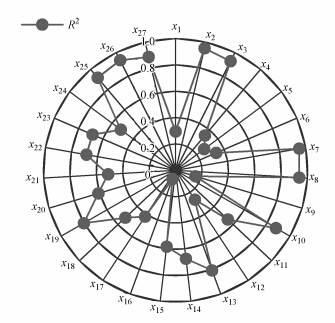图 4 各指标与城市生态安全指数的拟合关系 Fig. 4 Fitting relationship between indicators and urban ecological security index

结果表明，x₂、x₃、x₇、x₈、x₁₀、x₁₃、x₁₉、x₂₅、x₂₆和x₂₇等10个指标与城市生态安全综合指数的相关性较好，其中最好的是x₂和x₇，R²分别为0.9518和0.9501.由此可判断2002—2011年期间，人均GDP、人均住房建筑面积、单位GDP用水量、COD排放强度、R&D经费占GDP比例、万人拥有病床数等指标因素的变化趋势与宁波市生态安全的变化情况有密切关系.根据上述分析，利用这些指标进行宁波市生态安全的预测，得到的结果比较准确和可靠，下文将选取相关系数较高的人均GDP、单位GDP用水量、R&D经费占GDP比例、万人拥有病床数4项指标为例进行预测.将2012年的人均GDP无量纲化后代入拟合关系中求出ξ值为1.6460，进而根据ξ值求出其他3项指标的理论值，并将其与实际值相比(表 5)，用同样的方法求出2013年的各项理论值及误差.结果表明，2012年和2013年宁波的城市生态安全处于较安全级别，指标的实际值与理论预测值之间的误差均比较小，且相关系数越高，预测的误差越小，证实了MIEP模型用于城市生态安全预测的潜力.在实际工作中，可利用该模型根据相关性较高的某个指标在特定年份的设定期望值进行情景预测，以了解未来特定年份的城市生态安全状况，并得到为实现这一安全状况其他指标发展需达到的水平，为城市规划管理人员提供参考.

表 5(Table 5)

表 5 模型的预测值与实际值的对比 Table 5 Comparison of actual and predictive values from model

表 5 模型的预测值与实际值的对比 Table 5 Comparison of actual and predictive values from model 指标 拟合关系 R2 xi(实际值) xi(预测值) ξ 误差 2012年 2013年 2012年 2013年 2012年 2013年 2012年 2013年 x2 ξ=0.7019 x22+0.3463x2+0.6826 0.9518 114065 123139 114065 123139 1.6460 1.7771 0 0 x7 ξ=1.597 x72+0.7173x7+0.6326 0.9501 33.0 31.0 33.2 30.7 1.6460 1.7771 0.61% 0.97% x25 ξ=3.274x252-0.9422x25+0.8851 0.9179 2.04 2.21 2.01 2.12 1.6460 1.7771 1.47% 4.07% x26 ξ=19.967x262-11.854x26+2.5781 0.9351 49.00 49.60 45.04 46.40 1.6460 1.7771 8.08% 6.45%

本文从复杂系统组元相互作用动力学的角度建立了评价城市生态安全的MIEP模型，并用该模型对宁波市2002—2011年的城市生态安全进行了评价，建立了MIEP模型下的评价分级标准.结果表明，宁波市的生态安全状况逐年好转，2002—2009年处于临界安全状态，2010和2011年处于较安全状态，但离理想的安全水平还有很大差距.为保障宁波市未来相当长时间内的可持续发展，还需要继续努力.利用MIEP模型评价城市生态安全，在揭示系统在内部组元的相互作用下形成不同结构模式的动态过程的同时，能够自主获取各组元的连接权值，最终得到的“获胜模式”就代表城市生态安全的状态，且可用参量ξ的值定量评价，结果更客观.根据MIEP的工作机理，它在预测未知年份的生态安全程度上也有较大的潜力.