0 引言

地震定位是地震学研究的基础问题之一，如何提高地震定位精度是国内外研究者一直关注的重点。大量研究结果表明，速度模型是影响地震定位结果的关键因素。目前，大多数地震定位程序都采用一维速度模型，这是因为对台站数据结果进行处理后发现，在精度允许的情况下，一维速度模型具有成本较低、效率较高的优势，且更具普适性。此外，一维速度模型也是区域地震构造研究的重要基础。因此，建立较准确的一维速度模型对于提高地震定位精度和区域地震构造研究有着重要作用。

Kissling等(1994)提出了“最小一维速度模型的算法”，该算法可在进行地震定位的迭代过程中不断调整震源位置和速度模型，以使得地震定位结果的走时均方根残差和数据方差均达到最小，这样最终得到的速度模型被称为“最小一维速度模型”(高源等，2019)。目前，该算法被广泛应用于地震定位和初始速度模型的确定。

研究区位于西南天山地区柯坪块体。该块体是新疆乃至全国6级地震活动的主要区域，由于活动断裂发育，地震活动强度大，频度高，也是全国地震重点危险区划定次数最多的构造区域之一(南芳芳等，2018)。虽然在国内Velest算法已有广泛应用，但未见应用于柯坪块体的相关报道。因此，选取2018年6月至2020年5月柯坪块体及其周边数字地震台站记录的M_L≥2.0地震，尝试通过Velest算法反演柯坪块体最小一维P波速度模型，以期进一步提高柯坪块体地震定位精度，为新疆其他复杂地壳结构模型的研究提供参考。

1 区域构造及地震活动背景

新生代以来，印度板块与欧亚板块的碰撞及之后的向北推挤，形成了著名的青藏高原和中亚的活动山系(Molnar et al，1975，1978，1989；Tapponnier et al，1977，1979；Avouac et al，1993；张培震等，1996；杨晓平等，2008)。同时，新生代以来印度板块与欧亚板块的碰撞造成的远程效应导致了天山造山带的隆起，也推动了新疆“三山夹两盆”的构造地貌格局(Molnar et al，1975；Tapponnier et al，1979；Windley et al，1990；Allen et al，1993；邓起东等，2000；Thompson et al，2002；田勤俭等，2006)。“三山夹两盆”：山脉与盆地相间排列，盆地被高山环抱，北为阿尔泰山，南为昆仑山，天山横亘中部，把新疆分为南北两半，南部是塔里木盆地(内有塔里木河、塔克拉玛干沙漠)，北部是准噶尔盆地。天山两侧盆—山交会部位的近EW向逆冲褶皱系控制了天山主体发育，是现今变形最为强烈的部位(Molnar et al，1975；Avouac et al，1993；张培震等，1996；邓起东等，2000)，同时也是天山地震构造区重点研究部位。柯坪推覆体正是在这种构造格局下形成的最新活动构造，其特点是活动断裂发育，以NNW走向的皮羌断裂为界，可将柯坪推覆体分为东、西2部分。块体西侧发育4排逆断裂—褶皱带，东段发育5—6排逆断裂—褶皱带，这些背斜的主体由古生代地层组成，断层在背斜南翼出露地表，柯坪推覆构造的滑脱面发育在地下5—9 km的深度，地表的褶皱带是滑脱面向上翘起产生断坡而形成的背斜构造，向北缓倾的滑脱面在天山根部汇聚到迈丹断裂上。

从地震活动性上看，研究区属于中强地震频发区域，具有较强的中强地震活动背景，1900年至2020年5月共记录到5.0级及以上地震158个，震中集中分布在普昌断裂附近区域。

受地理位置所限，柯坪块体所辖地震台站分布不均，南北跨度小，东西跨度大(图 1)，很多地震为偏网地震或发生在中国边境的网外地震，这增大了准确地震定位的难度。

2 数据来源

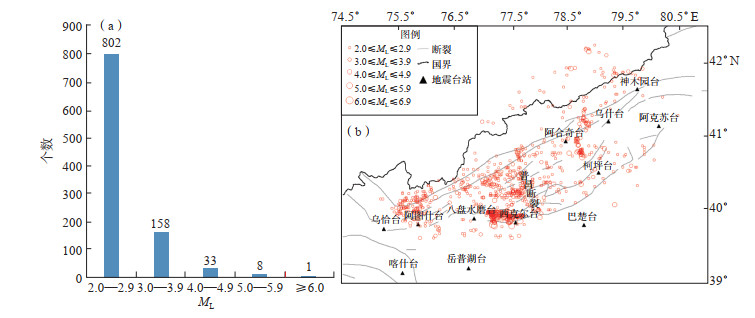
选取2018年6月至2020年5月新疆地震台网记录到的研究区M_L≥2.0地震的P波到时数据。因人工拾取的震相数据可能存在错误或误差较大等问题，故先拟合P波和震中距的时距曲线，再根据时距曲线来剔除明显的异常数据。根据经验设置阈值为5 s，剔除走时和时距曲线差值超过5 s的异常数据，并保留大部分数据(图 2)。由图 2可见，筛选后的走时—震中距间呈近似线性关系。选取至少有3个台站记录的地震事件，最后得到符合条件的地震事件共1 002个，其中，2.0≤M_L≤2.9事件802个，3.0≤M_L≤3.9事件158个，4.0≤M_L≤4.9事件33个，5.0≤M_L≤5.9事件8个，6.0≤M_L≤6.9事件1个(图 3)，地震震中主要分布在普昌断裂附近区域。数据主要来自新疆地震台网，主要包括巴楚地震台、柯坪地震台、阿图什地震台等12个固定台站的数据(表 1)。

由于S波到时比P波到时晚，且其首段覆盖在P波到时的尾端当中，这使得S波到时的误差高于P波到时，因此，仅采用P波到时数据用于速度结构校正和地震定位。

3 Velest反演原理

假定地震波走时为t_obs，它与台站坐标s、震源参数h、速度模型m间满足如下非线性关系

$ t_{\mathrm{obs}}=f(s, h, m) $

(1)

其中，地震波的到时和台站信息已知，震源参数和速度模型在一般情况下是未知的。为了求解上述方程，需要引入一个较合适的一维速度结构模型，以根据射线追踪理论计算地震波的理论计算走时t_cal。对式(1)作一阶泰勒展开，获取走时残差t_res、速度模型校正、震源校正之间的线性关系，得到如下方程

$ t_{\mathrm{res}}=t_{\mathrm{obs}}-t_{\mathrm{cal}}=\sum\limits_{k=1}^4 \frac{\partial f}{\partial h_k} \Delta h_k+\sum\limits_{i=1}^n \frac{\partial f}{\partial m_i} \Delta m_i+e $

(2)

其中，h为震源参数向量；m为速度模型参数向量；e为误差向量。在矩阵中，耦合震源参数模型中的参数关系式可以写成

$ \boldsymbol{t}=\boldsymbol{H} \boldsymbol{h}+\boldsymbol{M m}+\boldsymbol{e}=\boldsymbol{A d}+\boldsymbol{e} $

(3)

式中，t为走时残差矢量；H为矩阵走时相对于震源参数的偏分矩阵；h为震源参数校正向量；M为矩阵走时相对于速度模型参数的偏分矩阵；m为速度模型参数校正向量；e为走时误差矩阵，包括观测到的到时读取误差、台站位置坐标导致的误差、速度模型参数不精确及近似线性处理造成的误差；A为所有偏分矩阵；d为速度模型与震源参数校正矩阵。

在标准地震定位中，速度参数是固定不变的先验值，走时残差通过对4个震源参数的不断扰动和调整最终达到最小化。精确的地震定位及误差估计需要速度与震源参数的联合反演。

在线性化假设成立的情况下，通过选择真实模型领域中的起始模型，可以明显提高使用式(3)成功估算真实模型的机会。本文考虑的落脚点是一维速度模型，它本身就代表了式(3)中的最小二乘解。不仅用于开发一维模型的算法得到了充分研究，而且模型空间的较小维度使得计算全套线性诊断的实用性更强，故将这个最佳一维模型称为最小一维模型。

4 利用Velest算法反演最小一维P波速度模型 4.1 选取先验一维速度模型和反演结果

在使用Velest算法反演最小一维速度模型时，最初的震源参数和速度结构都是未知量，这就需要引入一个合适的速度模型作为先验模型。考虑到先验模型精准度对速度模型反演的影响，且目前新疆地震台网常规地震定位时使用的一维速度模型主要是“3400走时表”，所以选取3个不同的速度模型作为先验模型。这3个模型分别是“3400走时表”速度模型(模型一)(陈向军等，2014)、二层地壳速度结构新模型(模型二)(陈向军等，2018)、新疆地区地壳平均速度模型(模型三)(陈向军等，2018)[图 4(a)]。在反演过程中，当计算满足所有地震走时均方根残差(RMS)明显减小及台站校正值、速度值变化微小时即停止迭代。对3种不同的初始速度模型分别进行9次迭代，获得的输出速度模型如图 4(b)所示。由图 4(b)可见，模型一的走时均方根残差从1.369 943降到了0.364 242；模型二的从1.583 173降到了0.755 657；模型三的从1.228 390降到了0.583 064。由图 4(b)可见，经“3400走时表”速度模型校正后得到的速度模型与初始模型相差不大，在22—57 km处v_P比初始模型的略大，莫霍面v_P速度又比初始模型的略小。由模型二、模型三校正后的模型与初始模型相比，整体差异较明显，由模型二得到的校正速度模型在0—26 km处v_P比初始模型的明显增大，且能够看到低速层。由模型三得到的校正速度模型v_P在很大程度上比初始速度模型的偏小；同样，在初始速度模型中没有明显的低速层，而在校正后的结果中能够看到明显的低速层。

4.2 台站校正值

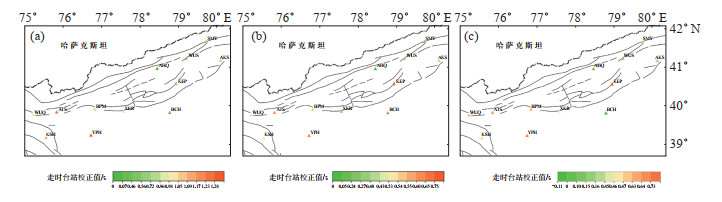
获得的台站校正结果如表 2所示，图 5为台站校正信息渐变图。由表 2可见，模型一的校正范围为0—1.28 s；模型二的为0—0.75 s；模型三的为-0.11—0.73 s。对于所有台站，模型一和模型二均呈现出正校正；模型三除了对巴楚地震台(BCH)呈现负校正外，对于其他台站均呈现正校正。

4.3 定位结果

重新定位前后走时均方根残差(RMS)结果显示(图 6)，原始数据走时均方根残差为0.1—1.4 s，峰值在0.9 s附近。重新定位后，模型一RMS为0.1—0.9 s，峰值在0.3 s附近，整体向0.1 s偏移；模型二RMS为0.1—1.5 s，峰值在0.5 s附近；模型三RMS为0.1—1.0 s，峰值在0.4 s附近。

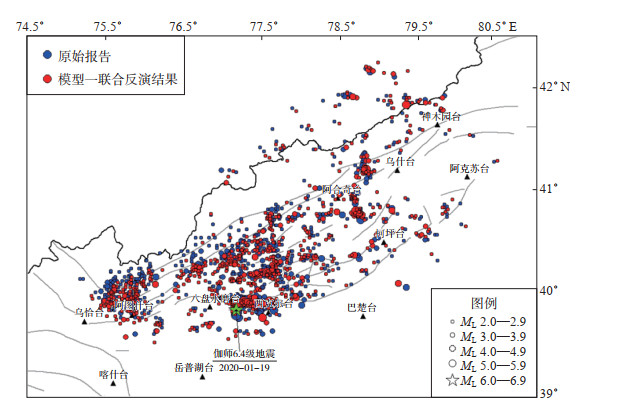
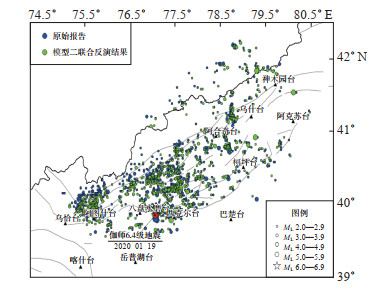
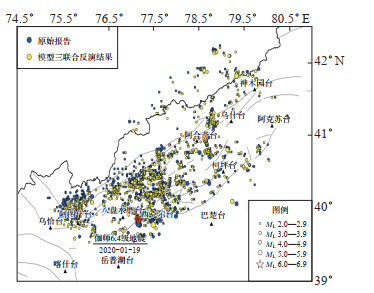
由3种模型联合反演获得的重新定位结果和原始报告中的震中位置可见(图 7—9)，重新定位后震中位置在空间上更加收敛，分布更集中，簇状分布更明显，尤其是在2020年1月19日伽师6.4级地震余震区更为明显，SN方向明显收敛，余震序列主要呈EW向分布，与柯坪断裂西段的几何位置较一致；由3种模型联合反演获得的重新定位震中位置差别不大。

由3种模型联合反演获得的震源深度和原始报告中的震源深度可见(图 10)，初始震源深度在5—8 km处较集中，重新定位后震源深度近正态分布，尤其是利用模型一反演后，震源深度分布更加均匀，在18—22 km处较集中。

5 结论

通过对柯坪块体进行最小一维速度模型初步反演发现，不同的先验模型反演出的最小一维速度模型存在差异，但使用最小一维速度模型对柯坪块体地震重新定位后地震走时残差有了较大幅度的降低。分析认为，应用最小一维速度模型重新定位使柯坪块体地震定位质量有了一定提高。

(1) 在3个不同的先验速度模型中，“3400走时表”速度模型校正后所得的速度模型与初始模型相差不大；二层地壳速度结构新模型(模型二)(陈向军等，2018)、新疆地区地壳平均速度模型(模型三)校正后的模型与初始模型间整体差异较明显，初始速度模型中没有明显的低速层，而在校正后的结果中能够看到明显的低速层。根据胥颐(1994)对新疆天山及邻区地壳上地幔三维速度的研究可知，柯坪块体存在低速区，本文研究结果与其较吻合。

(2) 台站校正值可以将浅层介质横向不均匀性对反演结果的影响归结到台站校正项上，反映了速度模型与真实模型之间的差异。校正值为负的台站为高速异常，校正值为正的台站为低速异常(Musumeci et al，2003)。利用3种模型进行台站校正基本为正校正，且以普昌断裂为界，东西两侧呈现出明显差异，普昌断裂西侧的台站校正程度均大于普昌断裂东侧。

(3) 使用最小一维速度模型重新定位的走时均方根残差(RMS)显著降低，且由“3400走时表”反演出的最小一维速度模型重新定位的RMS最小，表明模型一反演出的最小一维速度模型与真实模型更为接近。

(4) 由3种模型联合反演重新定位结果可见，重新定位后震中位置在空间上更加收敛，分布更集中，簇状分布更明显。震源深度趋于正态分布，尤其是利用“3400走时表，反演后的震源深度分布更加均匀，在18—22 km处较集中。