地震是一种破坏性极大的自然现象,给人类带来巨大的经济损失,在经济、交通发达的地区,震后应急救援工作尤为重要(陈钢铁等,2012;何珊珊等,2016;孙华丽等,2018)。为了完善震后应急救援工作机制,首先要明确震后救援特点。首先,要考虑救援物资的配送问题,它是指在地震发生后,在有限的时间、空间以及资源供给的情况下,采取适当方法,将救援人员以及各种救援物资快速、有效地配送到各受灾地区。然而,各地应对突发事件的物资储备一般是少量的,且不具备针对性,因此政府和各级部门需要在短时间内完成物资的整合和调度,使不同种类的救援物资能够从分散的配送中心运送至各个受灾点,迅速解决灾区的应急物资需求问题(徐琴,2008;魏航等,2009;周苹,2009;杨洋,2014)。其次,需考虑救援车辆路径规划问题。任何救援均建立在可达性基础上,若救援力量不可达,则救援决策将无法施行(杨成令,2020)。因此,需要决策者采取一种科学、切实可行的方式,规划并寻找合理的应急救援路线。运用科学的规划方法,在最短时间内,以最安全的方式将地震应急救灾物资分发到各受灾地区,从而最大程度地保障人民的生命财产安全,减少地震灾害损失,降低危害后果(郑斌等,2014;高鸿鹤等,2014;楼振凯,2017;宋英华,2018)。
本研究拟设计一种基于Dijkstra算法的多应急配送中心、多应急需求点震后路径规划软件。该软件以配送时间最短为目标,在考虑最短时间与最优公平性的应急物资调度基础上,同时考虑震后次生灾害对路网结构的影响,合理规划路径,并能实时反映各个车辆的预定轨迹和所处位置,根据路况信息实现对车辆行驶路径的后续规划。
1 算法简介Dijkstra算法由荷兰计算机科学家狄克斯特拉于1959年提出,是解决最短路径问题的经典算法之一,具有简单、快速、直观等优点,在网络路由、地图导航、物流配送等领域应用广泛。其主要特点是,以起始点为中心逐步向外扩展,直至搜索到全部节点为止,通过记录与该节点最近的前驱节点而生成集合,凭借集合中的各个向量,从而确立由起始点至目标点的最短路径。其核心思想是贪心算法。贪心算法是指在问题求解时,不从整体最优进行考虑,而是做出在当前看来是最好的选择,也就是某种意义上的局部最优解。因此,在使用Dijkstra算法时,连通图中的路径一定要有权值且不能为负。
2 模型构建 2.1 问题描述假设有多个地震应急物资配送中心(救援点),位置已知、物资量库存已知,这些点分别拥有应急配送车辆用来承担应急救援配送任务,同时有多个位置已知、需求量已知物资需求点(受灾点)。在满足一系列约束条件的情况下,确定配送路线,使所有受灾点的物资需求得以满足,并使地震应急救援物资配送至各个受灾点的时间之和最小。
2.2 基本假设构建模型的基本假设如下:①地震应急物资配送中心(救援点)数量、位置、库存量已知;②物资需求点(受灾点)位置、物资需求量已知;③参与救援的救援车辆均从救援点出发;④参与救援的救援车辆携带物资量不能超过其运输能力;⑤救援车辆支援各受灾点的每类物资数量不能超过该类物资在救援点的的库存量;⑥路线中所有节点间的距离已知。
2.3 影响因素一般来说,车辆的行驶时间可按照里程除以车速计算得出。由此可知,距离和车速对行驶时间有较大影响。在构建模型时,必须充分考虑所在区域发生次生灾害的可能性,但并不能确定是否实际发生,因此需要假定震后次生灾害在一定程度上会影响车辆的行驶速度,但这种影响大小取决于道路自身条件、地震发生时间、震级、道路两旁建筑物具体情况以及避难人群影响等因素(肖博,2019)。另外,在选择影响因素时,需要根据实际情况尽可能全面考虑对震后通行速度有影响的所有因素,且选择的影响因素要相互独立。综上,本研究假设救援车辆在执行救援任务期间主要受到以下5个因素的影响。
(1) 道路类型。一般情况下,不同的道路类型拥有不同的道路基础设施状况。其受地震影响的大小与原始道路等级成反比,道路等级越高,其受地震影响的程度越小。根据研究区内道路现状,将道路分为高速国道(G开头)与高速省道(S开头)2类,并提出影响系数l1,见表 1。
| 表 1 道路类型对车辆通行速度影响系数 Table 1 Coefficient of influence of road type on vehicle traffic speed |
(2) 路段长度。随着路段长度的增加,不可控因素随之增加,被地震波及的可能越大。基于以上分析,本研究将路段长度作为通行速度的影响因素,并给出其相应影响系数l2,见表 2。
| 表 2 路段长度对车辆通行速度影响系数 Table 2 Coefficient of influence of road section length on vehicle traffic speed |
(3) 地震发生时间。地震发生在白天和夜间,其影响程度有所不同,主要表现为:白天,特别是上下班高峰期,车辆较多,可能引发一些无法预料的交通事故;夜间,车辆较少,但是司机视线会受到影响,车速也会相应较低,影响救援效率。因此,本研究将地震发生时间作为通行速度的影响因素,并给出其相应影响系数l3,见表 3。
| 表 3 地震发生时间对车辆通行速度影响系数 Table 3 Coefficient of influence of earthquake occurrence time on vehicle traffic speed |
(4) 高程。高程即某一点沿铅垂线方向到绝对基面的距离,其对降雨量、植被类型及植被覆盖率有一定影响。随着高程的增加,降水量可能减少,植被覆盖率可能会降低,且植被可能由森林变为灌木、草地等,进而间接影响震后次生灾害的发生。正常情况下,高程差越大,坡度越陡,震后发生滑坡、崩塌等次生灾害的可能性越大。因此,将高程作为通行速度的影响因素,结合研究区域高程数据,给出其对应影响系数l4,见表 4。
| 表 4 高程对车辆通行速度影响系数 Table 4 Coefficient of influence of elevation on vehicle traffic speed |
(5) 峰值加速度。峰值加速度是指地震震动过程中,地表质点运动的加速度最大绝对值,可作为确定烈度的依据。其大小可表示为地震时建筑物受到最大地震作用力的大小,该值越大,表明建筑物的潜在可能受损程度越大。因此,将峰值加速度作为通行速度的影响因素,结合研究区域峰值加速度数据,给出其对应影响系数l5,见表 5。
| 表 5 峰值加速度对车辆通行速度影响系数 Table 5 Coefficient of influence of peak ground acceleration on vehicle traffic speed |
值得一提的是,为减小计算量且方便得到一组最优解来展示路况变化对路径规划的影响,本研究未采用启发式算法将车辆通行速度和道路安全情况作为多目标化问题进行求解,而是采用加权法,将多目标问题转化为单目标问题再进行求解,即对所有的目标函数通过设置相应的权重系数,将其线性组合为一个单目标函数的方法(Cohon,1978)。假设某一单目标函数为g(x),则有
| $g(x)=\sum\limits_{i=1}^n \omega_i f_i(x) $ | (1) |
式中,ωi为权重系数,fi为多目标函数。在本研究中,震后车辆通行速度和道路安全情况均作为一个影响速度的权重系数进行计算。时间预测公式可表示为
| $ T_{i j}=\frac{E_{i j}}{v_{i j}^1 \cdot l_1 l_2 l_3 l_4 l_5}+\frac{F_{i j}}{v_{i j}^2 \cdot l_1 l_2 l_3 l_4 l_5} $ | (2) |
| $ S_{i j}=E_{i j}+F_{i j} $ | (3) |
式中:Tij为在节点i到节点j路段Rij上的预测行车时间;Sij表示路段Rij的实际长度;Eij、Fij指路段Rij中高速国道、高速省道的长度;
设地震应急物资配送至各受灾点的总时间最短,则目标函数公式如下
| $ g=\min \sum\limits_{i=1}^M \sum\limits_{j=1}^N \sum\limits_{k=1}^K x_{i j k} T_{i j} $ | (4) |
其约束条件如下
| $ T_{i j}=\frac{E_{i j}}{v_{i j}^1 \cdot l_1 l_2 l_3 l_4 l_5}+\frac{F_{i j}}{v_{i j}^2 \cdot l_1 l_2 l_3 l_4 l_5} \quad T_{i j} \geqslant 0 $ | (5) |
| $ S_{i j}=E_{i j}+F_{i j} \quad S_{i j} \geqslant 0, E_{i j} \geqslant 0, F_{i j} \geqslant 0 $ | (6) |
| $\sum\limits_{j=1}^N x_{i j k} \leqslant q_{i k} \quad \forall i \in M, k \in K $ | (7) |
| $ \sum\limits_{j=1}^N \sum\limits_{k=1}^K x_{i j k} \leqslant D_i \quad \forall i \in M $ | (8) |
| $ Q_{j k} <\sum\limits_{i=1}^M \sum\limits_{k=1}^K x_{m n k} \leqslant\left(1+\alpha_{j k}\right) Q_{j k} \quad \forall j \in N $ | (9) |
其中:式(5)表示车辆在路段上的消耗时间;式(6)表示路段长度等于高速国道、高速省道之和;式(7)表示救援车辆支援各受灾点的每类物资量不能超过该类物资的库存量;式(8)表示参与救援的救援车辆携带物资量不能超过其运输能力;式(9)表示受灾点获得的物资满足其需求量。
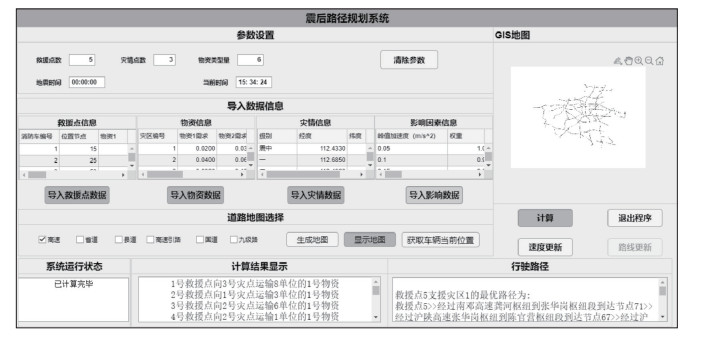
3 软件设计文中模型问题属于整数线性规划问题,问题规模较小,软件主要采用Matlab 2021b完成开发,结合YALMIP工具包以及CPLEX求解器进行小规模精确求解。软件主界面见图 1。
|
图 1 软件主界面 Fig.1 The main interface of the software |
该软件设置5个功能模块。模块1:参数设置。包含救援点数量、灾情点数量、物资类型数量、地震发生时间以及当前时间,其中当前时间根据计算机时间实时变化,且救援点、灾情点和物资类型数量需与模块2导入数据信息各点的数量一致。
模块2:导入信息数据。该模块包含4个部分,分别为“Excel”格式的救援点数据、物资信息、灾情信息、影响因素信息。其中救援点数据为全部救援点信息节点以及相应物资储备量和运输能力;物资信息为各受灾点各物资类型的需求量以及相应裕度值;灾情信息为各受灾点的节点编号;影响因素信息为设置的各类影响因素在相应区间范围的权重。
模块3:道路地图选择。该模块通过选择“shp”格式的各道路类型生成地图,在右侧GIS地图中完成显示,用户可参考实际路网信息建立研究区域节点路网。
模块4:计算功能。该模块包含计算并获取车辆实时位置、速度更新、路线更新4个部分。其中:计算部分根据模块1、2提供的信息直接对节点进行路径规划;获取车辆实时位置部分根据已消耗的时间信息、车速信息重新获取当前车辆位置;速度更新部分为地震发生后,路网中道路条件和行车条件可能有所改变,导致救援车辆在每一路段上的行驶速度发生变化,需根据实际情况进行速度更新,例如:当某一路段遭到破坏时,该路段的行驶速度应为0 km/h;路线更新部分则是在速度更新基础上重新对路径进行规划。
模块5:结果显示。该模块包含系统运行状态、计算结果显示、行驶路径信息3个部分。其中系统运行状态部分用于指引操作、观察软件运行状况;计算结果显示部分展示物资分配结果;行驶路径部分展示车辆路径信息以及车辆当前位置(图 2),方便用户管理查看。

|
图 2 软件运行结果示例 (上图为直接计算后的结果;下图为更新速度后车辆所在当前节点信息) Fig.2 Example of calculation results |
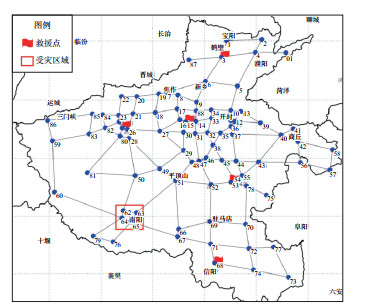
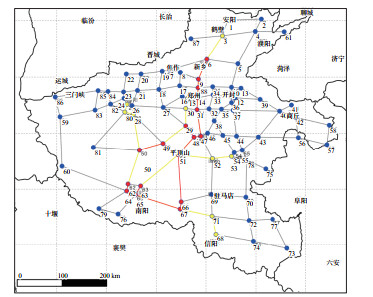
为了测试震后路径规划软件设计的有效性,以河南省作为研究区,将郑州、洛阳、鹤壁、信阳、周口地震监测中心站所在地市作为地震应急物资配送中心(救援点),并假设南阳地区在16时50分发生强震,有3处为受灾点,将路网信息中的节点进行编号,其节点与路段的位置示意见图 3。如图所示,救援点分别为节点3、节点15、节点25、节点53、节点68,受灾点分别为节点62、节点63、节点64。车辆行驶速度在高速国道上取值100 km/h,高速省道上取值80 km/h。各受灾点物资需求见表 6,救援点物资储备量见表 7。河南省高程及峰值加速度分布见图 4。
|
图 3 河南省高速公路各节点示意 (图中红旗代表救援点,红框代表受灾区域) Fig.3 Display of various nodes of Henan provincial expressway |
| 表 6 受灾点物资需求 Table 6 Demand for materials at disaster areas |
| 表 7 救援点物资储备 Table 7 Inventory of materials at rescue area |
|
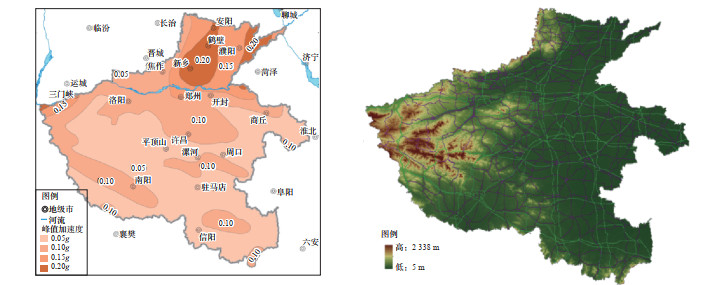
图 4 河南地区峰值加速度与高程分布 Fig.4 Peak ground motion acceleration and elevation distribution in Henan region |
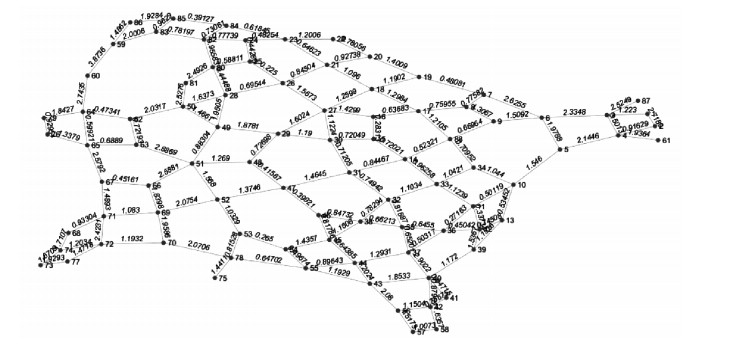
将各类影响因素带入计算,可得各节点之间通行时间,具体数据见图 5。确定这些路段的通行时间,可将不同时刻震后路网的动态变化问题转化为一系列离散时间节点的静态决策问题。
|
图 5 各节点间通行耗时 Fig.5 Travel time between nodes |
据相关假设,软件运行结果如下:
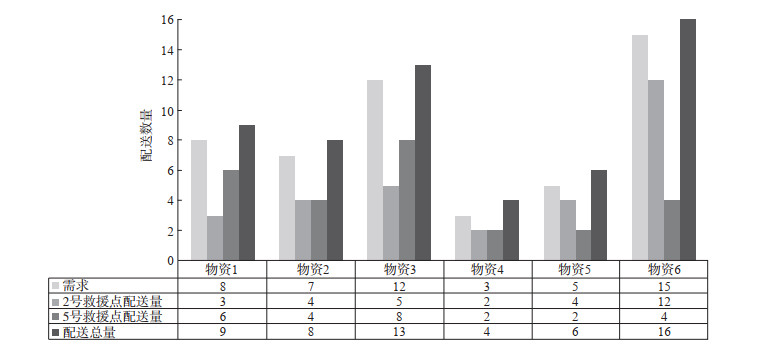
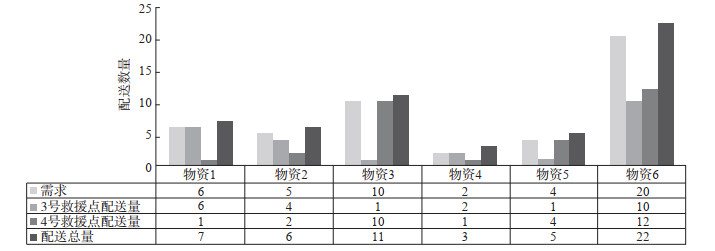
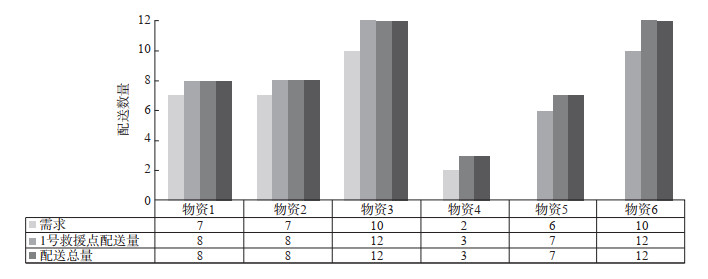
(1) 物资配送结果。1号救援点前往3号受灾点:配送8单位1号物资、8单位2号物资、12单位3号物资、3单位4号物资、7单位5号物资、12单位6号物资;2号救援点前往1号受灾点:配送3单位1号物资、4单位2号物资、5单位3号物资、2单位4号物资、4单位5号物资、12单位6号物资;3号救援点前往2号受灾点:配送6单位1号物资、4单位2号物资、1单位3号物资、2单位4号物资、1单位5号物资、10单位6号物资;4号救援点前往2号受灾点:配送1单位1号物资、2单位2号物资、10单位3号物资、1单位4号物资、4单位5号物资、12单位6号物资;5号救援点前往1号受灾点:配送6单位1号物资、4单位2号物资、8单位3号物资、2单位4号物资、2单位5号物资、4单位6号物资。其中1号受灾点需要2号、5号救援点共同配送,配送结果见图 6;2号受灾点需要3号、4号救援点共同配送,配送结果见图 7;3号受灾点仅需1号救援点完成配送,配送结果见图 8。各救援点物资配送数量均未超过车辆运输能力及库存数量,每个受灾点的配送总量均超过其需求量,满足配送要求。
|
图 6 1号受灾点物资配送结果 Fig.6 Results of material distribution in disaster area 1 |
|
图 7 2号受灾点物资配送结果 Fig.7 Results of material distribution in disaster area 2 |
|
图 8 3号受灾点物资配送结果 Fig.8 Results of material distribution in disaster area 3 |
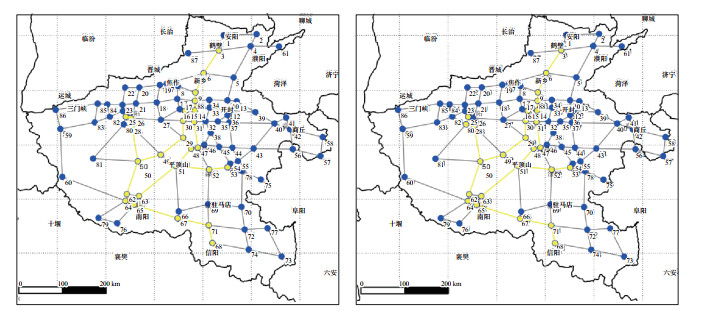
(2) 静态路径规划结果。5号救援点支援1号受灾点的最优路径为:节点68—71—67—65—64—62,车辆配送耗时6.07小时;4号救援点支援2号受灾点的最优路径为:节点3—6—9—88—14—31—47—48—51—63,车辆配送耗时11.92小时;3号救援点支援2号受灾点的最优路径为:节点53—52—51—63,车辆配送耗时5.48小时;2号救援点支援1号受灾点的最优路径为:节点25—26—28—50—62,车辆配送耗时4.59小时;1号救援点支援3号受灾点的最优路径为:节点15—30—29—49—50—62—64,车辆配送耗时7.76小时。配送路径见图 9(a)。
|
图 9 1—5号救援点配送路径 (图中蓝色圆圈代表各个节点,灰色曲线代表路网,黄色曲线代表路径规划后的路线)(a)加入影响系数;(b)未加入影响系数 Fig.9 Material distribution path of rescue point 1-5 |
以车辆通行速度和道路安全情况为目标构建影响路径选择的影响系数,其大小决定了路径规划算法的计算结果。若排除所有影响,计算得到的最优救援路径必定是行程最短路径,见图 9(b)。
由图 9可知,有影响因素与无影响因素的路径规划区别仅在于2号救援点支援1号受灾点节点25—26—28—50—62中,节点25—26路段变更为节点25—80路段。变更这一路段的原因在于高程因素占了较大比重。从安全角度看,模型考虑的各个影响系数在一定程度上对危险性较大的路径进行取舍。通过调节各个权重值,决策者可以在计算结果中选择耗时短且相对安全的路径,组织参与救援车辆开展灾后救援任务。
(3) 动态路线调整结果。根据地震灾害特点,静态路径规划已不能满足应急救援任务的需要。地震发生后,随着时间的推移,路网信息也在发生变化,同时受余震影响,原本可行部分路段被阻断,因此需要根据实时路况信息动态调整救援车辆行驶路线,也就是说,需要根据车辆位置信息对未行驶路线进行重新规划。
假设南阳地区16时50分发生地震,并在地震发生时刻完成静态路径规划。假设在1 h30 min后,节点50—62路段、节点51—63路段因余震发生断裂,使得原路线不可通行,需要及时调整路线,此时路网信息更新。
0时刻路径规划结果:救援点5:节点68—71—67—65—64—62;救援点4:节点3—6—9—88—14—31—47—48—51—63;救援点3:节点53—52—51—63;救援点2:节点25—26—28—50—62;救援点1:节点15—30—29—49—50—62—64。1 h30 min后,根据图 4所示各路段耗时,各救援点车辆当前位置信息如下:救援点5支援灾区1的车辆当前位于节点67;救援点4支援灾区2的车辆当前位于节点6;救援点3支援灾区2的车辆当前位于节点51;救援点2支援灾区1的车辆当前位于节点50;救援点1支援灾区3的车辆当前位于节点29。
路径重新规划结果(图 10):救援点5:节点67—65—64—62;救援点4:节点6—9—88—14—31—47—48—51—66—67—65—63;救援点3:节点51—66—67—65—63;救援点2:节点50—49—51—66—67—65—64—62;救援点1:节点29—48—51—66—67—65—64。
|
图 10 1—5号救援点路径重规划结果 (图中蓝色圆圈代表各个节点,灰色曲线为路网,黄色曲线为静态路径规划结果,红色曲线为路径重新规划后结果) Fig.10 Rescheduling results of route for rescue point 1-5 |
计算结果表明,重新计算得到的最佳路径成功避开了路段50—62、路段51—63(图 10),为救援车辆节省了宝贵时间。
4.3 实验总结以河南省作为研究区,选取郑州、洛阳、鹤壁、信阳、周口地震监测中心站作为地震应急物资配送中心(救援点),以南阳地区3处位置作为受灾需求点。使用该软件,首先,对初始阶段获取的路网信息、物资需求进行统计,设计初始阶段路径规划和物资分配方案。其次,根据车辆在配送过程中接收的新的路网信息重新对路径进行规划,使车辆绕开中断路径,顺利到达目的地。最终,运行计算结果达到软件设计初衷。相较于传统导航软件通过用户共享位置判断路段的通行时间和拥堵情况,本研究设计的软件可直接通过人工完成路网信息处理,且通过对各路段节点配置权重,从而更加全面地获取道路通行能力信息。同时,考虑到动态决策的快速决策要求,得到新的规划路径,以保证应急救援物资的及时供应。
5 结论地震应急救援是一项复杂的系统工程,将救援物资在最短时间送达灾区是其中重要的一个环节,保障应急救援物资的及时供应关系到人民的生命安全和社会稳定。因此,在地震发生后,快速、有效地进行震后救援工作对于减少人员伤亡、降低损失具有重要意义。本研究以Dijkstra算法为基础,设计一种震后路径规划软件,用来实现震后救援路径规划、物资最优分配以及路径重新调整等功能,可为震后救援人员提供高效、快捷、合理的规划服务,从而提高救援工作效率。
在本研究设计的软件中,影响因素部分采用加权法,其原理是,通过设置相应的权重系数,将所有目标函数进行线性组合,使其成为一个单目标函数。但是,各权重系数的选择均建立在对各指标充分了解的基础上。因此,需要用户针对实际情况,采取相应方法对权重系数进行慎重考虑。另外,软件实验所采用的震后应急路网模型相较于实际情况进行了简化,用户可增加路径节点建立丰富的路网模型,从而获得更加真实的结果。
该软件采用较经典的Dijkstra算法,在实际应用中可能由于模型较大而遇到一些问题,例如:搜索空间过大、搜索时间过长、容易陷入局部最优等。在后续研究中,将进一步完善该软件功能,并对其进行测试验证。
陈钢铁, 帅斌. 震后道路抢修和应急物资配送优化调度研究[J]. 中国安全科学学报, 2012, 22(9): 166-171. |
高鸿鹤, 唐辰. 基于配送时间最短的应急物流路径规划[J]. 物流工程与管理, 2014, 36(2): 75-78. |
何珊珊, 朱文海, 庄需芹. 基于灾害抢修的应急物资多阶段配送路径研究[J]. 计算机仿真, 2016, 33(3): 167-171. DOI:10.3969/j.issn.1006-9348.2016.03.036 |
楼振凯. 应急物流系统LRP的双层规划模型及算法[J]. 中国管理科学, 2017, 25(11): 151-157. |
宋英华, 宁晶婧, 吕伟, 等. 震后初期应急物流公私协同的动态LAP模型[J]. 中国安全科学学报, 2018, 28(3): 173-178. |
孙华丽, 曹文倩, 薛耀锋, 等. 考虑路径风险的需求不确定应急物流定位-路径问题[J]. 运筹与管理, 2018, 27(7): 37-42. |
魏航, 魏洁. 随机时变网络下的应急路径选择研究[J]. 系统工程学报, 2009, 24(1): 99-103. |
肖博. 基于多目标优化的震后应急物流路径规划研究[D]. 西安: 长安大学, 2019.
|
徐琴. 突发公共事件应急物流系统优化中的定位—路径问题研究[D]. 成都: 西南交通大学, 2008.
|
杨成令. 震后基于时空网络的救援车辆路径优化模型研究[D]. 武汉: 武汉理工大学, 2020. DOI: 10.27381/d.cnki.gwlgu.2020.000302.
|
杨洋. 城市突发事件应急物流定位—路径研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
|
郑斌, 马祖军, 李双琳. 基于双层规划的震后初期应急物流系统优化[J]. 系统工程学报, 2014, 29(1): 113-125. |
周苹. 应急救援物资配送车辆路径选择问题的研究[D]. 哈尔滨: 哈尔滨工业大学, 2009.
|
Cohon J L. Multi-objective programming and planning[M]. New York: Academic Press, 1978.
|
 2024, Vol. 45
2024, Vol. 45


