0 引言

地铁运行时的杂散电流会造成地电场观测数据突跳，干扰幅度可能达到地电场正常日变化幅度的十几倍，严重影响数据的可用性。随着我国轨道交通的发展，受到影响的地电台站逐渐增多，如何提高地电观测数据质量，是当下亟待解决的问题。安张辉等（2011）、冯红武等（2019）利用经验模态分解剔除地铁干扰；王同利等（2013）利用低频滤波消除干扰成分。这些方法基于频率特征进行滤波，对于改善数据质量有一定作用，但也存在一定局限。地铁干扰与地电场观测研究频段有部分交叉，干扰数据的优势频段与列车运行速度、方向、车站间距等因素有关，而经验模态分解每阶本征模态函数（Intrinsic Mode Functions，简称IMF）的物理意义并不明确（汤井田等，2012；席继楼，2019）。

数学形态学是一种处理非线线性信号的分析方法，1964年由法国数学家Matheron和Serra共同创立（Matheron，1975；Serra，1983）。其基本思想是设计一个结构元素，利用该元素对信号的几何特征进行修正，以达到降低噪声的同时保留有用信息的目的。数学形态学基本变换包括腐蚀和膨胀运算，前者用来剔除观测序列边界不平滑的凸起，后者用来填平边界不平滑的凹陷。数学形态学滤波用于矿集区强干扰背景下，消除大地电磁探测数据中的各种三角波、脉冲波和其他工频噪声，针对不同频率采集的数据均取得较好的去噪效果（汤井田等，2012；李于波等，2022），也为消除地电场观测时间序列中的地铁干扰提供了一种新的思路。

由于武汉地铁工程的实施，武汉基准地震台（九峰）电磁观测项目的观测环境遭到破坏，经中国地震局批示，湖北省地震局将电磁测项整体搬迁至应城市汤池镇。应城地震监测站2015年竣工，2016年完成仪器安装调试，2018年正式开始地电场观测。2021年11月起，应城地电场每日同时段受到干扰，结合同台观测的地磁数据进行分析，发现干扰源自武汉地铁6号线（张建涛等，2022）。作为湖北地球物理台网唯一的地电场观测台站，改善应城站地电场观测数据质量是必要的。本文分别利用均值滤波、模态分解和数学形态学滤波方法，对应城站电场观测数据进行处理，对比分析各种方法的处理效果和影响因素，以寻找适用的滤波算法和参数。

1 数据对比 1.1 日变化形态

应城站地电场观测仪器为ZD9A-2B型地电场仪，采样频率为1次/min。该站地电场3个测向长、短极距数据的相关系数均在0.99以上，限于篇幅，文中仅选择长极距NS测道数据进行分析。

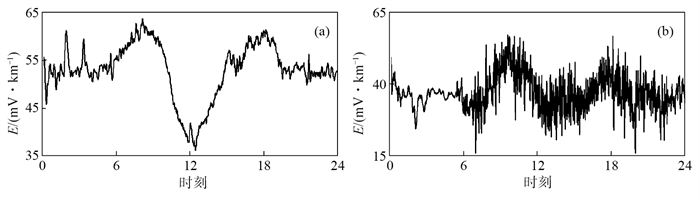
图 1(a)示出应城站地电场正常观测曲线，可见北京时间20时至次日6时呈近似直线，其他时段呈“两峰一谷”正弦曲线形态，属于TGF-B型地电场，NS测向长极距日变化幅度约为15—30 mV/km（谭大诚等，2010；张建涛等，2022）。图 1(b)示出应城站地电场地铁干扰数据曲线，可见6—22时出现扰动突跳，地电场日变幅度增大。

距离地铁越近，地电场观测受到的干扰幅度越大，如武汉九峰地电场地铁干扰幅度为应城的10倍以上，观测数据已不可用。由图 1(b)可见，应城地电场受干扰数据仍可分辨地电场日变形态，但信号的细节特征被地铁干扰所掩盖，且若存在高压直流输电干扰和电磁暴引起的地电场数据变化，因其干扰幅度较低，均可能被地铁干扰背景所掩盖。

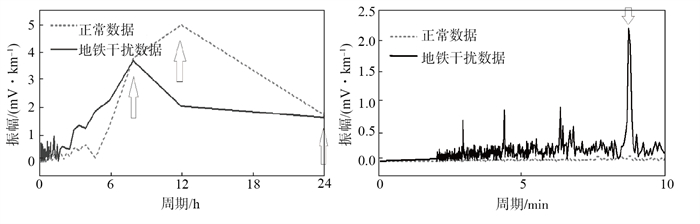
1.2 时频特征

在地电场观测数据日变化形态（图 1）上，不能明显看出地铁干扰与正常数据的本质差异，采用快速傅里叶变换（Fast Fourier Transform，FFT）方法，分析二者功率谱分布特征，发现2种数据的幅度差异主要体现在短周期（图 2）。对于未受干扰的地电场数据，幅度最大的傅里叶谐波周期依次是12 h、8 h和24 h，周期在0—10 min，谐波幅度可忽略不计；而受到地铁干扰的地电场数据前3阶谐波周期分别是8 h、6 h和8.7 min，其次是周期为12 h的半日波和周期为24 h的全日波。二者在中长周期的幅度差别不大，在周期0—10 min的傅里叶谐波中，受干扰数据的幅度达到正常数据的20倍以上。

1.3 干扰幅度

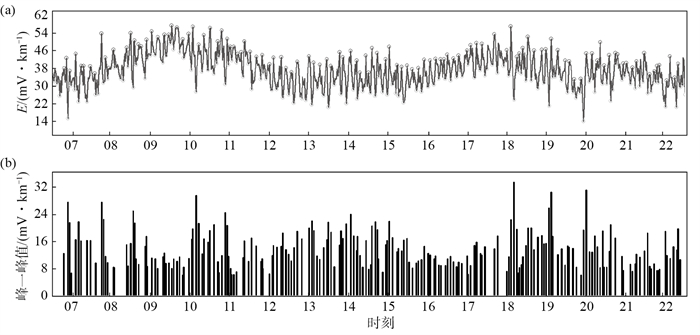
地铁对地电场的干扰方向和幅度呈规律性变化，在达到一个正的极大值之后方向反转，逐渐达到一个负的极小值。为定量分析地铁干扰的变化特点，对正负极值点进行提取，计算峰—峰值干扰幅度，结果见图 3。

可以发现，地铁对地电场的干扰幅度是变化的，如2021年12月26日平均峰峰值幅度为13.6 mV/km，最大峰峰值幅度为33 mV/km。当日7—9时、10—11时、18—20时干扰幅度较大，与工作日早晚上下班高峰时间对应，15—17时干扰幅度较小，应与人流量大小和发车间隔有关。

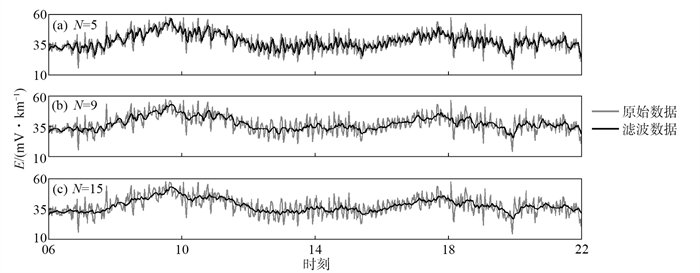
2 传统滤波方法 2.1 均值滤波

均值滤波是将N个取样步长内的采样值取平均值，对于高频振动的周期性干扰有良好的抑制作用。地铁对地电场的干扰表现为周期性高频突跳，因此可以采用均值滤波来提高数据质量。文中将N分别取为5、9和15，滤波前后数据对比曲线见图 4。

试验表明，均值滤波结果与窗口长度N有关，N取值越大，去除突跳的效果越显著。但是均值滤波会导致数据在时间上滞后，N取值越大滞后量越多，因此N的取值必须具有适用性。对于应城站地电场当前干扰水平，N取值为15时能够去除比较明显的突跳干扰。均值滤波会受到数据中极值的影响，干扰幅度较小时滤波效果较好，而当地铁干扰幅度大时滤波效果不佳。如图 4所示均值滤波曲线，15—17时地铁干扰幅度较小，滤波后该时段数据曲线平滑。

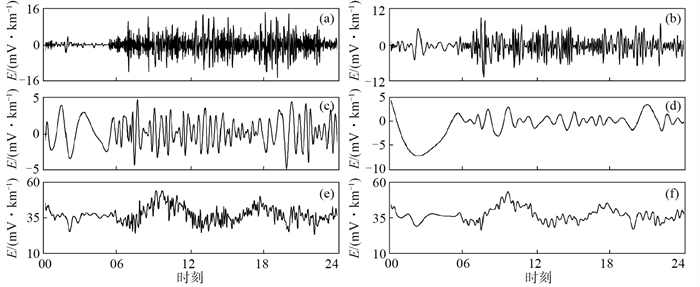
2.2 经验模态分解

经验模态分解（Empirical Mode Decomposition，EMD）是将复杂信号从高频到低频自适应分解为一系列具有不同时间尺度的模态函数（Intrinsic Mode Function，IMF）的方法（Huang et al，1998）。时频分析表明，地铁干扰属于高频干扰，理论上可以采用去除若干高频IMF分量，组合重构其余IMF分量的操作，以达到去除观测数据中地铁干扰成分的目的。按照以上思想，利用Matlab时频分析工具箱，对应城站2021年12月26日地电场数据进行分解，得到其IMF模态函数和一个残余分量，其中第1—4阶模态函数曲线见图 5(a)、(b)、(c)、(d)。

不难发现，第1阶模态函数由短周期突跳构成，在地铁运行时段，突跳频次和幅度均显著增大，表明地铁干扰主要存在于在1阶固有模态函数中，而第2阶模态函数曲线中也存在明显突跳成分，突跳幅度相对减小，周期增大。分别将2—8阶和3—8阶固有模态函数进行组合，重构之后的地电场信号见图 5(e)、(f)。在0—6时地铁停运时段，地电场观测应不存在地铁干扰，但重构后数据曲线与原始数据曲线存在差异，说明第1、2阶模态函数中包含地电场自身变化成分，即地电场自身与地铁干扰的频段存在交叉。

3 数学形态学滤波

形态结构因子是影响滤波效果的因素之一，常用结构元素有三角型、圆盘型、直线型和抛物线型等，也可以将2种结构因子进行级联组合，形成广义形态学滤波器（汤井田等，2012）。根据待处理信号中干扰噪声的形状不同，在处理时应选择合适的结构元素以达到削弱噪声的目的。

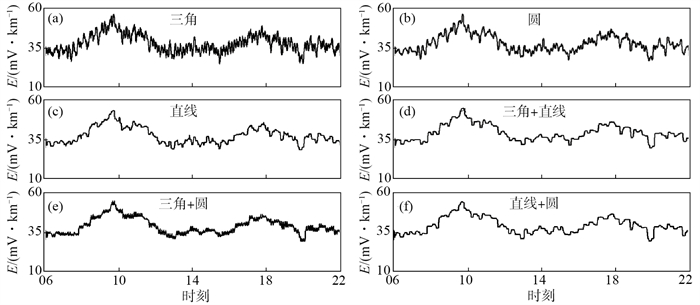
3.1 不同结构元素滤波效果对比

为了选择合适的地电场结构元素，分别采用宽度和幅度均为7的三角、圆和直线结构元素及其两两组合进行数学形态学滤波，结果见图 6。可以发现，三角形结构元素形态学滤波后的数据中依然存在密集突跳[图 6(a)]，使用圆形结构元素滤波后的突跳大幅减少[图 6(b)]，数据经直线结构元素滤波，仅剩余一些幅度较大的突跳干扰[图 6(c)]。使用直线和其他结构元素构建广义形态学滤波器，其滤波效果与单独使用直线形结构元素几乎相同，与直线形结构元素在滤波器中的先后顺序无关，见图 6(d)、(e)、(f)。

3.2 不同尺度结构元素的滤波效果

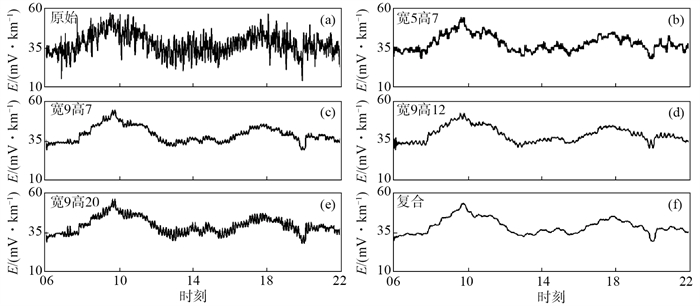
除了结构元素类型，其宽度和幅度也会对滤波结果造成影响。根据上一步试验结果，使用三角形和圆组成不同尺度的广义形态学滤波器，处理后的地电场观测数据见图 7。其中，图 7(b)表示形态学结构元素的宽度因子为5，高度因子为7，其余插图数值含义与此相同。

由图 7可知，形态学结构元素的宽度因子和尺度因子均会对地电场干扰数据的滤波结果造成影响。当尺度因子相同时，宽度因子越大则去除突跳的效果越显著[图 6(b)、(c)]。而尺度因子必须选择一个合适的值，其数值偏小[图 7(c)]或偏大[图 7(e)]均会削弱滤波效果。试验表明，当结构元素宽度为9、幅度为12时，地铁干扰去除效果较理想，再进行周期为9的均值滤波，得到的数据曲线更接近地电场正常变化形态。

4 结论与讨论

对比应城站地电场正常观测数据和受地铁干扰数据的差异，研究地铁运行对地电场干扰的时频和幅度特征，对比分析均值滤波、经验模态分解和数学形态学滤波去除地铁干扰的效果，得到以下结论：

（1）武汉地铁运行对地电场造成的干扰，在观测数据曲线上表现为正负交替变化的突跳，优势成分集中在周期为2—10 min的短周期成分上，但干扰频段不固定，采用模态分解方法不能有效区分地电场正常记录和干扰变化。

（2）地铁运行对地电场造成的干扰幅度并不固定。应城站地电场受到的地铁干扰平均幅度为14 mV/km，最大干扰幅度约33 mV/km，超过正常观测数据的日变幅度。

（3）通过均值滤波，可以改善观测数据质量，但地电场观测极值数据对滤波结果影响明显，当地铁干扰幅度较大时，该方法并不适用。

（4）地铁运行对地电场观测造成干扰，适宜采用三角和圆构建广义形态学滤波器进行滤波，但滤波效果与结构元素宽度和尺度因子有关，对于应城站，设置宽度因子为9、高度因子为12时，效果较好。

本研究结果可为受地铁运行困扰的地电场台站提供数据处理思路，但不同台站需根据自身情况对观测数据进行各种参数测试，以确定合适的滤波参数。