随着城市建设的发展,爆破事件逐渐增多,对地震记录造成显著干扰。爆破振动信号是一种典型的非平稳随机信号,往往受到地质地形条件、工程环境等因素的综合影响,含有较多高频噪声成分;同时,受到机械摆体的布朗热噪声、换能放大器和反馈网络电路电子噪声等地震计自身影响(刘洋君等,2010)。多因素综合作用导致采样信号失真,从而产生误差。常采用傅里叶变换、小波分解类方法(柳建新等,2006;饶运章等,2015)、经验模态分解类(EMD)及改进方法进行去噪。傅里叶变换需要信号的全部时域信息,有较大局限性;小波分解更适用于处理非平稳的爆破信号,但存在小波基选取难、分解层数确定难的缺点;希尔伯特—黄变换是一种经验数据分析方法,经验模态分解EMD,其扩展是自适应性的,可以用来描述非线性、非平稳数据的物理意义,但缺点是存在于模态混叠现象中,提取的IMF分量会被模态混叠污染(Huang et al,1998;Wu et al,2009)。
诸多学者将CEEMD和小波阈值法、LMD-MFE-SVD等方法联合使用,对含噪分量进行SVD滤波,得到更准确的爆破振动信号,为后续信号分析提供依据(周红敏等,2023;田婕等,2023)。小波类阈值和类经验模态分解EEMD、CEEMD等方法,在齿轮故障诊断、光电信号的分解重构应用中,效果较好(王红军等,2013;杨潞霞等,2016;陈真诚等,2019),本文将集合经验模态分解(EEMD)和小波阈值法结合起来,以互相关系数为特征选取指标,结合频谱特性去除噪声和趋势项,并重构信号,还原真实信息记录,以获取高质量数据。
1 爆破振动信号预处理方法 1.1 集合经验模态EEMD原理EMD分解得到的IMF分量往往存在模态混合,造成IMF分量不精确,Huang等(1998)认为,模式混叠是极值点的选择造成信号的间歇现象。为克服EMD的模态混叠,Wu等(2009)提出一种噪声辅助信号分析方法——集合经验模态分解(Ensemble EMD,EEMD)法,其本质是一种叠加高斯白噪声的多次经验模式分解。利用零均值噪声特性,对多次EMD得到的相应IMF分量进行总体平均以抵消加入的白噪声,从而有效抑制模态混叠的产生。
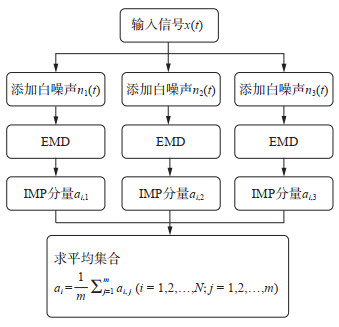
EEMD算法流程见图 1,具体步骤如下:①将一个具有标准正态分布的白噪声ni(t)加入原始信号x(t),产生一个新信号;②对加入白噪声的信号xi(t)进行EMD分解,得到各自的IMF分量;③步骤①和②重复进行m次,每次分解加入不同幅值的白噪声信号;④将所得IMF分量进行集成平均运算,得到EEMD分解的最终结果。计算公式如下
| $ a_i=\frac{1}{m} \sum_{j=1}^m a_{i, j} \quad(i=1, 2, \cdots, N ; j=1, 2, \cdots, m) $ | (1) |
|
图 1 EEMD流程 Fig.1 EEMD flow chart |
小波分析是一种时频分析方法,具有多分辨率分析特点,在时域和频域均具有表征信号局部特征的能力。对含噪信号进行小波分解,实际上是一个滤波过程,即对各个频段分别采用不同阈值进行处理,舍弃低于阈值的系数,对信号进行小波重构即可达到降噪目的。通常,真实信号表现为低频部分或较平稳部分,而噪声信号则表现为高频部分。
应用小波降噪可以较好地抑制信号中的无用部分、增强有用部分,其基本步骤为:小波分解—阈值处理—重构信号。小波基函数各有特点,在信号降噪处理过程中,没有任何一种小波基函数可以适应所有类型信号,本文结合爆破是非平稳随机信号的特点,选择具有紧支的db4小波基,分解4层;根据基于无偏风险估计原理确定阈值系数,以软阈值法去噪,对爆破数据进行分解重构。
小波去噪软阈值处理函数
| $ \sigma_\lambda(w)= \begin{cases}{[\operatorname{sgn}(w)(|w|-\lambda)]} & |w| \geqslant \lambda \\ 0 & |w|<\lambda\end{cases} $ | (2) |
式中:w为小波系数,λ为阈值。
1.3 集合经验模态EEMD——小波阈值降噪集合经验模态EEMD——小波阈值降噪具体步骤如下:①将爆破信号进行集合经验模态EEMD分解,分解为若干IMF信息分量;②趋势项处理:根据每个IMF与原信号的互相关函数值,作为初步筛选指标,确定并判断IMF包含的信号量是否参与信号重构;③对选取部分IMF分量进行FFT变换,验证其频幅曲线,辅助对照检查,防止遗漏有用信息,对其余IMF分量进行小波降噪处理;④完成降噪后进行波形重构;⑤计算信噪比SNR、互相关系数R,作为处理效果的衡量指标。
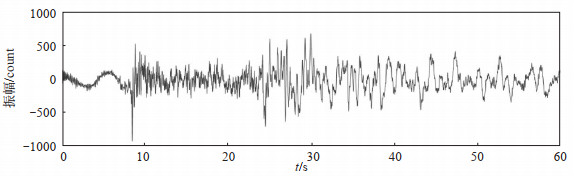
2 实例分析及效果评价2016年6月14日黑龙江省牡丹江地震台记录到附近某矿业公司ML 2.0爆破事件,选取甚宽频带CTS-1EF地震计垂直向数据记录(图 2)进行数据预处理和分析评价。
|
图 2 爆破信号 Fig.2 Blast signal |
使用Matlab软件的detrend函数对数据进行基线校正,消除线性漂移。设置白噪声标准差Nstd = 0.2,确定平均次数NR = 100,最大迭代次数MaxIter = 200,进行EEMD分解,得到12个IMF分量(IMF1—IMF12)和1个剩余分量Res,结果见图 3。

|
图 3 EEMD分解结果 Fig.3 EEMD decomposition results |
相关函数是描述2个信号X(s)、Y(t)之间相似性的一种度量,表征在任意2个不同时刻s、t的取值之间的相关程度。这2个信号可以是确定的,也可以是随机的,二者之间的相似性用相关系数大小来衡量,相关系数越大,相关性越大。
自相关函数是描述随机信号x(t)在任意不同时刻t1、t2取值之间的相关程度。定义式如下
| $ R(s, t)=E(X(s) \cdot X(t)) $ | (3) |
在信号处理中,用互相关来衡量2个信号x(t)和y(t)在2个不同时刻取值的相关程度。
对于连续函数,定义如下
| $ f(\tau) \cdot g(\tau)=\int_{-\infty}^{+\infty} f(t) g(t+\tau) \mathrm{d} \tau $ | (4) |
噪声具有随机性和时变性,含有噪声的爆破信号经EEMD变换后,所获得的IMF分量包含有效信息和虚假成分,当原始信号与IMF分量的互相关系数较大时为有效分量,反之则为虚假分量(张雪英等,2015)。通过确定各个IMF分量的相关度,可以提高降噪的准确度和精确度。
将已分解的爆破信号的IMF各分量与原始信号进行互相关运算,统计结果见表 1,可知IMF9、IMF10、IMF11、IMF12分量的互相关系数较小,初步认定其为含噪分量和趋势项分量。文中选取0.1作为经验指标,具体数值可在实践中调整和优化。
| 表 1 各IMF分量互相关系数 Table 1 Cross correlation coefficient of IMF components |
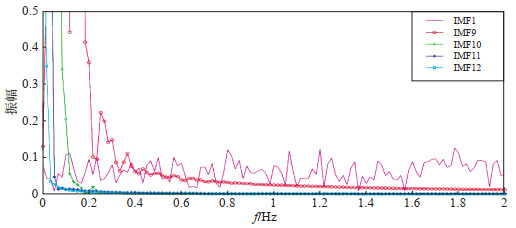
将IMF9、IMF10、IMF11、IMF12分量进行快速傅里叶变换,显示频率宽度较窄,集中于0—0.5 Hz低频段(图 4),表明4个分量可能是地震计的仪器响应及背景噪声,而非爆破信号成分,反映了仪器及背景噪声的变化趋势;对比互相关系数为临界值附近的IMF1分量,该分量频带明显较宽,其包括大部分频带范围,主频在有效监测范围内。因此,IMF9—IMF12分量可予以剔除。
|
图 4 疑似趋势项分量频谱 Fig.4 Spectrum diagram of suspected trend component |
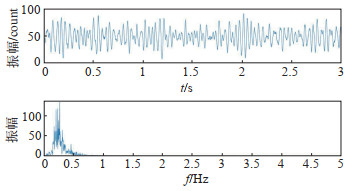
为检验该结论,选取同一地震计无地震或爆破干扰的平静时段数据,采用快速傅里叶变换绘制频幅图,截取其中平静时长300 s的数据频幅分析图,见图 5,可见地震计及周边背景噪声频率集中于0—0.5 Hz范围内,与IMF9—IMF12各个分量的频率范围一致,故可做分量去除。
|
图 5 平静时段数据FFT频幅图 Fig.5 FFT frequency amplitude diagram of data in aseismic period |
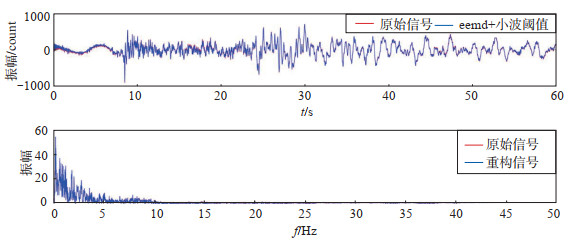
将IMF1—IMF8各分量进行小波阈值消噪后进行重构,原始信号与重构波形对比曲线见图 6。信号重构后消除了噪声干扰,特别是部分时段的尖峰幅值,保留了更多真实信息。爆破较天然地震的频带范围窄,频谱成分单一,能量释放较为集中,主要分布在4—7 Hz的低频区域(刘莎等,2012;费鸿禄等,2018;周少辉等,2021),且数值一般不会太大,信号去噪重构后,对于10 Hz以上的非爆破信号进行压缩降噪处理,FFT变换后,频率—振幅图显示,降噪效果明显。
|
图 6 IMF1—IMF8分量重构前后信号对比 Fig.6 Comparison of IMF1-IMF8 components before and after reconstruction |
将上述爆破信号分解重构后与原始信号进行对比,使用信噪比SNR和相关系数R作为检验指标,对重构效果进行评价。一般认为,SNR越大,相关系数R越接近于1,其处理效果越好。计算公式如下
| $ \mathrm{SNR}=10 \lg \frac{\sum_{t=1}^T x_i^2}{\sum_{t=1}^T\left(x_i-X_i\right)^2} $ | (5) |
检验结果见表 2,表明:采用EEMD与小波阈值的联合分析方法进行信号重构,信噪比更大,相关性更接近于1,重构效果优于单一方法。
| 表 2 效果检验 Table 2 Effect inspection |
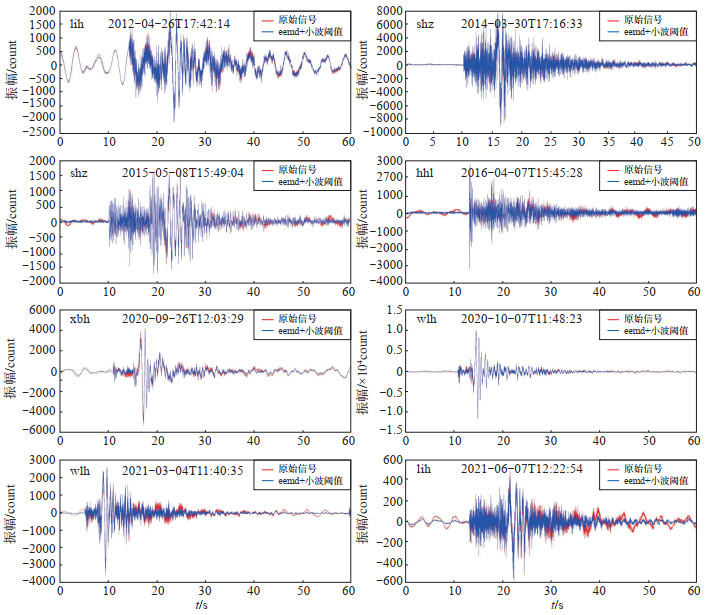
选取镜泊湖火山监测台网记录的周边不同方位的8个ML 2.3—2.8爆破事件,截取初至震相前10 s、总时长共60 s的数据(表 3),使用EEMD和小波阈值联合分析方法进行预处理,重构信号与原始信号对比曲线见图 7。
| 表 3 爆破数据统计 Table 3 Blasting statistics |
|
图 7 多个信号处理前后振幅对比曲线 Fig.7 The correlation curve of amplitudes before and after multiple signal processing |
图 7所示,初至震相前10 s及尾波震相到达后一段时间内,原始波形受高频干扰较多,波形震荡摆动,振幅分布范围较大,且数据头尾两段能有效降低高频噪声干扰,突出显示局部主体信号,随机噪声被压制。因此,准确提取信号的时频特征,可有效提高数据精度,为降噪分析提供依据。
4 结论在地震台站数量少且分布稀疏地区,爆破事件记录往往不清晰,特别是对于震级较小的爆破事件,无法在地震波记录中获取有效信息。集合经验模态EEMD方法有效解决了EMD的混频现象,更适用于非平稳、非线性的信号的处理。本文应用EEMD+小波阈值的方法对爆破信号进行预处理,实例表明,借助该方法可有效分离高频、低频信号,爆破信号经IMF分解、重构,信号趋势项被有效去除,噪声得到有效压制。准确分析爆破信息,可为震级、爆破当量计算及爆破精定位等提供服务,为地方行政部门决策提供技术支持。
集合经验模态EEMD和小波阈值结合方法参数设置简单,便于操作,可以广泛应用于其他非线性信号处理,如地震波监测数据、磁电、重力、倾斜等地球物理仪器数据的分析和特征提取。
需要注意的是,采用EEMD方法进行信号分解、重构的标准选取比较主观,容易遗漏信号中的有效成分;小波阈值降噪中小波基的选择对分析结果影响较大,小波基在全局效果可能最佳而对某个区域的效果可能最差。在今后的进一步研究中,将引入神经网络等高级计算方法和熵值作为标准,量化数标,突出局部特征成分,提高数据的准确度。
陈真诚, 吴贤亮, 赵飞骏. EEMD结合小波阈值的光电容积脉搏波信号降噪[J]. 光学精密工程, 2019, 27(6): 1 327-1 334. |
费鸿禄, 刘梦, 曲广建, 等. 基于集合经验模态分解-小波阈值方法的爆破振动信号降噪方法[J]. 爆炸与冲击, 2018, 38(1): 112-118. |
刘莎, 杨建思, 田宝峰, 等. 首都圈地区爆破、矿塌和天然地震的识别研究[J]. 地震学报, 2012, 34(2): 202-213. |
刘洋君, 薛兵, 朱小毅, 等. 地震计自噪声的研究[J]. 地震, 2010, 30(1): 138-146. |
柳建新, 韩世礼, 马捷. 小波分析在地震资料去噪中的应用[J]. 地球物理学进展, 2006, 21(2): 541-545. DOI:10.3969/j.issn.1004-2903.2006.02.032 |
饶运章, 王柳, 饶睿, 等. 基于EMD与小波阈值的爆破震动信号去噪方法[J]. 福州大学学报(自然科学版), 2015, 43(2): 271-277. |
田婕, 张云鹏, 闫鹏, 等. 基于CEEMD的露天深孔爆破振动信号降噪光滑模型[J/OL]. 爆破, (2023-08-14)[2024-05-13].http://kns.cnki.net/kcms/detail/42.1164.TJ.20230814.1056.012.html.
|
王红军, 万鹏. 基于EEMD和小波包变换的早期故障敏感特征获取[J]. 北京理工大学学报, 2013, 33(9): 945-950. DOI:10.3969/j.issn.1001-0645.2013.09.014 |
杨潞霞, 樊东燕, 周任军. 基于EEMD结合二次小波包降噪的齿轮箱故障诊断[J]. 中北大学学报(自然科学版), 2016, 37(3): 262-267. |
张雪英, 谢飞, 乔铁柱, 等. 基于EEMD与改进小波阈值的磁记忆信号降噪研究[J]. 太原理工大学学报, 2015, 46(5): 592-597. |
周红敏, 赵事成, 王慧珍, 等. 基于LMD-MFE-SVD的松动爆破降噪分析[J]. 爆破, 2023, 40(4): 174-182. |
周少辉, 蒋海昆, 曲均浩, 等. 爆破、塌陷识别研究进展综述[J]. 中国地震, 2021, 37(2): 508-522. |
Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition method and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc R Soc Lond A, 1998, 454(1 971): 903-995. |
Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis Method[J]. AADA: Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. |
 2024, Vol. 45
2024, Vol. 45

