2) 中国武汉 430071 地震预警湖北省重点实验室
2) Hubei Key Laboratory of Earthquake Early Warning, Hubei Earthquake Agency, Wuhan 430071, China
地震三要素包括发震时刻、震中和震级,其中震级作为衡量地震大小的尺度,代表地震释放能量的大小。震级新的国家标准(下文简称震级新国标)GB17740—2017《地震震级的规定》(刘瑞丰等,2017)中规定了6种震级的测定方法,其中扩大了测定短周期体波震级mb时振幅的量取范围,并增加了宽频带体波震级mB(BB)的测定要求。
利用实际地震观测资料测定震级,面波震级、地方性震级和体波震级会出现震级饱和现象,而矩震级是一个描述地震绝对大小的力学量,不存在震级饱和问题。因此,震级新国标在发布规则中把矩震级作为对外发布的首选震级,而对于不能及时测定矩震级的地震,从测定震级中“优选”最能反映地震实际情况的结果进行发布(刘瑞丰等, 2018a, b)。
作为国家测震台,湖北麻城地震台(以下简称麻城台)承担着远震分析任务,按照震级新国标要求,在量取最大振幅处测定2个体波震级的过程中发现,震级值与中国地震台网中心的发布震级M有时会相差较大,最大差值甚至大于1级,而单台震级测定的不稳定将直接影响国家地震台网综合震级的测定结果。然而,中国地震台网中心的发布震级M来源并不统一(可能是MS,也可能是MW或者mb)。许多测震台站工作人员为探究本台震级偏差做了诸多分析工作(白伟利等,2020;教聪聪等,2018;李晓东等,2019)。为探究麻城台单台测定体波震级反映地震真实大小的能力,文中选取全球矩心矩张量项目(GCMT)(Dziewonski et al,1981;Ekström etal,2012)中提供的矩震级MW(以下简称矩震级MW),与麻城台测定的2个体波震级进行偏差统计,并就震级大小、震中距、震源深度和方位角作进一步对比,分析单台体波震级的映震能力,为其他测震台站单台地震的分析工作和标准震级的研究提供参考。
1 资料选取根据全球矩心矩张量项目(GCMT)地震目录,选取2018—2019年麻城台记录完整的203个远震事件,计算各地震的体波震级mb和mB(BB)。按照矩震级MW、震中距、震源深度和方位角进行地震分布统计,结果见表 1。
| 表 1 基于震级、震中距、震源深度和方位角的地震事件分布统计 Table 1 Distribution of magnitude, epicentral distance, focal depth, and azimuth of earthquake events |
根据震级新国标GB17740—2017测定短周期体波震级mb,应将垂直向宽频带记录仿真成DD-1短周期地震仪记录,测量P波波列(包括P、pP、sP,甚至可以为PcP及其尾波,一般取在PP波之前)质点运动位移的最大值,计算公式如下
| $ m_b=\lg \left(\frac{A}{T}\right)+Q(\varDelta, h) \quad\left(5^{\circ}<\varDelta<100^{\circ}, T<3 \mathrm{~s}, 0 \leqslant h \leqslant 700 \mathrm{~km}\right) $ | (1) |
新旧mb震级计算公式相同,差别主要在于振幅的量取范围和震中距的测定范围:原mb震级振幅要求在P波到时5 s内量取,周期在0.5—2.5 s(许绍燮等,1999)。
震级新国标规定,测定宽频带体波震级mB(BB)时,应将垂直向速度型宽频带记录上测量P波波列(包括P、pP、sP甚至可以为PcP及其尾波,一般取在PP波之前)质点运动速度的最大值,计算公式如下
| $ m_{\mathrm{B}(\mathrm{BB})}=\lg \left(\frac{V_{\max }}{2 {\rm{ \mathsf{ π}}}}\right)+Q(\varDelta, h) \quad\left(5^{\circ}<\varDelta<100^{\circ}, 0.2 \mathrm{~s}<T<30.0 \mathrm{~s}, 0 \leqslant h \leqslant 700 \mathrm{~km}\right) $ | (2) |
按照GB17740—2017的规定,量取203个远震波形的最大振幅,基于MSDP6.0软件测定体波震级。由于mB(BB)震级需在原始记录上测定,若某地震P波波列原始波形的振幅及周期与背景噪声无明显差异,则不予测定。最终测定得到203个短周期体波震级mb、190个宽频带体波震级mB(BB)。
2.2 震级偏差计算Mi为台站测定的第i个地震震级,M0i为相应地震矩震级MW,Ei为震级偏差,则
| $ E_i=M_i-M_{0 i} $ | (3) |
则平均震级偏差为
| $ \Delta E_i=\frac{1}{N} \sum\nolimits_{i=1}^N\left(M_i-M_{0 i}\right) $ | (4) |
标准差为
| $ \delta_i=\left[\frac{\sum\nolimits_{i=1}^N\left(M_i-M_{0 i}\right)^2}{N-1}\right]^{1 / 2} $ | (5) |
根据式(4)、式(5),计算得到麻城台短周期体波震级mb、宽频带体波震级mB(BB)与矩震级MW的平均偏差分别为-0.233 0、0.207 9,标准差分别为0.479 9、0.414 7。
3 数据分析 3.1 震级偏差分析麻城台体波震级与矩震级偏差计算结果表明:与矩震级MW相比,麻城台单台测定mb震级(以下简称mb震级)平均偏小约0.23,mB(BB)震级(以下简称mB(BB)震级)平均偏大约0.21,mB(BB)震级样本离散程度更低。从平均震级偏差角度来看,mb、mB(BB)震级均具有较强的映震能力且水平相当。
mb、mB(BB)震级偏差分布直方图见图 1,图中横坐标为麻城台体波震级与矩震级MW的差值,即二者的震级偏差,纵坐标为该震级偏差出现的地震频次。

|
图 1 麻城台体波震级mb、mB(BB)与MW震级偏差直方图 Fig.1 Histogram of mb, mB(BB), and MW magnitude deviations at Macheng Seismic Station |
由图 1可见:震级偏差近似呈正态分布;mb震级与矩震级MW的偏差值以负值为主,基本集中在-0.8—0.3范围内,占比85.7%,表明mb震级普遍小于矩震级MW;mB(BB)震级与矩震级MW的偏差值则以正值为主,基本集中在-0.2—0.7范围内,占比86.3%,表明mB(BB)震级较之矩震级MW普遍偏大。这表明mb震级更容易达到饱和状态。通过线性回归分析,得到mb、mB(BB)震级与矩震级MW的关系式。
| $ M_{\mathrm{W}}=0.9523 m_{\mathrm{b}}+0.5033 $ | (6) |
| $ M_{\mathrm{W}}=0.8437 m_{\mathrm{B}(\mathrm{BB})}+0.7552 $ | (7) |
其中相关系数分别为0.807 2、0.868 6,拟合关系见图 2。由以上统计分析结果可知,mB(BB)震级与MW震级的吻合程度更高,因而相较于mb震级有着更强的映震能力。
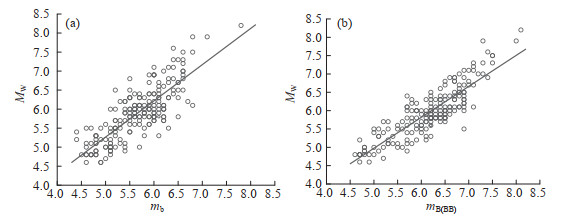
|
图 2 麻城台mb、mB(BB)震级与MW震级回归关系 Fig.2 Regression relationship between mb, mB(BB) magnitudes of Macheng Seismic Station and MW magnitude |
将MW震级按大小分为4个不同区间,计算每个震级区间内麻城台mb、mB(BB)震级与MW震级的平均偏差,计算结果见表 2。由表 2可见,麻城台mb震级与矩震级MW的偏差随震级增大而增大,其中:①MW 4.5—5.9中强地震:平均震级偏差在0.1以内;②MW 6.0—6.9地震:mb震级平均偏小0.37;③7级以上强震:震级偏差平均值接近-0.8(一些地震震级实测偏差甚至大于-1)。而麻城台mB(BB)震级与矩震级MW的偏差分布特征规律不明显,其中MW 5.0—5.9地震震级偏差最大,偏大约0.3,其他震级区间震级偏差均在±0.2以内。
| 表 2 震级偏差与震级关系 Table 2 Relationship between magnitude deviation and magnitude |
综合来看,对于MW 4.5—4.9地震,麻城台测定的mb与mB(BB)震级映震能力相当;对于MW 5.0—5.9地震,mb震级映震能力强于mB(BB)震级;对于MW 6.0以上(尤其是MW 7.0以上)强震,麻城台测定的mb震级易出现震级饱和现象,映震能力较为欠缺。
3.3 震中距与震级偏差之间的关系将震中距分为3个不同区间,分析麻城台mb、mB(BB)震级与MW震级的平均偏差分布特征,统计结果见表 3。由表 3可知,mb、mB(BB)震级与矩震级MW的偏差均随震中距的增加而增大,其中:①9°≤Δ<30°:mb、mB(BB)震级分别比MW震级偏小、偏大约0.1;②Δ≥30°:mb震级比MW震级偏小近0.3,mB(BB)震级比MW震级偏大约0.25。在每个震中距区间内,与mb震级相比,mB(BB)震级与MW震级的偏差相对更小。
| 表 3 震级偏差与震中距关系 Table 3 Relationship between magnitude deviation and epicentral distance |
根据震级新国标中对于浅源、中源及深源地震的定义,把麻城台mb、mB(BB)震级与MW震级平均偏差按震源深度小于60 km、60—300 km及大于300 km进行统计,结果见表 4。由表 4可见:mb、mB(BB)震级与矩震级MW的偏差在3个深度区间均先增大后减小,且偏差值均在±0.3以内,且mB(BB)震级的映震能力略强于mb震级。
| 表 4 震级偏差与震源深度关系 Table 4 Relationship between magnitude deviation and focal depth |
以麻城台位置为坐标原点,将地震事件按4个方位进行划分,分别计算mb、mB(BB)震级与MW震级的偏差平均值,结果见表 5。由表 5可知,对于震中位于麻城台NE向(0°≤α<90°)的地震事件,mb震级与矩震级MW的偏差较大,平均偏小约0.4,而mB(BB)震级与矩震级MW的偏差在0.1以内;位于麻城台SE向(90°≤α<180°)的地震事件,与矩震级MW相比,mb震级平均偏小约0.2,mB(BB)震级平均偏大约0.2;位于麻城台以西(180°≤α<360°)的地震事件,与mB(BB)震级相比,mb震级与矩震级MW的平均偏差较小。分析认为,同一地震台站接收的来自不同方位和区域的地震,受到地震传播射线区域及更广范围内地球内部构造和地球介质非均匀性的影响,地震波能量衰减不一致,导致地震波走时和振幅存在差异性(殷翔等,2012),从而直接影响了单台震级的测定。
| 表 5 震级偏差与方位角关系 Table 5 Relationship between magnitude deviation and azimuth |
综合以上分析,麻城台单台测定的体波震级,mb震级相对易受各种因素影响,震级饱和现象明显,对于6级以上强震及位于台站NE方向地震的映震能力相对欠缺,但与位于台站以西地震的平均震级偏差小于mB(BB)震级;mB(BB)震级受各种因素影响相对较小,与矩震级MW的偏差基本在0.3以内,映震能力相对较强,且测定mB(BB)震级时不需要将地震记录进行仿真,在原始速度型宽频带记录上直接测定即可,便于计算机自动测定。因此,以麻城台单台震级计算结果来看,当需要以体波震级作为发布震级时,优选宽频带体波震级mB(BB)。
4 结论通过对麻城地震台记录的203个远震事件mb、mB(BB)震级与矩震级MW进行震级偏差分析,可以得出以下结论:
(1)mb震级平均偏差约-0.23,mB(BB)震级平均偏差约0.2,mB(BB)震级与MW震级的吻合程度更高。
(2)mb震级相对易受各种因素影响,而mB(BB)震级受各种因素影响相对较小且与矩震级MW偏差基本在0.3以内,映震能力相对较强。以麻城台单台震级测定结果来看,当需要以体波震级作为发布震级时,优选宽频带体波震级mB(BB)。
本次研究震例样本偏少,且多基于统计结果分析,缺少对背后原因的探讨。今后将积累更多震例数据,并结合相关理论对所得结论作进一步验证及讨论。
白伟利, 杨世英, 彭丽娟, 等. 新震级国家标准在大同台的应用与评估[J]. 山西地震, 2020(1): 40-43. |
教聪聪, 钟卫星, 张欢. 佘山台IASPEI新震级与传统震级对比分析[J]. 四川地震, 2018(4): 21-28. |
李晓东, 李姗姗, 张小飞, 等. 库尔勒地震台远震体波震级偏差分析[J]. 地震地磁观测与研究, 2019, 40(2): 34-38. |
刘瑞丰, 陈运泰, 许绍燮, 等. GB17740—2017地震震级的规定[S]. 北京: 中国标准出版社, 2017.
|
刘瑞丰, 陈运泰, 薛峰. 测定的震级之间不应相互换算[J]. 地震地磁观测与研究, 2018a, 39(3): 1-9. |
刘瑞丰, 陈运泰, 薛峰, 等. 如何正确使用新的震级国家标准[J]. 地震地磁观测与研究, 2018b, 39(4): 1-11. |
许绍燮, 陆远忠, 郭履灿, 等. GB17740—1999地震震级的规定[S]. 北京: 中国标准出版社, 1999.
|
殷翔, 徐志国, 任枭, 等. 南京基准地震台与中国地震台网测定体波震级对比分析[J]. 地震地磁观测与研究, 2012, 33(2): 21-26. DOI:10.3969/j.issn.1003-3246.2012.02.004 |
Dziewonski A M, Chou T A, WoodhouseJ H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity[J]. Journal of Geophysical Researoh: Solid Earth, 1981, 86: 2 825-2 852. DOI:10.1029/JB086iB04p02825 |
Ekström G, Nettles M, Dziewoński A M. The global CMT project 2004-2010: Centroid-moment tensors for 13, 017 earthquakes[J]. Physics of the Earth and Planetary Interions, 2012, 200/201: 1-9. DOI:10.1016/j.pepi.2012.04.002 |
 2024, Vol. 45
2024, Vol. 45

