滑坡事件是一种严重的自然灾害,具有突发性和不可预测性等特点,而滑坡体微地震事件可能与滑坡内部岩石破坏、滑坡材料脆性断裂有关,对微地震信号进行检测,可为边坡地下性质分析提供数据基础(Whiteley et al,2019)。
目前,地震自动化检测方法分为传统方法和深度学习类方法。传统方法是指需要人工定义特征函数的方法,比如长短时窗比(STA/LTA)方法(Allen,1978;Baer et al,1987)等。人工设定的特征函数可能不太符合信号特征,在计算过程中精度通常偏低,而且需要进行阈值设定等后续处理,使得传统自动检测方法更多依赖大量人工经验。而深度学习方法基于数据建模方式,依赖于神经网络强大的数据特征构建能力,使得特征函数可以由数据自身进行构建。研究者仅需提供足够的训练数据即可得到良好的精度。比较有代表性的神经算法包括基于卷积神经网络的PhaseNet(Zhu et al,2018)、LPPN(Yu et al,2022)以及基于循环神经网络和Transformer模型的EQTransformer(Mostafa Mousavi et al,2020)、BRNN(Hu et al,2020)。这些方法证明,在地震事件检测中,深度神经网络比传统自动化方法效果更好,但需要海量数据进行训练。例如:用于地震检测的STEAD数据集(Mostafa Mousavi et al,2019)包含25万条人工标注数据,Zhu等(2018)基于此构建了PhaseNet。
深度学习模型具有可从海量数据中自动构建的特征优势,而一个高精度、高鲁棒性的深度学习模型必须经由海量人工标注数据的训练才能保证最终效果。然而,目前模型均是基于天然地震事件进行训练的,岩石边坡微地震事件检测则缺少足够的标注数据用于训练深度学习模型。预训练模型、迁移学习广泛应用于物体检测、自然语言处理工作。例如:RCNN(Girshick et al,2014)模型使用迁移学习方法完成了物体检测工作,而BERT(Devlin et al,2018)、GPT等基于海量数据的预训练模型,经少量微调便可应用于新任务。迁移学习流程可以保证深度学习模型在新的数据上依然具有良好效果。
为解决岩石边坡微地震事件波形标注少的问题,提升深度学习模型在微地震数据上检测的稳定性,设计迁移学习流程来处理微地震检测问题。该流程使用全国范围内人工标注的天然地震数据进行预训练,并使用少量微地震数据进行迁移学习,以减少对人工标注数据的依赖,同时减少训练代价。
1 数据和方法 1.1 训练数据由于岩石边坡微地震数据标注较少,因此在训练过程中使用2种数据:①全国固定地震台网2009—2019年100 Hz采样率人工标注数据,用于模型预训练;②将布设于岩石边坡上台站检测的微地震数据进行人工标注,用于模型迁移学习。神经网络预训练数据分布见图 1。
|
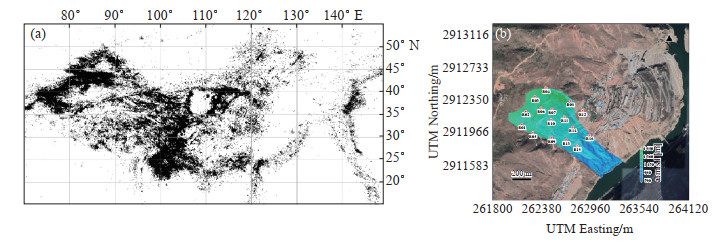
图 1 神经网络预训练数据 (a)地震事件分布;(b)迁移学习数据使用的边坡上地震台分布 Fig.1 The neural network pre-training data |
在预训练过程中,使用Yu等(2023)发布的模型,共包含2 617个台站和103万个天然地震事件(图 1中黑点),每个地震事件波形均包含Pg、Sg震相,且其最大震中距为300 km。而只有16个布设于滑坡体之上的台站提供迁移学习数据,其数据量比预训练数据少得多,事件波形仅包含初至P波。
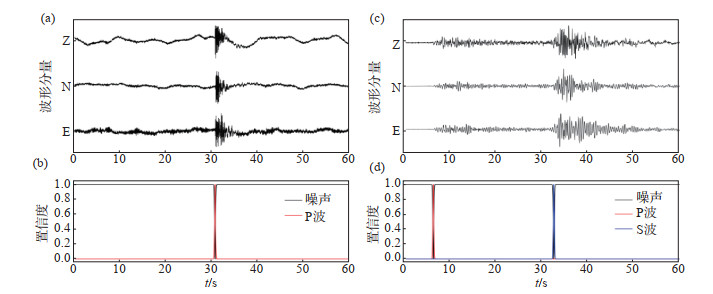
选择一个天然地震波形和微地震波形分别进行人工标注,见图 2,可见2类事件波形有一定区别,其中:微地震事件波形持续时间更短,且主要为P波,而地震事件波形则同时包含P、S波;微地震信号信噪比偏低、频率偏高,可能由微地震能量较小且震中距较近所致。
|
图 2 神经网络训练的微地震数据 (a)微地震波形数据;(b)微地震数据人工标注标签;(c)天然地震波形数据;(d)天然地震标注标签 Fig.2 Microseismic data trained by the neural network |
由于深度神经网络本身包含滤波函数,即卷积网络,因此数据预处理仅指对数据进行去均值和归一化。为训练模型,将人工标注的初至P波放置在固定长度N的任意位置,实际训练中设定N = 6 144,对于三分量100 Hz波形数据,即为61.43 s:
| $ \begin{aligned} x_c^t & =x_c-\mu\left(x_c\right) \\ \hat{x}_c & =\frac{x_c^t}{\max \left(\operatorname{abs}\left(x_c^t\right)\right)+10^{-6}} \end{aligned} $ | (1) |
式中,
将1 050个人工标注样本中的840个样本(占比80%)作为训练集,210个样本作为测试集,对模型进行精度测试。
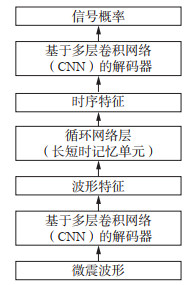
1.2 深度神经网络模型设计为方便迁移学习,使用Yu等(2023)设计的RNN模型作为基础模型。其结构见图 3。如图 3所示,神经网络模型包含编码器、循环网络层、解码器,其中编码器用于处理原始三分量波形数据,其包含多层卷积神经网络,为更好地提取特征,在编码器中加入降采样层,以增强神经网络的感受野,最终将原始数据转换为波形特征;循环网络层由长短时记忆单元构建,其用于处理编码器所得特征并得到时序特征,Yu等(2023)证明,加入循环网络层后神经网络的精度更高;解码器用于处理循环网络层所得时序特征,其中上采样层用于实现点到点的输出,以输出每个P波初动点的概率。最终输出与标签相同,2个特征分别用于表示噪声和P波的概率。
|
图 3 用于微地震检测的深度神经网络结构 Fig.3 Deep neural network structure for microseismic event detection |
在训练过程中使用交叉熵作为损失函数,公式如下
| $ \text { loss }=\frac{1}{N} \sum\nolimits_{j=1}^N \sum\nolimits_{i=1}^2 d_{i, j} \log \left(\frac{1}{p_{i, j}}\right) $ | (2) |
训练分为2个步骤:①基于Yu等(2023)发布的模型,使用天然地震数据进行训练,称为模型A;②使用微地震数据进行迁移学习。在迁移学习过程中,固定迭代20次,批尺寸为32,为验证迁移学习效果,实际上迁移学习中并未使用所有数据进行训练。训练过程中使用Adam优化算法,设定学习率为1×10-3,迭代过程中学习率保持不变。训练后的模型称为模型B。
为方便对比,使用不同迭代次数训练2个模型:使用纯微地震数据迭代20次得到训练模型C,使用纯微地震数据迭代4 000次直至损失函数不再减少,得到训练模型D。模型C代表了与迁移学习相同参数时所能达到的精度,模型D代表了仅用微地震数据训练时所能达到的精度。同理开展后续测试。
2 测试结果 2.1 单个数据测试结果将高信噪比数据(SNR>10)和低信噪比数据(SNR<3)各选2组,对总共4条数据进行模型检测,测试结果见图 4。
|
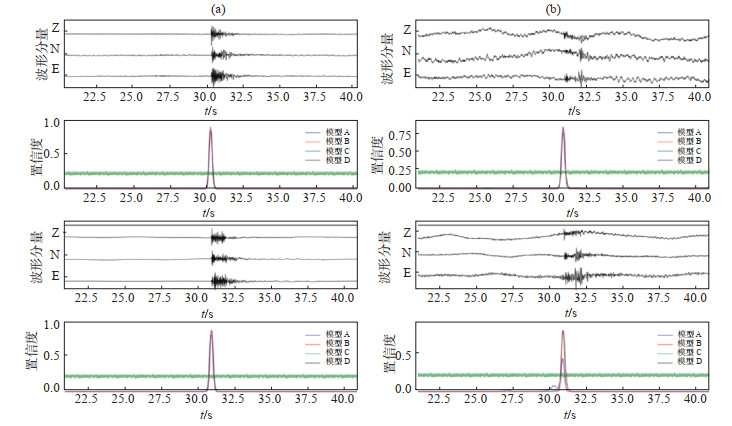
图 4 不同模型检测结果 (a)使用不同模型检测高信噪比波形(SNR>10)置信度;(b)使用不同模型检测低信噪比波形(SNR<3)置信度 Fig.4 Different model detection results |
可以看到,采用模型A进行检测,其精度在低信噪比数据中置信度偏低[图 4(b)],这是因为,模型A仅使用天然地震数据进行训练,对于微地震信号缺少相应的特征学习,导致精度偏低;采用模型C进行检测,由于仅使用微地震数据迭代20次,数据没有收敛,均为噪声波形;采用模型B和模型D进行检测,二者置信度表现相近,意味着使用少量数据迭代20次就可达到预期结果,获得与迭代4 000次的模型D相似的效果。测试表明,迁移学习可以有效减少迭代次数,进而减少对数据的依赖。
2.2 模型精度测试使用原始数据和原始数据加标准差为0.1 s的正态分布噪声,对不同模型进行精度测试。定义人工标注数据与真实数据之间误差小于0.1 s的数据为真阳性样本(True Positive,使用TP表示真阳性样本数量),被检测到但误差大于0.1 s为的数据假阳性样本(False Positive,FP代表数量),人工标注时间与自动拾取时间差大于0.1 s且未被成功检测的为假阴性样本(False Negative,FN)。定义查全率(Recall)为R,R = TP/(TP + FN),表征真实信号中模型能够检测到的比例;查准率(Precision)为P,P = TP/(TP + FP),表征模型检测出的信号中是真实信号的比例;P、R的均值为F1,即F1 = 2PR/(P + R)。在误差统计中,统计真实标注周围误差0.5 s数据的统计均值和标准差。需要说明的是,由于模型C没有收敛,因此选择0.1 s而非Yu等(2023)推荐的0.3 s作为置信度阈值。
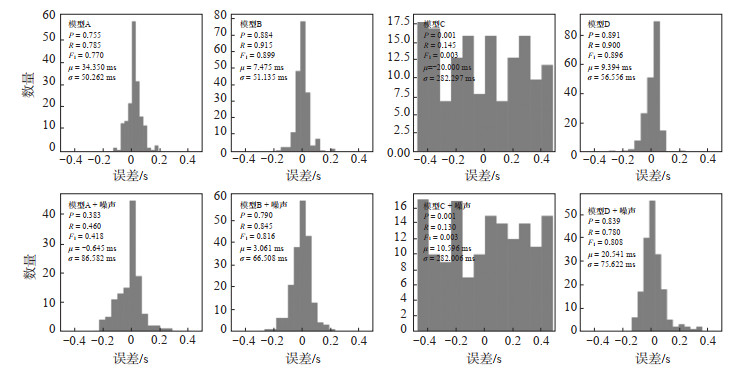
不同深度学习的统计结果见表 1,可知在实际检测中,模型C未收敛而致精度最低;模型A仅使用天然地震数据进行训练,缺少微地震数据样本,F1仅0.77;模型D在训练中迭代4 000次,此时精度较高,意味着模型没有过拟合,可能是由于微地震数据形态比较简单,不容易过拟合;模型B为迁移学习模型,其经少量微地震数据少量迭代即获得最高精度,意味着迁移学习方法不仅可以提升训练效率,还能够提升精度,同时减少数据依赖。绘制不同模型的误差分布,结果见图 5。
| 表 1 不同深度学习模型统计结果 Table 1 Statistical results of different deep learning models |
|
图 5 模型误差分布 (a)原始数据;(b)加噪声数据 Fig.5 Model error distribution |
由图 5可见:①与模型D相比,模型B不仅误差标准差更小,误差均值也更加近0,意味着模型B更适合作为检测模型。②加入噪声数据后,模型A精度下降最多(不考虑C模型),模型D查全率比模型B下降更多,表明模型D在噪声数据中信号检出率降低,而模型B的噪声鲁棒性最佳。
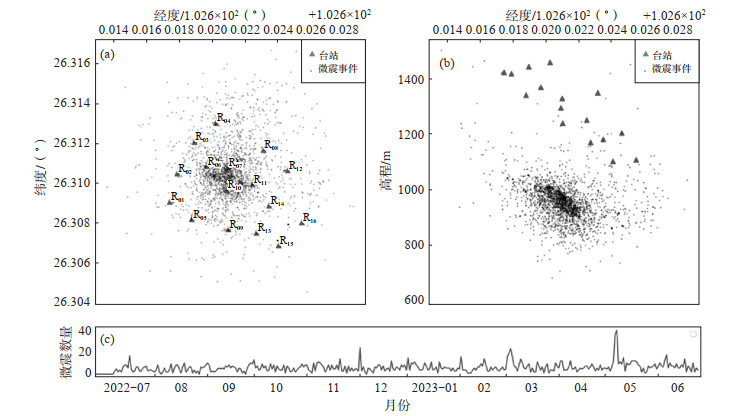
2.3 模型精度测试使用当前模型对边坡区域近1年(2022年7月—2023年6月)的微地震数据进行检测,假设地壳速度结构是均匀的,采用最小二乘法对检测的微地震进行定位,定位效果见图 6。
|
图 6 微地震事件检测效果 (a)微地震事件分布;(b)微地震深度;(c)时间—微震数量图 Fig.6 Microseismic event detection performance |
此处当前检测模型基于单道数据而言,在实际检测过程中,可能由于存在干扰信号而导致在单道数据检测出非微地震信号,因此需要在多个台站同时检测到信号后才能定义为微地震信号。在实际操作中,将2 s时间窗内有6个台站接收信号的事件定义为一个微地震事件。
由图 6可见,在微地震事件检测中,事件分布在R06、R07、R10台站之间呈现一定聚集性[图 6(a)],说明此区域可能存在滑动面。同时,可能受自动检测信号到时精度问题影响,部分到时定位在滑坡区域之外,导致一些微地震事件处在边坡区域外。而在深度分布上,微地震事件则表现出层状聚集性[图 6(b)],可能是潜在的滑坡面。在时间分布上,每日微地震事件数量多在10个以内,未出现异常活跃时段。
3 讨论将迁移学习模型B与使用原始天然地震训练的模型A进行对比,可以看到,模型B的精度可达0.899(以后精度均统一为F1得分,即查全率和查准率的调和均值),而模型A仅为0.770,意味着迁移学习可以有效提升模型在新任务中的精度。同时说明,虽然岩石边坡的微地震事件、天然地震均为震动事件,但是由于物理机制、传播路径等不同,波形具体形态上存在较大差别,因此使用天然地震数据训练的模型无法用于微地震数据。而加入高斯分布噪声后,模型A的精度下降到0.418,模型B的精度下降到0.816,显然模型A受噪声数据影响更大,其数据精度下降程度较大,说明迁移学习方法可以在有效改善模型精度的同时有效增强泛化能力,使得低信噪比数据精度可以更高。
在设计的迁移学习方法中,使用全国固定地震台网数据进行迁移学习,可以有效减小神经网络对数据的依赖。可以看到,仅通过20次训练得到的模型B,使用640条人工标注数据所得精度,与使用840条全量标注数据集训练的模型D精度相当。更加重要的是,模型D的训练经过4 000次迭代,在消耗更多计算资源的同时,会导致模型出现较高的过拟合风险。而未经迁移学习直接迭代20次所得模型C,则由于初始参数问题,模型完全没有收敛。这说明,迁移学习方法在减少数据依赖、减少训练消耗、提升精度等方面均有实践价值。
目前,几乎所有用于震相检测的深度神经网络,如PhaseNet、EQTransformer、LPPN,均是基于人工标注数据集重新进行训练的,但同时所使用的训练数据(三者均使用STEAD数据集训练)又有所欠缺,导致检测模型在中国大陆地区使用时检测精度和查全率较低,即模型不适用于中国大陆地区。这是由数据有偏带来的迁移学习问题。有偏是指,数据仅覆盖某一区域,所训练的模型在其他区域使用时精度降低。预训练模型是基于中国地震台网中心2009—2019年共11年的人工标注数据(目前全球规模最大的地震数据),其未进行信噪比、震相筛选,以尽量保证预训练模型具备较强的泛化能力。所训练模型在2022年泸定MS 6.8地震余震检测(刘泽民等,2023)中取得了良好效果。良好的预训练模型为迁移学习工作提供了基础。
一些文献就数据的区域差异导致的拾取精度问题进行了讨论,如Zhu等(2023)针对每个省设计震相拾取模型,而Yu等(2023)测试表明,模型结构对精度的影响可能比数据分布影响更大。也就是说,在全球范围内,天然地震波形形态存在相似性,不需要进行迁移学习。而岩石边坡微地震信号与天然地震波形在形态上存在较大差别,表明在非天然地震领域,有必要进行迁移学习。这意味着,预训练适用于天然地震向非天然地震信号识别迁移,而非不同地区天然地震之间的迁移。但是目前,针对非天然地震的迁移学习研究较少。
分析发现,迁移学习在数据组织过程中可能存在一些问题,如:数据标注基于单条数据进行,会导致同一个微地震事件波形被不同台站接收,但被分别划分到训练集和测试集。这可能导致实际测试的精度偏高的问题。在未来工作中,应进行更多测试,以确定完成迁移学习训练的标注样本数量。另外,发生微地震事件并不意味着有滑坡发生,而当前所使用的微震检测模型在检测滑坡信号时可能存在一些问题。
4 结束语文中介绍了设计用于岩石边坡微地震信号检测的迁移学习算法流程,该流程使用天然地震数据进行预训练,并且使用少量人工标注的微地震数据进行迁移训练。测试表明,迁移学习可以提升模型的鲁棒性,并可对岩石边坡微地震信号进行有效检测,这为未来滑坡灾害分析提供了基础。基于迁移学习的微地震信号检测模型已进行开源,相应程序可访问 https://gitee.com/cangyeone/seismological-ai-tools获得。
刘泽民, 李俊, 苏金蓉, 等. 2022年四川泸定MS 6.8地震余震序列的自动构建与地震活动性分析[J]. 地球物理学报, 2023, 66(5): 1 976-1 990. |
Allen R V. Automatic earthquake recognition and timing from single traces[J]. Bulletin of the seismological society of America, 1978, 68(5): 1 521-1 532. DOI:10.1785/BSSA0680051521 |
Baer M, Kradolfer U. An automatic phase picker for local and teleseismic events[J]. Bulletin of the Seismological Society of America, 1987, 77(4): 1 437-1 445. DOI:10.1785/BSSA0770041437 |
Devlin J, Chang M W, Lee K, et al. Bert: Pre-training of deep bidirectional transformers for language understanding[C]// Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies Volume 1 C Long and short Papers). Minneapolis, Minnesota: Association for Computational Linguistiscs, 2018.
|
Girshick R, Donahue J, Darrell T, et al. Rich feature hierarchies for accurate object detection and semantic segmentation[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. Columbus, OH, USA: IEEE, 2014: 580-587.
|
Hu J P, Yu Z Y, Kuang W H, et al. Application of machine learning methods in arrival time picking of P waves from reservoir earthquakes[J]. Earthq. Res China, 2020, 34(3): 343-357. |
Mostafa Mousavi S, Sheng Y, Zhu W Q, et al. STanford EArthquake Dataset (STEAD): A global data set of seismic signals for AI[J]. IEEE Access, 2019, 7: 179 464-179 476. DOI:10.1109/ACCESS.2019.2947848 |
Mostafa Mousavi S, Ellsworth W L, Zhu W Q, et al. Earthquake transformer—an attentive deep-learning model for simultaneous earthquake detection and phase picking[J]. Nature communications, 2020, 11(1): 3 952. DOI:10.1038/s41467-020-17591-w |
Whiteley J S, Chambers J E, Uhlemann S, et al. Geophysical monitoring of moisture induced landslides: a review[J]. Reviews of Geophysics, 2019, 57(1): 106-145. DOI:10.1029/2018RG000603 |
Yu Z Y, Wang W T. Lppn: A lightweight network for fast phase picking[J]. Seismological Research Letters, 2022, 93(5): 2 834-2 846. DOI:10.1785/0220210309 |
Yu Z Y, Wang W T, Chen Y N. Benchmark on the accuracy and efficiency of several neural network based phase pickers using datasets from China Seismic Network[J]. Earthquake Science, 2023, 36(2): 113-131. DOI:10.1016/j.eqs.2022.10.001 |
Zhu J, Li Z F, Fang L H. USTC-Pickers: a Unified Set of seismic phase pickers Transfer learned for China[J]. Earthquake Science, 2023, 36(2): 95-112. DOI:10.1016/j.eqs.2023.03.001 |
Zhu W Q, Beroza G C. PhaseNet: A deep-neural-network-based seismic arrival-time picking method[J]. Geophysical Journal International, 2018, 216(1): 261-273. |
 2024, Vol. 45
2024, Vol. 45


