地面上观察到的地震动是震源、地震波传播路径和场地响应的叠加产物。震源处岩石发生破裂所产生的地震波在传播至特定地点过程中会通过复杂场地,而场地条件往往决定了地震动的衰减关系,影响地震波到达后地震动的振幅、频率和持续时间等,对震源参数、震源机制及震级大小的反演和计算至关重要(Aki,1969)。因此,研究地震动衰减关系和地震场地响应,对于工程地震学及理论地震学均具有重要意义。
在地震学中,地震波的衰减效应通常用介质品质因子Q值来度量,Q值也是衡量构造活动性的指标之一。作为介质的重要物理参数,Q值与介质的强度和均匀程度相关:在构造活动稳定地区,地震波的衰减较慢,Q值较大;在构造活动强烈地区,地震波衰减较快,Q值相对较小(陈培善,1985)。因此,通过计算介质品质因子即可知晓研究区域的地震动衰减关系。
场地响应是反映地球介质物理特征的重要参数,是决定地震波传至地面后产生破坏程度的重要因素之一,具体指场地附近理想基岩之上的松软土层对地震波振幅的影响(华卫等,2010;赵翠萍等,2011)。由于实际台站建设条件难以达到理想状态,场地响应不会完全平坦(李祖宁等,2012;段刚等,2017),而这种不平坦的波动趋势恰能反映台站建设的实际场地情况。因此,有必要利用地震事件波形资料计算台站场地响应,为台站建设、地震灾害评估和抗震工程设计提供参考。
1 资料选取将(114.7°—122.5°E,33.8°—40.4°N)范围作为研究区,其覆盖山东整体区域及辽宁、河北、河南、安徽、江苏部分区域。研究区整体为丘陵—平原地貌,地形特征变化不大。为确保“地震事件—地震台站”射线能较好覆盖山东全域,同时确保所选取地震事件记录具备良好的信噪比,对观测台站和地震事件记录选择作如下约定:①地震事件震级ML≥2.0;②每个观测台站至少有3条地震事件记录;③每个地震事件被至少3个所选观测台站记录到。基于上述约定,选取山东地震台网及周边省份地震台网中113个速度型观测台站在2015年至2022年4月记录的329次ML≥2.0地震事件参与场地响应计算。在所选台站中,山东地震台网100个台站,周边省份台网13个台站(图 1,表 1),其中:81个台站配备超宽频带地震计,仪器型号为CMG-3ESP、GL-S60、BBVS-60;32个台站配备短周期地震计,仪器型号主要为FSS-3系列;各台站均配备EDAS-24系列数据采集器。
|
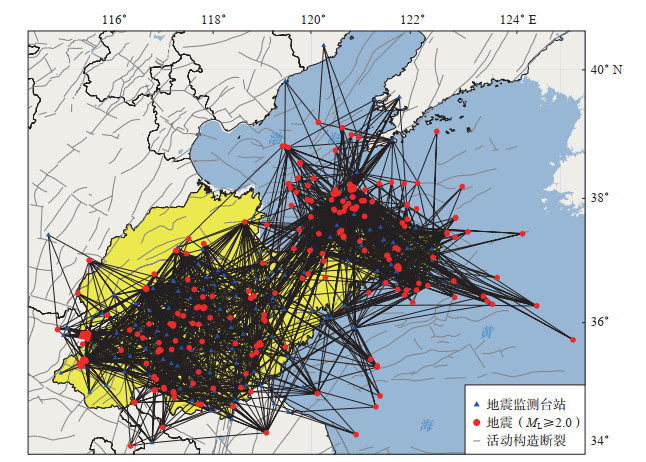
图 1 研究所选台站站址、地震震中分布及地震射线 Fig.1 Epicenters, seismic stations, and seismic ray distribution |
| 表 1 地震台网信息统计 Table 1 Statistics of seismic stations belonging to the seismic network |
所选台站站址、地震震中分布及地震射线见图 1,可见除山东北部较窄区域外,地震事件和监测台站的空间分布较为均匀,射线几乎覆盖整个研究区域,可以满足多台多震联合反演消除地震波辐射花样对地震和台站分布条件的要求(陈继锋等,2010)。
本次研究采用山东地区地震波一维速度模型(表 2),使用SH波资料进行地震波谱资料处理。该速度模型利用山东省数字地震台网2009—2016年地震数据资料,基于Hyposat和HypoDD方法建立,与山东省实际地层发育情况更为吻合(崔鑫等,2017)。
| 表 2 山东地区最优速度模型参数 Table 2 Optimal velocity model parameters in the Shandong area |
对所选取的329个地震事件3 071条地震到时记录,按照从第一个可识别的S震相开始到包含90%的S波能量的原则截取S窗,获得S窗内波形数据(Atkinson et al,1992),采用平移窗谱方法获得稳定观测信号的傅里叶谱。该方法具体操作如下:将S窗内的波形分割成多个小段,每个小段包含256个采样点,相邻小段之间有50%的部分重叠;在每个小段波形的开始和结束处加上5%的COS边瓣,使用快速傅里叶变换计算各小段傅里叶频谱,并进行仪器响应校正和噪声校正,得到“S波窗”内观测信号的位移频谱振幅;此外,从P波到时之前的256个采样点的噪声记录中计算归一化后与信号持时相同的噪声位移频谱振幅,并扣除观测信号中的噪声,得到噪声校正后的位移频谱振幅;对S波的2个水平分量分别进行相同处理,得到其总位移频谱振幅。
2 计算方法和结果 2.1 品质因子Q值第i个地震在第j个台站观测到的地面运动傅里叶谱SH分量振幅描述公式如下
| $ A_{i j}(f)=A_{i 0}(f) \cdot G\left(R_{i j}\right) \cdot S_j(f) \cdot \mathrm{e}^{-\frac{{\rm{ \mathsf{ π}}} f R_{j j}}{Q(f) V}} $ | (1) |
式中,Ai0(f)为第i个地震的震源谱振幅,G(Rij)为几何衰减函数,Rij为震源距,Sj(f)为第j个台站的场地响应项,V为波速,Q(f)为品质因子。
对于S波,G(Rij)满足如下三段几何衰减模型。
| $ G\left(R_{i j}\right)= \begin{cases}R_{i j}^{-b_1} & R_{i j} \leqslant R_1 \\ R_1^{-b_1} \times R_1^{b_2} \times R_{i j}^{-b_2} & R_1<R_{i j} \leqslant R_2 \\ R_1^{-b_1} \times R_1^{b_2} \times R_2^{-b_2} \times R_2^{b_3} \times R_{i j}^{-b_3} & R_{i j}>R_2\end{cases} $ | (2) |
式中:R1和R2分别为震源到三段几何衰减中第一段和第二段转折点的距离(刘丽芳等,2007),其中R1 = 1.5H、R2 = 2.5H,H为莫霍面深度,本研究取H = 33 km(崔鑫等,2017);b1 = 1.0,b2 = 0.0,b3 = 0.5,由不同频率点对应位移振幅与震源距的关系统计所得。
非弹性衰减系数c(f)表达式如下
| $ c(f)=\frac{\log (\mathrm{e}) \cdot {\rm{ \mathsf{ π}}} \cdot f}{Q(f) \cdot V_{\mathrm{S}}} $ | (3) |
其与介质品质因子Q(f)之间的关系为
| $ Q(f)=\frac{\log (\mathrm{e}) \cdot {\rm{ \mathsf{ π}}} \cdot f}{c(f) \cdot V_{\mathrm{S}}} $ | (4) |
将式(1)两边取对数,得到如下关系式
| $ \log A_{i j}(f)=\log A_{i 0}(f)-\log G\left(R_{i j}\right)-c(f) \cdot R_{i j}+\log S_j(f) $ | (5) |
据Atkinson等(1992)的研究,区域品质介质因子Q(f)的计算原理为:首先,假定所有台站的场地响应为1,给定c(f)值,对每个台站记录进行几何扩散和衰减校正处理,得到相应地震的震源谱振幅,同时调整c值大小,使震源谱振幅残差最小;其次,将震源谱振幅平均值设定为某次地震的震源谱,而该台站与该地震的震源谱振幅对数差值平均值即为各台站场地响应对数;最后,考虑各台站场地响应,重新计算各台站校正震源谱振幅,调整c值大小,使同一地震震源谱振幅残差最小(刘杰等,2003)。经过上述步骤的反复迭代反演,即可得到该区域介质非弹性衰减系数c(f)值,进一步得到区域介质品质因子Q(f)(黄玉龙等,2003;兰从欣等,2005)。
反演得到山东地区介质品质因子与频率的关系,公式如下
| $ Q(f)=416.7 f^{0.4728} $ | (6) |
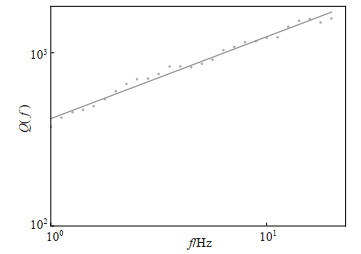
拟合结果见图 2,如图所示,结果拟合较好。
|
图 2 山东地区介质品质因子与频率的关系 Fig.2 Relationship between Q-value and frequency in the Shandong area |
苗庆杰等(2016)选用山东地区46个台站记录的41次ML>2.0地震,得出山东地区Q值随频率f的关系为Q(f)= 457.1f0.4317,与本研究结果相接近,但仍有一定差别。这是因为,虽然其所选区域范围也包括整个山东区域,观测台站和地震事件的分布同样比较均匀,但参与计算的台站数量和符合计算要求的地震事件数量较少,而本研究所选用台站及地震数量更多,震中及地震射线在山东地区覆盖更广,所求解结果更接近于山东地震台网实际。对比可知,本研究所得Q0值相对较高,与山东地区地质构造相对稳定及地震活动性较弱的特征相符。
2.2 场地响应的确定选择Brune(1970)的ω2震源谱模型,假设每个台站在不同地震事件下场地响应均相同,采用Moya方法,运用遗传算法,通过调整震源谱参数,使得不同地震事件得到的同一个台站场地响应的标准差最小(Moya et al,2000)。获得震源谱参数后,将经几何扩散和非弹性衰减校正的位移振幅谱与震源谱进行对比,即可得到每个台站的场地响应(李祖宁等,2012)。
首先对第i个地震在第j个台站观测到的S波傅里叶振幅谱进行几何扩散与衰减的校正:
| $ A_{i j}^{\text {corr }}(f)=A_{i j}(f) \cdot G^{-1}\left(R_{i j}\right) \cdot \mathrm{e}^{\frac{{\rm{ \mathsf{ π}}} f R_{j j}}{Q(f) V_{\mathrm{S}}}} $ | (7) |
通过设定每个地震震源的震源谱参数,即震源谱的低频水平Ω0和拐角频率fc,得到每次地震的理论位移震源谱。在第k个频率点,第i次地震事件对第j个台站的场地响应为
| $ G_{i j}\left(f_k\right) =\frac{A_{i j}^{\mathrm{corr}}\left(f_k\right)}{S_i\left(f_k\right)} $ | (8) |
| $ S_i\left(f_k\right) =\frac{\varOmega_{0 i}}{1+\left(\frac{f_k}{f_{\mathrm{c}}}\right)^2} $ | (9) |
式中,Si(fk)为震源谱。
计算在第k个频率点上第j个台站由不同地震得到的场地响应的平均值和标准偏差,公式如下
| $ \delta_{j k}=\frac{\operatorname{std}\left(S_{i j}\left(f_k\right)\right)}{\operatorname{mean}\left(S_{i j}\left(f_k\right)\right)} $ | (10) |
采用遗传算法,调整每次地震的震源谱参数,使式(11)的值最小,从而迭代计算每次地震的Ω0和fc。公式如下
| $ \operatorname{sum}=\sum\limits_j \sum\limits_k \delta_{j k} $ | (11) |
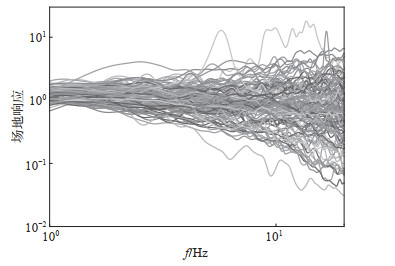
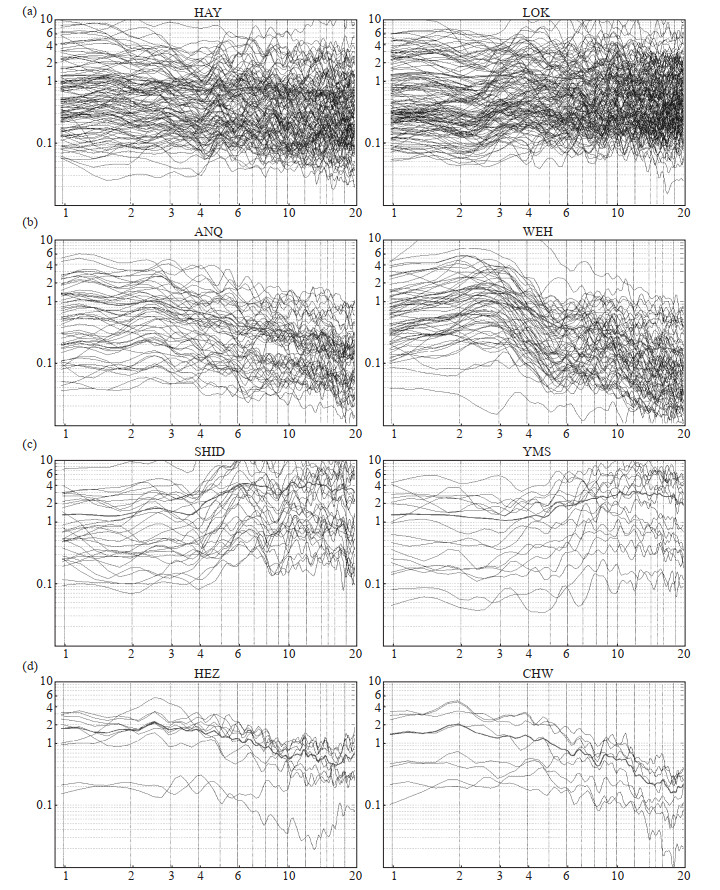
计算得到113个台站的场地响应,结果见图 3。由图可知,这些台站的场地响应在频率域中并不完全平坦,在1—20 Hz的频率范围内,大部分台站的场地响应分布在0.6—2.0,但基本围绕在1.0附近上下波动。结果显示,在113个台站中,有97个台站效果较理想,场地响应具有以下特征:山东地震台网有87个台站场地响应函数无明显放大效应;63个台站的场地响应始终稳定围绕在1.0附近波动,说明该部分台站台基不存在风化层,台站建设选址理想;34个台站的场地响应在低频段围绕在1.0附近波动,且随着频率增大,其中19个台站场地响应衰减,15个台站则出现放大效应,说明这些台站台基存在一定程度的风化层;16个台站的场地响应在低频段出现放大效应,但随着频率增加发生衰减,说明台基可能存在松软沉积层,如成武、曹县、菏泽、东明等台站,即建设在松软沉积层上。受篇幅所限,文中仅列出具有以上显著特征的部分台站场地响应图,见图 4,图中横坐标为频率(Hz),纵坐标为幅值(μm)。
|
图 3 山东及周边区域113个台站的场地响应平均值 Fig.3 Average site response of 113 stations in Shandong and surrounding areas |
|
图 4 8个台站的场地响应迭代反演结果 (a)低频、高频均无明显放大;(b)低频平坦,高频衰减;(c)低频平坦,高频放大;(d)低频放大,高频衰减 Fig.4 Iterative inversion results of site response for 8 stations |
根据圆盘型震源模型,应用震源谱参数,求解中小地震的震源参数。地震矩公式为
| $ M_0=\frac{4 {\rm{ \mathsf{ π}}} \rho V_{\mathrm{S}}^3 \Omega_0}{R_{\theta \phi}} $ | (12) |
式中,ρ为密度,取值为2.7 g/cm3;VS为S波速度,取3.5 km/s;Rθϕ为S波辐射花样系数,对于SH波,取平均值0.66。
震源半径公式为
| $ r=\frac{2.34 V_{\mathrm{S}}}{2 {\rm{ \mathsf{ π}}} f_{\mathrm{c}}} $ | (13) |
应力降公式为
| $ \Delta \sigma=\frac{7 M_0}{16 r^3} $ | (14) |
矩震级公式为
| $ M_{\mathrm{W}}=\frac{2}{3}\left(\lg M_0-9.1\right) $ | (15) |
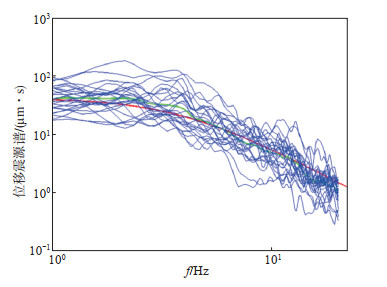
选取山东地区2021—2023年10个ML≥2.5典型震例,利用本研究获得的113个台站的场地响应,重新计算所选震例的震源参数,表 3展示了重新计算后的震源谱参数和震源参数结果。相较之前仅有46个台站的场地响应值,更新后的场地响应的计算结果将使得震中台站的包裹性更好,台站数据更丰富,所得的震源参数结果更加接近于真实情况。以2023年4月8日发生的山东济宁市微山县ML 3.9地震为例,本文给出了该地震的震源谱拟合图,见图 5,图中蓝色线条表示参与计算台站的震源谱结果,绿色线条为由所选台站结果估算出的平均震源谱,红色线条为经过拟合后的震源谱。
| 表 3 部分地震的震源谱参数和震源参数 Table 3 Earthquake source spectra parameters and focus parameters of some earthquakes |
|
图 5 地震震源谱拟合 Fig.5 Earthquake source spectra fitting chart |
选取山东及周边省份地震台网113个速度型观测台站记录的山东地区329个地震波形资料,利用遗传算法,反演得到该区非弹性衰减关系:Q(f) = 416.7 f0.4728,与前人结果相近,但本研究所得结果更接近于区域实际,地震射线在山东地区交叉覆盖更广、更为密集。
场地响应计算结果表明,63个台站的场地响应无明显放大效应,说明其台基良好,与这些台站均处于基岩地基相符;34个台站的场地响应在低频段围绕在1.0附近波动,其中随着频率增大,19个台站场地响应出现衰减,15个台站则出现放大效应,说明这些台基存在一定程度的风化层;16台站的场地响应在低频段出现放大效应,随着频率增加发生明显衰减,说明台基存在一定的松软沉积层。
本研究结果为山东地震监测台网产出更为精确的震源参数等震后产品奠定了数据基础,丰富了数据服务内容,对震级校正、台站场地选择与评价、工程地震和抗震设防评估等具有一定参考意义。
陈继锋, 赵翠萍, 杨立明. 甘肃地区S波非弹性衰减Q值研究[J]. 地震, 2010, 30(1): 125-130. |
陈培善. 地震波的衰减与介质的Q值[J]. 国际地震动态, 1985(4): 1-3, 30. |
崔鑫, 李铂, 朱元清, 等. 基于Hyposat和HypoDD的山东地区地震波一维速度模型[J]. 吉林大学学报(地球科学版), 2017, 47(5): 1 572-1 581. |
段刚, 张丽娜. 福建地区的非弹性衰减和台站场地响应研究[J]. 地球物理学进展, 2017, 32(5): 1 886-1 892. |
华卫, 陈章立, 郑斯华. 利用不同方法估算流动台站的场地响应[J]. 地震, 2010, 30(3): 30-44. |
黄玉龙, 郑斯华, 刘杰, 等. 广东地区地震动衰减和场地响应的研究[J]. 地球物理学报, 2003, 46(1): 54-61. |
兰从欣, 刘杰, 郑斯华, 等. 北京地区中小地震震源参数反演[J]. 地震学报, 2005, 27(5): 498-507. |
李祖宁, 杨贵, 陈光. 福建地区地震波非弹性衰减Q值、场地响应及震源参数研究[J]. 地震研究, 2012, 35(3): 381-386. |
刘杰, 郑斯华, 黄玉龙. 利用遗传算法反演非弹性衰减系数震源参数和场地响应[J]. 地震学报, 2003, 25(2): 211-218. |
刘丽芳, 苏有锦, 刘杰, 等. 用Moya方法反演云南数字地震台站场地响应[J]. 地震研究, 2007, 30(1): 39-42. |
苗庆杰, 刘希强, 石玉燕, 等. 利用遗传算法反演山东地区S波非弹性衰减及场地响应[J]. 震灾防御技术, 2016, 11(4): 800-807. |
赵翠萍, 陈章立, 华卫, 等. 中国大陆主要地震活动区中小地震震源参数研究[J]. 地球物理学报, 2011, 54(6): 1 478-1 489. |
Aki K. Analysis of the seismic coda of local earthquakes as scattered waves[J]. Journal of Geophysical Research, 1969, 74(2): 615-631. DOI:10.1029/JB074i002p00615 |
Atkinson G M, Mereu R F. The shape of ground motion attenuation Curves in Southeastern Canada[J]. Bulletin of the Seismological Society of America, 1992, 82(5): 2 014-2 031. DOI:10.1785/BSSA0820052014 |
Brune J N. Tectonic Stress and the Spectra of Seismic ShearWaves from Earthquakes[J]. Journal of Geophysical Research, 1970, 75(26): 4 997-5 009. DOI:10.1029/JB075i026p04997 |
Moya A, Aguirre J, Irikura K. Inversion of Source Parameters and Site Effects from Strong Ground Motion RecordsUsing Genetic Algorithms[J]. Bulletin of the Seismological Society of America, 2000, 90(4): 977-992. DOI:10.1785/0119990007 |
 2024, Vol. 45
2024, Vol. 45


