0 引言

地磁秒采样观测具有精度高、细节丰富等特点，因此在电磁场、地震预测等研究中得到广泛应用。但也正因为精度高，故常会记录到各种干扰。随着经济的发展，地磁观测台站越来越难以远离人群，这导致车辆干扰、人为活动等影响逐渐增多。其中，车辆干扰是目前秒采样观测中出现频率最多的干扰之一。由于其随机性较强，且持续时间较短，干扰幅度较小（大部分在2 nT以下），因而难以被快速定位，这给台站人员预处理数据带来许多困难。如果不对受车辆干扰的数据进行预处理，又会影响数据质量，尤其是经常受车辆干扰的台站的数据。因此，需要一种方法能快速识别受车辆干扰的数据，以提高数据处理效率，为进一步研究干扰特征提供样本。

小波变换的时间窗、频率窗都可改变。在需要低频信息时采用长时间窗，需要高频信息时采用短时间窗，因此利用小波变换能有效提取信息，且该方法较善于检测信号奇异性（Mallat et al，1992；Tu et al，2005）。目前，小波变换主要用于抑制地磁观测数据的噪声或干扰（吴利辉，2009；谢凡，2011；谢凡等，2011；罗棋等，2019），较少用于提取干扰的研究。因此，本文拟基于小波变换来研究移动车辆干扰自动识别处理方法。设计了一种自动识别处理移动车辆干扰的方法，即利用小波变换检索移动车辆干扰，并根据干扰曲线斜率绝对值较大的特点判断干扰发生的起止时间；再通过多台对比排除磁场扰动所造成的误判，得到移动车辆干扰的发生时间；最后进行预处理。使用多种常见的小波基函数对样本数据进行计算，统计分析出适用于识别提取移动车辆干扰的小波基函数。

1 方法与原理

移动车辆干扰自动识别与处理方法包括以下步骤：①对含移动车辆干扰的秒采样数据进行小波分解；②利用小波分解的高频结果，判断干扰发生的时间；③将受干扰台的计算结果与参考台进行对比，将共同识别出的异常认作磁场扰动，以此排除磁扰的影响，确定移动车辆干扰；④对移动车辆干扰识别结果进行自动处理。

1.1 小波变换

小波变换采用Mallat算法，其过程为：运用低通、高通分解滤波器H、G将信号逐层分解，再运用低通、高通重构滤波器h、g逐层重构信号，其中，H、h对应尺度函数；G、g对应小波函数。分解公式为

$ A_j[f(t)]=\sum H(2 t-k) A_{j-1}[f(t)] $

(1)

$ D_j[f(t)]=\sum_k G(2 t-k) A_{j-1}[f(t)] $

(2)

式中，f(t)为待分解信号；j为分解尺度；A_j[f(t)]表示尺度上j的近似系数；D_j[f(t)]表示尺度j上的细节系数。重构公式为

$ A_j[f(t)]=2\left\{\sum_k h(t-2 k) A_{j-1}[f(t)]+\sum_k g(t-2 k) D_{j+1}[f(t)]\right\} $

(3)

1.2 提取受干扰的异常数据

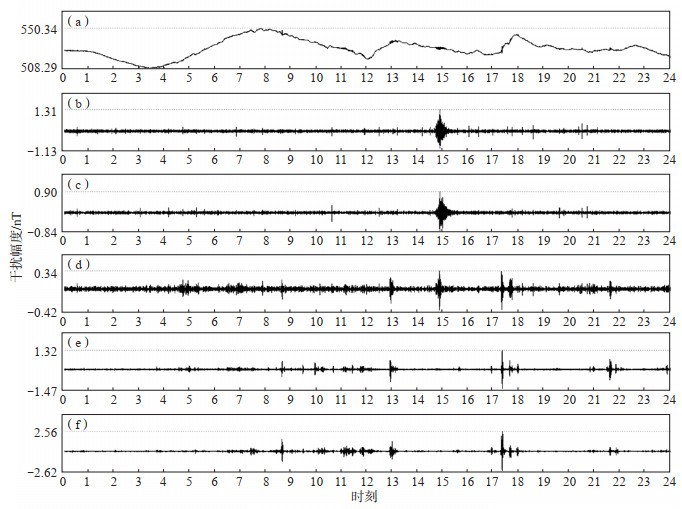
对数据进行小波分解后发现，移动车辆干扰、噪声等信息集中在高频部分，且不同频率的干扰信息会出现在不同尺度变换后的高频成分中。通过对比发现，尺度为1或2时，提取的数据信息主要是噪声、地震等高频信息；尺度为3时，会提取出频率较高的干扰数据信息；尺度为5或6时，磁扰信息会较丰富；尺度为7及以上时，提取的高频数据信息较少；当尺度为4时，提取的数据则包含较多的移动车辆干扰信息。因此，以2022年3月16日巴彦淖尔地震台FHDZ-M15观测系统地磁水平分量H数据为例，选择尺度4进行小波分解（图 1）。

为从小波分解的高频成分中提取移动车辆干扰信息，采用阈值判断的方法：首先，计算样本数据的均值和标准差；然后，选择合适的倍数，以该倍数乘以标准差再加减均值作为上下限阈值，若信号值大于上限阈值或小于下限阈值时，就认为此信号异常。但是，因为小波分解后得到的是重构信号，异常时间段相比实际发生的干扰时间段存在偏移，所以干扰的起止时间难以直接根据小波的异常值来确定，因此利用小波变换检索到干扰后，还需采用其他方法以获得干扰的起止时间。本文中，利用移动车辆干扰曲线形态特征来确定干扰的起止时间。相较于正常背景曲线，移动车辆干扰曲线在短时间内迅速上升和下降，即曲线斜率的绝对值比正常背景曲线高。据此，采用的方法为：考虑到一般移动车辆干扰持续时间不超过60 s，即在小波异常高值前后共120 s内，故计算数据的一阶导数即斜率；通过阈值筛选出比正常背景值高的斜率绝对值，反推出其对应的原始数据位置，以此确定干扰发生的时间段，其中，为适应数据局部变化，阈值根据这120 s内数据一阶导数的均值和标准差来确定。移动车辆产生干扰时，往往多个测项分量同时受到影响。为了提高识别率，对磁偏角D、水平分量H、磁偏角Z分别进行上述操作，以其中持续时间最长的作为最终干扰时间段结果。

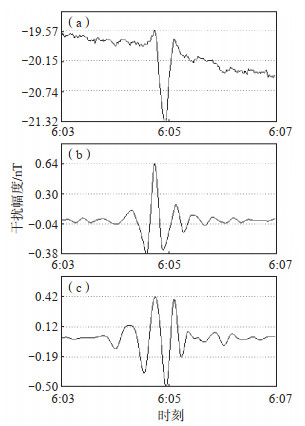
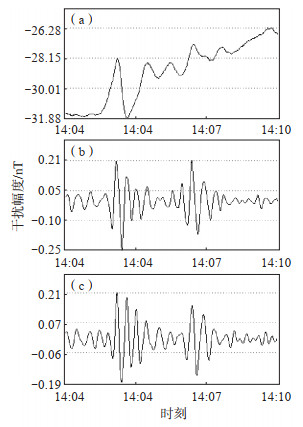
1.3 识别受移动车辆干扰的数据

由上述方法识别出的干扰，除了移动车辆干扰外，还包含磁场扰动变化，这2类干扰的形态具有相似性，发生频率在一定范围内重合（图 2、3）。但是，磁扰与移动车辆干扰的最大区别为：磁扰发生在大范围区域内，能被多个台站记录到；而移动车辆干扰仅在单台发生。因此，通过多台对比方法来加以区分，即选择受干扰台附近的台站为参考台，分别利用小波分解提取干扰时间，若受干扰台与参考台在同一时间都检测出干扰，则此干扰为磁扰；反之，则为移动车辆干扰。为防止当仅用1个参考台作对比时参考台与受干扰台恰同时存在干扰的情况出现，因此选择2个参考台，进行3个台对比，以剔除磁扰的影响。

1.4 移动车辆干扰数据预处理

采用线性插值法、相关差值拟合法对移动车辆干扰进行预处理，并对预处理效果进行比较。

（1）线性插值法。移动车辆干扰持续时间较短时，可根据干扰前后的正常背景记录值x₁、x₂，以及受干扰影响的数据个数n，得到干扰期间的第i个记录值x_i为

$ x_i=x_1+i \cdot \frac{x_2-x_1}{n+1} $

(4)

（2）相关差值拟合法。相邻台站的地磁记录具有较高相关性，2个台站间数据的差值往往在1个固定值附近浮动，因此可根据数据相对差值和参考台数据来模拟受干扰台数据。由于不同台站观测场地不同，这些台站的观测数据对太阳活动等的反映程度也会存在差异，因此不适宜用全天数据的差值来进行拟合。故首先计算移动车辆干扰前后各1 min内受干扰台和参考台的相对差值，求其平均值，再加上参考台的记录值，将其作为受干扰台的预处理数据。

2 计算结果分析 2.1 样本数据简介

选择受移动车辆干扰较频繁的溧阳地震台、河池地震台2022年磁通门磁力仪观测数据作为样本。这2个台磁通门磁力仪附近建有公路，磁力仪常记录到来往车辆对观测数据造成的干扰。挑选104个典型移动车辆干扰事件进行分析，并以高邮地震台、南京地震台作为溧阳地震台的参考台，乌鲁木齐地震台、喀什栏杆乡地震台作为河池地震台的参考台。

根据人工判别的结果，溧阳地震台、河池地震台地磁观测数据受车辆干扰的幅度大多为0.2—5.0 nT，持续时间小于1 min。磁偏角D、水平分量H受车辆干扰更明显，垂直分量Z受车辆干扰较少。

2.2 干扰数据识别效果分析

计算分析中使用的小波基函数包括：dbN小波系中的db2—db10小波、coifN小波系中的coif1—coif5小波及symN小波系中的sym2—sym8小波。经过试验发现，是否去除噪声对识别效果影响较小，因此直接对原始数据进行小波分解。对于车辆干扰以外的其他干扰，如上文所述，可以通过尺度的选择来尽可能排除，对于不易排除的磁扰，可通过多台对比来去除。

计算中阈值的选择较关键。若阈值偏小，会误识别出相对剧烈的正常背景变化；若阈值偏大，会遗漏幅度较小的移动车辆干扰。在进行大量尝试后，为不同测项分量、不同小波基函数选择了不同的阈值，以尽可能在保证识别正确率的情况下筛选出最多的车辆干扰。溧阳地震台磁D、H分量的阈值为2.3—5.0，Z分量的为5—6；河池地震台磁D、H分量的阈值为1—2，Z分量的为2.5—3.5。

按上述方法对样本数据进行计算，将得到的结果与人工判别结果进行对比，统计了21种小波基函数的移动车辆干扰识别率（识别结果中的移动车辆干扰数/人工判别的移动车辆干扰数）和识别正确率（识别结果中的移动车辆干扰数/识别结果总数）（表 1），表 1中按干扰识别率从高到低进行排序。

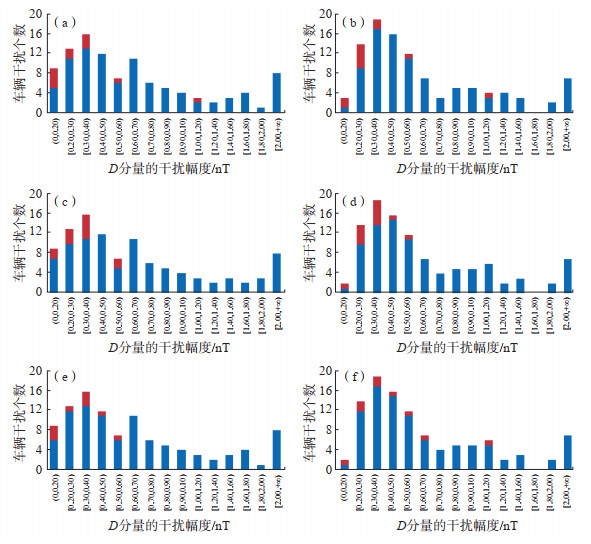
由表 1可见，大部分小波的移动车辆干扰识别率大于80%。sym8小波的识别率最高，大于90%；其次为db6小波，识别率达89%。不能识别出的移动车辆干扰主要包括以下几种情况：①大部分干扰幅度较小，不足0.4 nT，以识别能力较强的db6、db9、sym8小波为例（图 4），未识别出的移动车辆干扰幅度主要为0.1—0.4 nT，若选择较小的阈值，则可以减少未识别的数量；②停驻车辆造成的干扰形态表现为台阶，大于0.4 nT的未识别车辆干扰大多数为停驻车辆干扰；③发生磁场扰动的同时，存在移动车辆干扰，导致这些干扰连同磁扰一起被排除，这是干扰幅度大于0.4 nT的移动车辆干扰未能被识别的原因之一；④受干扰台发生移动车辆干扰时，参考台恰好也存在干扰，这导致其被误判为磁扰而被排除，此种情况较少，实际运用时若选择的参考台数据质量不佳、曲线不正常变化较多时，就会对识别结果造成影响。

从识别结果的正确率来看，db9小波的正确率最高，为83%；db6、db5小波的均大于80%；其他大部分小波的为70%—80%。影响正确率的主要因素是，一些干扰幅度为0.2—0.5 nT的短时间正常变化或磁扰被误识别为车辆干扰。导致其发生的原因有以下几点：①正常背景值变化、磁扰的幅度与台站场地环境有关，如果在短时间内受干扰台场地环境变化相对较大，但参考台变化较小，或2个参考台之一变化较小，小波分解没有同时出现高值，就会造成误判，这一点在磁静日时更明显；②人为活动（携带铁磁性物质）干扰会导致误判，其形态与移动车辆干扰存在一定相似性，当阈值设置较低、人为活动干扰幅度较大时，会造成误判。

移动车辆干扰的识别率和正确率之间存在一定矛盾：如果降低阈值，可以识别出更多小幅度干扰，但同时可能会造成更多误判，降低了正确率；如果提高阈值，可以提高识别正确率，但一些小幅度的移动车辆干扰会被遗漏，降低了识别率。因此需要把握识别率和正确率之间的平衡。另外，参考台的选择也很重要，选取数据质量较好的参考台可以得到较好的识别结果，有效提高识别率和正确率。

需要注意的是，因受干扰台与参考台场地特性不同、细微变化不完全一致，人工判别有时很难区分小幅度的车辆干扰和正常变化，尤其当正常变化较大时，对于小幅度（小于0.4 nT）的移动车辆干扰，不能保证人工判别完全正确。况且，幅度大的移动车辆干扰对数据质量的影响更大，因此，识别处理幅度较大的移动车辆干扰更有实用意义。

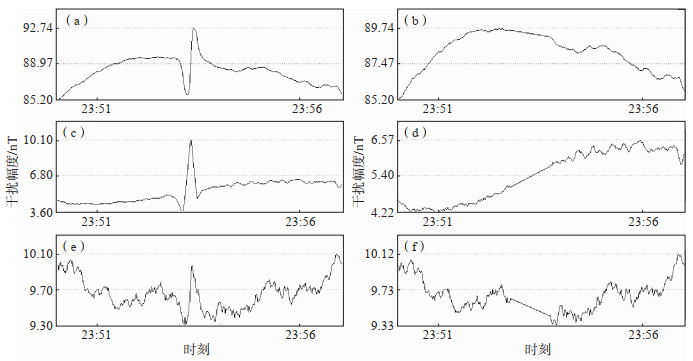
2.3 干扰数据预处理分析

线性插值法预处理效果如图 5所示。其优势：使用单台数据即可计算，当参考台数据质量不佳或存在严重干扰时，对移动车辆干扰进行预处理仍然能得到较好效果。不足：因曲线呈直线，当背景曲线本身存在扰动时，预处理效果较差。因此，该方法仅适用于磁场较平静的时段，或无合适参考台时使用。

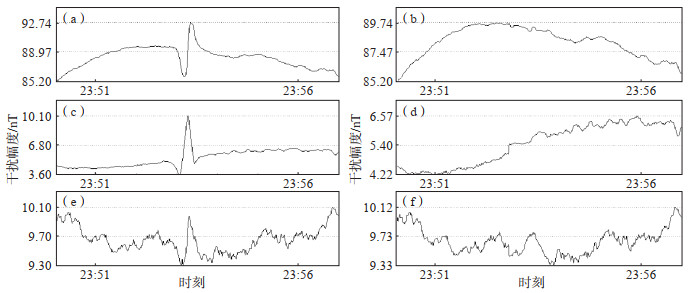
相关差值拟合法效果如图 6所示。其优势：当选择合适的参考台时，预处理后数据更贴近磁场曲线变化，能得到较好的预处理效果。不足：依赖参考台的数据质量及受干扰台与参考台间的相关性。当参考台受到严重干扰时，或当局部时段受干扰台与参考台背景值曲线间相关性不强时，预处理结果可能与该台真实磁场变化间存在差异。总体而言，大多数情况下，相关差值拟合法的预处理效果更好，适用性更强。

3 应用效果检验

按照上述移动车辆干扰识别和预处理方法，使用识别能力较好的sym8、db6、db9小波，从2022年河池地震台磁通门磁力仪观测数据中选择一段样本以外的原始数据进行计算，以检测应用效果。将识别结果与人工判别结果进行比较（表 2），此段数据中共有61次移动车辆干扰，3种小波的干扰识别率均大于95%；db6、db9小波的识别正确率较高，均大于92%，sym8小波相对低一些，为87.88%。总体而言，应用效果较好。

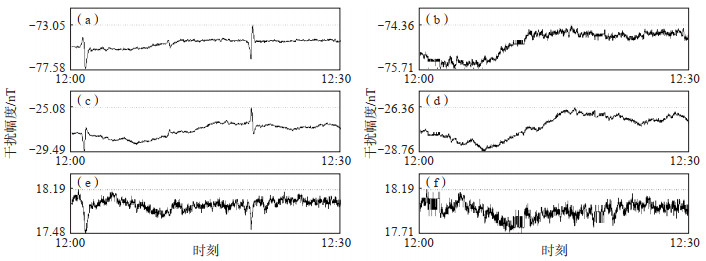
此次应用检验中干扰识别率、正确率较高的主要原因是河池地震台测值受到的移动车辆干扰幅度较大，在选取的数据中，超过30%的数据干扰幅度大于1.0 nT，超过37%的干扰幅度为0.5—1.0 nT。而研究时选择的样本以溧阳地震台的数据为主，干扰幅度小于0.5 nT的小幅度干扰较多，超过40%。这也说明该方法对于干扰幅度大于0.5 nT的移动车辆干扰识别更有效。图 7为进行应用检验的原始数据曲线和经过自动干扰识别、预处理后的数据曲线示例。

4 结论

基于小波变换，设计了移动车辆干扰自动识别处理方法：①对秒采样数据进行小波分解；②以小波分解后的高频结果为基础提取异常值，利用干扰曲线的斜率绝对值大于正常背景曲线斜率的特点，判断干扰发生的起止时间；③将干扰台的计算结果与参考台进行对比，将共同识别出的异常认作磁场扰动，将其排除，确定移动车辆干扰；④对移动车辆干扰识别结果进行自动处理。采用上述方法，通过对常见的21种小波基函数进行计算和分析认为，db6、db9、sym8小波识别移动车辆干扰效果较好。

此方法还存在一些不足：使用的阈值参数较多，为达到较好的识别效果，需要反复尝试寻找合适的阈值；阶变形态的驻停车辆干扰不能较好地被识别；小幅度的移动车辆干扰不能完全被识别等。后续将进一步研究更加完善的干扰自动识别预处理方法。

感谢中国地震局地球物理研究所国家地磁台网中心提供地磁数据，感谢审稿专家提出修改意见和建议。