0 引言

小泉沟地震台位于焉耆县七个星镇以西，地处库尔勒断裂与兴地断裂之间（图 1），2014年建成，2015年投入使用，是半地下室结构的地面台站，摆房位于地面以下2.5 m，摆墩基岩完整，岩性为花岗岩（段绍鑫等，2019）。2018年4月之前使用CTS-1EF型地震计，数据采集器为EDAS-24IP型。2018年4月至今使用CMG-3ESPC-120型地震计，数据采集器为EDAS-24GN型。2019年1—3月地震计出现故障，4月2日更换为CMG-3ESPC-120型地震计。小泉沟地震台观测数据通过光纤传输，稳定可靠。小泉沟地震台地震观测仪器参数见表 1。

1 计算功率谱密度PSD

由于风、海浪、交通运行、人为活动等各种原因，地球表面存在着微小的震动，它们可对地震观测产生干扰并影响观测结果，通常称其为环境背景噪声。环境背景噪声限制了地震台站观测能力的提高，即使采用较灵敏的观测仪器，也不能清晰地记录到小于台站背景噪声的微小信号，因此地震观测台站的背景噪声及其随频率的分布对于地震观测非常重要（何彦等，2006；许可等，2015；杨龙翔等，2015；侯颉等，2019）。

Welch算法是对周期图法的一种改进，它包括对信号重叠分段、加窗处理，求出各段功率谱后再求平均功率谱，具有直观及便于理解、计算等优点。设时间函数f(t)为地震记录中的位移，应用傅里叶变换（任枭等，2004），将其转换为功率谱F(ω)，则f(t)与功率谱F(ω)之间的关系如下

$ \int_{-\infty}^{+\infty}|f(t)|^2 \mathrm{~d} t=\frac{1}{{\rm{ \mathsf{ π}}}} \int_0^{\infty}|F(\omega)|^2 \mathrm{~d} \omega $

(1)

$ F(\omega)=\int_{-\infty}^{+\infty} f(t) \mathrm{e}^{-i \omega t} \mathrm{~d} t $

(2)

根据台站实际仪器种类及零极点、增益参数，使用童汪练老师研制开发的软件，计算数字地震仪的地动噪声功率谱密度。

选取2020年4月5日0—4时连续5 h的小泉沟地震台波形数据计算台基背景噪声功率谱密度，所选数据没有地震记录和明显的干扰。计算得到小泉沟地震台UD向1/3倍频程带宽1—20 Hz各段的平均地动噪声RMS值为2.88×10^-9 m/s，远小于3.16×10^-8 m/s，由此可见，小泉沟地震台台基较好，符合Ⅰ类台基标准。

2 计算概率密度函数PDF

1993年Peterson定量分析了全球各地75个固定地震台站的地震噪声功率谱密度，得到了包括新高噪声模型（NHNM）和新低噪声模型（NLNM）的全球地震背景噪声模型，并将其应用于地震台站环境噪声水平评价。2004年McNamara和Buland发展了Peterson的地球噪声模型估算法，通过计算大量功率谱密度曲线的概率函数（PDF）分布，得到台站噪声水平最大概率分布模型和台网噪声最低概率模型（谢江涛等，2018；邓明文等, 2021a, 2021b）。PDF统计方法可以对各种扰动进行统一处理，以避免噪声记录的人为因素影响，能全面反映台站噪声水平的动态变化。功率谱概率密度函数法在计算过程中不需要排除包括地震在内的突发事件，而是对所有记录数据进行处理；在保持数据连续性的同时，背景噪声的影响也体现在概率密度函数PDF的概率值中（杨千里等，2019）。通过概率密度函数可以得到某个时间域上某个功率值的发生概率，该概率值可直接反映噪声的时间变化特征。

为了对功率谱密度进行充分采样，按1/8倍频程间隔计算整个周期范围内各中心频率的平均值（谢江涛等，2018）。功率谱密度值在短周期（高频率）T_s与长周期（低频率）T_l = 2T_s之间进行平均，对应的中心周期T_c为倍频程内的几何平均值

$ T_{\mathrm{c}}=\sqrt{T_{\mathrm{s}} \times T_1} $

(3)

T_s以1/8倍频程增加用于计算下一个间隔的功率谱密度平均值T_s = T_s×2^0.125。重新计算T_l、T_s值，并计算下一个中心周期T_c在T_l和T_s周期范围内的功率谱密度平均值。

对于每一个给定的中心周期T_c，概率密度函数表示为

$ P\left(T_{\mathrm{c}}\right)=\frac{N_{P_{T_{\mathrm{c}}}}}{N_{T_{\mathrm{c}}}} $

(4)

其中，N_PTc为功率谱密度值落在某个1dB间隔范围内的数量；P的范围为-200——-40 dB；N_Tc为中心周期T_c在功率谱密度值范围内估计值总数。

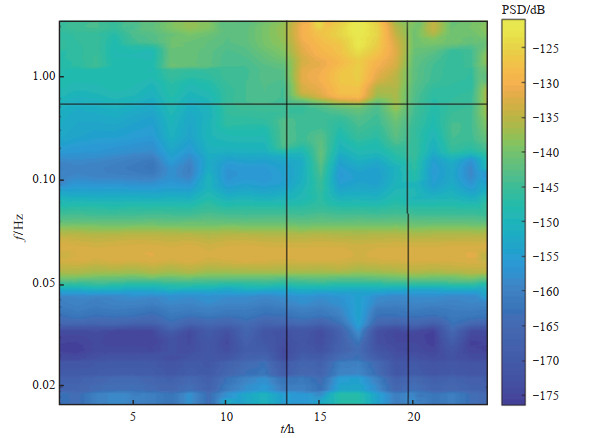
首先，对2020年4月5日全天24 h的小泉沟地震台波形数据进行计算，得到台基背景噪声日变化（图 2）。由图 2可见，高频部分在12—20时背景噪声明显高于其他时间段，基本大于-135 dB；在夜间背景噪声明显降低，基本小于-145 dB，其中，0—5时背景噪声最小，这种日变现象符合人类日间活动的规律。

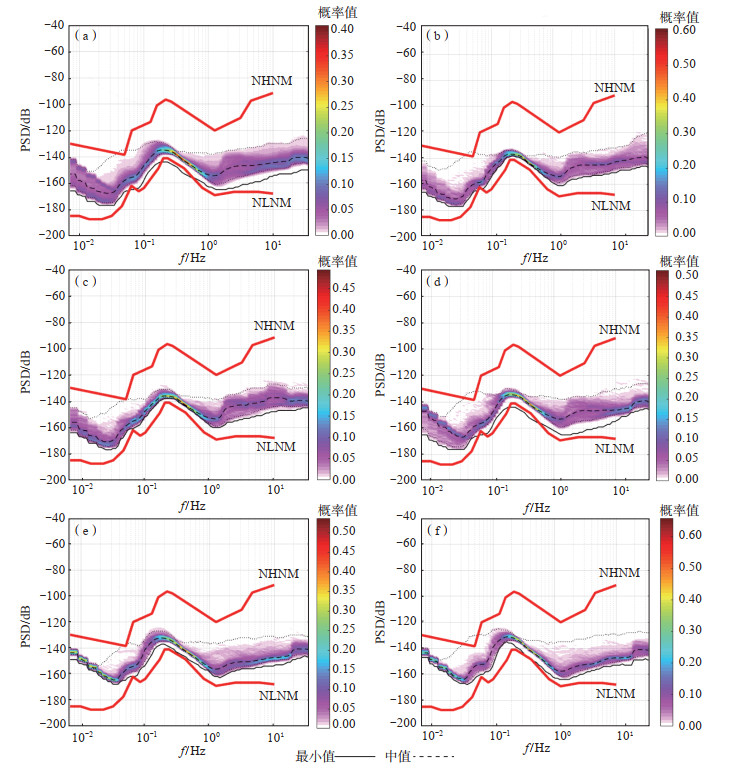
背景噪声长周期部分主要受自然环境因素影响，如温度、气压的变化会引起长周期噪声的提高。对2019年4月至2020年3月小泉沟地震台连续波形数据进行计算，得到小泉沟地震台台基背景噪声年变化（图 3）。由图 3可见，背景噪声整体水平较低，低于NHNM与NLNM的平均值；2019年5月、8月长周期背景噪声较低，PSD曲线主要集中在-160 dB以下；11月长周期背景噪声开始升高；12月和2020年1月PSD曲线分布较集中，背景噪声由之前的-160 dB上升到-140 dB左右。因此，小泉沟地震台背景噪声年变化特征为夏季背景噪声最低，随着天气变冷、昼夜温差变大，背景噪声慢慢升高，到冬季12月、次年1月背景噪声达到最高。

3 结论

通过对小泉沟地震台12个月的连续波形数据进行功率谱密度、概率密度函数计算得到以下结论。

（1）小泉沟地震台台基较好，台基背景噪声较低，属于Ⅰ类台基。

（2）小泉沟地震台背景噪声日变化特征符合人类日间活动的规律，受人为活动影响较大，高频部分在12—20时背景噪声明显增大，基本上大于-135 dB；在夜间背景噪声明显降低，0—5时背景噪声最低。

（3）小泉沟地震台背景噪声年变化受气温、气压的影响较大，表现为夏季背景噪声最低，受天气变冷、昼夜温差变大、刮风的影响背景噪声逐渐升高，在12月、次年1月背景噪声达到最高。

为了能够得到干扰更小、观测质量更高的观测数据，结合以上结论可以在后续工作中对观测环境进行相关改造，如在观测站点附近增加警示牌来减少人为活动的影响，通过观测室加装保温门、下人口加装保温盖、地震计加装保温罩来减小气温、气压的影响。