1 研究背景

地下水不仅可以直接反映含水层地下水流的流量，还可以反映由于受力状态改变引起的孔隙压力变化。井水位潮汐受到固体潮、气压潮等多种荷载的影响，观测井可以准确的记录潮汐波动，其中M₂波由月球引起且受气压影响的程度较小，不受气温和气压的影响，因此M₂波是水位固体潮分析中最有效的潮汐波分量。观测数据进行潮汐分析时，选取不同的时间窗长会影响潮汐因子的计算精度。Doan（2006）指出，为提取半日潮和日潮，最小持续时间为2天，为区分日潮和半日潮2个主要子带的分离至少需要15天。陈莹（2012）选取数据采样长度不同的数据提取M₂波幅度，得出了以1个月为尺度求出的M₂波振幅最佳，适合作为采样数据的时间长度。选取合适的时间窗长对计算潮汐因子精度至关重要。

作者发现，在一些文章中计算M₂波潮汐因子时选取的时间窗长过短，故分析时间窗长选取对潮汐因子的影响。本文以鲁07栖霞井为研究对象，利用Baytap-G程序计算M₂波潮汐因子相对误差，分析选择不同时间窗长对潮汐因子的误差影响，从而论证选取的最佳时间窗长。

2 研究方法及研究结果

Baytap-G程序是以贝叶斯原理为基础开发的一款固体潮分析程序，可以用来求潮汐因子及潮汐因子滞后的值。Baytap-G程序的优点在于能够自动剔除异常数据和井水位的脉冲变化和阶梯变化，并且能够自动提取潮汐变化项，求出潮汐因子和潮汐因子误差。

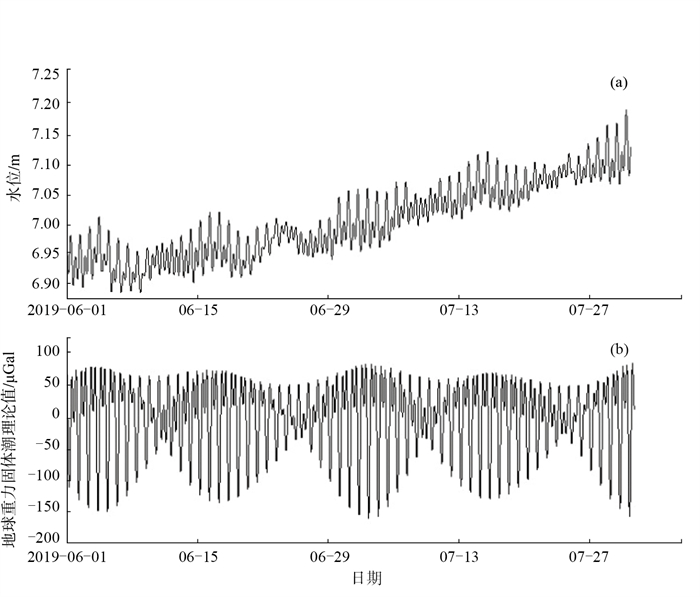
选取2019年6月和7月井水位观测数据，从水位数据曲线形态看，水位变化相对平稳，且有明显的日变周期和月变周期。从水位变化和固体潮变化的对比，可以看出井水位对固体潮的响应比较明显，说明鲁07栖霞井水位对地壳应力应变有灵敏的反应，并且存在长趋势项。

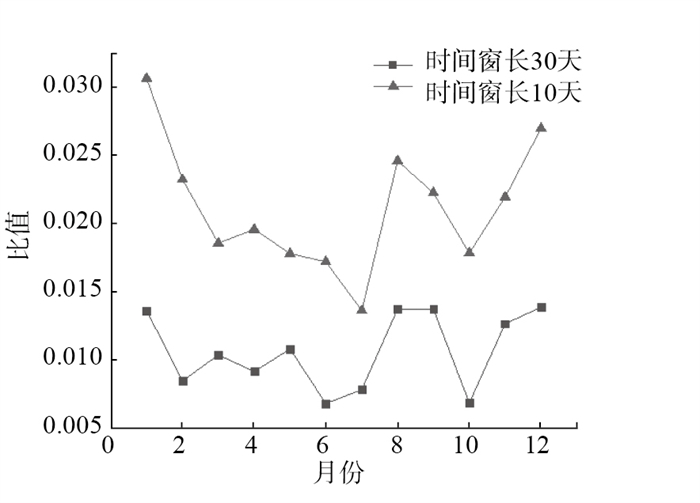
用Baytap-G程序计算鲁07井2019年水位数据，分别设置时间窗长为30天，步长为5天和时间窗长为10天，步长为5天计算M₂波的潮汐因子相对误差，将每个月相对误差平均值绘制折线图，如图 2所示。从图 2中可以看出，潮汐因子相对误差不断变化，但窗长选取为10天的误差明显大于窗长选取为30天的误差。潮汐因子相对误差在一年中有些月份误差比较大，符合观测井背景资料中给出的井水位受季节性农田灌溉条件的影响。因此在进行数据分析时，人为因素造成的影响也需考虑进来。

3 结论与讨论

通过对M₂波不同时间窗长的潮汐因子误差进行分析，可以看出，如果时间窗口选择时间过短，会产生较大的潮汐因子误差，而数据时间过长，则叠加更多干扰。时长一个月的数据经历了完整的大小潮周期，可以使数据计算结果更加准确。此外，在数据分析过程中，人为因素对数据的影响需予以考虑。