1 研究背景

信息预测理论是翁文波院士在20世纪80年代所创立，他认为预测大致可分为2类：一类是以体系中各元素共性为依据的统计预测；另一类是以体系中各元素的特性为依据的信息预测（翁文波等，1996）。同时，他把客观存在的事件划分为常态子集和异态子集2类，前者中的事件是一般、经常、常规等有代表性事件，以数学期望、方差、均值等要素为统计量，应用概率统计原理和方法进行预测，这通常需要大样本量的支持，因此对于重大天灾等稀有事件的预测往往难以进行。而后者中的事件是异常、例外、特款等事件，它们的主要要素是信息，应用信息论原理和方法取得信息并进行预测。这2类预测的基本差别，翁文波精辟地概括为：从常态要素可作“统计预测”，以知其大概；从异态要素可作“信息预测”，以知其特性。

可公度法是一种信息预测方法，翁文波院士将可公度性预测方法应用到预测科学中，并曾利用可公度性信息对1976年唐山大地震、1982年华北干旱等现象做过成功预测，为重大自然灾害预测开辟了一条崭新道路，被国内外学者在自然灾害预测中广泛使用（门可佩，2009；刘铮瑶等，2014）。鉴于此，本文应用东北地区1900年以来M_S≥5.7地震资料，在可公度分析基础上，探讨了该区地震活动的发展趋势和可能的发震地点。

2 研究方法

常用的可公度计算方法有三元可公度法、四元可公度法和五元可公度法，相应公式（翁文波，1981）如下：

三元：N = a + (b - c)

四元：N = a + b + (c - d)，亦可写作：ΔX = a + b - c - d，则N =最后年份+ΔX

五元：N = a + (b - d) + (c-e)

式中，a、b、c、d、e为表 1中的历史地震年份，N为预测年份，同年度出现多次地震的只取第一个年份。

3 研究结果 3.1 时间对称性及趋势分析

根据1900年以来东北地区M_S≥5.7地震发生年份构建的可公度集X=﹛2018，2013，2003，1982，1980，1978，1975，1969，1960，1945，1944，1942，1941，1940，1922，1917，1902﹜，即x₁ = 2018，x₂ = 2013，…，x₁₃ = 1902。因此，利用三元可公度计算公式可以得到各个样本的三元可公度值，以据此进行预测。未来11年的三元、四元和五元可公度预测结果，均显示2023和2033年东北地区发生M_S≥5.7地震的趋势明显。

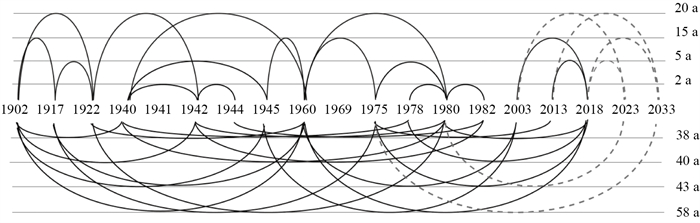
3.2 蝴蝶结构图分析

图 1为东北地区M_S≥5.7地震蝴蝶结构图，图中标注的数字为间隔年数。由图 1可发现，出现4次或以上的主周期有2 a、5 a、15 a、20 a、38 a、40 a、43 a和58 a。能够与2023年衍生的“蝴蝶结构”套合的主周期有5 a、20 a和43 a三种，与2033年有关的周期主要有15 a、20 a和58 a三种，二者均满足不漏报水平。因此，依据蝴蝶结构图判断2023和2033年东北地区都有可能发生M_S≥5.7地震，且2033年发震的可能性更大。

3.3 空间对称性及趋势分析

从1900年以来东北地区M_S≥5.7地震经纬向迁移（图 2）可看出，东北地区5.7级地震主要以（123.6°E，42.0°N）为对称轴，除个别年份外，震中经向迁移和纬向迁移具有较好的同步性，即当震中向西迁移时，纬度上则向南迁移；当震中向东迁移时，纬度上则向北迁移，即由西南→东北→西南往复迁移。由目前图像，推断下次地震往123.6°E以西和42.0°N以南迁移的可能性较大，即辽宁及环渤海地区地区。

4 结束语

本文基于1900年来东北地区M_S≥5.7地震资料，利用可公度法、蝴蝶结构图和可公度结构系图对未来东北地区5.7级地震进行趋势判断，同时分析了5.7级地震的空间分布及迁移规律。将可公度法和蝴蝶结构图相结合，可提高地震预测的准确性和未来趋势判断的可靠性。尽管如此，数学预测方法应用的毕竟是表象模式，更需要物理机制和方法的配合，因此，只有将可公度方法研究出的规律与物理预测相结合，才能更好地为防震减灾工作服务。