1 研究背景

许多著名学者一致认为自然正交函数方法是预测、评估和检验大规模数据中短期和长期变化的最先进工具（Dawson，2016；Chao，2019；Neha et al，2021）。然而自然正交函数方法最先应用在大气、气候和气象预测上（马开玉等，1993），近年来该方法逐渐应用在强震预测研究中。在中国，采用正交函数方法计算强震前的能量场（杨明芝，2004）、应变场（杨明芝，2017；罗国富，2023）和频次场（罗国富，2023），提取场的时间和空间异常信息，分析与强震的关系。在日本、印度以及欧美国家，采用经验正交函数方法计算强震前后的变形场（Chang，2011；Chao，2019；Neha et al，2021），分析强震的同震变形，给出三维变形的运动方向。

2 自然正交函数方法

（1）首先区域网格化。地震活动性分析中常以地震能量和地震频次为变量。本文分别把地震能量或者频次看作随机变量，通过自然正交函数方法，分解成空间和时间的函数，称为地震能量场或频次场。杨明芝（2004）提出用网格化方法构造地震活动场：假设某个研究区域，根据区域地震活动参数变量，选取一个时间间隔Δt，将研究的时间域划分为m个时段，t_i=Δt×i(i=1, 2, …, m)，将研究空间区域划分为n个相等的面积元Δs=Δx×Δy，其中心坐标为(x_j, y_j)(j= 1, 2, …, n)，分别统计各个时段内每一个面积元内的地震累计值，这个值可能是地震能量（或者把能量换算成应变），也可能是地震频次，并将这样的值作为代表研究区域时空坐标(x_j, y_j, t_j)(j= 1, 2, …, n)的地震活动场函数值。

（2）创建地震活动场。地震能量通过计算可以转化成地震应变，经过本团队近20年的不断探索，发现地震应变场比地震能量场在强震预测中具有更多的有优越性（杨明芝，2017），因此本文主要创建地震应变场和地震频次场。

地震应变场：以E表示地震释放的能量，$\sqrt{E}$表示为地震能量的平方根，根据地震能量的平方根与地震应变成正比，即$\sqrt{E}$= cε（c为地震震源相关参数，ε为震源区累积应变参数），这2个参数一定程度上反映了震源区的应变场变化。首先将区域网格化后，再以$S=\sum\limits_i \sqrt{E_i}$建立应变场函数，S_ij(i= 1, 2, …, m，j= 1, 2, …, n)是第j网格（代表空间）、第i时段（代表时间）的累计地震应变值，并表示为矩阵形式：

$ S=\left[\begin{array}{cccc} S_{11} & S_{12} & \ldots & S_{1 n} \\ S_{21} & S_{22} & \ldots & S_{2 n} \\ \vdots & \vdots & \vdots & \vdots \\ S_{m 1} & S_{m 2} & \ldots & S_{m n} \end{array}\right] $

(1)

地震频次场：以N表示地震活动频次，首先将区域网格化后，再以$N=\sum\limits_i N_{i j}$建立频次场函数，其中N_ij(i= 1, 2, …, m，j= 1, 2, …, n)是第j网格（代表空间）、第i时段（代表时间）的累计地震频次值并表示为矩阵形式：

$ N=\left[\begin{array}{cccc} N_{11} & N_{12} & \ldots & N_{1 n} \\ N_{21} & N_{22} & \cdots & N_{2 n} \\ \vdots & \vdots & \vdots & \vdots \\ N_{m 1} & N_{m 2} & \cdots & N_{m n} \end{array}\right] $

(2)

（3）自然正交函数计算。所谓自然正交函数展开，就是把应变场矩阵S（或者频次场矩阵N）分解成正交的空间函数x与正交的时间函数T乘积之和：

$ 应变场\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;S_{i j}=\sum\limits_{p=1}^n T_{i p} X_{p j}\left\{\begin{array}{l} i=1, 2, \cdots, m \\ j=1, 2, \cdots, n \end{array}\right. $

(3)

$ 频次场\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N_{i j}=\sum\limits_{p=1}^n T_{i p} X_{p j}\left\{\begin{array}{l} i=1, 2, \ldots, m \\ j=1, 2, \cdots, n \end{array}\right. $

(4)

应变场和频次场均满足正交和归一化条件，即

$ \sum\limits_{j=1}^n x_{k j} x_{l j}= \begin{cases}0 & k \neq l \\ 1 & k=l\end{cases} $

(5)

$ \sum\limits_{i=1}^m T_{i k} T_{i l}= \begin{cases}0 & k \neq l \\ \lambda_k & k=l\end{cases} $

(6)

通过求解应变场的协方差矩阵的特征方程R= S′S，或者频次场协方差矩阵的特征方程R= N′N，即

$ \left[\begin{array}{cccc} R_{11} & R_{12} & \cdots & R_{1 n} \\ R_{21} & R_{22} & \cdots & R_{2 n} \\ \vdots & \vdots & \vdots & \vdots \\ R_{n 1} & R_{n 2} & \cdots & R_{n n} \end{array}\right]\left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right]=\lambda\left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right] $

(7)

求解特征向量$\vec{x}_k$和特征值λ_k(k= 1, 2, …, n)。其时间因子表示为

$ 应变场\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vec{T}_k=S \vec{x}_k \quad k=1, 2, \cdots, n $

(8)

$ 频次场\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vec{T}_k=N \vec{x}_k \quad k=1, 2, \cdots, n $

(9)

特征向量$\vec{x}_k$代表了组成应变场或者频次场的不同场的地震应变空间分布，可以用来分析强震前的空间异常；而时间因子$\vec{T}_k$则代表了应变场或者频次场$\vec{x}_k$的时间变化，反映了震源周围不同时间活动场的动态特征，可以用来分析强震前的时间因子异常。

（4）地震应变场和频次场的异常提取方法。将协方差矩阵R的前几个特征值（由大到小排序）所对应的特征向量满足拟合总场的精度，表明前几个特征向量（应变场）叠加已经近似总应变场，这样研究前几个主要应变场的变化，代表了研究区域应变场的时空特征。假设n个特征值的和为b₀，用前l个主要场拟合总场的精度r_l为

$ r_l=\sum\limits_{p=1}^l \frac{\lambda_p}{b_0} $

(10)

式中，λ_p表示第p个特征根。

自然正交函数展开方法提取出前几个最大特征值相对应的应变场（或者频次场），相当于把区域应变场（或者频次场）的主要信息浓缩在前几个主要应变场（或者频次场），重点研究前几个应变场（或者频次场）的异常，排除无异常或与强震关联程度小的应变场（或者频次场）。集中研究这几个主要应变场（或者频次场）的时空异常变化，使研究问题简化。

3 研究结果 3.1 自然正交函数方法研究门源地区6级以上地震应变场

以地震应变场为变量，通过自然正交函数展开方法，计算1986年门源M_S 6.4地震、2016年门源M_S 6.4地震和2022年门源M_S 6.9地震前（简称3次强震）的地震应变场，提取出强震前应变场时间因子和空间等值线异常，研究已经发表在《Frontiers in Earth Science》，下载网址为（https://www.frontiersin.org/articles/10.3389/feart.2023.1152348/full）。

门源地区3次强震前时间因子在平稳背景上会出现超过均方差的高值或低值异常，异常主要集中在应变场的前4个典型场。通常在应变积累和应变释放两种等震线交汇区成为强震的潜在发生位置，强震发生后危险区逐渐消失。

3.2 自然正交函数方法研究中国大陆7级以上地震频次场

首次以地震频次作为地震活动变量，建立地震频次场，通过应用自然正交函数方法研究中国大陆1980年以来的9次7级以上大震的时空异常（罗国富，2023），结果发现在强震的地点预测中具有独特的优越性，最新的研究已经发表在《Frontiers in Earth Science》，下载网址为（https://www.frontiersin.org/articles/10.3389/feart.2022.992858/full）。

研究结果表明强震前时间因子超过一倍均方差的高值或低值异常，异常多数分布在频次场前4个典型场。区域频次等值线的高梯度旋涡区域是异常危险区，等值线值大于0.9且区域内具有活动断裂构造区域往往是强震发震部位。

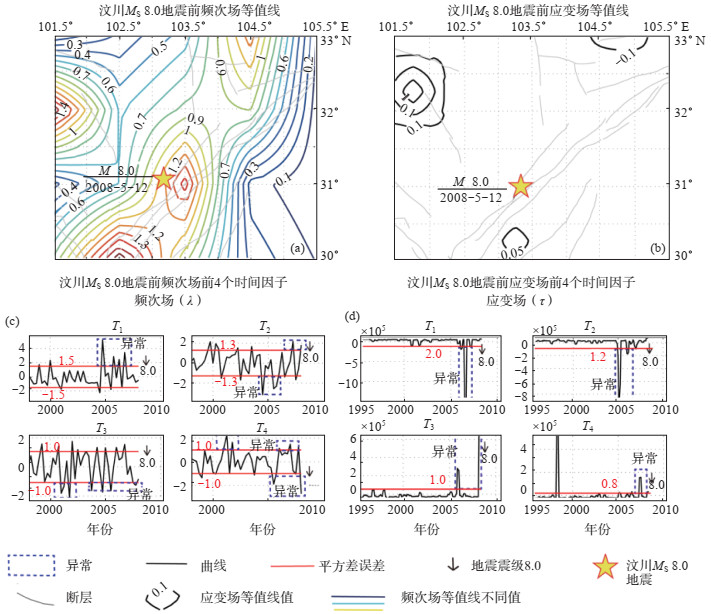
3.3 汶川M_S 8.0地震前频次场和应变场时空异常对比

通过自然正交函数方法，最新研究应变场与频次场时空异常差异。以汶川M_S 8.0地震为例（图 1），结果表明应变场易辨认时间因子异常，频次场对空间等值线异常了解更丰富。

4 结束语

本文详细介绍了自然正交函数方法以及在中国强震预测中的应用。该方法创建全新地震活动场，解决强震预测问题。抛弃以往过于强调概率统计的数学理论分析地震活动一面，通过创建地震活动场理论矩阵，用自然正交函数方法计算矩阵方程，提出地震应变和地震频次分别为变量的地震活动场时空函数，才可能真实描述地震活动随机特性。通过分析区域场的时空异常才有可能对强震的时间和地点做出较准确的预测。