2) 中国长沙 410016 中国冶金地质总局湖南地质勘查院
2) Hunan Geological Exploration Institute of China Metallurgical Geology Bureau, Changsha 410016, China
随着国民经济的日益发展,民众的生活水平逐渐提高,对出行安全的要求越来越高,作为高科技、高风险、高投入的航空机场,飞机的安全起降显得尤为重要。针对新建或运行多年的航空机场,应对机场跑道方位的地磁偏角及其年变率,进行初次测量或复核测量,以确保飞机起降安全,杜绝事故隐患,筑牢安全防线①。
① 中国民用航空局. 推动新型基础设施建设促进民航高质量发展实施意见. 中国民用航空局,2020.
当前,中国民航正以智慧民航建设为主线,推动行业数字化转型。在数字化转型过程中,精准、可靠的导航数据尤为重要,而机场地磁偏角是其中重要的基础数据,是不可忽略的。据《中国民航报》2021年11月29日报道,地球磁极每年都会发生有规律的改变,资料显示,自20世纪80年代开始,我国大部分机场的磁差数据、年变量和等磁差线均未更新,航迹偏差现象普遍存在,而飞机航线角度标识为磁航向,若磁差数据不及时更新,飞行程序误差将增大,严重威胁飞行安全。此外,若机场磁差的基础数据不更新,将导致与飞机导航数据库数据不匹配,引起惯性基准组件提供的航向与飞机自动飞行系统发生冲突,导致二类盲降或三类盲降仪表着陆来回摆动,飞机进近不稳定,长此以往,将直接威胁飞机的安全起降(梁永军等,2021)。
目前,中国地磁观测台站的绝对观测和相对记录比较完备,地磁绝对观测方法是F、D、I组合,一般采用质子磁力仪测量F值,用磁通门经纬仪(下文简称DI仪)获取D、I角度的差值,但DI仪测量时需要定标,即寻北,测量出的值是与标志之间的角度值,经后续计算获得真实的D和I值。DI仪一般采用指零法或近零法测量磁偏角、磁倾角(辛长江等,2003;顾左文等,2004)。指零法是,测量时传感器读数严格等于零,根据无磁经纬仪的度盘读数来计算磁偏角D和磁倾角I,其优点是可以直接用传感器的零输出、可忽略对仪器的线性度及格值的影响,但在机场、码头等野外测量时一般需要2人配合,人工指零与度盘读数无法做到同步,误差不可避免,因而较少采用。近零法是,将磁轴调到合适位置,使传感器输出至零位附近,在相对稳定时读取无磁经纬仪度盘读数,相对于指零法可缓解观测疲劳,但在磁场环境变化复杂时,近零位置追踪较为困难,测量效率相对偏低。因此,本研究提出采用DI仪分量测量法测量机场的磁偏角。
1 DI仪测量磁偏角的分量法DI仪是一种针对地磁的绝对观测仪器,由无磁经纬仪和磁通门检测系统2大部分构成,一般采用近零法测量磁偏角。其中,磁通门检测系统由传感器(近接收)、电路、显示屏和电源等部分组成,传感器(远接收)安装在无磁经纬仪横轴(望远镜)的上部。磁通门检测系统的其他部分装在一个机箱内,为减少磁场干扰,建议观测者在观测时将其置于无磁经纬仪2 m之外,通过输出电压的零位显示,确定传感器轴向的正确位置。DI仪近零法测量磁偏角在仪器操作手册②及相关文献(辛长江等,2003;顾左文等,2004)都有叙述,在此不再赘述。
② 北京市京核鑫隆科技有限责任公司. JHC6E-DI磁力仪使用说明书. 2019.
事实上,使用DI仪,除了可以采用近零法、指零法测量磁偏角D、磁倾角I外,还可以测量任意方向的磁场强度。如图 1所示,若测量出地理N向、地理E向的磁场分量X、Y,就可计算出磁偏角D、磁场水平分量H;若进一步观测到向下的磁场分量Z,就可以计算出磁倾角I、磁场总强度F,公式如下
| $ \left\{\begin{array}{l} D=\arctan (Y / X) \\ H=\sqrt{X^2+Y^2} \\ I=\arctan (Z / H) \\ F=\sqrt{X^2+Y^2+Z^2} \end{array}\right. $ | (1) |

|
图 1 地磁场观测分量 Fig.1 Observation component of geomagnetic field |
为消除或削弱无磁经纬仪的视准轴误差、横轴误差、度盘分划误差,以及磁通门轴与视准轴不平行等仪器误差,分量测量法采用以下观测与计算方法,具体观测流程见图 2。
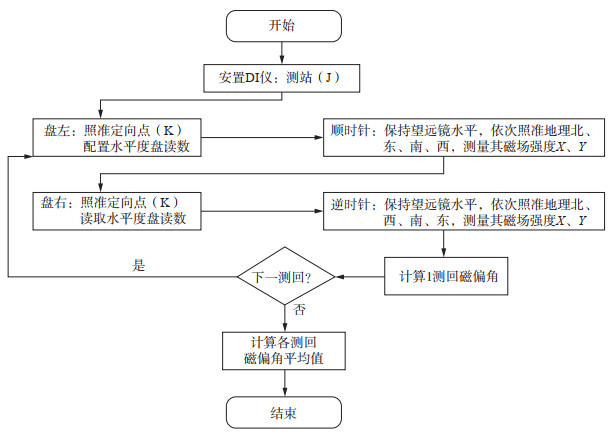
|
图 2 分量法测量磁偏角流程 Fig.2 Flow chart of measuring magnetic declination using the component method |
(1)准备工作。选择测站点(J)和定向点(K),二者相距200 m以上,其中测站及其附近无明显的外界磁场干扰;用GNSS-RTK测量出J、K的直角坐标(xJyJ,xKyK)以及测站点J的经纬度LJ、BJ,计算坐标方位角αJK、测站点J的子午线收敛角γJ以及定向真方位角AJK,公式如下
| $ \left\{\begin{array}{l} \alpha_{\mathrm{JK}}=\arctan \left(\left(y_{\mathrm{K}}-y_{\mathrm{J}}\right) /\left(x_{\mathrm{K}}-x_{\mathrm{J}}\right)\right) \\ \gamma_{\mathrm{J}}=\left(L_{\mathrm{J}}-L_0\right) \times \sin B_{\mathrm{J}} \\ A_{\mathrm{JK}}=\alpha_{\mathrm{JK}}+\gamma_{\mathrm{J}} \end{array}\right. $ | (2) |
(2)在测站点(J)上安置无磁经纬仪,使用专用电缆线连接传感器与磁通门检测系统的电路装置,打开磁通门检测系统的电源开关,利用按键开关检验电源电压。
(3)盘左瞄准定向点(K)标志,配置水平度盘读数为AJK + τ,其中AJK为定向真方位角、τ为水平度盘读数配置误差。
(4)顺时针转动照准部,依次照准地理N、地理E、地理S、地理W向,分别读取并记录磁场强度XLN、YLE、XLS、YLW(注意,读取磁场强度前要松开自动补偿器锁紧轮,并调节垂直度盘读数为90°00′00″)。
(5)盘右瞄准定向点(K)标志,读取水平度盘读数(设为:AJK + τ ±180°+ 2c,其中c为仪器视准轴误差)。
(6)逆时针转动照准部,依次照准地理N、地理W、地理S、地理E向,分别读取并记录磁场强度XRN、YRW、XRS、YRE(注意,读取磁场强度前要松开自动补偿器锁紧轮,并调节垂直度盘读数为270°00′00″)。
(7)完成1测回观测、计算工作,得到
| $ \left\{\begin{array}{l} \bar{X}=\left(X_{\mathrm{LN}}-X_{\mathrm{LS}}+X_{\mathrm{RN}}-X_{\mathrm{RS}}\right) / 4 \\ \bar{Y}=\left(Y_{\mathrm{LE}}-Y_{\mathrm{LW}}+Y_{\mathrm{RE}}-Y_{\mathrm{RW}}\right) / 4 \\ D=\arctan (\bar{Y} / \bar{X}) \end{array}\right. $ | (3) |
式中,X、Y、X、Y的单位均为纳特(nT),D的单位为弧度。
若要消除水平度盘分划不均匀误差,可采用多个测回(n)开展测量工作,重复步骤(2)—(7),只需在盘左瞄准定向点配置水平度盘读数时,每测回增加180°/n即可。
1.2 精度分析设地理N向、地理E向的磁场分量X、Y一次观测中误差为mX、mY,则可运用误差理论的基本知识(朱建军等,2013)进行精度评定,1测回中误差计算公式如下
| $ \left\{\begin{array}{l} m_{\bar{X}}=\frac{m_X}{2} \\ m_{\bar{Y}}=\frac{m_Y}{2} \\ m_D^2=\left[\left(\frac{\bar{Y}}{\bar{X}^2+\bar{Y}^2}\right)^2 m^{2 / x}+\left(\frac{\bar{X}}{\bar{X}^2+\bar{Y}^2}\right)^2 m^{2 / Y}\right] \times \rho^2 \end{array}\right. $ | (4) |
式中,X、Y、mX、mY、mX、mY的单位为纳特(nT),mD的单位为角秒,ρ为1弧度所对应的角秒数。
2 实例磁差观测工作受多种因素的影响,主要包括太阳活动(黑子、耀斑、日冕物质抛射等)、地表输变电及通信设施、测站周围的铁磁性物质等(徐文耀,2009)。为验证分量法测量磁偏角的有效性,选择一个地磁观测条件良好的地点、时间窗口,同时采用近零法、分量法测量磁偏角,以作为对比。所用仪器是北京市京核鑫隆科技有限责任公司生产的JHC6E-DI仪(编号为W1903),主要性能参数②见表 1。
② 北京市京核鑫隆科技有限责任公司. JHC6E-DI磁力仪使用说明书. 2019.
| 表 1 JHC6E-DI仪的主要性能参数 Table 1 Main performance parameters of JHC6E-DI instrument |
2023年5月13日,在江西省赣州市某机场进行磁偏角测量,测站点、定向点仪器设备安置见图 3。

|
图 3 仪器设备安置 Fig.3 Placement diagram of instrument and equipment |
据前文所述观测、计算步骤,得到DI仪基于分量法、近零法的磁偏角测量及计算结果,见表 2、图 4。
| 表 2 DI仪分量法、近零法磁偏角测量记录计算表 Table 2 Calculation table for magnetic declination measurement records of the DI magnetometer component method and the near zero method |

|
图 4 DI仪分量法、近零法磁偏角测量结果对比 Fig.4 Comparison of magnetic declination measurement results between the DI magnetometer component method and the near zero method |
由表 2、图 4可知,本次实验使用同一台DI仪,在同一地点分别采用分量法、近零法进行磁偏角测量,同一测回互差、各测回平均值互差均较小,测量结果是吻合的,表明利用DI仪测量磁场分量X、Y,并计算磁偏角的方法是可行的。
2.2 精度分析影响磁场分量X、Y测量精度的因素主要有观测者、仪器及外界环境3个方面。磁场强度是时间、位置的复杂函数,文中仅探讨DI仪测量磁场分量X、Y计算磁偏角的可行性,且主要与近零法结果进行比较,而采用2种方法测量磁偏角时均受到外界环境的影响,故暂不讨论。文中讨论其他观测误差,包括定向真方位角误差、对中误差、照准误差、度盘配置误差、估读误差等,对观测精度的影响。
(1)定向真方位角的影响。测站点J、定向点K的坐标由网络RTK测量得到,据相关测量规范,其点位中误差小于±2 cm,设两点间距离为S(下同),则
(2)对中误差的影响。在测站点J、定向点K均存在对中误差,设对中误差均为2 mm,则由此产生的水平方向误差约为
(3)照准误差的影响。配置水平度盘前,经纬仪应严格照准定向点标志,设照准误差为2 mm,则由此产生的水平方向误差约为
(4)度盘配置误差的影响。本次实验的仪器为6″级经纬仪,水平度盘配置时会存在误差,其最大值为m配置 = ± 3"。
(5)估读误差的影响。6″级经纬仪估读误差为m估读 = ± 6′。
以上5项误差是相互独立的,根据误差处理过程中的等影响原则及误差传播定律,其综合影响为
| $ m_{\text {观测 }}= \pm \sqrt{m_{A_{\mathrm{JK}}}^2+m_{\text {对中 }}^2+m_{\text {照准 }}^2+m_{\text {配置 }}^2+m_{\text {估读 }}^2} $ | (5) |
参照公式(4)第3项,在假设m观测对mX、mY的影响一样时,可将上述m观测(单位″)转换为对磁场分量X、Y的影响(单位nT)。
因测试地区的地理N向、地理S向磁场分量较大,JHC6E-DI仪的地理N向、地理S向磁场分量只能显示至0.01 μT,因此,由数据显示产生的误差为:mX显 = ±5 nT、mY显=±0.05 nT,进而得到:
| 表 3 DI仪分量法磁偏角测量误差分析 Table 3 Analysis of measurement error of magnetic declination using the DI magnetometer component method |
上述误差分析表明,采用分量法测量磁偏角,其精度满足相关规范要求③。
③ 中国民用航空局. MH/T 5025 — 2011民用机场勘测规范. 2011.
3 结论DI仪测量磁偏角的分量法有如下优点及注意事项:
(1)相对于近零法,采用分量法测量磁偏角,因无需追踪磁场零位,野外测量工作较为简便,若在DI仪磁通门检测系统上加装自动计时、自动记录装置,可实现单人作业,进一步提高工作效率。
(2)DI仪可以观测磁场Z分量,进而可获取该地地磁场所有7个分量。
(3)要提高分量法测量磁偏角的精度,需要提高测站点、标志点坐标测量精度,且此两点间距离不宜小于200 m,同时应加快测量速度、尽量缩短1测回观测时间,还要注意望远镜指向与磁通门检测系统读取磁场强度的同步性。
综上所述,利用DI仪所测的磁场分量X、Y来计算磁偏角是可行的,其精度与近零法相当,可以满足相关磁偏角测量规范和工作要求,具有一定推广应用价值。
顾左文, 周勋, 高金田, 等. 用近零同步观测法进行DI磁力仪的比测[J]. 地震地磁观测与研究, 2004, 25(5): 11-17. |
梁永军, 冯智君. 国内机场磁差数据情况调查: "差"之毫厘, 失之千里[N]. 中国民航报, 2021-11-29.
|
辛长江, 沈文荣, 李秋红, 等. 指零法和近零法观测基线值对比分析[J]. 地震地磁观测与研究, 2003, 24(1): 77-80. |
徐文耀. 地球电磁现象物理学[M]. 合肥: 中国科学技术大学出版社, 2009: 37-51.
|
朱建军, 左廷英, 宋迎春. 误差理论与测量平差基础[M]. 北京: 测绘出版社, 2013: 16-27.
|
 2023, Vol. 44
2023, Vol. 44

