2) 中国内蒙古自治区 026000 锡林浩特地震监测中心站
2) Xilinghot Earthquake Monitoring Center Station, the Nei Mongolia Autonomous Region 026000, China
地震目录是记录一段时间内所有地震事件的基础数据,包括地震的时刻、地点、震级等信息。它是地震学研究和应用的基础资料之一,也是地震灾害评估及防范工作中不可或缺的数据来源。最小完整性震级(Minimum Completeness Magnitude,简称Mc)是指某个地震目录在一定的空间范围和时间区间内所记录到的所有地震事件中最小的一个可靠检测到的震级。Mc值可以用来评估该地震目录的完整性和真实性。研究表明,地震台站的分布、布局和密度、仪器设备的精度以及震相数据的信噪比等因素会影响地震事件的检测和定位,从而影响到地震目录的完整性和质量(Woessner et al,2005;蒋长胜等,2008;王琼等,2011),因此,Mc值是衡量地震目录完整性和质量的重要参数之一。
本文选取中国台网中心地震目录中1970—2022年赤峰—通辽地区地震数据作为基础资料,采用最大曲率法、拟合度检测法和震级—序号法计算研究区域不同时间段最小完整性震级Mc。
1 背景资料 1.1 地质构造背景赤峰—通辽地区位于内蒙古东部地区(116°—124°E,41°—46°N),处于大兴安岭断裂隆起区和EW向燕山断裂隆起区松辽盆地西南部,具有隆凹相间的盆地结构。断层以EW向展布为主,断裂发育,独特的“枝干型”断裂体系,使其构造环境具有较强的特殊性。该地区属于中、小地震活动较多的地带,且具有与活动断层的分布相符的微地震活动条带,处于NEE向的压力场中,与中国东部一体化,为该区历史和近代中强地震的形成奠定了良好的地理环境(韩晓明等,2009)。该区域具有中、强地震的构造环境。
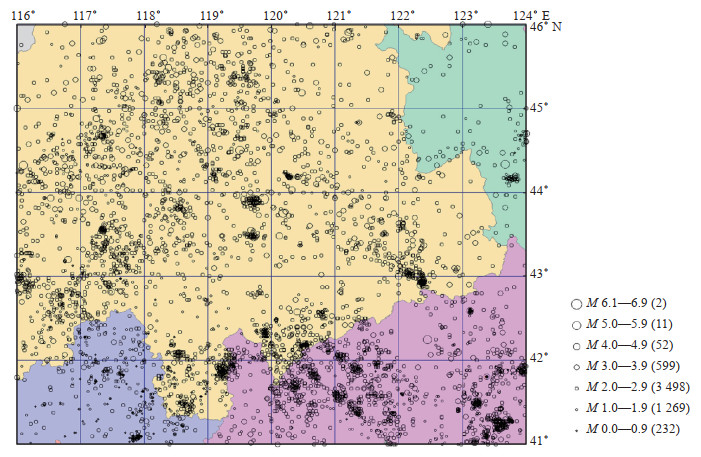
1.2 地震活动统计据中国地震台网中心地震目录,1970—2022年,赤峰—通辽地区地震事件共5 663个,其中:ML<2.0地震事件1 501个,约占目录总数的26.5%;ML 2.0—3.9的地震事件4 097个,约占目录总数72.3%;ML≥4.0地震事件65个,仅占比约1.2%。赤峰—通辽地区1970—2022年地震分布见图 1。
|
图 1 赤峰—通辽地区地震分布(1970—2022年) Fig.1 Distribution of earthquakes in Chifeng-Tongliao area (1970-2022) |
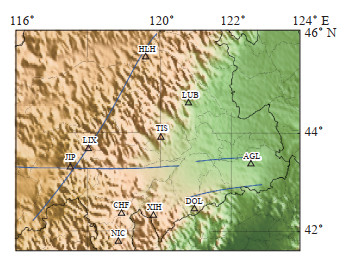
赤峰—通辽地区现有地震监测台站10个,台站分布见图 2。其中林西台(LIX)、天山台(TIS)1985年前后开展地震监测工作,大沁他拉台(DQL)2010年以后建成并投入使用,其他台站均为1975年建成并开始地震监测工作。2000年以前赤峰—通辽地区监测台网均为模拟地震记录;1997年“九五”改造后,启动数字化地震观测系统;2010年前后,随着“十五”数字化地震观测系统项目的完成,全部台站配备宽频带和甚宽频带地震计,并开始地震目录编目工作,地震监测能力有了大幅度提升。
|
图 2 赤峰—通辽地区地震台站分布 Fig.2 Distribution of seismic stations in Chifeng-Tongliao area |
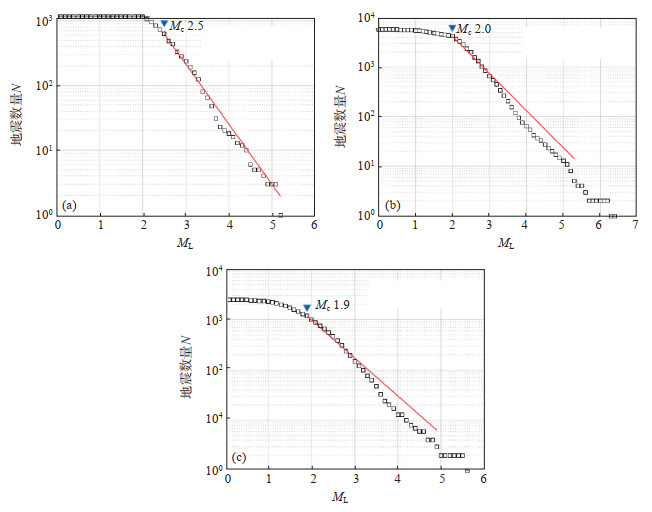
最大曲率法是一种无参数计算Mc值的方法,这种方法的计算简便快捷(Wyss et al,1999;Wiemer et al,2000)。通过对震级—频度分布曲线一阶导数计算,找出一阶导数的最大值,即曲率首次发生突变的转折点作为Mc的值。由于1970—2009年地震目录未收录ML<2.0的地震事件,1985年以前的地震事件记录不完整,因此将1970年以来的地震目录分为1970—1985年、1986—2009、2010—2022年3部分绘制G—R关系曲线,结果见图 3。
|
图 3 赤峰—通辽地区不同时段震级—频度关系 (a)1970—1985年;(b)1986—2009年;(c)2010—2022年 Fig.3 G-R relation curves of earthquake catalogs in different periods in the Chifeng-Tongliao area |
由图 3(a)可见1970—1985年最小完整性震级Mc为ML 2.5。由图 3(b)可见1986—2009年最小完整性震级Mc为ML 2.0。由图 3(c)可见,2010—2022年最小完整性震级Mc为ML 1.9。
2.2 拟合度检测法拟合度检测法(GFT)是地震学中一种常用的用于确定最小完整性震级Mc值的方法,该方法基于震级—累积频度分布的比较,将真实地震目录与拟合的震级—累积频度分布进行比较,从而计算Mc值(Wiemer et al,2000;Woessner et al,2005)。GFT需要计算每个震级档里实测的事件数量与拟合曲线估计的事件数量之间的差值与实际观测事件数量的比值R。选取不同截止震级Mi,计算实际观测目录中M≥Mi事件的G—R关系的a值(记为ai)和b值(记为bi),并据此生成拟合累积分布曲线,则R值计算公式如下
| $ R\left(a_i, b_i, M_i\right)=1-\frac{\sum\limits_{M_k=M_i}^{M_k=M_{\max }}\left|B_k-S_k\right|}{\sum\limits_{M_k=M_i}^{M_k=M_{\max }} B_k} $ | (1) |
式中,Bk和Sk分别为截止震级Mi与最大震级Mmax之间某一震级档Mk的实际观测事件和拟合曲线估计事件的累积数量。一般取R值达到给定的拟合度(如R = 90%或R = 95%)或R值达到最大值时首个截止震级Mi作为Mc的值。Mc值的选取按照GTF-95%→GTF-90%→MAXC的优先级确定,Mc值的选取见图 4(a)中Mc-Best的黑色曲线所示。
|
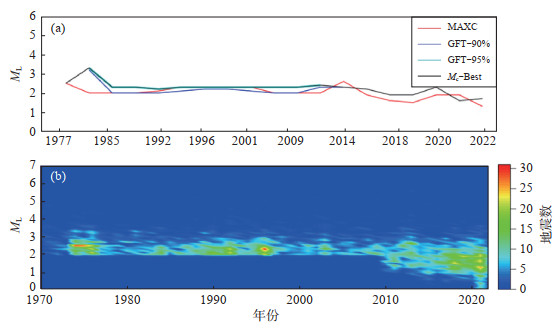
图 4 赤峰—通辽地区地震目录最小完整性震级采用拟合度检测法和震级—序号法的评估结果 (a)拟合度检测法分析评估赤峰—通辽地区地震目录最小完整性震级的时间演化;(b)震级—序号法评估赤峰—通辽地区地震目录最小完整性震级 Fig.4 The evaluation results of the minimum magnitude of completeness of the earthquake catalog in the Chifeng-Tongliao area using the goodness-of-fit test method and the magnitude-sequence-number method |
由图 4(a)可见,1970—1985年最小完整性震级Mc约为ML 2.5—3.5;1986—2009年最小完整性震级Mc约为ML 2.1—2.4;2010—2022年最小完整性震级Mc约为ML 1.6—2.4。
2.3 震级—序号法震级—序号法将地震事件以时间为序,并将其归类。通过计算和可视化处理各组中每个震级档所发生的地震数目,可以显示出Mc数值随时间的变化特征(Ogata et al,1991;Huang,2006)。与震级—时间分布相比,震级—序号分布不仅能够避免观测到大量余震或震群等聚集事件,还能够反映短时间内台网监测能力的变化。采用震级—序号法评估赤峰—通辽地区1970—2022年地震目录最小完整性震级,结果见图 4(b)。由图 4(b)可见,1970—1985年最小完整性震级Mc约为ML 2.0—3.0;1985—2010年最小完整性震级Mc约为ML 2.0—2.4;2010—2022年最小完整性震级Mc约为ML 1.3—2.1。
3 结论通过对研究区域地震目录的研究,采用最大曲率法、拟合度检测法、震级—序号法进行对比计算,可见3种方法的计算结果基本吻合,在地震事件较少情况下,采用拟合度检测法计算,结果偏大,而采用最大曲率法的计算结果,整体较其他2种方法要小。综合3种方法的计算结果及监测台站的建设过程可知,由于研究区域1970—1985年台网建设尚未完成,同时资料保存并不完整,因此最小完整性震级偏大,约为ML 2.0—3.5;1985—2010年观测相符稳定,最小完整性震级Mc约为ML 2.0—2.4;2010—2022年由于地震台网数字化的完成以及编目工作的开始,地震数据记录更加完整,最小完整性震级呈逐渐下降趋势,约为ML 1.3—2.4。
韩晓明, 王鑫, 郝美仙. 赤峰-辽蒙交界地区地震活动性及平均波速比分析[J]. 高原地震, 2009, 21(3): 11-16. |
蒋长胜, 吴忠良, 李宇彤. 首都圈地区"重复地震"及其在区域地震台网定位精度评价中的应用[J]. 地球物理学报, 2008, 51(3): 817-827. |
王琼, 曲延军, 高歌, 等. 新疆天山南部构造区不同时段小地震目录完整性分析[J]. 地震研究, 2011, 34(1): 35-41. |
Huang Q H. Search for reliable precursors: A case study of the seismic quiescence of the 2000 western Tottori prefecture earthquake[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B4): B04301. DOI:10.1029/2005jb003982 |
Ogata Y, Imoto M, Katsura K. 3-D spatial variation of b-values of magnitude-frequency distribution beneath the Kanto District, Japan[J]. Geophysical Journal International, 1991, 104(1): 135-146. DOI:10.1111/j.1365-246X.1991.tb02499.x |
Wiemer S, Wyss M. Minimum magnitude of completeness in earthquake catalogs: Examples from Alaska, the western United States, and Japan[J]. Bulletin of the Seismological Society of America, 2000, 90(4): 859-869. DOI:10.1785/0119990114 |
Woessner J, Wiemer S. Assessing the quality of earthquake catalogues: estimating the magnitude of completeness and its uncertainty[J]. Bull Seismol Soc Am, 2005, 95(2): 684-698. DOI:10.1785/0120040007 |
Wyss M, Hasegawa A, Wiemer S, et al. Quantitative mapping of precursory seismic quiescence before the 1989, M 7.1 off-Sanriku earthquake, Japan[J]. Annals of Geophysics, 1999, 42(5): 851-869. DOI:10.4401/ag-3765 |
 2023, Vol. 44
2023, Vol. 44

