0 引言

城市地铁在运行过程中会产生杂散电流，引起地表电位发生变化甚至可能产生一定程度的危害，如对轨道旁通讯设备产生电磁干扰(李智宇，2022)，对埋地金属管线带来腐蚀危害(张献伟，2021)，为此相关部门从防护设计、监控、检验、测试、验收等方面出台了《CJJT49—2020地铁杂散电流腐蚀防护技术标准》(中华人民共和国住房和城乡建设部，2020)。对于以捕捉弱地震异常电磁信号为目标的地电观测来说，有效识别和排除地铁杂散电流对地电观测的影响，是当下地震前兆观测亟待解决的一个难题，对地震前兆观测及地震预测研究具有重要意义。

针对地铁运行产生杂散电流的问题，研究者建立了“轨道—大地”模型，从理论上分析和计算了杂散电流(程浩，2019；陈瑶，2020)；分析了杂散电流引起的电化学腐蚀现象(孙军溪等，2006；丁海涛等，2010；王承涛，2020；王爱民，2021)和变压器偏磁特征(伍俊伶，2022)；通过仿真模拟，计算了杂散电流引起的电位波动区间，评估了杂散电流的干扰范围与程度(倪砚茹等，2022)；根据杂散电流的分布规律和特点，提出了相应的防护措施(徐文宽，2021；关卓然，2021)。特别是针对杂散电流在地震前兆观测的实际运用中，研究人员分析了杂散电流对电磁观测影响的特征(谢凡等，2011；樊晓春等，2021；王兰炜等，2023)，给出了降低地铁对地电观测干扰的处理方法(张世中等，2013；席继楼等，2013)，研制了地电阻率交流抗干扰观测设备(王兰炜等，2019)，提出了深埋电极缩短极距从而减小干扰的措施(聂永安等，2010；解滔等，2019)。前人工作为开展地铁杂散电流产生机理、分布规律及防护措施等方面的研究打下了良好基础。

据国家地电台网中心(地电站网运行管理与产品服务平台)统计，全国在网运行的地电观测仪器共计203台(套)，其中地电阻率观测数据优秀率为83.14%，地电场观测数据优秀率仅为68.81%，造成地电场数据内在质量不高的主要原因是观测环境受到破坏和其他不可控因素，例如分布在具有轨道交通(地铁)的大城市周边的观测站，普遍受到地铁杂散电流的干扰。近年来我国城市轨道交通网络建设发展迅速，首都圈、华东和华南等地区的大部分地电观测均不同程度受到轨道交通运行的干扰。以天津塘沽地震台(下文简称塘沽台)为例，该台地电场观测受地铁干扰，地铁停运和运行时段的信噪比相差近3倍，观测数据日精度高于地震地电阻率观测规范要求的＜0.3%(其中NS向日精度年均值达1.62%，EW向日精度年均值达0.39%)。2022年天津地铁Z2线开工建设，该线路自东向西从塘沽台地电阻率测区NS向测量极与供电极之间穿过，车务段紧邻测区西侧规划建设。受地域限制无法进行台址搬迁，只能在现有条件下进行改造。

针对轨道交通干扰问题，本研究以天津塘沽台地电阻率观测为例，选取距台站最近、造成显著干扰的天津地铁9号线，采用“轨道—大地”模型，结合地铁“日行夜停”的特点，对自然电位数据进行分段研究，计算地铁9号线运营产生的杂散电流理论值，与地电阻率观测数据进行对比，从而为评估地铁运行对地电观测的影响及提出“因台施策”改造方案提供理论依据。

1 自然电位观测的主要影响因素

自然电位法最早应用于矿产勘探，是一种被动源地球物理勘探方法，当前认为地壳局部物理、化学条件变化是自然电位产生异常的主要原因(李金铭，2005；Xie et al，2023)。在排除地震前兆异常前提下，以下几种因素可能会对自然电位产生影响：①农业灌溉；②短时强降雨；③工频干扰；④浅水位变化；⑤地铁轨道漏电。其中，前3种干扰具有明显的变化特征，一般持续时间较短，易于识别；第4种干扰属于季节性变化，具有明显的年变化规律；地铁轨道漏电干扰连续不断，具有明显日变规律。因此，在某一观测场地无局部物理、化学条件变化时自然电位比较稳定(夏昭，2015；查楠等，2018；锡振强，2019；王丽红等，2021)。

在进行地电阻率观测前需观测自然电位，并在测量人工电位差时予以剔除，其主要目的是对测区自然电场大小进行估计，最大限度地使人工电位差完全来源于两供电极所形成的稳恒电流场。自然电位仅需在地电阻率观测前进行单次测量，当测区内无灌溉、大功率用电或降雨等干扰时，其变化基本恒定。

2 地铁杂散电流产生机理与理论计算 2.1 地铁杂散电流的形成机理

出于对换乘方便、调速快捷、机械性能好等多方面考虑，我国地铁列车一般采用直流供电牵引制式运行，电流由牵引变电所正极流出，通过接触网向地铁列车供电，最后通过走行轨回流到牵引变电所负极[图 1(a)]。钢轨扣件是保证走行轨与大地之间电气绝缘的主要构件，但扣件的绝缘效果有限，部分电流会泄漏至大地形成杂散电流，从而产生电场，叠加在地铁线路周边自然电场之上。

2.2 地铁杂散电流的理论计算

如图 1(b)所示，地铁在轨道上运行时牵引电流在“牵引变电所正极—接触网—地铁列车—轨道—牵引变电所负极”这一闭合回路内流动。轨道通过钢轨扣件、枕木固定在路基上，城市轨道交通钢轨扣件间距在0.6—0.7 m，1 km地铁线路钢轨扣件达3 000多个，绝缘性能难以长时间保持一致，当电流流经轨道时部分电流经钢轨扣件流入地下，形成杂散电流。随着地铁线路的延长，电流流经多个节点，并沿轨道回流至牵引变电所负极或者沿钢轨扣件流入地下，其总量保持不变，且流入和流出某一漏电节点的代数和为零，满足基尔霍夫定律，即在牵引系统所形成的闭合回路中，沿回路绕行方向，任一瞬间的各段电压代数和恒等于零，流入某个节点的电流之和等于流出该节点的电流之和(李永刚等，2005；孙军溪等，2006；赵宇辉等，2009；李雷等，2019；李怀志，2020)。

根据《CJJT49—2020地铁杂散电流腐蚀防护技术标准》(中华人民共和国住房和城乡建设部，2020)，设I为地铁列车的负荷电流，单位A；L为地铁列车到牵引变电所负极回流点的距离，单位km；X为测量泄漏点到牵引变电所负极回流点的距离，单位km；R_g为轨道的纵向电阻，单位Ω/km；R′_g为轨道对大地的过渡电阻，单位Ω/km；I_g(x)为测量泄漏点x处的轨道返回电流，单位A；I_d(x)为测量泄漏点x处流入大地的杂散电流，单位A；u_g(x)为测量泄漏点x处的轨道电位，单位V。

如图 1(c)所示，在由轨道、两钢轨扣件及大地所形成的回路中，电压有如下关系

$I_{\mathrm{g}}(x) R_{\mathrm{g}} \mathrm{d} x+u_{\mathrm{g}}(x)-\left[u_{\mathrm{g}}(x)+\mathrm{d} u_{\mathrm{g}}(x)\right]=0 $

(1)

如图 1(d)所示，在轨道与大地所形成的节点，电流有如下关系

$ \mathrm{d} I_{\mathrm{g}}(x)=\frac{u_{\mathrm{g}}(x)}{R_{\mathrm{g}}^{\prime} / \mathrm{d} x} $

(2)

当漏电点位于列车起点和终点时，若出现漏电，则漏电电流I_g(x) = I，令$\alpha=\sqrt{R_{\mathrm{g}} / R_{\mathrm{g}}^{\prime}} $，可求得返回牵引变电所负极的返回电流，又因返回电流中I_g(x)和杂散电流I_d(x)满足I_g(x) + I_d(x) = I的关系，可求得杂散电流

$\begin{aligned} I_{\mathrm{d}}(x) & =I-\frac{I R_{\mathrm{g}}\left(1-\mathrm{e}^{-\alpha L}\right) \mathrm{e}^{\alpha x}-I R_{\mathrm{g}}\left(1-\mathrm{e}^{\alpha L}\right) \mathrm{e}^{-\alpha x}}{R_{\mathrm{g}}\left(\mathrm{e}^{\alpha L}-\mathrm{e}^{-\alpha L}\right)} \\ & =I\left(1-\frac{R_{\mathrm{g}}\left(1-\mathrm{e}^{-\alpha L}\right) \mathrm{e}^{\alpha x}-R_{\mathrm{g}}\left(1-\mathrm{e}^{\alpha L}\right) \mathrm{e}^{-\alpha x}}{R_{\mathrm{g}}\left(\mathrm{e}^{\alpha L}-\mathrm{e}^{-\alpha L}\right)}\right) \end{aligned} $

(3)

式中：I为电动列车取流；L为电动列车到直流牵引变电所的负极回流点的距离；R_g为轨道的纵向电阻；R′_g为轨道对大地的过渡电阻。

3 杂散电流理论计算与实际观测值对比 3.1 研究线路选取

截至2022年年底，天津共开通7条地铁线路，其中地铁1号线设高架站，2号线、9号线设有高架站和地面站，地面站与高架站之间有地面铺设线路。

据《B50157—2013地铁设计规范》(中华人民共和国住房和城乡建设部，2014)《CJJT49—2020地铁杂散电流腐蚀防护技术标准》(中华人民共和国住房和城乡建设部，2020)，地下站和高架站一般设置在城区，地面站一般设置在城区外，多采用“走形轨”回流，产生杂散电流的可能性更大。由杂散电流产生机理可知，轨道交通地面线路产生杂散电流的可能性最大，且已有观测实践证明，天津地铁9号线是塘沽台地电阻率观测最强干扰源，故选择其地面线路段作为研究对象，主要原因如下：①9号线由地下、高架、地面线路构成，线路长，其中易产生杂散电流的地面线路长度达5 km[图 2(a)中红色线]；②9号线地面线路段位于塘沽台正南方向约6 km，与该台地电阻率NS向测道几乎垂直[图 2(a)、(b)]，可用点电流源电位模型进行分析；③紧邻9号线地面线路段南侧车务段[图 2(c)]，是易被忽视的重要干扰源之一。

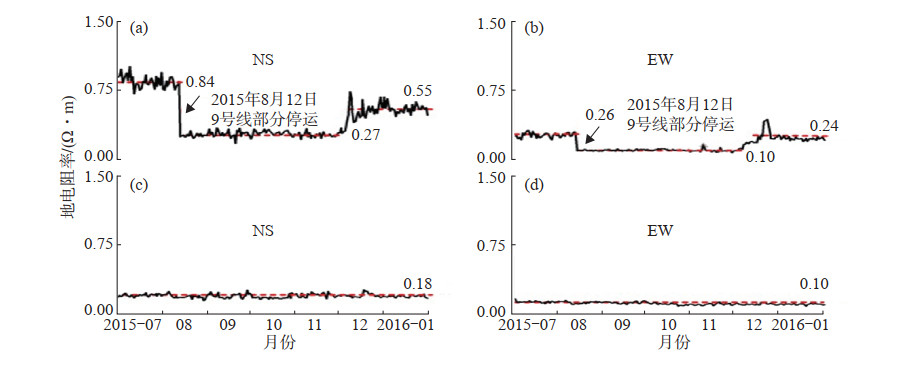
图 3所示为2015年8月12日天津港发生爆炸前后塘沽台、青光台(两台地下介质电性结构相近)地电阻率均方差日均值对比曲线，可见：在9号线中山门—东海路线路段停运期间，塘沽台均方差明显降低，与青光台相当(NS向略高，与塘沽台NS向电极距长于青光台有关)。停运前后，塘沽台NS向地电阻率均方差下降达0.57 Ω·m，EW向下降达0.29 Ω·m，证明地铁9号线运行对塘沽台地电阻率造成较大干扰。

3.2 地面段杂散电流计算

为方便计算，仅考虑一台地铁列车在2个车站之间的运行。列车运行电流取4 000 A，列车到牵引变电所负极距离取0—5 km，轨道纵向电阻取0.038 Ω·m，过渡电阻取30 Ω·m(天津市轨道交通设计部门提供)，代入式(3)，求得地铁列车在此段线路运行时产生杂散电流的大小。由地铁9号线列车通过地面线路钢管公司站—胡家园站时杂散电流(I_d)—漏电点至负极回流点(X)—列车至负极回流点(L)关系图(图 4)可知，杂散电流受地铁列车所处位置和漏电点所在位置的共同影响，列车距负极回流点越远，漏电点距负极回流点越近，牵引变电所正负极越长，杂散电流越大，当X = L时，杂散电流为0。当9号线单列列车通过5 km长的地面线路时，杂散电流最高可达50 A(图 4)。

3.3 地电阻率供电与杂散电流电位分析

地电阻率观测通过2个埋入地下的电极供入恒定电流，同时获取2个埋入地下的测量极之间的电位，进而求得地电阻率。塘沽台地电阻率NS向供电极距1 500 m，测量极距500 m，采用对称四极法布设，装置系数K = 3 142 m，供电电流2 A，几乎与地铁9号线路垂直，直线距离约6 km[图 2(a)、(b)]。将A₁、B₁两个供电电极与电源相连，并向地下供入强度为I的电流时，根据点电流源在半无限空间的计算公式，可求得测量极M₁、N₁处的电位差，公式如下

$ \Delta U_{\mathrm{M}_1 \mathrm{~N}_1}=U_{\mathrm{M}_1}-U_{\mathrm{N}_1}=\frac{\rho I}{2 \pi}\left(\frac{1}{A_1 M_1}-\frac{1}{B_1 M_1}-\frac{1}{A_1 N_1}+\frac{1}{B_1 N_1}\right) $

(4)

式中，A₁M₁、B₁M₁、A₁N₁、B₁N₁分别为电极A₁、B₁与M₁、N₁间的距离。

由式(3)可知：地铁杂散电流大小与电动列车取流大小、电动列车到直流牵引变电所的负极回流点的距离、轨道纵向电阻及轨道对大地的过渡电阻有关，在地电阻率仪完成一次电位差测量时间内，地铁杂散电流变化不大。考虑距地面线路6 km以外的电位大小时，可以将地铁运行时所产生的杂散电流看作为一点源。根据点电流源在半无限空间的计算公式，可求得地铁杂散电流I_d在测量极M₁、N₁处的电位差，公式如下

$ \Delta U_{1 \mathrm{~s}}=\frac{\rho I_{\mathrm{d}}}{2 \pi} \frac{1}{R_1}-\frac{\rho I_{\mathrm{d}}}{2 \pi} \frac{1}{R_2} $

(5)

式中，ΔU_ls表示杂散电流在两测量极处的电位差；R₁、R₂分别为塘沽台地电阻率南测量极M₁和北测量极N₁与地铁9号线的地表垂直距离，其中R₁ = 6.0 km，R₂ = 6.5 km。

根据式(4)、(5)，可分别求得地电阻率供电和地铁离散电流在南测量极和北测量极处的电位。为方便计算，地表电阻率统一取10 Ω·m。若地铁列车运行至距观测场地最近位置，并产生杂散电流，其对地电阻率观测影响的最大幅度可达16.1%(表 1)。

3.4 塘沽台自然电位估算杂散电流分析

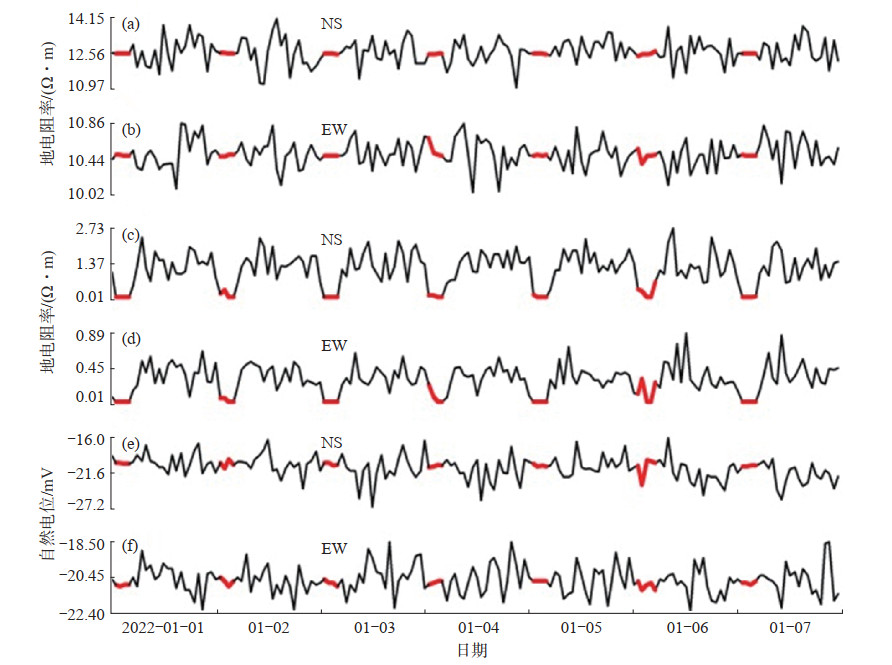
基于地铁运行的周期性特点，杂散电流干扰现象在地电观测中易于识别。如图 5，塘沽台地电阻率观测数据在每日地铁停运时段(每日1—4时)变化稳定(图中标红曲线)，而在地铁运行时段(每日5时—次日0时)则呈波动变化，干扰混杂其中。假设每日自然电位干扰完全来自地铁运行产生的杂散电流，将塘沽台自然电位按地铁停运和运行两时段进行分析，则有

$\Delta U_{\mathrm{sp}}^{\prime}=\Delta U_{\mathrm{sp}}+\Delta U_{1 \mathrm{~s}} $

(6)

式中，ΔU_sp为地铁停运时段的自然电位均值，$\Delta U_{\mathrm{sp}}^{\prime} $为地铁运行时段的自然电位均值，ΔU_ls为地铁离散电流在两测量极上所引起的电位差。

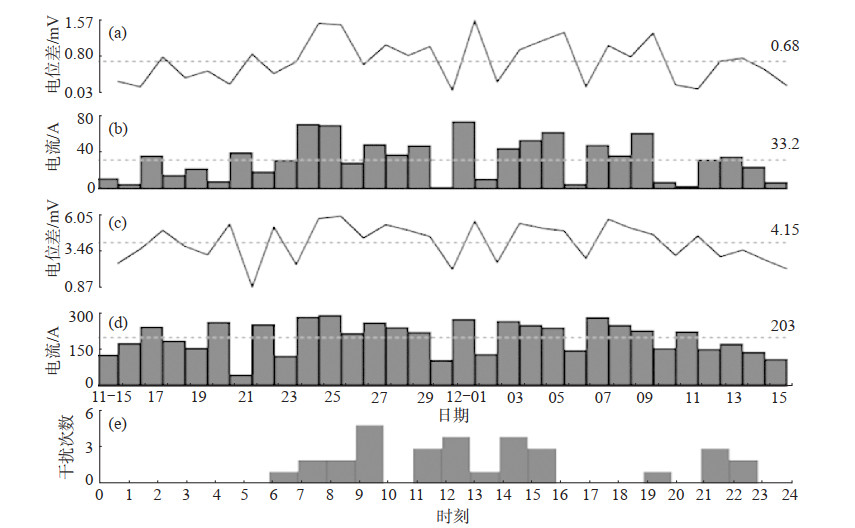
联立式(5)、(6)，可估算地铁杂散电流大小。选取塘沽台2021年11月15日至12月15日自然电位观测数据(此期间测区无灌溉作业、降水等影响因素)进行分析，发现杂散电流引起的电位差和估算的杂散电流并非恒定值，而是在一定范围内波动变化，结果见图 6。其中：杂散电流在南、北两测量极之间引起的电位差平均约为0.68 mV[图 6(a)]，估算的杂散电流日平均值约33.15 A[图 6(b)]；引起的自然电位最大日差值平均可达4.15 mV[图 6(c)]，估算的最强干扰日平均可达203.32 A[图 6(d)]。统计两时段自然电位相对变化最大时间，发现最强干扰主要出现在早高峰(7—10时)、上午收车(12—13时)、下午发车(15—16时)和夜间快车(22—23时)4个时段[图 6(e)]，此现象可能与最强干扰时段车次增加有关。如图 2(c)所示紧邻研究路段南侧的地铁9号线车务段，主要用于车辆停放和保养，最强干扰时段出现在地铁列车运行加密阶段，此时存在多次列车产生杂散电流并叠加的可能。

3.5 基于塘沽台地电阻率反算杂散电流

据地电阻率测量时序原理(图 7)，地电阻率观测剔除了自然电位变化的影响，但在测量人工电位时，地铁杂散电流仍有可能在两测量极之间产生电位差，使地电阻率测量结果受到干扰。选取塘沽台地电阻率2021年11月15日—12月15日数据进行分析，发现：每日1—4时，在地铁停运时段，地电阻率数据变化稳定[图 8(a)]，而在每日5时—次日0时，即在地铁运行时段，地电阻率数据则呈无规律的波动变化[图 8(b)]。为验证自然电位估算地铁杂散电流结果的准确性，用与自然电位同期的地电阻率观测数据进行反算验证。可基于式(4)求得M、N测量电极间的电位差，则地电阻率大小为

$ \rho=K \frac{\Delta U_{\mathrm{MN}}}{I} $

(7)

式中，$ K=2 \pi /(1 / A M-1 / B M-1 / A N+1 / B N)$。

据式(7)可知，在供电和测量装置不变前提下，地电阻率大小只与测量极之间的电位大小有关，则地铁运行时段地电阻率大小为

$\rho_{\mathrm{r}}=K \frac{\Delta U_{\mathrm{MN}}+\Delta U_{\mathrm{ls}}}{I} $

(8)

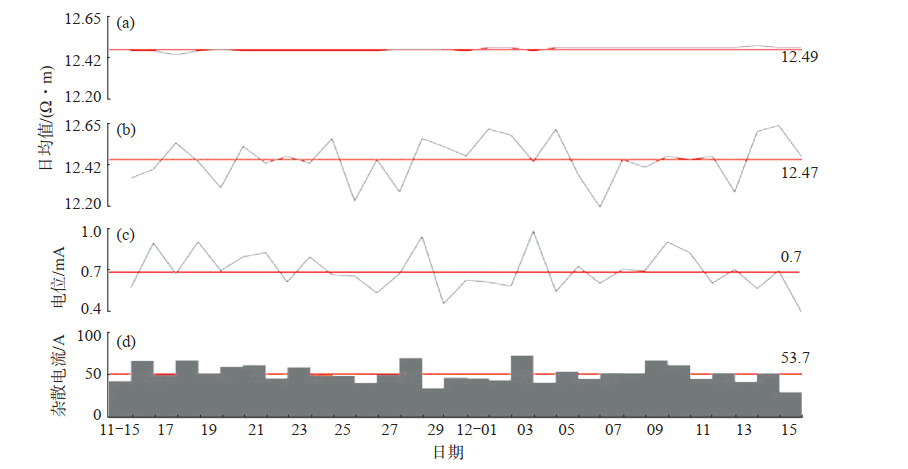
联立式(7)、式(8)，可利用两时段地电阻率数据求得ΔU_ls，由此反算得到杂散电流引起的电位变化平均约为0.70 mV[图 8(c)]，地铁杂散电流平均约为53.70 A[图 8(d)]。

将图 8(c)与图 6(a)进行对比，发现地电阻率数据反算结果略大于自然电位数据估算结果，应与自然电位和地电阻率测量时间不同有关，与塘沽台地电阻率观测环境干扰也有一定相关性。自然电位测量用时短，而地电阻率测量与多次正反向供电所测定的电位差有关，电位差测量次数越多，所需时间越长，在此期间，杂散电流已发生较大变化，有多次列车运行叠加的可能。

4 结论与讨论

经计算，地铁列车通过天津地铁9号线(距塘沽台最近)地面段时产生的最大杂散电流约为50 A；分段分析塘沽台自然电位数据，估算地铁杂散电流平均约为33.15 A，在两测量极之间引起的电位变化平均约为0.68 mV，使用地电阻率观测值反算的杂散电流平均约为53.7 A，电位变化平均约为0.70 mV。理论计算和实际观测均可证实，地铁运行会产生杂散电流，进而引起轨道周边自然电位发生变化。

通过对地电阻率观测每日最强干扰的统计，发现：在地铁运行早高峰(7—10时)、上午收车(12—13时)、下午发车(15—16时)和夜间快车(22—23时)4个时段的干扰最强，地铁杂散电流平均达203 A。如紧邻塘沽台的地铁Z2线路，其建成后，将对塘沽台地电阻率观测造成更大干扰。

如前所述，地铁杂散电流对地电阻率观测的干扰，与地铁轨道铺设方式、长度及其与地电观测装置相对距离等因素密切相关。当某一地震台站受到地铁运行干扰时，应首先掌握地铁线路的走向、铺设方式及运营时刻；在进行地电阻率观测前，利用同台自然电位数据进行快速估算，得到杂散电流水平；根据列车运营时刻，推算列车所处位置，利用“轨道—大地”模型计算地铁杂散电流的理论大小；基于点电流电位计算公式，求得杂散电流在测量极引起的电位变化。

估算所得杂散电流引起的电位平均变化略小于反算结果，其日最大值远大于理论计算结果。分析认为，可能有以下影响因素：①自然电位和地电阻率观测中，电位差观测次数和持续时间不同，其中自然电位正反向瞬时观测，而在地电阻率测量过程中，需多次供电并测量人工电位，所需时间较长，期间多班次地铁列车通过，有杂散电流叠加的可能；②理论计算模型较简单，仅考虑了单次列车的运行情况，然而在地铁运行高峰期，有多次地铁列车同时在分析路段运行的现象，此为实际观测结果出现远大于最大理论计算结果的主要原因；③塘沽地电阻率测区周边可能存在当前未知影响因素，在地电阻率观测时产生一定干扰。

中铁电气化勘测设计研究院肖立君在地铁牵引系统组成、天津地铁4号线车务段赵凯在地铁列车运营方式等方面提供了帮助，天津地震台刘双庆为论文制图提供了帮助，在此一并表示感谢。