0 引言

地震信号是地震监测预报、地层反演、地球勘探的基础。随着监测技术和通讯技术的进步，甚宽频带、大动态范围、高灵敏度地震计被广泛应用于地震台站，地震信号不可避免地受到周边环境影响，产出大量噪声信号。通过技术手段，采取有效措施对噪声干扰加以限制和消除，提高数据质量，是应用地震数据资料研究的基础。在长期地震监测与研究基础上（刘洋君等，2010），傅里叶变换、小波分析、Hilbert变换以及经验模态分解（EMD）信号等方法（黄艳林，2016；殷明等，2021）被广泛应用于地震数据分析和处理，有效进行噪声信号的改正和抑制。本文采用自适应噪声完备集合经验模态分解（Complete EEMD with Adaptive Noise，CEEMDAN）与小波包降噪结合的方法进行数据预处理，以期有效实现地震信号降噪。

1 基本原理 1.1 CEEMDAN方法原理

经验模态分解（Empirical Mode Decomposition，EMD）算法对于非线性、非稳定信号的分解具有独特优势，但分解过程存在模态混叠现象。为解决此问题，Torres等（2011）提出一种改进算法——CEEMDAN方法。该方法通过在EMD分解过程中自适应添加高斯白噪声，不仅克服了模态混叠问题，降低了集成次数，而且使得分解过程更加完整，几乎不存在重构误差，从而有效解决了模态混叠和端点效应。

CEEMDAN分解从2个方面解决了上述问题：①加入经EMD分解后含辅助噪声的IMF分量，而非将高斯白噪声信号直接添加在原始信号中；②EEMD分解和CEEMD分解是将经验模态分解后得到的模态分量进行总体平均，CEEMDAN分解则在得到第一阶IMF分量后进行总体平均计算，并对残余部分重复操作，从而有效解决白噪声由高频到低频的转移传递问题。

CEEMDAN算法原理如下：

（1）设定迭代次数为N，将N组成对正负高斯白噪声加入原始信号x(t)，得到N个新信号。第i次添加高斯白噪声后，新信号为

$ x_0^i(t)=x(t)+\varepsilon_0 w^i(t) $

(1)

式中：x(t)为原始信号；ε₀为噪声标准差；wⁱ为第i个满足标准正态分布的高斯白噪声。

（2）设E(*)为EMD分解数据序列，则通过i次分解可得到第i个IMF1分量，公式如下

$ E\left(x_0^i(t)\right)=\mathrm{IMF}_1^i(t)+r^i(t) $

(2)

式中：$ \operatorname{IMF}_1^i(t)$为第i个IMF1分量；rⁱ(t)为第i个残余分量。

（3）将分解所得N个IMF1分量求和，取平均值，得到最终IMF₁(t)，公式如下

$ \operatorname{IMF}_1(t)=\frac{1}{N} \sum\limits_{i=1}^N \operatorname{IMF}_1^i(t) $

(3)

（4）计算第1个残余分量r₁(t)：

$ r_1(t)=x(t)-\mathrm{IMF}_1(t) $

(4)

（5）在r₁(t)中加入步骤（1）中的N组成对正负高斯白噪声，采用EMD分解的辅助噪声，设E_h(*)为经EMD分解的第h个模态分量，则第i次添加辅助噪声后的新信号为

$ x_1^i(t)=r_1(t)+\varepsilon_0 E_1\left(w^i(t)\right) $

(5)

通过对$ x_1^i(t)$进行i次分解，得到第i个IMF2分量，分解结果为

$ E\left(x_1^i(t)\right)=\operatorname{IMF}_2^i(t)+r^i(t) $

(6)

对分解所得N个IMF₂求和，取平均值，得到IMF₂(t)，公式如下

$ \operatorname{IMF}_2(t)=\frac{1}{N} \sum\limits_{i=1}^N \operatorname{IMF}_2^i(t) $

(7)

计算第2个残余分量r₂(t)：

$ r_2(t)=r_1(t)-\mathrm{IMF}_2(t) $

(8)

（6）重复上述步骤，直至获得的残余分量不能继续进行EMD分解，算法结束。设此时IMF分量数量为k，则原始信号x(t)被分解为

$ x(t)=\sum\limits_{k=1}^K \operatorname{IMF}_k(t)+r_k(t) $

(9)

1.2 小波包去噪

相较于小波分析，小波包对信号的分析更加精细，时频平面划分更为细致，对信号高频部分的分辨率更高，而且可以根据信号特征选择最佳小波基，因此小波包分析应用更加广泛（高成，2007）。

结合地震信号非平稳随机性的特点，选择具有紧支性的db4小波基，将地震信号进行4层分解；根据基于无偏似然估计自适应阈值，以软阈值函数去噪，对数据进行小波包分解重构。

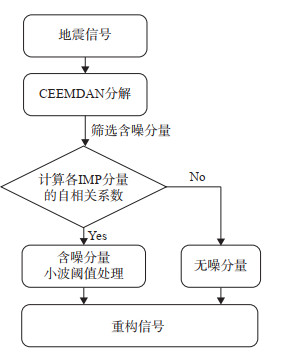
1.3 信号处理流程

采用CEEMDAN和小波包联合方法，对地震信号进行降噪处理，具体流程（图 1）如下：①采用CEEMDAN将地震信号分解为一系列IMF分量；②计算各IMF分量的自相关系数，以此来判断是否是含噪分量；③对含噪的高频IMF分量，利用小波包阈值方法进行降噪处理；④将各IMF分量组合重构，得到降噪信号。

2 仿真信号模拟 2.1 波形记录特征

为验证方法的可行性，设计一个仿真信号x(t)，采样点数N = 3 000，包含f₁ = 0.35 Hz和f₂ = 0.06 Hz两个频率成分，采样间隔0.01 s，n(t)为0.5倍信号振幅白噪声，信号仿真代码如下

x=2*cos(pi*f1*t)+3*cos(3*pi*f2*t)+0.15*exp(-15*t).*sin(20*pi*t);

nt=0.5*randn(1, N);

sig=x+nt;

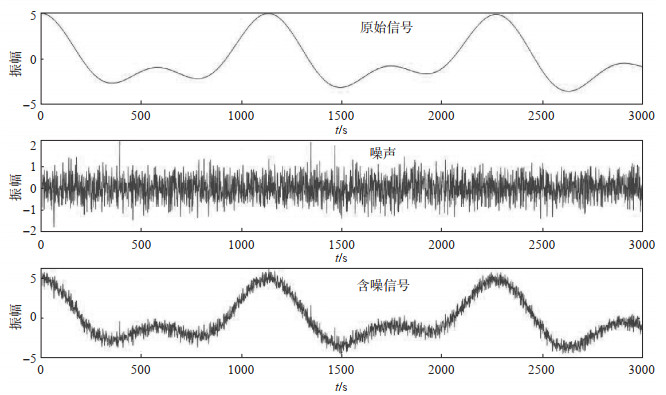
仿真信号波形见图 2。

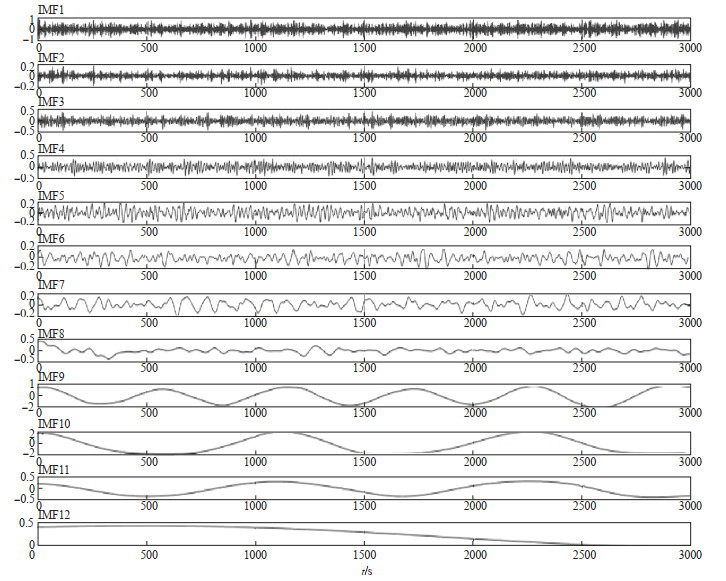
对含噪信号进行CEEMDAN分解，设计Nstd = 0.2，NR = 100，MaxIter = 500，结果见图 3。IMF1—4分量高频成分较多，IMF5—8分量高频成分逐渐减弱，IMF9—12分量长周期成分较多，可根据不同需要对各分量进行选择重构。

2.2 IMF分量选取

数据类型和需求不同，对于IMF分量的分析和处理方法也各不相同，主要有如下几种：①对IMF各分量均值是否显著区别于0进行t检验，区分高低频率成分，反应重大事件对信号的影响（齐绍洲等，2015）；②以熵值为标准，结合支持向量机SVM，提取特征指标，判断轴承、齿轮等机械故障（朱敏等，2020；蔡超志等，2022）；③计算IMF各分量与原始信号序列的Pearson相关系数、kendall相关系数、自相关系数，以区分含噪信号和有用信号，分别处理再重构，实现信号降噪的目的（马莹莹等，2022；谢锋云等，2023）。

本研究以地震信号为研究对象，以降低噪声、还原地震信号为主要目的，采用第三种方法，对各IMF分量进行自相关处理，判断其是否为含噪分量，将含噪IMF分量进行小波包降噪，与不含噪声的IMF分量进行重构。

噪声因其随机性特点，在不同时刻的信号关联性较差，其中自相关函数值在零点处最大，其他时段则迅速衰减。对于理想高斯白噪声，其归一化自相关函数值在零点处最大，在其他时段数值趋近于0。文中给出IMF1—12分量自相关系数，结果见图 4。

由图 4可见：①IMF1—8分量：除零点位置，其他时段频率迅速衰减，符合噪声随机分布的特点，判断为含噪分量；②IMF9—11分量：除零点位置，其他时段频率衰减缓慢，表现为影响分量成分和走向的信息成分，判断为无噪分量。

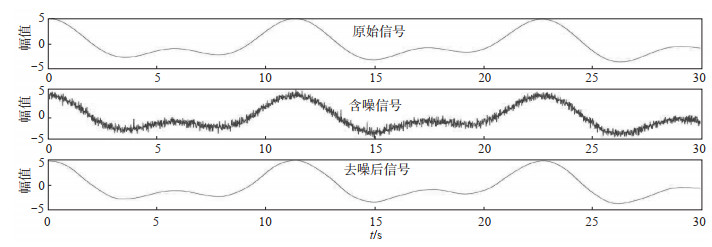
2.3 信号重构

对含噪分量IMF1—8进行小波包去噪，与其他无噪分量相加进行重构。如图 5所示，经过CEEMDAN和小波包处理，有效去除噪声干扰，提高了数据质量。

2.4 效果评价

将信噪比SNR、均方根误差RMSE作为检验指标，对去噪效果进行评价。

信噪比是科学研究和工程中所用的一种度量，用于比较所需信号的强度与背景噪声的强度。一般，信噪比越大，说明混在信号里的噪声越小，信号质量越高，否则相反。计算公式如下

$ \mathrm{SNR}=10 \text{lg} \frac{\sum\nolimits_{t=1}^T x_i^2}{\sum\nolimits_{t=1}^T\left(x_i-X_i\right)^2} $

(10)

均方根误差是均方误差的算术平方根，因均方误差的量纲与数据量纲不同，不能直观反映数据的离散程度，故在均方误差上开平方根，得到均方根误差，用来衡量观测值（真值）与预测值之间的偏差，其数值越小，表示测量精度越高。

$ \text { RMSE }=\sqrt{\frac{1}{N} \sum\nolimits_{t=1}^N\left(\text{observed}_t-\text{predicted}_t\right)^2} $

(11)

分别采用CEEMDAN、小波包软阈值和二者联合方法进行地震数据拟合，评价效果见表 1，可见采用联合方法进行数据拟合，优于单一方法的拟合结果，其在对信号去噪的同时，尽可能多的保留原数据中的信息，可为数据后续分析和使用提供参考。

3 地震资料处理

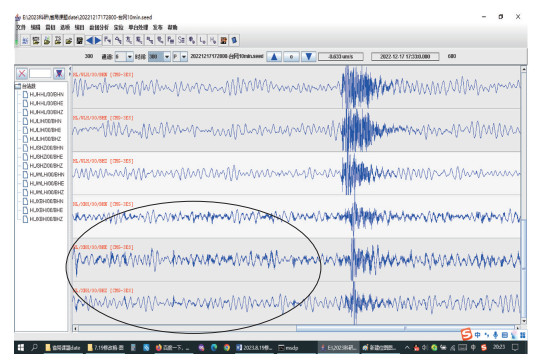
截取镜泊湖火山台网2022年12月某时段监测记录原始波形，见图 6，图中空心椭圆所示为小北湖子台记录，采用CEEMDAN和小波包方法，对该子台数据进行去噪处理。

小北湖子台临近乡间小路，白天有农用车辆经过，波形显示，监测记录受到高频干扰，噪声混杂其中，数据质量不高。对该子台数据进行去除趋势项处理，消除漂移对数据的影响。采用CEEMDAN方法将数据分解为IMF1—17分量，计算自相关系数可知，IMF1—8分量为含噪分量，经小波包阈值方法降噪后与其他分量重构。

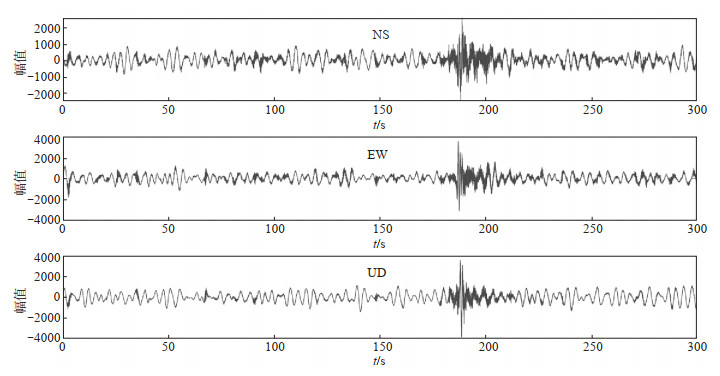
结果如图 7所示，通过对小北湖子台数据的降噪处理，可见剔除高频干扰的同时，原有背景信息得以保留，有助于数据的分析应用和后续研究的开展，提高了数据的识别度和准确性。

4 结论

自适应噪声完备集合经验模态分解CEEMDAN方法是一种新型信号分解算法，可较好地解决经验模态分解存在的模态混叠现象，对分解后的IMF分量加以分析甄别，有选择地进行信号处理和重构，满足多种频率成分分析的需要，对于地震数据处理和信息深度挖掘均能达到较好的效果。

简单地舍弃高频IMF分量会损失部分高频信号，通过对各IMF分量自相关系数的计算，可比较客观地筛选含噪分量，通过小波包阈值降噪处理实现信号重构，有效保留了高频成分和弱信号部分，达到了预期效果。