0 引言

中国地电台网观测系统主要由“九五” “十五”项目升级改造而来，距今已有10多年，地电仪器、避雷装置、外线路等老化现象较为严重，一些台站需要进行技术升级和更新。而且，随着我国经济建设的快速发展，部分地电观测场地环境因地铁、铁路、轻轨、高速公路等影响受到不同程度的破坏，导致地电阻率数据出现“超差”现象，严重影响地电观测数据的质量和连续性。

地电台站在完成日常观测、资料预处理、跟踪分析等工作的同时，若当地电阻率数据出现超差现象，需要落实数据变异原因。目前台站多采用替换法来排查该超差现象，即更换主机、稳流源、避雷装置、电极、闸刀等，并对观测场地环境进行巡检。然而，地电阻率的超差现象随机性较强，不易捕捉，且因涉及面广，加之传统排查方法周期较长、效率较低、针对性差等缺点，使得排查难度加大。为了能够快速处理地电阻率超差现象，本研究利用电压采集仪，对地电观测系统相关测道2个测量极间的供电电位差秒数据进行实时采集，通过分析供电波形形态特征，识别造成超差现象的原因，从而准确判断是观测系统还是观测场地周边其他干扰所致。该方法的使用缩短了超差现象的排查周期，提高了检测效率。

1 地电阻率超差现象判定原理

基于地电阻率、均方差、相对均方根误差计算公式，了解地电阻率观测系统供电电压波形变化过程，有利于快速分析并判断地电阻率超差成因。

地电阻率ρ_s计算公式如下

$ \rho_{\mathrm{s}}=K \Delta V / I $

(1)

式中，K为装置系数为常数；I为供电电流，一般固定在2 A左右；ΔV为供电电位差。由式（1）可知，装置系统K、供电电流I不变，ΔV为人工供电电位差，可通过测量得到，且其与地电阻率值成正比。而ΔV =（ΔV + V_sp）-V_sp，测量极之间的电位差V_sp和供电电位差ΔV出现变化都会引起电阻率的变化，可见二者的稳定性对地电阻率测量精度起到决定作用。

每小时地电阻率观测值可视为n次地电阻率测值的平均值，公式如下

$ \bar{\rho}_{\mathrm{s}}=\frac{\sum\nolimits_{i=1}^n \rho_{\mathrm{s}}(i)}{n} $

(2)

式中，ρ_s为地电阻率平均值；ρ_s(i)为地电阻率第i次测值；n一般选5—10次。

视电阻率观测精度是所测视电阻率准确程度的度量，由系统误差和偶然误差2部分组成（中国地震局，2001）。系统误差可以采取措施加以克服，而偶然误差是多种因素的综合作用，使得观测值在均值附近波动，其大小用均方差来表示。也就是说，均方差用于衡量随机变量或1组数据的离散程度。每组多次观测值的均方根误差计算公式如下

$ \sigma_{n-1}=\sqrt{\frac{\sum\nolimits_{i=1}^n\left(\rho_{\mathrm{s} i}-\overline{\rho_{\mathrm{s}}}\right)^2}{n-1}} $

(3)

式中，n为观测次数；ρ_si为第i次观测值；ρ_s为n个ρ_si的算术平均值。ρ_si值离散度越大，均方差越大，说明测量所得供电电位差变化大，不稳定。σ_n-1值的大小反映了多个ρ_si观测值的离散度及观测系统稳定性和环境影响大小（何世根，2000）。在地电阻率观测中，导致σ_n-1值变大的原因主要有主机故障、稳流电源故障、外线漏电、电极以及环境干扰等（张国清，2009）。

地电阻率相对均方根误差K_σ计算公式如下

$ K_\sigma=\frac{\sigma_{n-1}}{\bar{\rho}_{\mathrm{s}}} \times 100 \% $

(4)

若K_σ≥3%，在ZD8BI、ZD8M型地电仪器显示器及网页上则显示超差现象，说明该组地电阻率值误差大，观测结果不可靠，观测仪器将自动舍去该数值。

观测过程中，对地电阻率仪器多次正反向供电，以测量不同时段的人工电位差，计算相应时段的地电阻率值，了解人工电位差变化特征。

若自然电位差平直稳定，说明地电观测系统和观测环境正常；反之，观测环境受到干扰或观测系统不稳定就会出现超差现象。人工供电电位差误差越小，则均方差越小，表明观测值精度越高。如果出现超差现象，说明地电观测环境存在干扰或观测系统不稳定，如主机内部电路故障、外线路破损漏电、电极故障、电极附近有环境干扰等。

2 地电阻率超差现象识别

在地电仪器观测中，经常发现地电数据在仪器显示屏显示“超差”（图 1）。基于M、N测量电极间自然电位差时序变化特征可知，若测区观测环境存在干扰或观测系统不稳定，地电阻率测值会出现超差现象。以洛阳地震台（下文简称洛阳台）2020—2021年地电阻率出现的超差现象为例，从观测环境和观测系统进行系统分析。

2.1 地电外线路断线引起的超差识别

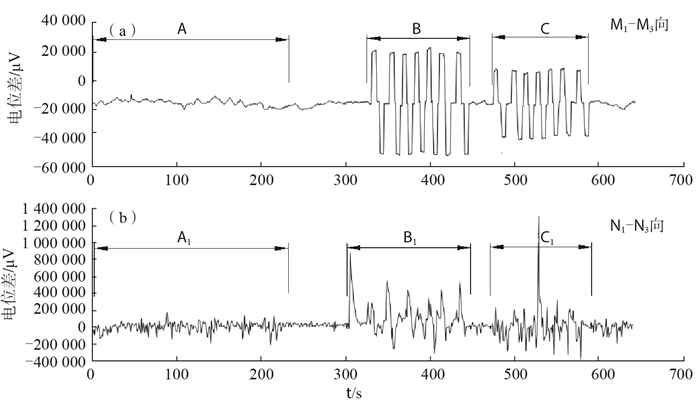
洛阳台地电阻率NS向分量于2020年10月31日14时出现超差现象，自然电位同时出现异常跳动（图 1）。为判别导致超差现象的原因，采用连接法，将电压采集仪（洛阳台研制）的第1、2测道接入地电观测系统测量极M₁、N₁、M₃、N₃，其中，第1测道接M₁、M₃地电外线路，第2测道接N₁、N₃地电外线路（图 2），以快速判断M₁、N₁电极是否出现问题，由此得到15时地电阻率供电波形（图 3）。由图 3可见，与B、C段相比，B₁、C₁段波形严重畸变，可见超差现象依然存在。

将M₁—M₃、N₁—N₃测量极电位差曲线进行对比，认为N₁外线路可能存在故障，主要体现在：A段自然电位差正常变化，A₁段自然电位差为未观测时数据已出现干扰；B₁、C₁段供电波形不稳定，B、C段供电波形相对清晰，说明仪器工作正常，表明地电阻率超差由N₁或N₃外线路故障造成，由于地电观测仪器观测值EW向自然位和电阻率正常，因此排除M₁故障，最终判断为N₁外线路断线造成超差现象。使用绝缘摇表对该线路进行绝缘检查，发现电阻大于500 MΩ，场地线路检查发现，距N₁测量极30 m处地电外线被树压断，处理后恢复正常。

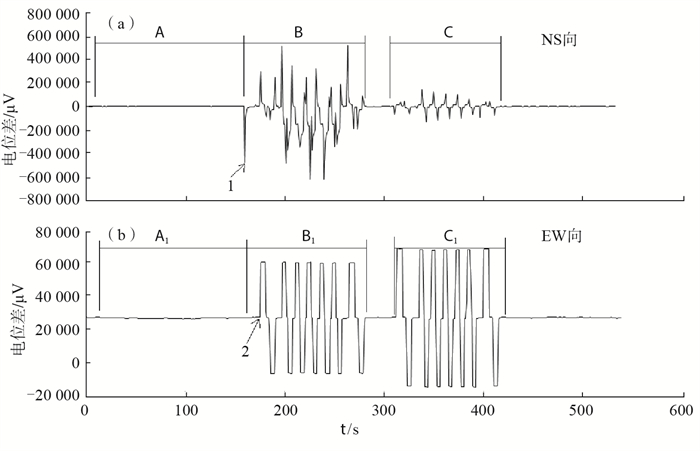
洛阳市地铁修建初期对地电阻率观测的影响较大。2020年12月地铁1号线开通，进行低、中、高密度车辆通电试运行。12月下旬中、高密度试车，31日洛阳台地电阻率NS向数据连续4 h出现超差，此后1个月内经常出现连续几小时的超差现象，初步认为由地铁试运行流散电流所致。且随着时间的延续，发现该超差现象只在NS向地电阻率观测数据中出现，2021年1月22日超差持续6 h，于20时接入电压采集仪，记录波形见图 4。

由图 4（a）可见，地电阻率数据出现超差时，NS向供电波形B、C段严重畸形，而EW向B₁、C₁段供电波形正常。若为地铁干扰，则2个方向将受到同步影响（图 5），表明NS向地电阻率数据超差非地铁引起，可能为NS向观测系统或外环境有问题所致。由图 4（b）可见，B₁段供电波形正常，说明稳流电源和供电线路正常，问题出现在M₁、N₁电极NS向装置系统的测量线路上。图 4（a）中曲线显示，A段自然电位差正常，说明M₁、N₁电极NS向测量线路、外环境正常。通过以上分析和逐一排除法，判断数据超差由地电阻率NS向测量系统出现问题所致。图 4（a）中位置1向下尖峰比图 4（b）中位置2的供电起始时间提前15 s，而前者对应仪器内部AD转换板上NS向继电器吸合时自然电位差测量时间，该继电器的作用是测量自然电位差和人工供电电压，若其出现故障，易导致数据超差。基于以上分析，判断测量系统AD板上继电器故障造成超差。更换继电器后观测数据恢复正常，再无连续几小时的超差现象出现。

2021年2月3日14时，洛阳台地电阻率NS向数据出现超差，而该分向测量极波形正常[图 5（a）]。由图 5（a）B段可见，相应位置人工供电电位高低不一，人工供电电位差变化较大，均方根误差变大，相对均方根误差K_σ＞3%，这使得NS向地电阻率数据出现超差。图 5（a）中曲线B段显示，供电波形高点电压跳动约5 000 μV，而EW向B₁段约3 000 μV[图 5（b）]，相对稳定，均方根误差较小，不会造成该分向地电阻率数据出现超差现象，说明地电观测系统、外环境基本正常。洛阳轨道交通1号线呈EW向展布，距洛阳台地电阻率观测场地约13 km，对EW向地电阻率数据干扰小，而2号线呈NS向展布，距该台地电阻率观测场地约5 km，NS向地电阻率数据出现的干扰幅度较大，确定为地铁干扰。节假日期间地铁车次数成倍增加，使得B段、B₁段供电波形高低点电压上下跳动幅度大于10 000 μV，导致地电阻率观测数据也会出现超差。

3 结束语

在日益复杂的电磁干扰环境下，地电阻率观测面临数据干扰排查的较大考验。由于地电阻率观测仪器为整点值观测，在出现数据超差现象时，较难判断具体故障原因或干扰源位置。通过地电仪器供电过程中电位差波形图，可清晰观察仪器观测过程，分析供电波形前自然电位差变化和供电电位差波形异常变化的特征，最终确定数据超差原因，并可通过上述2条测量曲线相互对比论证，快速、准确地判断故障位置，这为今后地电阻率观测数据的异常排查提供了一种新方法。