2) 中国内蒙古自治区 026000 锡林浩特地震监测中心站
2) Xilinhot Earthquake Monitoring Center Station, Inner Mongolia Autonomous Region 026000, China
震级是表示地震本身大小的一个量,是地震的基本参数之一(刘瑞丰等,2014)。根据震级可以近似地得到其他震源参数;对于浅源地震,震级越大,地震所造成的灾害越严重,所以震级是地震应急、地震救援、灾害损失评估等工作中的重要参数(刘瑞丰等,2014)。因此,准确测定震级是一项意义重大的基础性工作(刘瑞丰等,2014)。在台站日常数据处理中发现,台站测定的面波震级与中国地震台网中心发布的震级之间存在一定的偏差。台基、震源、地质构造等差异会造成震级的测定存在偏差(刘瑞丰等,2011;刘芳等,2016;李晓东等,2017;郭延杰等,2020)。因此,选取全球734个MS≥5.5且波形清晰的地震事件,对其进行分析,探究导致海拉尔地震台面波震级偏差的原因,以期为海拉尔地震台准确测定震级提供参考依据,进一步提高单台地震定位的精度。
1 台站信息与资料选取海拉尔地震台位于内蒙古自治区东部呼伦贝尔市海拉尔区的西北郊,地处海拉尔盆地与大兴安岭接壤地带。为了加强对德尔布干断裂带、海拉尔河断陷盆地、嫩江断裂带地震活动的监测,弥补我国东北西部地区地震台网监测能力的不足,1974年开始建设海拉尔地震台,1978年1月起该台正式投入地震观测。岩性属中生代侏罗纪安山岩,台站代码为HLR,属国家基本台。台站使用BBVS-120型宽频带三分项地震计和EDAS-24IP型地震数据通信采集器。地震计安装在观测山洞中,山洞总长85 m,面积242.5 m2,覆盖层厚23 m。选取海拉尔地震台2017年8月1日至2021年12月31日记录到的全球MS≥5.5且波形清晰的734个地震事件。
2 方法 2.1 面波的测定海拉尔地震台使用MSDP地震分析处理软件,将数字地震波形仿真成中长周期和长周期,依次量取NS向、EW向、垂直向最大振幅及对应周期,得到面波震级(赵瑞等,2017)。依据GB 17740—2017《地震震级的规定》(刘瑞丰等,2017)可知面波震级计算方法如下:
(1) 使用基式(SK)中长周期地震仪记录面波质点运动最大速度,计算公式为
| $ M_{\mathrm{S}}=\lg \left(\frac{A}{T}\right)_{\max }+1.66 \lg \varDelta+3.5 \quad\left(1^{\circ}<\varDelta<130^{\circ}\right) $ | (1) |
式中,A为两水平向面波地动位移的矢量和;T为相应的周期;Δ为震中距。
(2) 使用763型长周期地震仪记录,以垂向瑞利波质点运动最大速度测定震级,计算公式为
| $ M_{\mathrm{S} 7}=\lg \left(\frac{A}{T}\right)_{\max }+\sigma_{763}(\varDelta) \quad\left(3^{\circ}<\varDelta<177^{\circ} ; T>6 \mathrm{~s}\right) $ | (2) |
式中,A为垂直向瑞利波质点运动最大速度对应的位移值;T为相应的周期;Δ为震中距;σ763(Δ)为量规函数。
使用763型长周期地震仪记录确定的面波震级MS7与世界标准台网WWSSN的震级结果基本一致(刘瑞丰等,2006),故使用MS7震级数据。下文直接用MS表示。
2.2 偏差分析对选取的734个地震事件进行处理,将台站测定的面波震级与中国地震台网中心正式目录的面波震级进行偏差分析。
对每一个地震事件计算面波震级偏差
| $ \Delta M_{\mathrm{S} i}=M_{\mathrm{S}_i(\mathrm{HLR})}-M_{\mathrm{S} i(\mathrm{CENC})} \quad(i=1, 2, 3, \cdots, 734) $ | (3) |
取面波震级平均偏差
| $ \bar{M}_{\mathrm{S}}=\frac{1}{n} \sum\limits_{i=1}^n \Delta M_{\mathrm{S} i} \quad(1 \leqslant n \leqslant 734) $ | (4) |
再取面波震级标准偏差
| $ s=\sqrt{\frac{\sum\limits_{i=1}^n\left(\bar{M}_{\mathrm{S}}-\Delta M_{\mathrm{S} i}\right)^2}{n-1}} \quad(1 \leqslant n \leqslant 734) $ | (5) |
式中,MSi(CENC)为中国地震台网中心正式目录中第i个地震事件的面波震级;MSi(HLR)为海拉尔地震台测定的第i个地震事件的面波震级;ΔMSi为第i个地震事件的面波震级偏差;
利用式(3)—(5)计算得到,面波震级平均偏差为-0.404 9,面波震级标准偏差为-0.377 7,说明MS(HLR)与MS(CENC)之间存在一定的偏差且偏差较大,MS(HLR)较MS(CENC)偏小0.4级。
统计不同震级偏差与对应出现的地震事件次数之间的关系,列出震级偏差与频次、平均震源深度表(表 1)。
| 表 1 震级偏差与频次、平均震源深度 Table 1 Statistical table of magnitude deviation, frequency and average focal depth |
根据震级的不同,将734个地震事件划分为5.5—5.9级、6.0—6.9级、7.0—7.9级、8.0级以上等4种类型,分别统计每种类型的地震数并计算平均震级偏差(表 2)。由表 2可知,海拉尔地震台测定的面波震级较中国地震台网中心正式目录的面波震级均偏小,5.5—5.9级地震面波震级偏小约0.4级,6.0—7.9级地震偏小约0.3级,8.0级以上地震偏小约0.2级。
| 表 2 不同震级地震的面波震级平均偏差情况 Table 2 Deviation of surface wave magnitude for different magnitudes |
震源深度小于60 km的地震被称为浅源地震,全球有80%左右的天然地震是浅源地震;震源深度大于300 km的地震被称为深源地震;震源深度为60—300 km的地震被称为中深源地震(中国地震局监测预报司,2017)。
根据震级偏差的不同,对734个地震事件分别计算相同震级偏差下地震事件的平均震源深度(表 1)。另根据震源深度的不同,将734个地震事件分为h>300 km、60 km≤h≤300 km、h<60 km等3种类型,分别统计每种类型的地震数并计算平均震级偏差(表 3)。结合表 1、3可知,震源越深,海拉尔地震台测定的面波震级与中国地震台网中心正式目录的面波震级偏差越大,且均偏小。当震级偏差绝对值大于0.7时,对应的地震事件平均震源深度也基本大于60 km。在本文所研究的地震事件中,有83.79%为浅源地震,且面波震级平均偏差为-0.3级。
| 表 3 不同震源深度地震的面波震级平均偏差 Table 3 Deviation of surface wave magnitude at different focal depths |
根据震中距的不同,将734个地震事件划分为Δ<10°、10°≤Δ<30°、30°≤Δ<60°、60°≤Δ<105°、105°≤Δ<130°、Δ≥130°等6种类型,分别统计每种类型地震数并计算平均震级偏差(表 4)。已知Δ<10°的地震为近震,近震震级通常不用面波震级MS来描述,因此对2个Δ<10°的地震事件不作分析;Δ≥105°的地震为极远震,但式(1)适用范围为1°<Δ<130°,式(2)适用范围为3°<Δ<177°,因此在根据震中距划分地震事件类型时,将极远震分成105°≤Δ<130°、Δ≥130°等2种类型进行讨论。由表 4可知,海拉尔地震台测定的面波震级较中国地震台网中心正式目录的面波震级均偏小。大部分地震事件震中距为[30°,60°)、[60°,105°)两个区间,个数分别为252、235,且地震面波震级均偏小约0.4级;震中距为[10,30)、[105,130)两个区间的地震面波震级均偏小约0.3级;而极远震中Δ≥130的地震面波震级偏小约0.4级。
| 表 4 不同震中距的面波震级偏差情况 Table 4 Deviation of surface wave magnitude with different epicenter distances |
以海拉尔地震台为坐标原点,选取正北、正东方向为坐标轴,将所选择的734个地震事件根据方位角的不同,划分在东北、东南、西南、西北等4个象限内,分别统计每个象限的地震数并计算每个象限地震的平均震级偏差(表 5)。由表 5可知,海拉尔地震台测定的面波震级与中国地震台网中心正式目录的面波震级相比偏小。超50%的地震事件发生在海拉尔地震台的东南方向,该方位地震的震级偏差最大,为-0.47级;其他方位地震的震级偏差绝对值为0.2—0.3。
| 表 5 不同方位的面波震级偏差情况 Table 5 Deviation of surface wave magnitude in different directions |
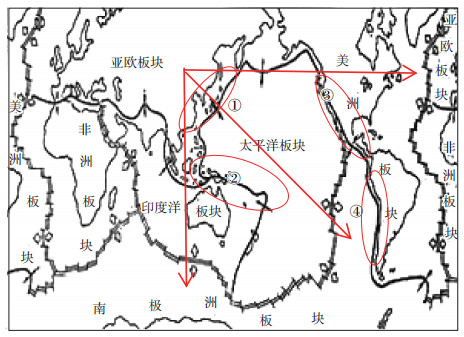
由表 5可知,海拉尔地震台东南方向的地震事件占比较高且震级偏差较大,因此选取东南方向地震发生频次较高的地区进行进一步分析(表 6),并利用板块分布图对海拉尔地震台东南方向地震的震级偏差与地区间的关系进行说明(图 1)。
| 表 6 东南方向不同地区的面波震级偏差情况 Table 6 Deviation of surface wave magnitude in different regions in southeast direction |
|
图 1 海拉尔地震台东南方向地震震级偏差与地区间关系示意图 Fig.1 Map of the southeast magnitude deviation and its regional relationship at the Hailar District seismic station |
结合表 6与图 1可知,在海拉尔地震台东南方向内发生的地震事件中,位于东偏南45°内的地区,震中距为30°≤Δ<130°的地震震级偏差较小,如美国加利福尼亚州及其附近地区和墨西哥及其附近地区(图中③区),约为-0.28级;震中距Δ≥130°的地震震级偏差与平均偏差相近,如智利及其附近地区(图中④区),约为-0.46级。而位于南偏东45°内的地区,震中距为30°≤Δ<130°的地震震级偏差较大,如瓦努阿图群岛、所罗门群岛及其附近地区与印度尼西亚及其附近地区(图中②区)约为-0.61级。对于震中距为20°左右的地震震级偏差较小,如日本及其附近地区(图中①区),约为-0.28级。
5 面波震级MS与矩震级MW间偏差分析由不同震级标度测定的是特定频段的地震波振幅,当震级大到一定级别时,测定的最大振幅不再增加,这使测得的地震震级不再随地震的增大而增大,该现象被称为震级饱和(陈运泰等,2018)。为了解决此问题,基于地震矩与面波震级间的关系,Kanamori(1977)提出矩震级的概念,Hanks等(1979)给出矩震级定义式
| $ M_{\mathrm{W}}=\frac{2}{3} \lg M_0-10.7 $ | (6) |
式中,M0为地震矩,单位dyne·cm(沙海军等,2018)。
现将海拉尔地震台测定的面波震级MS(HLR)与美国地质调查局(USGS)官网发布的地震矩震级MW(USGS)进行偏差分析。计算MS(HLR) -MW(USGS),得到震级的平均偏差为-0.429 2,震级偏差的标准差为s′ = 0.387 1。结合平均偏差与标准偏差,可以说明MS(HLR)与MW(USGS)之间也存在一定的偏差且偏差较大,MS(HLR) 较MW(USGS)相比偏小0.43级。
同时,对台网中心正式目录的面波震级MS(CENC)与美国地质勘探局官网发布的地震矩震级MW(USGS)之间相比较,计算MS(CENC) - MW(USGS),得到震级平均偏差为-0.028 25。可以看出二者间差距较小,基本一致。而台站测定的面波震级分别与台网中心正式目录的面波震级和美国地质勘探局官网发布的地震矩震级相比,平均偏差均较大,分别为-0.404 9、-0.429 2;标准差分别为-0.377 7、-0.387 1。故海拉尔地震台面波震级偏差较大,较MS(CENC)与MW(USGS)均偏小0.4级左右。
6 结论(1) 海拉尔地震台测定的地震面波震级偏差较大,比中国地震台网中心正式目录的面波震级平均小0.4级,比美国地质调查局官网发布的矩震级平均小0.43级。
(2) 将海拉尔地震台测定的面波震级与中国地震台网中心正式目录的面波震级相比,通过偏差分析计算可知:①震级与面波震级偏差之间为反相关,即震级越大,偏差越小。8.0级以上的地震震级偏差为-0.20级,而大部分地震分布在5.5—6.9级,该范围内震级偏差为-0.40级,与海拉尔地震台测定的面波震级平均偏差相符。②震源深度与面波震级偏差之间为正相关,即震源越深,偏差越大。而大部分地震为浅源地震,偏差为-0.30级。③震中距与面波震级偏差之间存在一定的关系,即震中距范围在[10°,30°)、[105°,130°)间的地震面波震级偏差较小,为-0.30级,在其他范围内偏差为-0.40级,与海拉尔地震台测定的面波震级平均偏差相符。④方位角与面波震级偏差之间存在一定的关系,即方位角位于东南方向时,面波震级偏差最大,为-0.47级;方位角位于西北方向时,面波震级偏差最小,为-0.20级。⑤对发生在海拉尔地震台东南方向的地震事件按地区分析时发现,对于发生在日本地区、美国加州地区和墨西哥地区的地震,面波震级偏差较小,为-0.30级;而对于发生在澳大利亚板块与太平洋板块碰撞地带的地震,如瓦努阿图群岛、所罗门群岛及其附近地区与印度尼西亚及其附近地区,面波震级偏差较大,为-0.61级。
陈运泰, 刘瑞丰. 矩震级及其计算[J]. 地震地磁观测与研究, 2018, 39(2): 1-9. |
郭延杰, 包莹, 齐彬彬, 等. 赤峰中心地震台面波震级偏差分析[J]. 地震地磁观测与研究, 2020, 41(2): 57-61. |
李晓东, 李姗姗, 周远新, 等. 库尔勒国家数字地震台近震震级偏差分析[J]. 地震地磁观测与研究, 2017, 38(4): 45-48. |
刘芳, 刘瑞丰, 张帆, 等. 内蒙古东部地区面波震级与近震震级转换关系[J]. 地震地磁观测与研究, 2016, 37(5): 1-9. |
刘瑞丰, 陈运泰, Bormann P, 等. 中国地震台网与美国地震台网测定震级的对比(Ⅱ)——面波震级[J]. 地震学报, 2006, 28(1): 1-7. |
刘瑞丰, 任克新, 张立文, 等. 利用宽频带数字地震资料测定地震震级的方法研究[J]. 地震地磁观测与研究, 2011, 32(3): 1-8. |
刘瑞丰, 陈运泰, 任枭, 等. 震级的测定[M]. 北京: 地震出版社, 2014: 1-48.
|
刘瑞丰, 王丽艳, 袁乃荣, 等. 《地震震级的规定》(GB 17740-2017)宣贯教材[M]. 北京: 地震出版社, 2017: 1-9.
|
沙海军, 吕悦军. 中国地震台网面波震级与矩震级统计关系[J]. 地震地磁观测与研究, 2018, 39(6): 31-36. |
赵瑞, 李俊超, 万禹, 等. 钟祥地震台面波震级测定[J]. 地震地磁观测与研究, 2017, 38(4): 49-52. |
中国地震局监测预报司. 测震学原理与方法[M]. 北京: 地震出版社, 2017: 1-54.
|
Hanks T C, Kanamori H. A moment magnitude scale[J]. Journal of Geophysical Research: Solid Earth, 1979, 84(B5): 2 348-2 350. |
Kanamori H. The energy release in great earthquakes[J]. Journal of Geophysical Research, 1977, 82(20): 2 981-2 987. |
 2023, Vol. 44
2023, Vol. 44


