现代地震学研究是以准确的三分量宽频带观测为基础的,地震记录中地震事件的到时、振幅、质点运动轨迹都是地震学研究的重要组成部分。在有关剪切波分裂、震源机制反演、震源破裂过程反演、接收函数、面波、自由震荡等研究中,研究人员通常将水平分量的地震记录旋转至径向、切向来分离P-SV、SH波。极性旋转的准确性取决于地震计北南(NS)分量方向与地理N向之间是否存在偏转角度,偏转角度越大,对后续研究结果的准确性和可靠性影响越大(陈继锋等,2016;魏贵春等,2017;王婷等,2020;陈家樑等,2021)。
地震计方位偏差主要来自2个方面,一是地震计的生产制造过程;二是地震计的安装过程。现代宽频带地震计制造采用了一体化的结构设计,即三分量的传感器保持正交,三轴正交性偏差均小于0.9°(Ringler et al,2013;中国地震局,2020)。因此,地震计方位偏差主要来自安装过程,其安装可分为确定正N方向、勾画参考线、布设地震计等3个步骤。理论上,最精确的寻北方法是利用寻北仪(陀螺仪)确定地理N向,利用激光仪等将地震计的NS方向与地理N向对齐。然而实际工作中,安装条件、磁性环境等都可能造成仪器安装方位偏差(Niu et al,2011)。
目前,国内外已经发展出一系列方法估计并校正地震计的方位角偏差,主要分为4类:①根据长周期瑞雷波的极性评估台站仪器的方位角偏差(Laske,1995;Selby,2001;Baker et al,2004;Stachnik et al,2012;Rueda et al,2015;Doran et al,2017);②噪声互相关方法(Zha et al,2013);③理论面波与观测面波互相关方法(Ekström et al,2008);④根据远场P波的质点运动轨迹分析台站仪器的方位角偏差(Schulte-Pelkum et al,2001;Niu et al,2011)。Niu等(2011)利用P波质点运动轨迹方法估算了中国数字地震台网地震计方位角偏转情况,发现约有1/3的台站存在仪器方位角偏差、极性反转等问题。2012年11月起,各省(市、自治区)地震局对其辖区内的固定台站陆续开展了方位角校正工作,地震计方位角偏转问题得到了有效改善。
中国西北、西南区域是我国地震活动较频繁的地区,全国约77%的破坏性地震在此发生,青藏高原、南北地震带、天山造山带都是目前地震学研究的重点区域(陈兵等,2003;许英才等,2018;李伟等,2019)。西北、西南地区的部分区域台站布设难度大,分布较稀疏,地震数据资料极为宝贵。为更好地服务于地震科学研究工作,本文利用P波质点运动轨迹分析方法计算2019—2020年西北、西南地区211个地震台站地震计方位角偏差,给出部分台站方位角随时间的变化,并结合地震台网运维日志进行佐证,以确保方位角偏差值的可靠性,方便科研人员对测震数据的使用。
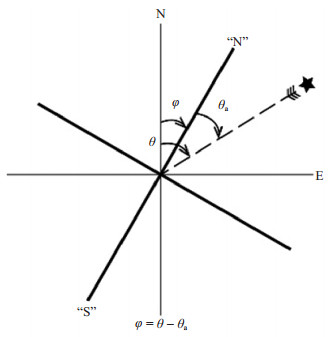
1 计算方法在层状各向同性介质中,P波的偏振方向是线性的。P波质点运动轨迹与地震波的传播方向一致,位于震源与接收台站的垂直平面内,因此其在水平面上的投影与台站后方位角方向平行(图 1)。此时,P波的能量分布在垂向(BHZ)、径向(BHR)分量,切向(BHT)上无能量。
|
图 1 地震计方位角计算原理示意图 NS方向与地理N之间的方位角偏差用φ表示,顺时针为正,φ可由台站后方位角θ与P波质点运动求出的后方位角θa之间的几何关系计算得到 Fig.1 A schematic plot of station sensor orientation |
如果某个台站地震计的NS方向与地理N向间存在偏差φ,根据台站和震中的经纬度可以计算出台站的后方位角θ,θa则为视后方位角,台站的方位角偏差φ = θ-θa。对于一条波形记录,可以利用初至P波三分量记录构建协方差矩阵,通过求解矩阵的特征值、特征向量来获得P波的极化方向(Jurkevics,1988)。由于地震仪3个分量相互正交,可以将协方差矩阵进一步简化为2个水平分量的协方差矩阵C,可表示为
| $ \boldsymbol{C}=\left(\begin{array}{ll} C_{\mathrm{NN}} & C_{\mathrm{NE}} \\ C_{\mathrm{NE}} & C_{\mathrm{EE}} \end{array}\right), C_{i j}=\int_{t_1}^{t_2} \mu_i(t) \mu_j(t) \mathrm{d} t \quad(i, j=\mathrm{N}, \mathrm{E}) $ | (1) |
其中,t1、t2为选取的P波时间窗;μ(t)表示地震记录。该矩阵的特征值为
| $ \lambda=\frac{1}{2}\left[C_{\mathrm{NN}}+C_{\mathrm{EE}} \pm \sqrt{\left(C_{\mathrm{NN}}-C_{\mathrm{EE}}\right)^2+4 C_{\mathrm{NE}}^2}\right] $ | (2) |
理想情况下,地震数据没有噪音干扰,则协方差矩阵C有且仅有1个特征值,该特征值对应的特征向量就是P波水平偏振方向。实际情况中,地震数据通常存在噪音干扰,协方差矩阵C存在2个特征值,分别对应地震记录中P波偏振运动的线性程度和数据的噪音水平(Niu et al,2011)。因此,地震台站的后方位角可由最大特征值所对应的特征向量求得,其形式如下
| $ \theta_{\mathrm{a}}=\cot ^{-1} \frac{C_{\mathrm{EE}}-C_{\mathrm{NN}}+\sqrt{\left(C_{\mathrm{NN}}-C_{\mathrm{EE}}\right)^2+4 C_{\mathrm{NE}}^2}}{2 C_{\mathrm{NE}}} $ | (3) |
该方法被称为主成分分析法(PCA,principal component analysis),它不仅可用在方位角估算中,在单台地震预警工作中的应用也十分广泛(Lockman et al,2005;Noda et al,2012)。
为了更加准确地估算台站方位角偏差φ,还可利用多事件信噪比加权叠加法(Min-T,minimizing transverse energy method)对台站方位角进行约束(Niu et al,2011)。将每个地震事件的水平分量按指定方位角旋转至切向、径向分量,然后计算所有事件切向分量中P波能量加权之和
| $ E_T(\varphi)=\frac{\sum_{i=1}^N \omega_i E_T^i(\varphi)}{\sum_{i=1}^N \omega_i} $ | (4) |
其中,
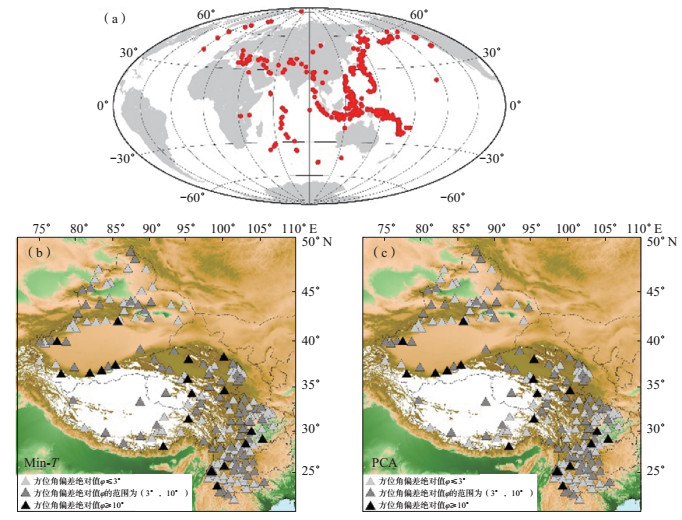
利用2019年1月至2020年12月西藏、云南、四川、青海、新疆等的211个宽频带地震台站记录的507个MS≥5.5地震事件开展方位角研究(图 2)。为排除地壳各向异性对研究结果的影响,通常选取震中距30°—90°范围内的远震波形参与台站方位角的计算(Niu et al,2011)。Fontaine等(2009)利用P波极化方法研究澳大利亚和塔希提岛上地幔各向异性时发现,可以适当扩展地震事件的震中距范围以提升台站方位角覆盖。Wang等(2016)研究表明,当震中距为5°时,计算出的后方位角偏差约2°,这极大地提升了台站的方位角覆盖,可以有效减小地震各向异性和倾斜界面的干扰。因此选取震中距5°—90°的地震事件参与计算。
|
图 2 研究区域台站、地震事件震中分布 (a)地震事件分布;(b)利用Min-T方法获得的方位角偏差;(c)利用PCA方法估算得到的方位角偏差浅灰色、深灰色、黑色实心三角表示不同方位角偏差的台站;红色圆圈代表使用的地震事件 Fig.2 Map shows thelocation of permanent seismic stations and earthquakes. |
考虑到某些台站地震计可能进行过移动和更换,故计算方位角偏差φ随时间的变化和波形互相关值(垂向和径向)的变化,并记录互相关数值出现反转的情况,判断可能的地震计方位角校正活动,分段统计地震计平均方位角偏差(Niu et al,2011;Wang et al,2016;Doran et al,2017)。主要处理步骤如下:①根据一维Iasp91模型计算直达P波的理论到时,利用零相位带通滤波器进行5—50 s长周期滤波处理,消除介质不均匀散射效应对结果的影响;②截取P波数据;③为保证地震计方位角估算的准确性,参与计算的每个事件需均满足2个水平分量信噪比0.5×SNR_((BHN+BHE))≥2.5、特征值λmin / λmax<0.2、径向分量和垂向分量间相关系数>0.8的条件;④每个台站至少有10个地震事件参与计算,以保证方位角计算结果的可靠性;⑤通过地震事件方位角偏差φ随时间的变化判断地震计可能的校正、变动情况,分段计算地震计变动前后平均方位角偏差。
3 结果分析使用2019—2020年的地震数据,利用P波质点运动的PCA、Min-T方法,对位于中国西北、西南地区的211个地震台站进行方位角计算,由PCA、Min-T方法所得计算结果的高度一致性表明,P波质点运动分析算法准确性、可靠性较高。计算结果显示,211个地震台站中53%的台站方位角偏差绝对值小于3°,运维情况极佳(图 2)。
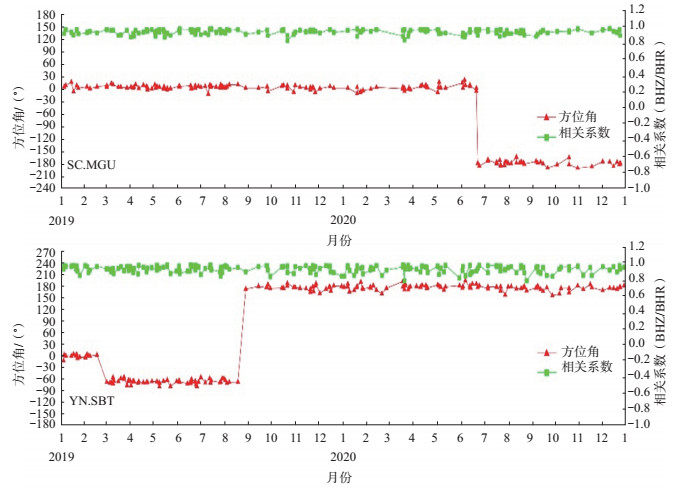
由Min-T方法得到的结果为多个事件的加权平均,仅反映了台站一段时间内方位角偏转的平均水平。利用PCA方法可计算单个事件的台站方位角,通过绘制台站方位角随时间变化的序列图,可有效反映台站方位角的变化情况。以SC.MGU台站为例[图 3(a)],在2020年6月中旬前,由PCA方法估算出的方位角偏差为1.54°±3.77°,而从6月中旬开始,地震计的方位角偏差突然增大至-178.67°±4.07°。四川地震台网运维日志显示,2020年6月23日SC.MGU台站地震计更换,核查后发现方位角偏差突然增大的原因是地震计安装过程中指北标识装反向。由于通过方位角变化时间序列图推测出的地震计更换的时间段与运维日志记录基本一致,故推测YN.SBT台站的方位角变化原因可能与SC.MGU台站类似[图 3(b)]。因此建议在台站运维过程中,每次更换或移动地震计后应收集一段时间的地震数据以对仪器方位角情况进行检验。
|
图 3 单地震PCA方法估算SC.MGU(a)、YN.SBT(b)台站地震计方位角偏差 Fig.3 Themisorientation calculated by PCA method for SC.MGU and YN.SBT stations |
在对结果统计的分析中发现,一些台站地震计存在NS、EW分量极性反转等问题,通过旋转分量,可使方位角偏差维持在-45°—45°之间(Niu et al,2011)。将计算得到的地震计方位角偏转角度绝对值分为3类进行统计,分别是φ≤3°、3°<φ<10°、φ≥10°,如此分类有助于清晰地了解我国西北、西南地区固定地震台站的运行状况。表 1给出了方位角偏差绝对值大于10°或需要进行特殊处理的台站信息。通常认为,偏差小于3°的台站维护状况良好,基本不存在地震计方位偏转的情况;3°—10°的台站方位角偏差可能是地震计本身的方向偏转叠加近台结构的各向异性、倾斜界面及一些其他波形传播影响的综合体现;若方位角偏差绝对值大于10°,则大概率是地震计本身的方向存在转向问题(Schulte-Pelkum et al,2001;Davis,2003;Wang et al,2016;Ojo et al,2019)。统计结果显示,2019—2020年我国西北、西南地区固定台站地震计保持着较高的方位准确率,53%的台站方位角偏差绝对值保持在3°以内,39%的台站维持在3°—10°,9%的台站达到10°以上,其中,5%的台站超过20°(图 2)。对于存在问题的台站,通过采取制作永久方位标志、重新安装地震计等措施可进一步提高地震监测数据的质量。
| 表 1 问题台站方位角 Table 1 Misoriented stations |
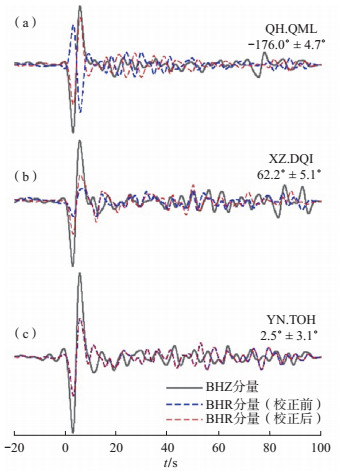
利用P波质点运动方法,对地震计的2个水平分量进行方位角估算。理论上,垂向、径向分量应具有相似的波形,波形应具有相同的相位。通过校正前后垂向、径向分量波形的变化,可以辅助判断台站是否存在方位角偏转问题及计算出的方位角校正数值是否可靠(Ojo et al,2019;Zeng et al,2020)。选取QH.QML、XZ.DQI、YN.TOH等3个台站,利用2019年4月6日南桑维奇群岛MW 6.3地震事件,绘制校正前后的径向分量,并与垂向分量进行对比(图 4)。由图 4可见,QH.QML台站方位角偏转达到-176°±4.7°,校正前径向、垂向分量极性相反,校正后分量极性一致;XZ.DQI台站方位角偏差62.2°±5.1°,校正后径向分量波形与垂向分量波形间的相关性明显增大;YN.TOH台站基本不存在方位角偏转问题(2.5°±3.1°),校正前后径向分量波形一致性极高,在数据使用过程中,无需进行方位角校正。
|
图 4 垂向分量与波形校正前、后径向分量的对比 (a)QH.QML台;(b)XZ.DQI台;(c)YN.TOH台 Fig.4 Comparison of vertical componentand radial componentwaveforms before and after azimuth correction |
自2012年以来,中国地震局开展了全国范围内的测震台站仪器方位角普查和校正工作,使用陀螺寻北仪查找台站仪器方位角及极性,台站方位角偏差问题得到了有效解决(李少睿等,2014)。我们使用2019—2020年地震数据,利用P波质点运动方法,对我国西北、西南地区211个地震台站的方位角进行了检查。利用PCA、Min-T方法的估算结果显示,约91%的台站方位角偏差绝对值在10°以内,9%的台站达到10°以上,其中,5%的台站超过20°。建立台站方位角随时间变化的序列图,可有效反映台站方位角的变化情况,对出现问题的台站及时校正,保证地震数据的稳定性和可靠性。
陈兵, 王庆良, 张四新, 等. 青藏块体北部构造形变与玉门5.9级地震[J]. 大地测量与地球动力学, 2003, 23(2): 23-28. |
陈继锋, 李亮, 李少睿, 等. 甘肃省测震台网地震台站地震计方位角检验与校正[J]. 地震工程学报, 2016, 38(3): 460-465. |
陈家樑, 戴丽金, 张宝剑. 利用P波质点运动检测福建台网地震计方位角[J]. 华北地震科学, 2021, 39(3): 45-50. |
李少睿, 赵建和, 王党席, 等. 全国测震台站仪器方位角普查校正[J]. 地震地磁观测与研究, 2014, 35(1/2): 224-230. |
李伟, 丁志峰, 孙伟家. 利用地震光照成像法研究青藏高原东南缘岩石圈间断面结构及其动力学意义[J]. 地震学报, 2019, 41(5): 549-568. |
王婷, 薛梅. 阿留申群岛地震台站方位角变化及其对横波分裂的影响[J]. 地震学报, 2020, 42(2): 187-195. |
魏贵春, 姚运生, 张丽芬, 等. 方位角对地方震震级测定的影响[J]. 地震学报, 2017, 39(6): 880-890. |
许英才, 曾宪伟, 许文俊, 等. 基于台阵的青藏高原东北缘海原-六盘山断裂带及邻区地壳结构研究[J]. 中国地震, 2018, 34(3): 484-497. |
中国地震局. DB/T 22-2020地震观测仪器进网技术要求地震仪[S]. 2020.
|
Baker G E, Stevens J L. Backazimuth estimation reliability using surface wave polarization[J]. Geophysical Research Letters, 2004, 31(9): L09-611. |
Davis P M. Azimuthal variation in seismic anisotropy of the southern California uppermost mantle[J]. Journal of Geophysical Research: Solid Earth, 2003, 108(B1): 2 052. |
Doran A K, Laske G. Ocean-bottom seismometer instrument orientations via automated Rayleigh-wave arrival-angle measurements[J]. Bulletin of the Seismological Society of America, 2017, 107(2): 691-708. |
Ekström G, Busby R W. Measurements of seismometer orientation at USArray transportable array and backbone stations[J]. Seismological Research Letters, 2008, 79(4): 554-561. |
Fontaine F R, Barruol G, Kennett B L N, et al. Upper mantle anisotropy beneath Australia and Tahiti from P wave polarization: implications for real-time earthquake location[J]. Journal of Geophysical Research: Solid Earth, 2009, 114(B3): B03306. |
Jurkevics A. Polarization analysis of three-component array data[J]. Bulletin of the Seismological Society of America, 1988, 78(5): 1 725-1 743. |
Laske G. Global observation of off-great-circle propagation of long-period surface waves[J]. Geophysical Journal International, 1995, 123(1): 245-259. |
Lockman A B, Allen R M. Single-station earthquake characterization for early warning[J]. Bulletin of the Seismological Society of America, 2005, 95(6): 2 029-2 039. |
Niu F L, Li J. Component azimuths of the CEArray stations estimated from P-wave particle motion[J]. Earthquake Science, 2011, 24(1): 3-13. |
Noda S, Yamamoto S, Sato S, et al. Improvement of back-azimuth estimation in real-time by using a single station record[J]. Earth, Planets and Space, 2012, 64(3): 305-308. |
Ojo A O, Zhao L, Wang X. Estimations of sensor misorientation for broadband seismic stations in and around Africa[J]. Seismological Research Letters, 2019, 90(6): 2 188-2 204. |
Ringler A T, Hutt C R, Persefield K, et al. Seismic station installation orientation errors at ANSS and IRIS/USGS stations[J]. Seismological Research Letters, 2013, 84(6): 926-931. |
Rueda J, Mezcua J. Orientation analysis of the spanish broadband national network using Rayleigh-wave polarization[J]. Seismological Research Letters, 2015, 86(3): 929-940. |
Schulte-Pelkum V, Masters G, Shearer P M. Upper mantle anisotropy from long-period P polarization[J]. Journal of Geophysical Research: Solid Earth, 2001, 106(B10): 21 917-21 934. |
Selby N D. Association of Rayleigh waves using backazimuth measurements: application to test ban verification[J]. Bulletin of the Seismological Society of America, 2001, 91(3): 580-593. |
Stachnik J C, Sheehan A F, Zietlow D W, et al. Determination of new Zealand ocean bottom seismometer orientation via Rayleigh-wave polarization[J]. Seismological Research Letters, 2012, 83(4): 704-713. |
Wang X, Chen Q F, Li J, et al. Seismic sensor misorientation measurement using P-wave particle motion: an application to the NECsaids array[J]. Seismological Research Letters, 2016, 87(4): 901-911. |
Zeng S J, Zheng Y, Niu F L, et al. Measurements of seismometer orientation of the first phase CHINArray and their implications on vector-recording-based seismic studies[J]. Bulletin of the Seismological Society of America, 2020, 111(1): 36-49. DOI:10.1785/0120200129 |
Zha Y, Webb S C, Menke W. Determining the orientations of ocean bottom seismometers using ambient noise correlation[J]. Geophysical Research Letters, 2013, 40(14): 3 585-3 590. |
 2023, Vol. 44
2023, Vol. 44

