0 引言

重力场是地球基本场之一，其时空变化是地球动力学的重要组成部分，对研究地震孕育过程、了解深部地壳环境变化具有重要作用(褚庆忠等，2014)。通过对地球重力场的观测，可研究地球质量分布、地球运动及自身变形规律。而局部地壳的应变、地震的形成过程、地下流体的运动，均可能引起地面重力场发生非潮汐变化。利用重力仪可以观测地球固体潮变化，地震台站目前广泛应用PET/gPhone型重力仪(曾华霖，1999)进行重力监测，重力观测记录的主要成分即为固体地球潮汐分量，采用Venedikov调和分析方法(下文简称VAV方法)进行固体潮分析，即可获得非潮汐结果(田桂娥等，2005)。Venedikov调和分析方法是在原有最小二乘法基础上发展的固体潮分析软件，目前应用较广(Ducarme et al，2004)。

2018年5月28日吉林省松原市宁江区发生M_S 5.7地震，本文基于波形初动、延迟时间、同震形态、最大形变幅度以及同震持续时间等，分析黑龙江省漠河、牡丹江地震台重力监测数据的同震响应特征，并利用Venedikov调和分析方法，分析牡丹江地震台(下文简称牡丹江台)重力固体潮非潮汐变化，捕捉其与地震的对应关系。

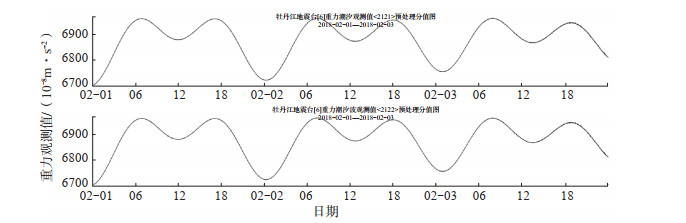
1 黑龙江省重力监测台站概况

黑龙江省目前设有牡丹江和漠河2个重力监测台站，其中牡丹江台采用PET型重力仪、漠河台采用gPhone型重力仪进行观测。2套重力仪均为美国劳雷公司生产的金属弹簧相对重力仪，无需调整量程，秒采样，可长期观测，仪器灵敏度较高，数据质量稳定、可靠，对全球6.0级左右地震均有较明显的同震响应。以2个台站2018年2月1日—3日的连续重力观测数据为例，分析重力固体潮特征，结果见图 1，由图可见，重力记录固体潮形态清晰、完整，曲线光滑，日动态呈现“双峰双谷”的周期性变化。

2 黑龙江省重力监测的同震响应特征分析

北京时间2018年5月28日1时50分，在吉林省松原市宁江区发生M_S 5.7地震，震源深度13 km。黑龙江省牡丹江和漠河台2套重力仪均记录到此次地震，其中牡丹江台PET重力仪震中距约392 km，漠河台gPhone重力仪震中距约927 km，地震波形记录曲线见图 2。由图 2(a)可见，此次地震发生后1 min，即1时51分，牡丹江台重力观测曲线出现同震脉冲，无阶跃，波的初动方向向下，同震响应最大变化幅度为25 035.05×10^-8 cm/s²，持续时间约19 min。由图 2(b)可见，此次地震发生后2 min，即1时52分，漠河台重力仪秒值观测曲线出现同震响应，波的初动方向向下，同震响应观测曲线表现形态为脉冲，最大变化幅度为5 928.91×10^-8 cm/s²，持续时间约28 min。

脉冲是由连续定点形变观测到的地震传播到地面的震动信号的表现形式。地震波远距离传播形成面波，当面波的频率与形变观测仪器自振频率接近时会产生脉冲的共振现象。说明重力仪的自振周期与地震波的优势周期相近(郭明瑞等，2013)。

基于地震波的初动方向、延迟时间、同震响应变化最大振幅及持续时间，对比分析牡丹江和漠河台重力数据在此次松原地震中的同震响应特征。

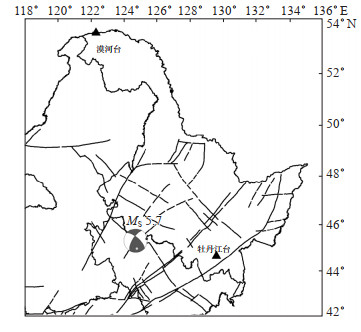
2.1 地震波的初动方向

黑龙江牡丹江、漠河台与2018年吉林松原M_S 5.7地震的相对位置分布见图 3，图中示出此次地震的震源机制解。由重力仪波形记录曲线(图 2)可知，牡丹江台和漠河台记录的重力波形曲线显示P波初动方向均向下。同时，吉林松原M_S 5.7地震的震源机制解(图 3中震源球)显示破裂类型为走滑型，其中牡丹江台P波初动向下记录清晰，而漠河台因震中距较远，P波初动记录不清晰。综上可以认为，PET和gPhone型重力仪记录的地震波信息频段与地震仪记录较接近，表明重力记录波形初动方向比较可靠。

2.2 地震波传播的延迟时间

地震波在岩石中的传播时间与其传播距离成正比，延迟时间长短一般可以反映震中距的远近(杨婕等，2010)。漠河台与此次吉林松原地震震中相距更远，故牡丹江台重力仪记录的同震响应波的延迟时间为1 min，而漠河台重力仪记录的同震形变波延迟时间较长，为2 min。

2.3 同震响应最大振幅

黑龙江省牡丹江和漠河台重力仪记录的此次吉林松原地震波形曲线显示，同震响应形态主要表现为脉冲震荡，且牡丹江台PET型重力仪记录的最大同震响应变化幅度较大，主要是因为该台震中距较小，地震波在传播过程中能量衰减较小，故同震响应变化幅度较大。当然，地震波传播路径及地下介质结构的差异也会影响地震波能量的衰减程度，从而导致记录的最大同震响应变化幅度也会不同(林俊等，2017)。

2.4 同震响应持续时间

同震响应持续时间与观测仪器的分辨率有关，分辨率越高，对微小变化的反应越灵敏。据重力记录观测曲线(图 2)，牡丹江台同震响应持续时间约19 min，漠河台同震响应持续时间约28 min。这是因为，漠河台gPhone重力仪分辨率更高，故同震响应持续时间较长，当然，也可能与地下介质结构相关。

3 牡丹江台重力固体潮非潮汐变化

基于以上同震响应特征，认为黑龙江省重力测项观测到2018年吉林松原M_S 5.7地震触发记录。以牡丹江台重力数据为例，采用Venedikov调和分析方法，分析吉林松原M_S 5.7地震发生前后重力固体潮非潮汐变化。

(1) 方法原理。据Venedikov调和分析方法，t时刻的重力观测值y(t)为

$ y(t)=s(t)+d(t)+p(t)+\varepsilon(t) $

(1)

式中，s(t)为重力潮汐，d(t)为漂移，p(t)为非潮汐变化影响，ε(t)为观测噪声。

采用逐步回归模型对漂移量d(t)进行拟合，将观测数据分为T组，每组数据长度为24小时，每组漂移值保持稳定且相互独立。采用低阶多项式，对组内数据进行漂移拟合，设第T个时间窗内数据的漂移为d(T + t)，则有

$d(T+t)=\sum _{i=0}^k Z_j(T) t^j=p(t) a(t) $

(2)

式中，Z_j(T)为未知拟合系数，k为多项式阶数。

采用交叉回归模型，求解非潮汐信号对重力观测的影响。设t时刻非潮汐信号为q(t)，其对重力观测的影响为p(t)，表示为

$ p(t)=\sum _{i=1}^k a_i q(t-i) $

(3)

式中，a_i为回归系数，i为交叉回归次数。

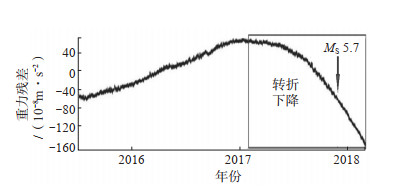
(2) 重力非潮汐变化。选取牡丹江台PET型相对重力仪2016年1月至2018年8月的连续观测数据，采用Venedikov调和分析方法，进行仪器零漂和气压改正，得到该台重力数据非潮汐变化时间序列，结果见图 4。由图 4可见，2017年8月起，牡丹江台固体潮残差值呈下降趋势变化，至2018年5月28日吉林松原M_S 5.7地震发生，平均每月下降约15×10^-8 cm/s²，总降幅约158×10^-8 cm/s²，震后仍呈下降趋势，总降幅约73×10^-8 cm/s²，平均每月下降约25×10^-8 cm/s²，可见该台重力固体潮非潮汐变化并非只受到此次松原M_S 5.7地震触发作用影响。

为此，进行干扰和故障排查。从据现场调查可知：该台站周边10 km范围内无大型水库、河流、大型抽水站等干扰源；距重力监测站直线距离约30 m的乡村公路过往车辆未对重力观测造成显著影响；观测山洞SE方向约1 km处新建居民区施工场地对重力观测影响不大。牡丹江台设有气温、气压和降雨气象三要素辅助观测测项。由2016年—2018年8月三要素原始观测曲线(图 5)可见，气压、温度、降雨量均呈以年为单位的季节性变化规律。

检查PET重力仪发现，UPS指示灯显示正常，仪器内温恒定。牡丹江台PET重力仪2007年安装，仪器元件存在老化问题，灵敏度可能有所下降。因此，重力仪虽然能记录到此次吉林松原M_S 5.7地震前后的非潮汐变化，但仪器灵敏度下降导致仪器测量精度的变化，会对记录到的非潮汐变化也有一定影响。

4 讨论与认识

黑龙江省牡丹江台和漠河台重力仪自2016年起，近3年时间内整体观测质量稳定，并能记录到大多数地震的同震响应。针对此次吉林松原M_S 5.7地震，2套重力仪记录的同震响应形态基本相同，均为脉冲变化，且P波初动方向与地震仪记录一致，地震波信息频段与地震仪记录也较接近。2台重力仪同震响应延迟时间、最大同震响应变化幅度、持续时间不同，与震中距、地震波传播路径、地质结构及仪器分辨率等有一定关系。

牡丹江台和漠河台重力仪均能记录到清晰固体潮变化。在此次吉林松原M_S 5.7地震发生前10个月内，牡丹江台重力非潮汐呈持续性下降变化，月均变化速度为15×10^-8 cm/s²，累计变化158×10^-8 cm/s²，震后下降变化仍在持续。由于地震孕育和地下物质运移过程是缓慢的，难以在短时间内形成较大的重力变化。一般而言，值得重点关注和跟踪的非潮汐变化，其月均变化幅度一般在(5—10)×10^-8 cm/s²。

因此，此次牡丹江台记录的连续重力非潮汐变化，在无明显垂直形变情况下，下降速度过快，除与吉林松原M_S 5.7地震导致的地球物理场变化有关，可能也与仪器灵敏度下降有一定关系，具体相关性有待进一步研究。

文中使用的重力数据来源于中国地震台网中心及台站资料，湖北省地震局申重阳研究员和韦进副研究员对论文撰写提出建议，在此一并表示感谢。